Напомню, в первой части речь шла о вычислении простых импликант (конъюнкций) для циклических поведений без параллелизма, выбора и кратных сигналов по трем точкам (состояниям).

Задача состояла в том, чтобы импликанта покрыла точку 2 (то есть была равна 1 на этом состоянии) и не выходила за пределы обозначенные точками 1 и 3… При этом положение левой границы импликанты (левее точки 2) безразлично. Правая граница (правее точки 2) должна быть максимально сдвинута вправо. Невозможность вычисления импликанты означает наличие CSC конфликта. То есть существует непрерывная последовательность событий (но не все поведение целиком), в которой каждый сигнал переключается четное число раз.
Приступим теперь к вычислению минимальной логической функции (ДНФ) для сигнала x.
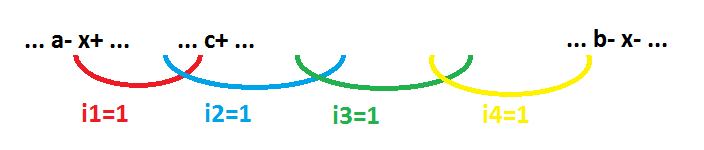
Построить функцию для сигнала x это значит покрыть импликантами все состояния, где функция сигнала x равна 1. В данном примере это последовательность состояний, начинающаяся сразу после события a- и заканчивающаяся непосредственно перед событием b-. Импликанты обозначены цветными дугами. При этом ни одна импликанта не должна покрывать состояние, на котором функция сигнала x равна 0. Напомню, что под импликантой мы понимаем набор состояний где она равна 1. В данном примере получится неинвертирующая функция (И-ИЛИ). Если перекрывать импликантами пространство от "-" события до "+" события (по направлению разворачивания процесса), то получим инвертирующую функцию (И-ИЛИ-НЕ). Еще одно важное замечание. Поскольку логическая функция вычисляется для элемента самосинхронной схемы, соседние импликанты должны пересекаться, то есть иметь хотя бы одно общее состояние.
Алгоритм вычисления минимальной функции выглядит следующим образом. При задании места расположения вычисляемой импликанты в качестве точки 1 всегда будем использовать точку, находящуюся справа от события a- (на рисунке). А в качестве точки 3 всегда будем использовать точку, находящуюся слева от события b- (на рисунке). Импликанты будем вычислять последовательно друг за другом в направлении от события x+ до события x-. Сначала красную, потом синюю, потом зеленую и так далее (на рисунке). Это обусловлено используемым алгоритмом вычисления простой импликанты.
Шаг 1. В качестве точки 2 выберем точку, расположенную слева от события x+ (на рисунке).
Шаг 2. Вычислим по заданным трем точкам импликанту. Полученная импликанта входит в итоговую запись функции.
Замечание. Если получено несколько альтернативных импликант, то нужно рассмотреть каждый вариант включения в итоговую запись функции одной из альтернативных импликант. Соответственно для каждого варианта вычисления должны быть продолжены отдельно.
Шаг 3. Рассмотрим правую границу только что вычисленной импликанты. На рисунке это событие c+ (для первой вычисленной импликанты). Если правая граница импликанты является непосредственной причиной события x-, это значит, что вычисление функции закончено, выходим из алгоритма.
Шаг 4. В качестве точки 2 выберем точку расположенную слева от правой границы последней вычисленной импликанты. Переходим к шагу 2.
Этот алгоритм исходит из того, что вид минимальной функции не определен. Но для модели, рассматриваемой в данный момент, минимальная функция любого сигнала может быть записана следующим образом:
1)
— это импликанта, состоящая из одной или более переменных. — это возможно пустое множество импликант, состоящих из одной переменной. — это импликанта из 2 переменных, наличие которой в минимальной форме не обязательно. Все переменные, кроме x, могут входить в формулу как в прямом, так и в инверсном виде, в зависимости от расстановки знаков соответствующих событий. Все переменные входят в формулу в качестве аргументов строго по одному разу.
Действительно, рассмотрим возможные варианты расположения первой вычисляемой импликанты. Таких вариантов два. Первый, когда правая граница импликанты является причиной события x-:

В этом случае импликанта покрывает все состояния, на которых функция x равна 1. Функция выглядит так: x=a*b*c. В дальнейшем для обозначения импликанты будем использовать только ее границы. В данном примере это a+ и c- (соответственно левая и правая границы). Все знаки событий (кроме переключений сигнала x) носят условный характер и могут быть заменены на противоположный. Они призваны лишь различать события с одинаковым именем.
Второй вариант расположения импликанты — правая граница импликанты не является непосредственной причиной события x-:

В этом случае сигнал f, "-" переключение которого является непосредственной причиной события x-, может располагаться тремя различными способами.
Первый вариант расположения события f+ — между событиями x- и a+ (по ходу развертывания процесса):

В этом случае вторая импликанта не может состоять из одной переменной. А вот импликанта f*x покрывает все оставшиеся непокрытыми состояния, на которых функция x равна 1. Такому расположению события f+ соответствует формула x=a*b*c+f*x.
Второй вариант расположения события f+ — между событиями x+ и c-:
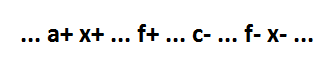
В этом случае вторая и последняя импликанта состоит из одной переменной f, что соответствует формуле x=a*b*c+f.
Третий вариант расположения события f+ — между событиями c- и f-:
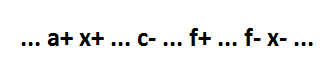
В этом случае, как и в предыдущем, импликанта f обязательно должна войти в состав минимальной функции. Только в этом случае этой импликанты не достаточно для завершения построения функции. Рассмотрим некое событие g-, расположенное между событиями f+ и f-. Такое событие обязательно должно быть, иначе это означало бы CSC конфликт.
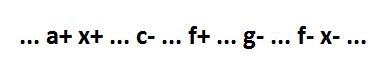
Для события g+ 4 варианта расположения. Первый вариант расположения события g+ — между событиями x+ и c-:
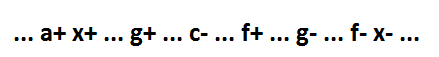
В этом случае импликанты g достаточно для завершения построения минимальной функции, которая выглядит так x=a*b*c+f+g.
Если не существует события g+, расположенного между событиями x+ и c-, рассмотрим второй вариант расположения события g+ — между событиями x- и a+:

В этом случае не существует третьей импликанты, состоящей из одной переменной, иначе это был бы первый вариант расположения события g+. А вот импликанты g*x достаточно для завершения вычисления минимальной функции. Формула выглядит так: x=a*b*c+f+g*x.
Третий вариант. Если для любого сигнала g событие g+ расположено между событиями f+ и f-. Это означает CSC конфликт.

Остается четвертый вариант. Событие g+ расположено между событиями c- и f+.
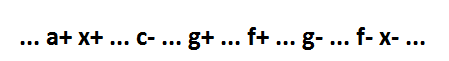
Так как нет таких сигналов g, которые удовлетворяли бы первому или второму вариантам расположения события g+, импликанта, состоящая из одной переменной g, обязательно должна войти в минимальную форму.
Далее рассмотрим какой-то сигнал h, переключение которого расположено между событиями g+ и f+.
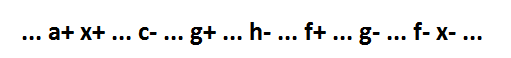
И рассмотрим варианты расположения события h+ также, как это делали для события g+. В конце концов мы либо обнаружим CSC конфликт, либо получим формулу 1).
Что дает эта формула? Первое. Сигналы f, g, h, i из формулы образуют цепочку перехватов и по сути являются импликантой. Таким образом вычисление минимальной функции сводится к нахождению двух импликант. Только задание условий для поиска несколько отличается от того, что было сказано выше. Сложность алгоритма вычисления в пределе квадратичная относительно количества сигналов. Но квадратичная составляющая имеет пренебрежимо малый вес. Поэтому можно говорить о линейной сложности. Ну и в добавок алгоритм практически не требует памяти.
Второй момент. Такая запись минимальной функции позволяет делать декомпозицию до сколь угодно малых элементов, не нарушая самосинхронности. Рассмотрим функцию x=a*b+f+g+h*x. Поведение ее выглядит так:
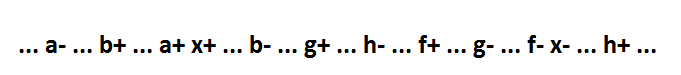
Такую функцию полностью декомпозировать нельзя. Этот недостаток исправляется добавлением сигнала y:

Теперь функции выглядят так: x=(f+g+h)*y, y=a*b+x. Для сохранения самосинхронности осталось заменить аргумент функции сигнала, причиной переключения которого являлось событие x-: x меняем на y.
Рассмотрим функцию x=a*b*c+f+g. Ее поведение:
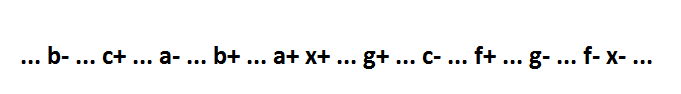
Для такой функции всегда можно без потери самосинхронности выделить в качестве отдельного элемента первую импликанту: y=a*b*c, x=y+g+f. Поведение с новым элементом будет таким:
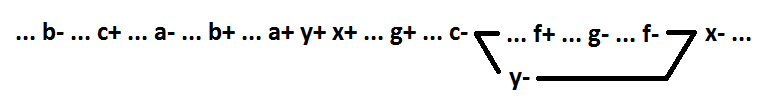
Забегая вперед, пришлось использовать параллелизм. Подробнее об этом дальше. Осталось рассмотреть функцию вида x=a*b*c*d. Ее поведение:
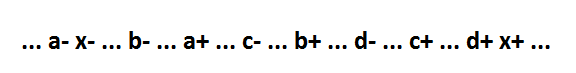
В такой функции всегда можно выделить в качестве отдельного элемента без потери самосинхронности первые переменные (например a, b, c): y=a*b*c, x=y*d. Поведение с новым элементом:
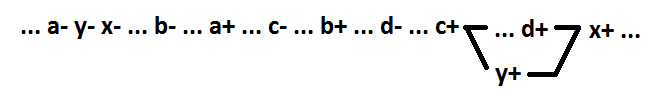
Используя эти три преобразования можно дробить логические элементы до необходимого уровня.
Остается вопрос: насколько все это имеет практическую ценность? Ведь пока рассматривается очень ограниченная модель. В дальнейшем я покажу, что для любого поведения, используя преобразования линейной сложности (добавление новых сигналов), вычисление логической функции для любого сигнала можно свести к поиску двух импликант. И полученную функцию можно будет дробить до необходимого уровня. Продолжение следует.

Задача состояла в том, чтобы импликанта покрыла точку 2 (то есть была равна 1 на этом состоянии) и не выходила за пределы обозначенные точками 1 и 3… При этом положение левой границы импликанты (левее точки 2) безразлично. Правая граница (правее точки 2) должна быть максимально сдвинута вправо. Невозможность вычисления импликанты означает наличие CSC конфликта. То есть существует непрерывная последовательность событий (но не все поведение целиком), в которой каждый сигнал переключается четное число раз.
Приступим теперь к вычислению минимальной логической функции (ДНФ) для сигнала x.

Построить функцию для сигнала x это значит покрыть импликантами все состояния, где функция сигнала x равна 1. В данном примере это последовательность состояний, начинающаяся сразу после события a- и заканчивающаяся непосредственно перед событием b-. Импликанты обозначены цветными дугами. При этом ни одна импликанта не должна покрывать состояние, на котором функция сигнала x равна 0. Напомню, что под импликантой мы понимаем набор состояний где она равна 1. В данном примере получится неинвертирующая функция (И-ИЛИ). Если перекрывать импликантами пространство от "-" события до "+" события (по направлению разворачивания процесса), то получим инвертирующую функцию (И-ИЛИ-НЕ). Еще одно важное замечание. Поскольку логическая функция вычисляется для элемента самосинхронной схемы, соседние импликанты должны пересекаться, то есть иметь хотя бы одно общее состояние.
Алгоритм вычисления минимальной функции выглядит следующим образом. При задании места расположения вычисляемой импликанты в качестве точки 1 всегда будем использовать точку, находящуюся справа от события a- (на рисунке). А в качестве точки 3 всегда будем использовать точку, находящуюся слева от события b- (на рисунке). Импликанты будем вычислять последовательно друг за другом в направлении от события x+ до события x-. Сначала красную, потом синюю, потом зеленую и так далее (на рисунке). Это обусловлено используемым алгоритмом вычисления простой импликанты.
Шаг 1. В качестве точки 2 выберем точку, расположенную слева от события x+ (на рисунке).
Шаг 2. Вычислим по заданным трем точкам импликанту. Полученная импликанта входит в итоговую запись функции.
Замечание. Если получено несколько альтернативных импликант, то нужно рассмотреть каждый вариант включения в итоговую запись функции одной из альтернативных импликант. Соответственно для каждого варианта вычисления должны быть продолжены отдельно.
Шаг 3. Рассмотрим правую границу только что вычисленной импликанты. На рисунке это событие c+ (для первой вычисленной импликанты). Если правая граница импликанты является непосредственной причиной события x-, это значит, что вычисление функции закончено, выходим из алгоритма.
Шаг 4. В качестве точки 2 выберем точку расположенную слева от правой границы последней вычисленной импликанты. Переходим к шагу 2.
Этот алгоритм исходит из того, что вид минимальной функции не определен. Но для модели, рассматриваемой в данный момент, минимальная функция любого сигнала может быть записана следующим образом:
1)
— это импликанта, состоящая из одной или более переменных. — это возможно пустое множество импликант, состоящих из одной переменной. — это импликанта из 2 переменных, наличие которой в минимальной форме не обязательно. Все переменные, кроме x, могут входить в формулу как в прямом, так и в инверсном виде, в зависимости от расстановки знаков соответствующих событий. Все переменные входят в формулу в качестве аргументов строго по одному разу.
Действительно, рассмотрим возможные варианты расположения первой вычисляемой импликанты. Таких вариантов два. Первый, когда правая граница импликанты является причиной события x-:

В этом случае импликанта покрывает все состояния, на которых функция x равна 1. Функция выглядит так: x=a*b*c. В дальнейшем для обозначения импликанты будем использовать только ее границы. В данном примере это a+ и c- (соответственно левая и правая границы). Все знаки событий (кроме переключений сигнала x) носят условный характер и могут быть заменены на противоположный. Они призваны лишь различать события с одинаковым именем.
Второй вариант расположения импликанты — правая граница импликанты не является непосредственной причиной события x-:

В этом случае сигнал f, "-" переключение которого является непосредственной причиной события x-, может располагаться тремя различными способами.
Первый вариант расположения события f+ — между событиями x- и a+ (по ходу развертывания процесса):

В этом случае вторая импликанта не может состоять из одной переменной. А вот импликанта f*x покрывает все оставшиеся непокрытыми состояния, на которых функция x равна 1. Такому расположению события f+ соответствует формула x=a*b*c+f*x.
Второй вариант расположения события f+ — между событиями x+ и c-:
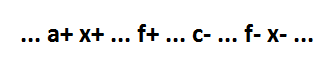
В этом случае вторая и последняя импликанта состоит из одной переменной f, что соответствует формуле x=a*b*c+f.
Третий вариант расположения события f+ — между событиями c- и f-:
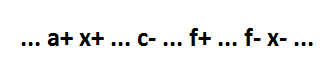
В этом случае, как и в предыдущем, импликанта f обязательно должна войти в состав минимальной функции. Только в этом случае этой импликанты не достаточно для завершения построения функции. Рассмотрим некое событие g-, расположенное между событиями f+ и f-. Такое событие обязательно должно быть, иначе это означало бы CSC конфликт.
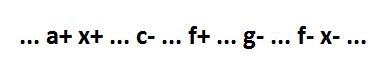
Для события g+ 4 варианта расположения. Первый вариант расположения события g+ — между событиями x+ и c-:
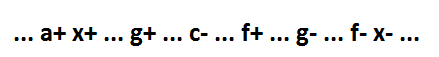
В этом случае импликанты g достаточно для завершения построения минимальной функции, которая выглядит так x=a*b*c+f+g.
Если не существует события g+, расположенного между событиями x+ и c-, рассмотрим второй вариант расположения события g+ — между событиями x- и a+:

В этом случае не существует третьей импликанты, состоящей из одной переменной, иначе это был бы первый вариант расположения события g+. А вот импликанты g*x достаточно для завершения вычисления минимальной функции. Формула выглядит так: x=a*b*c+f+g*x.
Третий вариант. Если для любого сигнала g событие g+ расположено между событиями f+ и f-. Это означает CSC конфликт.

Остается четвертый вариант. Событие g+ расположено между событиями c- и f+.
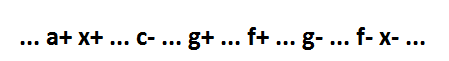
Так как нет таких сигналов g, которые удовлетворяли бы первому или второму вариантам расположения события g+, импликанта, состоящая из одной переменной g, обязательно должна войти в минимальную форму.
Далее рассмотрим какой-то сигнал h, переключение которого расположено между событиями g+ и f+.
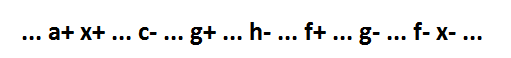
И рассмотрим варианты расположения события h+ также, как это делали для события g+. В конце концов мы либо обнаружим CSC конфликт, либо получим формулу 1).
Что дает эта формула? Первое. Сигналы f, g, h, i из формулы образуют цепочку перехватов и по сути являются импликантой. Таким образом вычисление минимальной функции сводится к нахождению двух импликант. Только задание условий для поиска несколько отличается от того, что было сказано выше. Сложность алгоритма вычисления в пределе квадратичная относительно количества сигналов. Но квадратичная составляющая имеет пренебрежимо малый вес. Поэтому можно говорить о линейной сложности. Ну и в добавок алгоритм практически не требует памяти.
Второй момент. Такая запись минимальной функции позволяет делать декомпозицию до сколь угодно малых элементов, не нарушая самосинхронности. Рассмотрим функцию x=a*b+f+g+h*x. Поведение ее выглядит так:
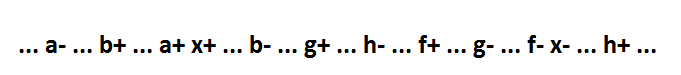
Такую функцию полностью декомпозировать нельзя. Этот недостаток исправляется добавлением сигнала y:

Теперь функции выглядят так: x=(f+g+h)*y, y=a*b+x. Для сохранения самосинхронности осталось заменить аргумент функции сигнала, причиной переключения которого являлось событие x-: x меняем на y.
Рассмотрим функцию x=a*b*c+f+g. Ее поведение:
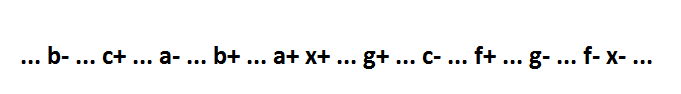
Для такой функции всегда можно без потери самосинхронности выделить в качестве отдельного элемента первую импликанту: y=a*b*c, x=y+g+f. Поведение с новым элементом будет таким:
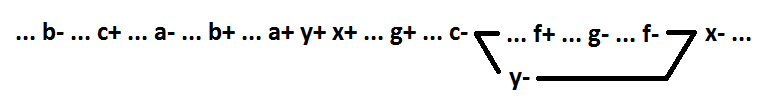
Забегая вперед, пришлось использовать параллелизм. Подробнее об этом дальше. Осталось рассмотреть функцию вида x=a*b*c*d. Ее поведение:
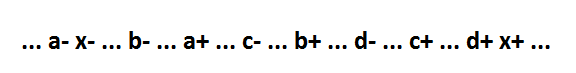
В такой функции всегда можно выделить в качестве отдельного элемента без потери самосинхронности первые переменные (например a, b, c): y=a*b*c, x=y*d. Поведение с новым элементом:
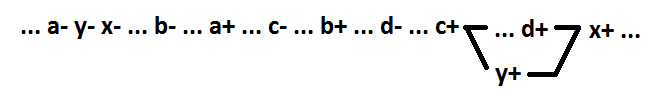
Используя эти три преобразования можно дробить логические элементы до необходимого уровня.
Остается вопрос: насколько все это имеет практическую ценность? Ведь пока рассматривается очень ограниченная модель. В дальнейшем я покажу, что для любого поведения, используя преобразования линейной сложности (добавление новых сигналов), вычисление логической функции для любого сигнала можно свести к поиску двух импликант. И полученную функцию можно будет дробить до необходимого уровня. Продолжение следует.

