tl;dr:

Учёные из Колумбийского университета во главе с Кеном Шепардом и Рафой Юсте заявили, что обошли столетнюю теорему отсчётов (теорема Найквиста — Шеннона, теорема дискретизации, в русскоязычной литературе — теорема Котельникова): 1, 2. Теперь фильтры защиты от наложения стали необязательными, ведь шум от наложения спектров можно восстановить после дискретизации. Звучит безумно? Да. Я предлагаю $1000 первому, кто докажет, что это не безумие. Чтобы получить награду, обязательно прочтите до конца.

«Фильтруй перед дискретизацией!»

Эта мантра насмерть вбита в головы поколений студентов-инженеров. Здесь под «дискретизацией» подразумевается преобразование непрерывной функции времени в серию дискретных значений. Такой процесс происходит везде, где компьютер оцифровывает сигнал из реального аналогового мира. «Фильтровать» — значит удалять из сигнала высокочастотные составляющие. Поскольку этот процесс происходит в аналоговом мире, то требует реального аналогового оборудования: цепей из резисторов, конденсаторов и усилителей. Создание такой цепи может стать утомительным и трудоёмким процессом, например, если на электронных микросхемах не хватает места. Научная группа Шепарда рассмотрела это ограничение в контексте устройства для записи сигналов от нервных клеток.

Теперь авторы заявляют, что изобрели «парадигму сбора данных, которая не требует фильтров для защиты от наложения для каждого канала, тем самым преодолевая ограничения масштабирования существующих систем». По сути они говорят, что вместо аппаратных цепей можно использовать программное обеспечение, которое работает на цифровой стороне уже после дискретизации. «Ещё одним преимуществом такого подхода к сбору данных является то, что все шаги обработки сигнала (разделение каналов и удаление) реализованы в цифровом виде», сказано в научной работе.

Если это правда, то стало бы важнейшим открытием. Оно не только опровергает общепринятое мнение, которого придерживались почти столетие. Ешё и куча аппаратуры становится ненужной. Фильтры для защиты от наложения повсеместно используются в электронном оборудовании. В вашем мобильнике несколько цифровых радиочипов и аналого-цифровой преобразователь звуковых сигналов, а между ними с полдюжины микросхем для фильтров для защиты от наложения. Если можно заменить все эти электронные компоненты несколькими строками кода, то производители с радостью сделают это. Так что это потенциально идея на миллиард долларов.

К сожалению, это большая ошибка. Я покажу, что эти документы не имеют ничего общего с теоремой дискретизации. Они не отменяют обработку. И не отменяют аналоговые фильтры перед оцифровкой. И даже близко не приближаются к лучшим системам по извлечению нейронных сигналов из шума.

Почему наложение — это плохо

[пропустите эту часть, если знаете ответ]

Дискретизация — важнейший этап сбора данных, когда непрерывный сигнал превращается в дискретную серию чисел. Чаще всего непрерывный сигнал — это сигнал напряжения. Его дискретизирует и оцифровывает через равные промежутки времени электронная схема, которая называется «аналого-цифровой преобразователь» (рис. 1). На первый взгляд, из-за дискретизации теряется информация. Ведь на непрерывной кривой напряжения «бесконечно много» точек, но после дискретизации мы оставляем только их часть. Следовательно, потеряно бесконечное число точек между выбранными. И вот здесь звучит важнейшее утверждение теоремы дискретизации: в соответствующих условиях отдельные образцы содержат всю информацию, необходимую для идеального восстановления непрерывной функции напряжения, которая их произвела. В этом случае нет потери информации из-за дискретизации.

Эти соответствующие условия просты: входной сигнал должен изменяться достаточно медленно, чтобы его форма хорошо зафиксировалась в последовательности дискретных образцов. В частности, сигнал не должен иметь синусоидальных составляющих на частотах выше так называемой частоты Найквиста, которая равна половине частоты дискретизации:

$$

(1)

Например, если АЦП делает 10 000 измерений в секунду, то входной сигнал не должен превышать частоту 5000 Гц. Что произойдет, если входной сигнал будет меняться быстрее? Эти частотные компоненты нельзя будет реконструировать из образцов, поскольку их происхождение совершенно непонятно (рис. 1).


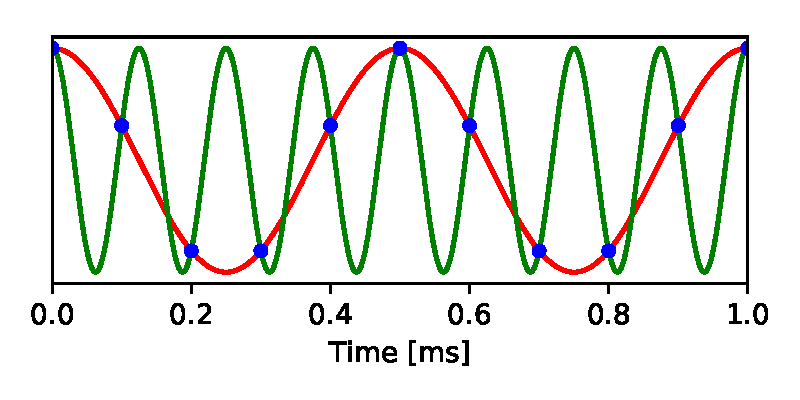
Рис. 1. Наложение. Синусоидальная волна с частотой 2 кГц (красная) дискретизируется с частотой 10 kS/s (синие точки). Другая синусоида с частотой 8 кГц производит точно такую же последовательность образцов. Таким образом, после дискретизации невозможно понять, исходный сигнал был на 2 кГц или на 8 кГц

Одинаковый набор образцов получается и из сигнала ниже частоты Найквиста, и из любого количества возможных сигналов выше частоты Найквиста. Это явление называется наложением (алиасинг), когда высокочастотный сигнал в дискретизированной форме может маскироваться под низкочастотный сигнал. Если для входящего сигнала не действует никаких ограничений, то наложение приводит к потере информации, потому что мы больше не можем восстановить исходный сигнал из дискретных образцов.

Как избежать наложения? Просто нужно перед дискретизацией устранить из аналогового сигнала частотные составляющие выше частоты Найквиста. Чаще всего это делается электронным фильтром нижних частот, который пропускает нижние частоты, но отсекает высокие. Благодаря повсеместному применению таких фильтров на их совершенствование потрачено немало инженерных усилий. В итоге обычный подход к конструированию системы сбора данных выглядит таким образом (рис. 2):

1. Определите необходимую полосу пропускания сигнала, который нужно зарегистрировать, а именно самую высокую частоту, которую впоследствии нужно восстановить. Это частота Найквиста $$ для вашей системы.

2. Пропустите сигнал через фильтр нижних частот, который отсекает все частоты выше $$.

3. Запустите дискретизация сигнала после фильтра с частотой $$.


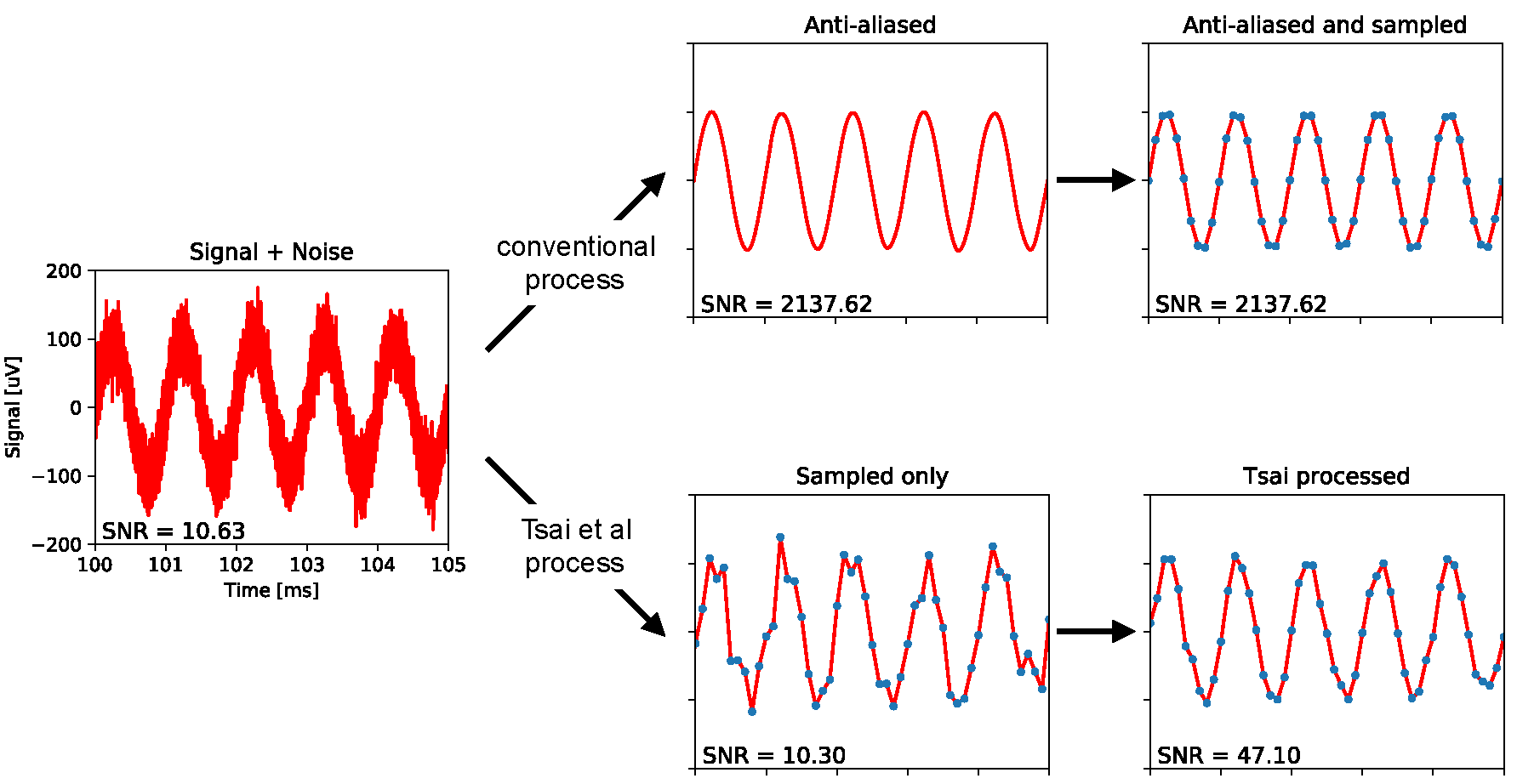
Рис. 2. Сравнение обычного сбора данных с процедурой, описанной в научной работе Цая и др. Слева: синусоидальная волна на частоте 1 кГц с амплитудой от пика до пика 200 мкВ, как в тестовых записях из научной работы. Добавлен белый гауссовский шум с полосой пропускания 1 МГц и среднеквадратичной амплитудой 21,7 мкВ. Сверху: стандартный подход применения фильтра для защиты от наложения с частотой отсечения 5 кГц, которая исключает бoльшую часть шума и таким образом улучшает соотношение сигнала к шуму (SNR) в 200 раз. Этот сигнал затем дикретизируется на 10 kS/s. Снизу: в научной работе Цая и др. сигнал сразу дискретизируется с сохранением того же низкого SNR. Затем следует цифровая обработка, которая немного увеличивает SNR. Все данные и обработка смоделированы с помощью этого кода

Что утверждают Цай и др.

Теперь рассмотрим конкретную ситуацию из научной работы Дэвида Цая и др. Они хотят записывать электрические сигналы от нейронов, для чего требуется полоса пропускания

$$

Так что они выбрали частоту дискретизации 10 kS/s. К сожалению, требуемый нейронный сигнал искажён из-за широкополосного теплового шума, неизбежного побочного продукта при записи. Спектр шума достигает 1 МГц с типичной среднеквадратичной амплитудой (rms) 21,7 мкВ. Авторы аппроксимируют его как белый гауссовский шум, то есть шум с постоянной плотностью мощности до отсечения на 1 МГц. (Ссылки на эти цифры: стр. 5 и рис. 11 из первой статьи; стр. 2, 5, 9 и рис. 2е в приложении из второй статьи).

Стандартной процедурой стала бы передача сигнала и шума через аналоговый фильтр для защиты от наложения с отсечением частот выше 5 кГц (рис. 2). Это оставит нетронутым нейронный сигнал, в то же время снизив мощность шума в 200 раз, потому что спектр шума срезается с полосы пропускания 1 МГц до всего лишь 5 кГц. Таким образом, оставшийся шум ниже частоты Найквиста будет иметь среднеквадратичную амплитуду всего 21,7 мкВ/$$ = 1,53 мкВ. Такое количество теплового шума совершенно безобидно. Это меньше, чем от других источников шума в эксперименте. Затем сигнал дискретизируется на частоте дискретизации 10 kS/s.

Вместо этого авторы полностью исключают фильтр и напрямую дискретизируют широкополосный сигнал+шум. В своей статье они подробно объясняют технические ограничения, связанные с нехваткой места на кремниевых устройствах в этом методе записи, из-за которых пришлось отказаться от фильтра. Но в итоге вся мощность шума вплоть до 1 МГц теперь попала в дискретизированный сигнал через наложение. Фактически, каждый образец загрязнён гауссовским шумом со среднеквадратичной амплитудой 21,7 мкВ. Это недопустимый уровень шума, потому что мы хотим различать сигналы нейронов на той же или меньшей амплитуде. Для справки, в некоторых популярных системах для записи мультинейронной активности уровень шума не превышает 4 мкВ.

Здесь Цай с коллегами демонстрируют поразительную «инновацию»: они говорят что можно применить хитрый алгоритм преобразования данных после дискретизации для восстановления оригинального широкополосного шума, вычесть этот шум из дискретизированных данных — и таким образом оставить чистый сигнал. Вот соответствующие цитаты, в дополнение к вышеуказанным: «Мы можем в цифровом виде восстановить спектральный вклад от высокочастотного теплового шума, а затем удалить его из данных с разреженной выборкой, тем самым минимизируя эффекты наложения, без использования фильтров защиты от наложения на каждом канале». И ещё одна: «Мы представляем архитектуры мультиплексирования без фильтров защиты от наложения на каждом канале. Данные разреженной выборки восстанавливаются с помощью стратегии сжатого считывания, включающей в себя статистическую реконструкцию и удаление теплового шума с грубым шагом дискретизации».

Какие доказательства они предъявляют для этого утверждения? Проведён только один эксперимент, который проверяет уменьшение шума с использованием реальных данных. Авторы записали синусоидальный тестовый сигнал на частоте 1 кГц с амплитудой 200 мкВ от пика до пика. Затем применили свою схему обработки для «удаления теплового шума». Выходной сигнал выглядит чище входного (рис. 2e из статьи; см. также симуляцию на рис. 2). Количественно шум сократился со среднеквадратичной амплитуды 21,7 мкВ до 10,02 мкВ. Это довольно скромное улучшение соотношения сигнала к шуму (SNR) в 4,7 раза (подробнее об этом ниже). Правильный фильтр для защиты от наложений перед дискретизацией или заявленная система удаления наложенного шума после дискретизации должны бы увеличить SNR в 200 раз. (Ссылки на процитированные результаты см. на рис. 2e-f из второй статьи и на рис. 7 из первой статьи).

Почему схема Цая и др. не может работать в принципе

Прежде чем перейти к конкретному разбору схемы обработки данных, предложенной в этих научных статьях, стоит подумать, почему она не может работать в принципе. Самое главное: если она работает, то это отменяет теорему Котельникова, которую поколения студентов-инженеров изучали в институтах. Сигнал белого шума в этих экспериментах дискретизируется с частотой в 200 раз ниже той, которая позволяет восстановить этот сигнала по теореме Котельникова. Так почему Цай с коллегами вообще решили, что схема может работать?

Авторы утверждают, что наложенный высокочастотный шум сохраняет некий отпечаток, что позволяет затем удалить его: «Воспользовавшись приведёнными выше характеристиками, мы можем в цифровом виде восстановить спектральный вклад от высокочастотного теплового шума, а затем удалить его из данных с разреженной выборкой, тем самым минимизируя эффекты наложения». Трудно понять, какие это могут быть характеристики. Их проще всего оценить по временнoй шкале. Белый гауссовский шум на полосе 1 МГц можно восстановить по временным рядам независимых образцов из идентичного гауссового распределения с частотой 2 млн образцов в секунду. Теперь возьмите эти временные ряды и сделайте подвыборку на 10 тыс. образцов в секунду, т.е. каждый 200-й из оригинальных образцов. Вы снова получите независимо и одинаково распределённые образцы, т. е. белый гауссовский шум на 10 kS/s. Ничто в этой серии образцов не показывает, что её источником является высокочастотный шум. Он отлично дискретизирован.


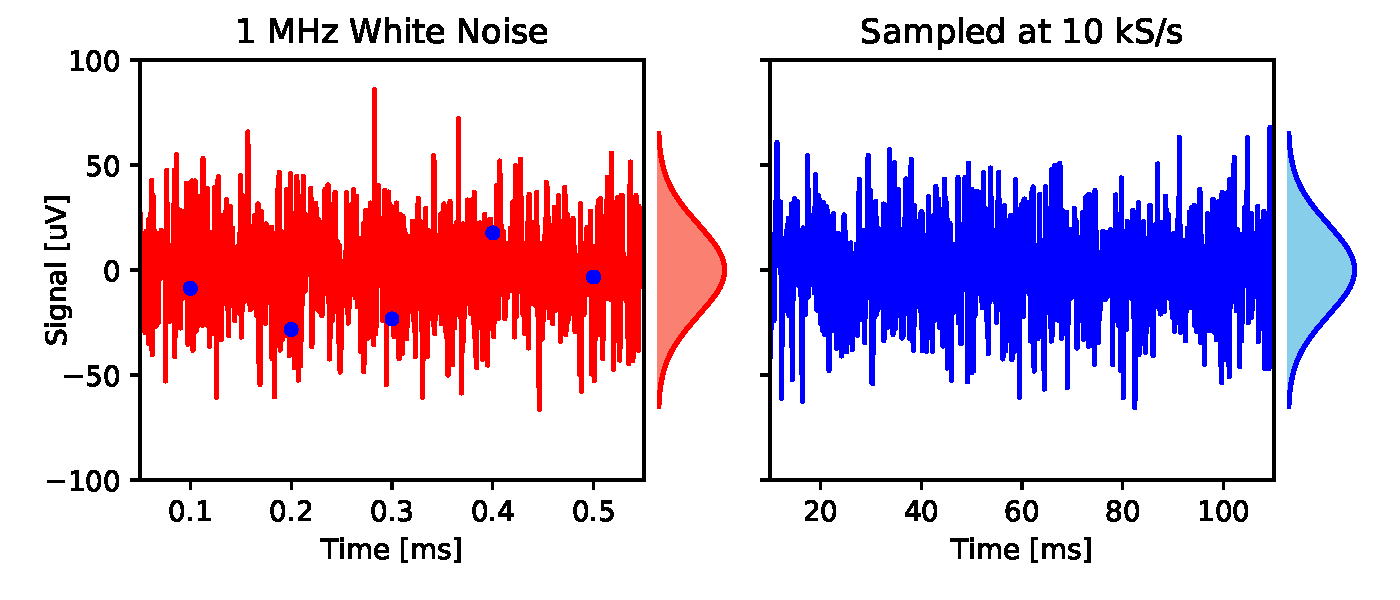
Рис. 3. Выборка белого гауссовского шума. Слева: белый гауссовский шум (красная линия) со среднеквадратической амплитудой 21,7 мкВ и полосой пропускания 1 МГц дискретизируется с частотой 10 kS/s (синие точки). Справа: дискретизированный сигнал с расширенной в 200 раз временной шкалой. Это тоже белый гауссовский шум, с тем же распределением амплитуды (поля графика), но полосой пропускания 5 кГц

Авторы также утверждают, что их алгоритм для восстановления белого гауссовского шума «избегает наложения за счёт использования концепций сжатого считывания». Принцип сжатого считывания (compressed sensing) заключается в том, что если сигнал проявляет известные закономерности, то можно дискретизировать его без потерь с частотой меньше, чем частота Найквиста. В частности, такой сигнал проявляет разреженное распределение в пространстве данных по определённым направлениям, что открывает возможности для сжатия. Это относится ко многим естественным источникам сигнала, таким как фотографии. К сожалению, белый гауссовский шум представляет собой абсолютно несжимаемый сигнал без каких-либо закономерностей. Распределение вероятностей для этого сигнала является круглой гауссовой сферой, которая в пространстве данных выглядит одинаково со всех сторон и просто не предусматривает никаких возможностей сжатия. Конечно, нейронные сигналы поверх этого шума содержат некоторые статистические закономерности (подробнее об этом ниже). Но они не помогают восстановить шум.

Как схема Цая и др. терпит неудачу на практике

Я написал код для алгоритма, описанного в научной работе Цая и др. При обработке симуляции авторского теста (синусоидальная волна 200 мкВ с шумом 21,7 мкВ) он выдаёт очищенную синусоидальную волну с шумом всего 10,2 мкВ (рис. 2), что ужасно близко к результату из научной работы 10,02 мкВ. Значит, я правильно эмулировал схему.

По ходу дела я натолкнулся на нечто похожее на серьёзную математическую ошибку. Это относится к убеждению авторов в том, что шум с недостаточным шагом дискретизации сохраняет некую подпись в результате наложения. Ссылаясь на Фурье-представление белого гауссовского шума, они пишут (раздел III.G): «В пространстве Фурье у векторных углов теплового шума (бесконечной длины) равномерное распределение с нулевым средним. Опять же, любое отклонение от этого идеала в сигналах конечной длины усредняется наложением спектров, когда содержимое складывается в первую зону Найквиста (в результате чего углы сходятся к нулю)». И аналогично «спектральные углы сходятся к нулю в варианте наложения теплового шума» (стр. 9 слева внизу). Это неверно. Фазовые углы описываемых здесь векторов Фурье имеют равномерное круговое распределение; у этого распределения нет среднего угла. После усреднения из-за нормализации некоторых из этих векторов фаза среднего вектора снова приобретает равномерное круговое распределение. Это подтверждается в пространстве Фурье, что проще оценить в непосредственном пространстве: подвыборка из белого гауссовского шума снова выдаёт вам белый гауссовский шум (рис. 3). Обоснование алгоритма Цая основано на этой ошибочной концепции, что фазовые углы каким-то образом усредняются до нуля.

Итак, каким же образом алгоритм Цая очищает синусоидальный тестовый сигнал? Это не так уж сложно. Если вы знаете, что сигнал — чистая синусоида, то остаётся лишь три неизвестных: амплитуда, фаза и частота. Очевидно, вы можете извлечь эти три неизвестных из 10 000 образцов шума, которые получаете каждую секунду. Можно сделать и гораздо эффективнее: найти наибольшую Фурье-составляющую в сэмплированной записи и обнулить все остальные. Это почти полностью устраняет шум (подробнее см. здесь). Алгоритм Цая примерно так и делает: сильнее подавляет внепиковые частоты в преобразовании Фурье, чем пиковые — и получает некую сумму синусоиды и подавленного шума (см. также рис. 9 в работе). Как мы увидим дальше, заявленная производительность не распространяется на реалистичные сигналы.

Что стало бы разумной схемой обработки?

Пример синусоидальной волны показывает, как на самом деле следует подходить к постпроцессингу данных. Попытка восстановить оригинальный шум безнадёжна по всем описанным выше причинам — нужно просто смириться с уровнем шума, который является результатом всех наложений спектров. И сосредоточиться на свойствах сигнала, который мы хотим выделить. Если сигнал имеет статистические закономерности, то можно использовать этот факт в свою пользу. Естественно, синусоидальная волна чрезвычайно регулярна — значит, она извлекается из шума почти с бесконечной точностью. Обычно у нас есть некие частичные знания по статистике сигнала. Например, форма энергетического спектра. У нейронных потенциалов действия частотные составляющие до ~5 кГц, но спектр не плоский во всём диапазоне (рис. 4).


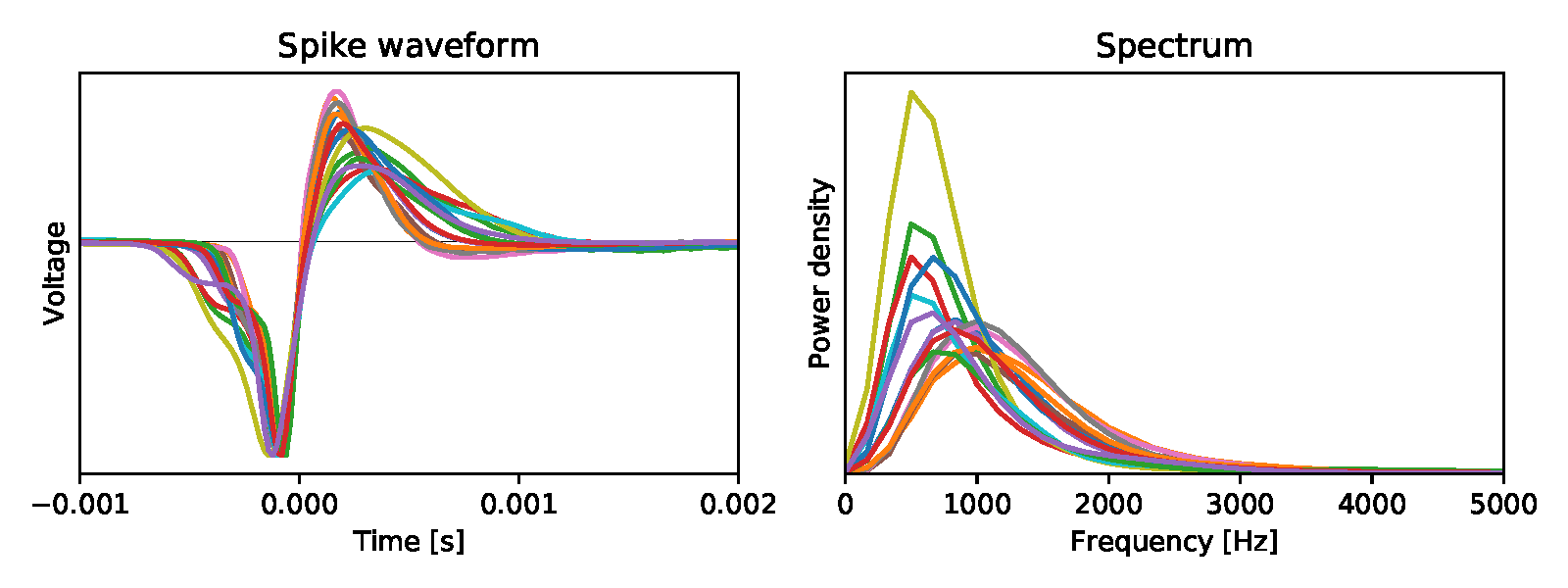
Рис. 4. Слева: усреднённые биоэлектрические потенциалы для 15 ганглиозных клеток сетчатки мыши [источник]. Справа: их энергетический спектр

Предположим, мы знаем энергетический спектр сигнала, и он отличается от спектра шума — как тогда обрабатывать данные выборки, чтобы оптимально восстановить сигнал? Это классическая задача, которую задают на курсе обработки сигналов. Оптимальный линейный фильтр для реконструкции c минимизацией средней квадратической ошибки называется фильтром Винера. По сути, он подавляет частотные компоненты, где шум относительно больше. Но алгоритм Цая — нелинейная операция (см. подробности здесь), так что теоретически он может превзойти фильтр Винера. Кроме того, из-за нелинейности невозможно предсказать эффективность алгоритма на более обычных сигналах по его производительности на синусоидальных сигналах (см. выше). Поэтому я сравнил алгоритм Цая с классическим фильтром Винера, используя различные предположения для спектра. В частности, сигнал был ограничен ниже частоты среза в диапазоне от 100 Гц до 5000 Гц, в то время как шум имел равномерный спектр в полосе 5 кГц:


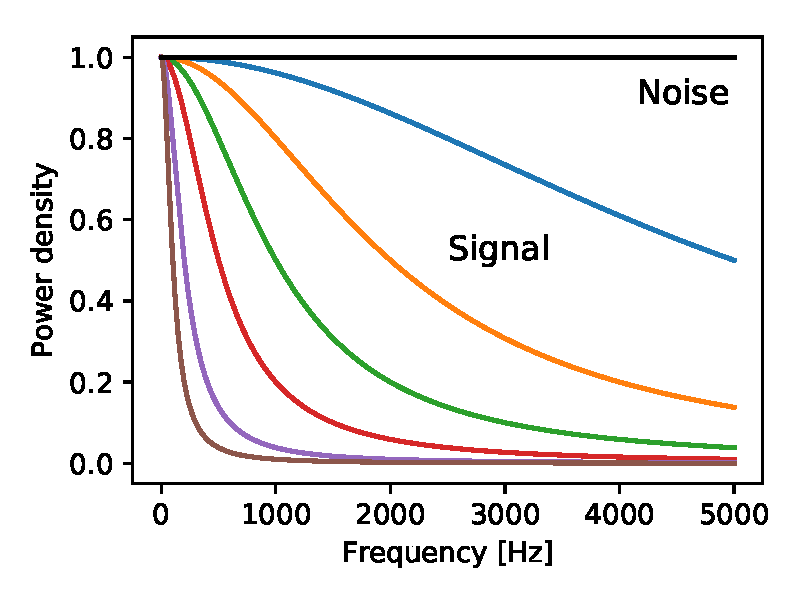
Рис. 5. Энергетический спектр сигнала (цветные линии) и шума (чёрная), используемые в расчётах на рис. 6. Шум гауссов и белый во всём диапазоне. Сигнал получен из гауссовского белого процесса, пропущенного через однополюсный фильтр нижних частот с частотами отсечки при 5000, 2000, 1000, 500, 200, 100 Гц.

Для каждого из этих сочетаний сигнала и шума я применил фильтр Винера и алгоритм Цая — и измерил соотношение сигнала к шуму (SNR) в результате (рис. 6).


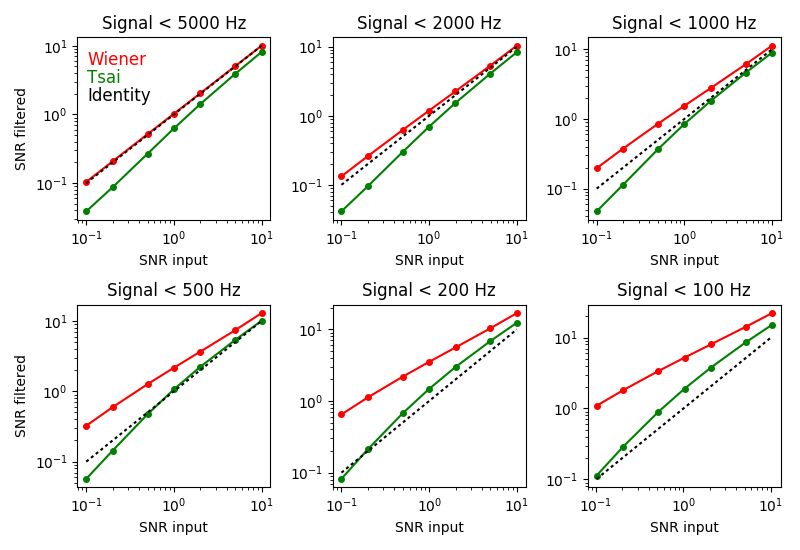
Рис. 6. Как алгоритм Цая и фильтр Винера изменяют SNR. Каждая панель соответствует различному энергетическому спектру сигнала (см. рис. 5). Сигнал и шум на разных SNR отложены по горизонтальной оси. Смешанный сигнал и шум пропустили через фильтр Винера или алгоритм Цая, а SNR выходного сигнала отложен по вертикальной оси. Красный — фильтр Винера; зеленый — алгоритм Цая; пунктир — подлинник.

Как и ожидалось, фильтр Винера всегда улучшает SNR (сравните красную кривую с точечным подлинником), и тем больше, чем сильнее отличие спектров сигнала и шума (панели от левой верхней к нижней правой). Во всех вариантах фильтр Винера превосходит алгоритм Цая в улучшении SNR (сравните красные и зелёные кривые). Кроме того, во многих случаях алгоритм Цая фактически ухудшает SNR (сравните зелёные и пунктирные кривые). Учитывая, что алгоритм основан на математических ошибках, это неудивительно.

Есть и более сложные схемы подавления шума, чем фильтр Винера. Например, мы знаем, что интересующие записи нейронной активности представляют собой наложение импульсоподобных событий — биоэлектрических потенциалов — чьи формы всплесков описываются всего несколькими параметрами. В рамках этой статистической модели можно разработать алгоритмы, которые определят среди шума оптимальные пиковые значения каждого из событий. Это активная область научных исследований.

Почему это важно для нейронауки

Исследователи из разных нейронаук активно стремятся увеличить число одновременно отслеживаемых нейронов. В этой области экспоненциальный прогресс, хотя довольно медленный, с удвоением каждые семь лет. Несколько проектов направлены на ускорение этого процесса путём создания крупномасштабных КМОП-микросхем с массивом из тысяч плотно расположенных электродов и мультиплексеров [в том числе работа Цая — примеч. пер.]. Это дорогие исследования. Чтобы довести электродные решётки до стадии прототипа, требуются миллионные вложения. Если успех подобного прибора основан на ошибочных представлениях о наложении и неоправданных ожиданиях от программного обеспечения, это может привести к дорогостоящим провалам и растрате ценных ресурсов.

Болезненным провалом такого рода стал массив Фромхерца. Сконструированный в сотрудничестве с Siemens за миллионы дойчмарок, он стал самым большим массивом биоэлектродов для своего времени, с 16 384 датчиками на площадке 7,8?7,8 мкм. Для экономии места и по другим причинам разработчики отказались от использования фильтров защиты от наложения. Наложение и прочие артефакты в итоге привели к уровню шума 250 мкВ, непригодному для каких-либо интересных экспериментов, так что инновационное устройство так никогда и не использовали в деле. А ведь такой исход можно было предсказать простым расчётом.

Если рационально предусматривать последствия наложения, то возможны полезные компромиссы. Например, в недавно созданном устройстве с кремниевыми штырьками тоже отсутствуют фильтры защиты от наложения в мультиплексерах. Но коэффициент субдискретизации всего 8:1, в результате чего избыточный шум не превышает критических значений. В сочетании с правильным восстановлением сигнала такая схема вполне жизнеспособна.

Кто проверял эту работу?

Как всегда, встаёт вопрос: эти драматические заявления Цая и др. прошли рецензирование? Неужели никого не удивило очевидное противоречие теореме отсчётов? Кто вообще рассматривал эти материалы? Ну, я их рассмотрел. Для другого журнала, где статью в итоге отклонили. До этого была длительная переписка с авторами, в том числе я дал им задачу удалить шум наложения из смоделированной записи (задача ниже, только без денежной награды). Авторы посчитали вызов обоснованной проверкой алгоритма, но полностью провалили тест. Каким-то образом это не поколебало их уверенности — и они представили точно такую же научную статью двум другим журналам. Эти журналы, видимо, после так называемого рецензирования, с радостью согласились на печать.

Как выиграть $1000

Конечно, есть вероятность, что я неправильно понял алгоритм Цая или, несмотря ни на что, существует иная схема восстановления наложенного белого шума после дискретизации. Чтобы поощрить творческую работу в этой области, предлагаю задачу: если вы можете сделать то, что утверждают Цай с коллегами, я дам вам $1000. Вот как это работает:

Сначала вы отправляете мне $10 на «почтовые расходы» (Paypal meister4@mac.com, спасибо). Взамен я высылаю файл данных, содержащий результат дискретизации сигнала и шума на 10 kS/s, где сигнал ограничен полосой ниже частоты Найквиста 5 кГц, а шум — это белый гауссовский шум с полосой 1 МГц. Вы используете алгоритм Цая или любую другую схему на ваш выбор, чтобы максимально удалить наложенный шум, и отправляете мне файл с вашей лучшей оценкой сигнала. Если вы сможете улучшить SNR в два или более раз, я заплачу вам 1000 долларов. Обратите внимание, что правильный фильтр защиты от наложений увеличивает SNR в 200 раз (рис. 2), а Цай утверждает, что увеличивает его более чем в четыре раза, поэтому я здесь немногого прошу. Для дополнительной технической информации см. код и комментарии в моём блокноте Jupyter.

Ещё несколько правил: предложение действует в течение 30 дней со дня публикации [20 марта 2018 года — примеч. пер.]. Выигрывает только первая квалификационная запись. Вы должны раскрыть используемый алгоритм, чтобы я мог воспроизвести его работу. После сражения с теоремой отсчётов вас может заинтересовать какая-нибудь другая задача, например, криптографическая атака на случайный seed, который я использовал для создания файла данных. Хотя мне было бы интересно узнать о таких альтернативных решениях, но я не буду платить за это 1000 долларов, а только верну ваши 10 долларов.

Наконец, я не хочу брать деньги у новичков. Прежде чем Вы пришлете мне $10, обязательно тщательно протестируйте свой алгоритм с использованием кода в моём блокноте Jupyter: его я буду использовать для оценки алгоритма.

Итоги

Пока никто не получил 1000 долларов, выводы следующие:

• Цай с коллегами разработали цифровой преобразователь без фильтра защиты от наложения, в результате чего получили примерно в 200 раз больше шума от термальных флуктуаций, чем можно было.
• Их алгоритм постобработки не делает ничего, чтобы нивелировать эффект наложения. В лучшем случае это попытка отделить нужный сигнал от искажающего наложенного шума. К сожалению, алгоритм основан на математических ошибках.
• Хорошо известны лучшие алгоритмы отделения сигнала от белого шума. Для синусоидальных сигналов (как приведённые авторами) такое отделение тривиально. Для ограниченных по полосе сигналов, спектральная мощность которых отличается от спектральной мощности шума, классическое решение — фильтр Винера. При всех проверенных условиях он показывает лучший результат, чем алгоритм Цая. При многих условиях алгоритм Цая ухудшает соотношение сигнала к шуму.
• На данный момент я предлагаю, чтобы разработчики аппаратуры придерживались древней мудрости «фильтруй перед выборкой!»