Продвинутое освещение

В уроке посвященном основам освещения мы кратко разобрали модель освещения Фонга, позволяющую придать существенную долю реализма нашим сценам. Модель Фонга выглядит вполне неплохо, но имеет несколько недостатков, на которых мы сосредоточимся в данном уроке.

Модель Блинна-Фонга

Модель Фонга является весьма эффективным приближением для расчета освещения, но при определенных условиях она может терять часть компоненты зеркальных бликов. Это можно заметить при малых значениях силы блеска (shininess) когда область зеркального отражения становится довольно большой. На рисунке ниже показано, что происходит, когда мы используем силу зеркального блеска 1.0 для плоской текстурированной поверхности:

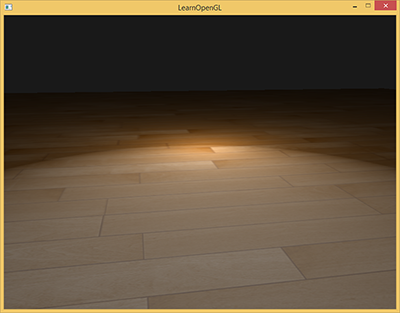
Как видите, область зеркального отражения имеет резко очерченную границу. Это происходит потому что угол между вектором обзора и вектором отражения не должен превышать 90 градусов, иначе их скалярное произведение становится отрицательным, что делает компоненту зеркальных бликов равной нулю. Вы можете подумать что в этом нет ничего страшного, потому что мы и не должны получать какой-либо освещенности при углах свыше 90 градусов, верно?

Не совсем. Это применимо только по отношению к диффузной компоненте, где угол выше 90 градусов между вектором нормали и направлением света означает, что источник света находится ниже освещаемой поверхности, и, следовательно, вклад диффузного освещения должен равняться нулю. Однако в случае с зеркальной компонентой мы измеряем не угол между направлением света и нормалью, а угол между векторами обзора и отражения. Взгляните на следующие два рисунка:

Теперь проблема становится очевидной. Слева мы видим привычную нам картину Фонговского отражения с ? менее 90 градусов. На правом рисунке угол ? между направлениями зрения и отражения больше 90 градусов, в результате чего вклад зеркального освещения аннулируется. Обычно это не причина для беспокойства, так как вектор обзора зачастую заметно удален от вектора отражения. Но при малых значениях силы зеркального блеска радиус области отражения становится достаточно большим, и дает заметный вклад в общую картину. Используя модель Фонга мы аннулируем этот вклад при углах больше 90 градусов (как видно на первом изображении).

В 1977 году Джеймсом Ф. Блинном (James F. Blinn) была представлена модель освещения Блинна-Фонга, как дополнение к модели Фонга, которой мы пользовались до сих пор. Она во многом схожа с моделью Фонга, но использует немного иной подход к расчету зеркальной компоненты, что позволяет решить нашу проблему. Вместо того, чтобы полагаться на вектор отражения, мы используем так называемый медианный вектор (halfway vector), который представляет из себя единичный вектор точно посередине между направлением обзора и направлением света. Чем ближе этот вектор к нормали поверхности, тем больше будет вклад зеркальной компоненты.

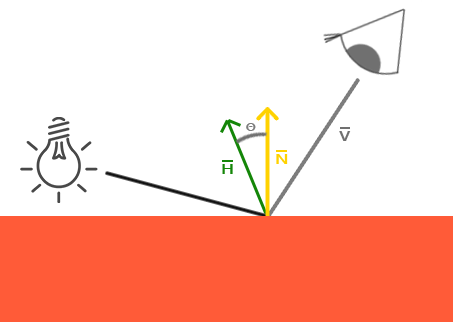
Когда направление обзора полностю совпадает с (теперь уже мнимым) вектором отражения, медианный вектор совпадает с нормалью к поверхности. Таким образом, чем ближе направление обзора к направлению отражения, тем сильнее становится зеркальный блеск.

Очевидно, что вне зависимости от направления, с которого смотрит наблюдатель, угол между медианным вектором и нормалью к поверхности никогда не превысит 90 градусов (если, конечно, источник света не находится ниже поверхности). Благодаря этому мы получаем несколько иные результаты по сравнению с Фонговским отражением, и в целом картина выглядит более визуально правдоподобной, особенно при низких значениях силы зеркального блеска. Именно модель освещения Блинна-Фонга использовалась в более раннем, фиксированном конвейере OpenGL.

Найти медианный вектор легко: нужно сложить вектор направления света с вектором обзора и нормировать результат:

$\$\$display\$\$\backslash vec\; H\; =\; \backslash frac\{\backslash vec\; L\; +\; \backslash vec\; V\}\{||\backslash vec\; L\; +\; \backslash vec\; V\; ||\}\$\$display\$\$$

На языке GLSL это выглядит так:

vec3 lightDir   = normalize(lightPos - FragPos);
vec3 viewDir    = normalize(viewPos - FragPos);
vec3 halfwayDir = normalize(lightDir + viewDir);

Таким образом расчет зеркальной составляющей сводится к простому вычислению скалярного произведения между нормалью к поверхности и медианным вектором, чтобы получить значение косинуса угла между ними, которое мы снова возводим в степень силы зеркального блеска:

float spec = pow(max(dot(normal, halfwayDir), 0.0), shininess);
vec3 specular = lightColor * spec;

Собственно, это всё что касается модели Блинна-Фонга. Единственное различие между зеркальным отражением в моделях Блинна-Фонга и Фонга заключается в том, что теперь мы измеряем угол между нормалью и медианным вектором вместо угла между направлением обзора и вектором отражения.

Используя медианный вектор для расчета компоненты зеркальных бликов мы больше не будем иметь характерной для модели Фонга проблемы с резкой границей области зеркального отражения. На изображении ниже показана область зеркального отражения обоих методов при силе зеркального блеска 0.5:

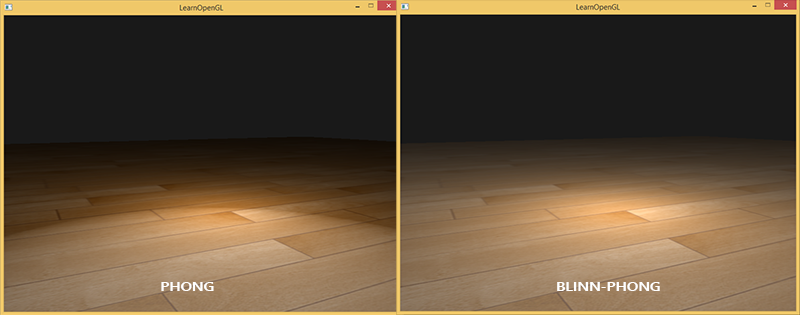
Еще одно небольшое различие между моделями Фонга и Блинна-Фонга заключается в том, что угол между медианным вектором и нормалью к поверхности часто меньше угла между векторами обзора и отражения. Поэтому, чтобы получить аналогичные модели Фонга результаты, значение силы зеркального блеска должно быть немного выше. Эмпирически установлено, что оно где-то в 2-4 раза больше по сравнению с моделью Фонга.

Ниже приведено сравнение зеркальной компоненты между моделями с силой зеркального блеска равной 8 для модели Фонга и 32 для модели Блинна-Фонга:

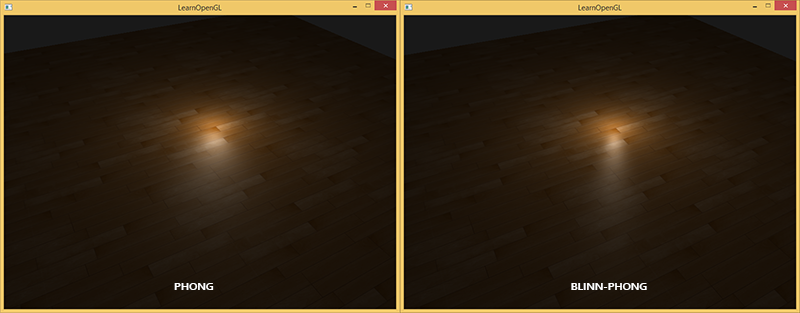
Как видно, зеркальная компонента Блинна-Фонга более резкая. Обычно требуется небольшая подгонка, чтобы получить результаты аналогичные полученным ранее с использованием модели Фонга, но, в целом, освещение Блинна-Фонга дает более правдоподобную картину.

Для данной демонстрации мы использовали простой фрагментный шейдер, который переключается между обычным отражением Фонга и отражением Блинна-Фонга:

void main()
{
    [...]
    float spec = 0.0;
    if(blinn)
    {
        vec3 halfwayDir = normalize(lightDir + viewDir);  
        spec = pow(max(dot(normal, halfwayDir), 0.0), 16.0);
    }
    else
    {
        vec3 reflectDir = reflect(-lightDir, normal);
        spec = pow(max(dot(viewDir, reflectDir), 0.0), 8.0);
    }
    [...]

Исходный код данного урока вы найдете здесь. Нажимая клавишу b, вы можете переключаться с модели Фонга на модель Блинна-Фонга и обратно.

Оригинал статьи.