континуума.). Данный метод доказывает несчетность подмножества действительных чисел, принадлежащих диапазону [0,1]. Однако, если присмотреться к доказательству, становится ясно, что оно не учитывает экспоненциальный рост возможных вариантов с каждым увеличиеним порядкового номера в десятичной дроби.
Кантор рассуждает следующим образом (но только в отношении бесконечных десятичных дробей): расположем десятичные дроби произвольным образом в виде списка, далее пронумеруем их и рассмотрим диагональ. Если к каждой цифре на диагонали прибавить 1, то мы получим число, которого нет в данном списке. Вот как раз таки этот момент на интуитивном уровне вызывает сомнение.
Недостаток диагонального метода
Для того, чтобы понять о чем речь, давайте попробуем рассмотреть идею диагонального метода на следующем примере. Рассмотрим конечные дроби вида: 0,a1a2a3a4a5, сформируем из них список так, чтобы получился квадрат размером 5*5, как это показано на рисунке ниже:

Применим метод Кантора, и действительно, числа 0,22226 нет в данном квадрате. Но, оно есть в прямоугольнике 5*n5, где 5 – количество знаков после запятой, а n – количество цифр в используемой системе исчисления (в данном примере, n=10). Это объясняется тем, что количество комбинаций всех возможных дробей, длина которых составляет 5 знаков после запятой, равно n5.
Устремляя размер квадрата до бесконечности, получаем то, что называется диагональным методом Кантора. Но в бесконечность нужно устремлять не квадрат, а прямоугольник, размером m*nm, где m – количество позиций после запятой, m --> ?.
Идея моего подхода
Чтобы пронумеровать все действительные числа, принадлежащие диапазону [0, 1], их надо располагать в виде экспоненциально растущего дерева. Рассмотрим десятичные дроби, записанные в двоичной системе. Пусть k – количество знаков после запятой, n – размер алфавита системы счисления. Тогда количество возможных вариантов дробей начиная с k=1 и до ? будет функцией от k, это видно на рисунке ниже:
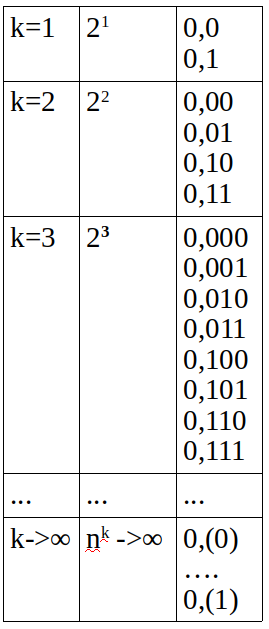
Назовем каждую строку в вышеприведенной таблице – уровнем. Таким образом k – это и номер уровня, и количество знаков после запятой одновременно.
Введем два порядковых номера:
- общий счетчик (C, Counter), используется для последовательной нумерации всех чисел из диапазона [0,1];
- счетчик уровня (L, per Level counter), используется для нумерации чисел на каждом уровне отделььно, обнуляется при переходе на следующий уровень. Для первого уровня L примет значения 1 и 2, для второго — 1, 2, 3 и 4 и т.д.
Изобразим все двоичные десятичные дроби в виде в виде двоичного дерева, как в таблице ниже:

Каждая отдельная цифра в позиции десятичного числа располагается в отдельной ячейке. Напротив каждой такой цифры записываем 2 индекса C и L следующим образом: NCL, где N – значение цифры.
Cтановится очевидно, что С и L – это функции от k и цифр самого числа N: С = fC(k; N), L = fL(k; N). Также становится очевидно, что мы можем пронумеровать все числа из диапазона [0,1], т.к. мы последовательно проходим по каждому уровню и последовательно нумеруем все возможные комбинации на данном уровне.
Осталось вывести аналитическую зависимость для счетчиков C = fC(N) и L = fL(k;N).
Для удобства обозначим L(k;N) как Lk.
Будем считать, что L0 — 1 = 0.
Если внимательно изучить таблицу, то вырисовывается следующая закономерность:
Lk = (Lk-1 — 1)*S + N + 1,
где k >= 1, N – текущая цифра в дроби, S = |{0,1}| = 2 – размер алфавита двоичной системы счисления. Запись |A| означает мощность множества A, для конечного множества – это количество элементов в нем.
Очевидно, что C содержит сумму всех комбинаций для всех предыдущих уровней плюс L числа для текущего уровня, т.е. C(N) = ?i?[1,k-1]2i + L(k; N).
Примеры
Рассмотрим произвольное число 0,0101. Его порядковый номер C(0,0101) = 21 + 22 + 23 + L4 = 2 + 4 + 8 + 6 = 20.
Расчеты:
L1 = (L0-1)*2 + 0 + 1 = 0*2 + 0 + 1 = 1
L2 = (L1 — 1)*2 + 1 + 1 = (1 — 1)*2 + 1 + 1 = 2
L3 = (L2 — 1)*2 + 0 + 1 = (2 — 1)*2 + 0 + 1 = 3
L4 = (L3 — 1)*2 + 1 + 1 = (3 — 1)*2 + 1 + 1 = 6
Визуализация:

Рассмотрим произвольное число 0,1001. Его порядковый номер C(0,1001) = 21 + 22 + 23 + L4 = 2 + 4 + 8 + 10 = 24.
L1 = (L0 — 1)*2 + 1 + 1 = 0*2 + 1 + 1 = 2
L2 = (L1 — 1)*2 + 0 + 1 = (1 — 1)*2 + 0 + 1 = 3
L3 = (L2 — 1)*2 + 0 + 1 = (2 — 1)*2 + 0 + 1 = 5
L4 = (L3 — 1)*2 + 1 + 1 = (3 — 1)*2 + 1 + 1 = 10
Визуализация:

Выводы
Таким образом мы получили алгоритм, который последовательно нумерует абсолютно все действительные числа из диапазона [0,1], при этом, если взять произвольную десятичную дробь произвольной длины, то мы можем вычислить ее уникальный прядковый номер.
P.S. Если предложенный мной алгоритм имеет ошибку, которую я, в силу своей невнимательности, не вижу – большая просьба написать об этом в комментариях.
P.P.S Если же ошибки нет – то получается, что |[0,1]| = |N|! Т.е. ВСЕ действительные числа из диапазона [0,1] можно пронумеровать!
Комментарии (53)

vilgeforce
14.05.2018 12:13+5Вы пробовали найти «номер» для Pi/4 например?

FeRViD Автор
14.05.2018 12:25Но мы же можем последовательно вычислять последовательность знаков после запятой, после чего алгоритмически вычислять порядковый номер для Pi/4. Просто это будет бесконечный процесс, т.к. у числа бесконечно много знаков после запятой. Но т.к. есть алгоритм, то и есть взаимо-однозначное соответсвие.

anjensan
14.05.2018 12:28+2Но т.к. есть алгоритм, то и есть взаимо-однозначное соответсвие.
Простите, но соответсвтвие между чем и чем?
Между числом, и порякдовым номером, которого не существует, ибо алгоритм никогда не выполнится, так?
FeRViD Автор
14.05.2018 12:44ну тогда надо говорить так — между числом которогоне существует и порядковым номером, которого не существует.
Число Pi/4 мы уточняем знак за знаком, это бесконечный итеративный процесс. По мере получения очередного знака, мы получаем конкретное число и вычисляем для него порядковый номер.
Т.е. бесконечную непереодическую дробь — можно рассматривать как несуществующее число, а можно рассматривать, как результат работы некоторого бесконечного алгоритма, который на каждом шаге выдает очередную цифру и в этом смысле порядковый номер можно тоже рассматривать как некое число, являющееся результатом работы бесконечного алгоритма.
multiprogramm
14.05.2018 13:16+6Ну, если рассуждать в ключе, что иррациональных чисел не существует, то и доказывать ничего не нужно дополнительно: нумеруем рациональные и всё. Что, как я понял, и было сделано. Вот только иррациональные числа существуют сами по себе, и это доказано строго математически. А то, что мы можем «пощупать» только их приближения — это не проблема иррациональных чисел и уж никак не опровержение их существования.
А что является результатом работы алгоритма, который не завершится никогда? Рассуждая на пальцах: либо «ничего» (или другой определённый конкретный ответ), и тогда все иррациональные числа имеют «одинаковый номер» — нет однозначности, либо «не определено», и тогда мы не можем сравнить номера, как следствие, не можем проверить однозначность соответствия.
Или, например, так: вот для двух разных «конечных рациональных» чисел при грамотно построенной нумерации (например, по квадрату) всегда будет два конечных номера, которые можно сравнить и убедиться, что номера разные. А как сравнить между собой два бесконечных номера?
FeRViD Автор
14.05.2018 13:27Ну в таком же ключе можно сказать, что и номер для такого числа существует сам по себе.
Есть существование числа самого по себе, а есть конкретная запись числа. Мы можем абстрагироваться от конкретных цифр числа — просто введя обозначение, например Pi/4. Точно также, мы можем асбтрагировать номер этого числа, пусть порядковый номер числа Pi/4 будет C(Pi/4). И в этом смысле он также существует сам по себе. Где противоречие?
anjensan
14.05.2018 13:37+1Смысл в том, что по номеру можем восстановить число.
Точно также, мы можем асбтрагировать номер этого числа, пусть порядковый номер числа Pi/4 будет C(Pi/4).
Отлично. И какому числу сооствествует номер С(Pi/4)+1?
FeRViD Автор
14.05.2018 13:52Вот тут надо подумать, возможен ли алгоритм для обратного поиска, чтобы по номеру однозначно определять десятичную дробь, которая ему соответствует.
Пока идей как это сделать нет.
anjensan
14.05.2018 14:03+1Ну а раз алгоритма обартного поиска нету, то и некорректно заявлять
Но т.к. есть алгоритм, то и есть взаимо-однозначное соответсвие.
А это значит что ваши «доказательства» бездоказательны :)
Я даже упрощу задачу… Вместо нахождения самого числаRev(C(Pi/4) + 1)просто определите больше оно или меньше чемPi/4.
FeRViD Автор
14.05.2018 14:28Согласен, что взаимо-однозначного соответсвия нет, но алгоритм устанавливает соответсвие в одну сторону каждому R на [0,1] ставит в соответствие N. Для обратной задачи нужно подумать либо доказать, что такого алгоритма нет.
Еще один изъян алгоритма, описан с комментарии: habr.com/post/358526/#comment_11354864.
Как его устранить — пока тоже нет идей.
anjensan
14.05.2018 14:41+2Согласен, что взаимо-однозначного соответсвия нет
Замечатель, получается заголовок статьи прямо сейчас врет. Надеюсь вы его поправите.
но алгоритм устанавливает соответсвие в одну сторону каждому R на [0,1] ставит в соответствие N
И все равно вы за свое… Еще одна задачка для вас: что больше, C(Pi/4) или C(Pi/3) (вы же их «пронумеровали», т.е. дали порядковый номер)?

FeRViD Автор
14.05.2018 17:33Pi/3 > 1, выходит за интервал [0,1]. Над обобщением для чисел за пределами диапазона [0,1] — еще не размышлял.
Предлагаю рассмотреть числа: Pi/4 и Pi/5.
Алгоритм проходит по всем уровням последовательно, сверу вниз, а на каждом уровне слева направо, от меньших чисел к большим, поэтому C(Pi/5) < C(Pi/4).
anjensan
14.05.2018 18:01Pi/3 > 1, выходит за интервал [0,1].
Да, мой косяк. Надо конечно Pi/5.
Алгоритм проходит по всем уровням последовательно, сверу вниз, а на каждом уровне слева направо, от меньших чисел к большим, поэтому C(Pi/5) < C(Pi/4).
Как интересно… ну разC(Pi/5) < C(Pi/4)то чему тогда равноC(Pi/4) - C(Pi/5).
FeRViD Автор
14.05.2018 18:34Рассматривая проблему континуума с алгоритмической точки зрения, любое рациональное число из [0,1] — вычисляется бесконечно долго, а т.к. его порядковый номер — функция от цифр самого числа, то и порядковый номер таких чисел вычисляется бесконечно долго. Поэтому результаты арифметических действий над такими номерами тоже вычисляются бесконечно долго.

FeRViD Автор
14.05.2018 18:42в предыдущем комментарии, я опечатался, вместо «рациональное» должно быть "иррациональное".

kmu1990
14.05.2018 22:31Вы путаете теплое с мягким. Долго оно вычисляется или нет не существенно, существует оно или нет вот в чем вопрос.
В вашем подходе, чтобы число было пронумерованно, должна существовать запись этого числа принадлежащая какому-то уровню. Соответственно вопрос, существует ли такая запись иррационального числа (например, Pi/5, как предрагалось раньше), которая принадлежит хоть какому-то уровню?
Или другими словами, вы утверждаете, что ваш алгоритм перебирает все вещественные числа, но доказательство этого вы не привели, а лишь ограничились фразой:
мы можем пронумеровать все числа из диапазона [0,1], т.к. мы последовательно проходим по каждому уровню и последовательно нумеруем все возможные комбинации на данном уровне
Которая говорит толькто то, что вы можете пронумеровать все числа, которые можно вписать в вашу таблицу, но из этого никак не следует что все вещественные числа могут быть вписаны в вашу таблицу. На этом диагональный принцип как раз и строится, он предъявляет число, которое нельзя вписать в таблицу, пусть и немного другой структуры.

Deosis
15.05.2018 07:49Проблема в том, что и для многих рациональных чисел не подобрать номер.
Например 1/3.

FeRViD Автор
15.05.2018 10:48Кстати, мысль по поводу обратно поиска.
Возьмем сколь угодно большое число, X.
Разложим его на сумму степеней двойки: X = 2^1 + 2^2 +… + 2^k + L(k+1)
Если L(k+1) — нечтное — то цифра на уровне k+1 — 1, если четное — то — 0.
Далее, используя соотношение: Lk = (Lk-1 — 1)*S + N + 1, мы всегда сможем вычислить порядковый номер цифры для предыдущего уровня.
Т.о. двигясь в сторону корня дерева (вверх) и мы в итоге построим конкретное десятичное число, которому соответсвует данный номер.
Но это подразумевает, что мы должны использовать опредленное значение номера. Т.е. если рассмотреть номер для числа Pi/5 — число С(Pi/5), то обратное восстановление невозможно в силу того, что сам номер — не определен, т.к. он вычисляется бесконечно долго. Как-то так…
anjensan
15.05.2018 12:01У вас тут прямо новая, нескучная математика…
Возьмем сколь угодно большое число, X.
Ну давайте, разложите C(Pi/4). Даже любопытно.
Разложим его на сумму степеней двойки: X = 2^1 + 2^2 +… + 2^k + L(k+1)
Если L(k+1) — нечтное — то цифра на уровне k+1 — 1, если четное — то — 0.
Кстати, а C(Pi/4) само четное или нечетное?
Т.о. двигясь в сторону корня дерева (вверх) и мы в итоге построим конкретное десятичное число, которому соответсвует данный номер.
Движение как-бы надо начать из некой позиции.
Т.е. если рассмотреть номер для числа Pi/5 — число С(Pi/5), то обратное восстановление невозможно в силу того, что сам номер — не определен, т.к. он вычисляется бесконечно долго. Как-то так…
Т.е. все что вы тут предложили ранее, это не работает и чушь, причем вы это сами понимаете?

multiprogramm
14.05.2018 13:47+3Нет. Так просто сказать нельзя. И про иррациональные числа тоже так просто сказать нельзя. Всё нужно доказывать. И доказательство существования иррациональных чисел есть. А доказательство существования этого номера — нет. Есть только попытки итерационного приближения.
Число существует не потому что мы дали ему имя/обозначение. Я тоже могу ввести число Гладина, которое в поле действительных чисел при делении на единицу не равно себе. От этого оно существовать не станет.
FeRViD Автор
14.05.2018 18:40а разве это действие
Я тоже могу ввести число Гладина, которое в поле действительных чисел при делении на единицу не равно себе. От этого оно существовать не станет.
не потребует внесения изменения в аксиоматику поля?
А в моих рассуждениях разве есть противоречие аксиомам поля?

technic93
14.05.2018 19:18пусть порядковый номер числа Pi/4 будет C(Pi/4).
Отлично а зачем тогда ваше доказательство? Пусть для любого числа x из R его номер это n(x), где n пренадлежит N. Как вам такое "доказательство"?
Ваш алгоритм С никогда не заканчивается потому что для Pi/4 он выглядит так:
while True: find_next_digit()
Задача о том чтобы придумать несчетное число алгоритмов параметризованных вещесвтенным числом и задача о том чтобы построить взаимно однозначное соответсвие между множеством [0,1] и N — это разные задачи.
Но верно то, что между множеством Q и N бикция таки есть.

youngmysteriouslight
15.05.2018 01:08Есть существование числа самого по себе, а есть конкретная запись числа.
Кстати, вот интересное следствие:
Существуют действительные (иррациональные) числа, которые не могут быть записаны конечным числом знаков, какую бы систему обозначений мы не приняли исходно.
P.S. кстати, а как в рамках рассматриваемой статьи определяется понятие действительного числа?

SmallSnowball
15.05.2018 10:49Не совсем, счетность множества предполагает, что каждому элементу множества можно проставить в соответствие натуральное число. Pi/4 в таком алгоритме не имеет натурального числа в принципе, как раз потому что этот алгоритм дает числу конечный номер только в том случае, если дробь конечная

EndUser
14.05.2018 12:20+1«Устремляя размер квадрата до бесконечности» — вот именно. На этом дальнейшие выкладки отметаются.

ivan19631224
14.05.2018 12:36+2Вы пронумеровали все конечные десятичные (ну или двоичные) дроби. Но какому натуральному числу в вашей схеме будет соответствовать число 0,01001000100001… или примеры выше с Pi? Ваш алгоритм просто не завершится для этих чисел, нельзя просто сказать "и так далее до бесконечности", в этом то вся и проблема.
Бесконечные непериодические дроби у вас не получилось пронумеровать, т.е. не получилось построить биекцию (взаимно однозначное соответствие).
FeRViD Автор
14.05.2018 12:49habr.com/post/358526/#comment_11354670
Я просто предлагаю рассматривать биекцию как алгоритм. Потому что само понятие «бесконечное число» по смысло ближе всего к понятию «бесконечно работающий алгоритм, генерирующий это число». В этом смысле мы можем пронумеровать числа на [0,1]. Просто мы никогда не узнаем точного номера числа 0,01001000100001…, т.к. никогда не узнаем, как выглядит число полностью.
ivan19631224
14.05.2018 13:08+3Биекция не алгоритм (в конечном итоге). Это взаимно-однозначное отображение, т.е. соответствие каждому элементу одного множества ровно одного элемента другого множества и наоборот. Вы не можете сказать, что вот этому числу соответствует не элемент множества, а некий "бесконечно работающий алгоритм". 0.010010001… — это конкретная точка на прямой, и если построена биекция, то этой точке должно соответствовать конкретное число, а не нечто бесконечно генерящееся.
"Просто мы никогда не узнаем точного номера числа..." — неужели вы не понимаете, что такого числа просто не существует в вашей схеме?

jahr
14.05.2018 16:37+2Вы слишком вольно обращаетесь с понятием «бесконечный». У него есть точное определение (см. раздел любого учебника по матану про пределы), и бесконечная десятичная дробь будет соответствовать этому определению, а Ваш бесконечный алгоритм — нет, т.е. это — совсем не та бесконечность, и приравнивать их нельзя, это просто одинаково звучащие, но обозначающие разное слова в русском языке. Поэтому математики и используют кванторы и т.п. формальную терминологию.)

ShashkovS
14.05.2018 13:37+1Это же треш. У вас в последней строчке таблицы с числом цифр несчётное количество последовательностей. И нет последовательности, «следующей» за 0,(0).
Судя по вашим комментариям, вы представляете себе биекцию «вычислимых» чисел (для которых есть алгоритм, вычисляющий каждую цифру) и натурального ряда. Он существует. Но описываете не его. Всё это из-за того, что для бесконечной дроби не может быть следующей дроби. Какой хвост бы не поменяли, всё равно пропустим континуум чисел.

Aquahawk
14.05.2018 14:02Я тут ещё подумал над примером, может вам поможет с другой стороны подойти. Вы же понимаете что 0,9(9) оно же 0.9999… до бесконечности это строго 1. Т.е. это разные записи одного и того же числа. Это не бесконечно близкое число, это строго одно и тоже число. Также как и 0,49(9) == 0.5 Это разные способы записать одну и ту же точку на числовой прямой. Я правильно понимаю что в вашем алгоритме для 0,5 и 0,49(9) получится разный порядковый номер?

FeRViD Автор
14.05.2018 14:36Да, получается, что алгоритм создает для двух разных форм записи одного и того же числа разные порядковые номера. И если решать задачу обратного отображения N -> R, то два разных N будут фактически соответсвовать одной и той же дроби, просто записанной в разных формах. Пока не знаю, как это устранить.

VaalKIA
14.05.2018 14:44Вы полегче с переходами к бесконечности: одна треть, в бесконечности, какое число означает? Проблема фундаментальна и заключается в том, что не все дробные числа можно выразить в десятичной или, к примеру, двоичной системе исчисления. Например, 0.2 в двоичной выразить нельзя и чем больше основание, тем меньше таких чисел. Вообще, переход от бесконечности к чему-то означает внесение бесконечно малой погрешности, и когда речь идёт о подсчёте площади криволинейной фигуры, это одно, а когда речь идёт о абсолютно точных вирутальных числах, это уже подлог, потому что погрешность никуда не девается, хоть и бесконечно малая.

Aquahawk
14.05.2018 15:37+2число 1,3(3) не имеет конечной записи. А число 0.9(9) имеет конечную запись, это 1. Нет там никакой погрешности. Это прям ровно именно тоже число.

capslocky
14.05.2018 17:30Была такая хорошая задача на первом курсе: установите биекцию между [0,1] и [0,1).

yurixi
14.05.2018 19:59У меня идея еще лучше — надо составить последовательность всех чисел просто по порядку как они встречаются. Можно доказать что в этой последовательности находятся все числа — так как какого числа не хватись — то «вот же, положила». И даже если пройтись по всему ряду и составить число которого там нет, то следующим пойдет именно оно.
Только, если добавлять число «после» проверки нельзя, а можно только «до», то такой прикол не получится. Так как для любого набора бесконечного количества чисел можно найти такое, которое не совпадает со всеми по такой характеристике, которая счетно адресуется, вроде цифры с тем же номером, под которым число подсчитано.
Говоря проще, погружение в детализацию происходит быстрее чем перебор, и значит, различие вводится гораздо проще чем вводится равенство. Поэтому, различие счетного множества и несчетного легче доказывается, чем опровергается.
Но если думать, что счетное множество это не только те элементы которые можно посчитать, но и те которые можно «продолжать считать», то получится вот что:
«Мы эти понятия не различаем, поэтому они не различаются».
FeRViD Автор
15.05.2018 10:36Алгоритм не пропускает ни одного числа, т.к. он подсчитывает все числа в таблице m*nm.
m — это количество знаков после запятой, n — алфавит системы счисления.
Иными словами, алгоритм подсчитывает количество размещений с повторениями для каждой позиции после запятой. Количество размещений увеличивается экспоненциально с каждой следующей позицией.
Для десятичных дробей, записанных в десятичной системы счисления алгоритм последовательно будет выдавать такой результат (порядковые номера присваиваются слева направо):
m = 1
0,0; 0,1; ...; 0,9 — всего 10 комбинаций.
m = 2
0,00; 0,01; 0,02; ...; 0,10; 0,11; ...; 0,90; 0,91; ...; 0,99
Т.о. для m=2 получается 100 комбинаций, а для обоих уровней общее количество комбинаций — уже 110.
m = 3
Т.о. для m=3 получается 1000 комбинаций
…
m = k
Количество всевозможных комбинаций — 10k
k — растет линейно, а количество комбинаций, соответствующее k — экспоненциально.
koldyr
15.05.2018 13:44Не более чем счётное объединение не более чем счётных множеств не более чем счётно. Поэтому что у вас с какой скоростью растет абсолютно не важно.

kmu1990
15.05.2018 21:361. Любое число которое ваш перечислящий алгоритм выдает имеет конченое число знаков в какой-то системе счисления — это уже точно не все числа.
2. Давайте посмотрим на ваши таблицы и заметим что талица уровня 2 включает все числа, которые есть на уровне 1, таблица уровня 3 включает все числа которые есть в таблицах на уровнях 1 и 2, и так далее. Т. е. другими словами несколько уровней не добавляют ровным счетом ничего, вы с тем же успехом можете рассматривать «предельную таблицу» в которой все числа имеют бесконечное число разрядов, потому как она будет содержать все числа, котороые есть в каждой из «конечных таблиц». И, сюрприз-сюрприз, согласно аргументу Кантора, который вы так легко отвергли, найдется такое число, которого не будет в этой «предельной таблице».
3. Скорость роста на которую вы ссылаетесь никакого отношение к определеню счетности не имеет, соответсвенно скорость роста каких-то там функций ни на что не влияет.

mindtester
15.05.2018 10:49-11 — вы знакомы с деревом Штерна-Броко… после знакомства, сама попытка доказывать бесконечность множества рационалных на [0,1] кажется даже странной
2 — кстати (целая волна каментов выше) любое упоминание Pi в этом контексте не уместно — Pi изначально ирациональное
Aquahawk
15.05.2018 11:17Автор говорит о пересчёте всех действительных чисел указанного отрезка. Не только о рациональных, а о всех действительных. При этом вообще-то в первом курсе матана доказывается счётность множества рациональных чисел и несчётность множества действительных, с чем автор пытается спорить. И именно поэтому как самый простой пример который всё поломает приведено Pi. А раз автор говорит об отрезке [0,1] то и приводятся всякие Pi/4, Pi/5 и прочие 1/Pi, дабы не отвлекать сию превосходную дискуссию от самого главного.

izvolov
15.05.2018 23:17Правильно ли я понял, что вы считаете, что всё множество действительных чисел счётно?

FeRViD Автор
16.05.2018 08:42Не совсем. В конце поста я не зря добавил
P.S. Если предложенный мной алгоритм имеет ошибку, которую я, в силу своей невнимательности, не вижу – большая просьба написать об этом в комментариях.
P.P.S Если же ошибки нет – то получается, что |[0,1]| = |N|! Т.е. ВСЕ действительные числа из диапазона [0,1] можно пронумеровать!
Идея была вот в чем.
В множестве иррациональных чисел – любое число, например, Pi, v2, v3, e, Pi/n, e/n, v2/n, v3/n и т.д. — имеет бесконечное множество символов в записи, но это конкретное число, которое существует само по себе.
Чтобы получить все цифры в записи иррационального можно, например, воспользоваться методом приближения иррациональных чисел рациональными, но этот процесс будет бесконечным и мы никогда не получим все знаки в иррациональном числе, но при этом, это вполне конкретное число, существующее само по себе! Т.о. иррациональное число можно представить как бесконечно работающий алгоритм, который на каждой очередной итерации уточняет данное число, при этом процесс уточнения происходит бесконечно. Вопрос 1. Если нельзя, то почему?
В предложенном подходе порядковый номер любого числа N из [0,1] (обозначаемый как C(N)) есть функция от конкретных цифр его записи.
В такой интерпретации, порядковый номер иррационального числа становится таким же не определенным, как и все циры в записи самого иррационального числа. Порядковый номер иррационального будет вычисляться также бесконечно долго, как и все цифры в записи этого числа. Вопрос 2. Но, если доказано, что рациональные числа существуют сами по себе, тогда почему мы не можем утверждать, что при такой (алгоритмической) интерпретации их порядковые номера тоже существуют сами по себе?
Рассмотрим пример. Обозначим порядковый номер числа Pi/5 как C(Pi/5). С алгоритмической точки зрения, все знаки в записи числа Pi/5 будут утояняться бесконечно долго, => порядковый номер C(Pi/5) тоже будет вычисляться бесконечно долго.
izvolov
16.05.2018 09:59Переформирую вопрос.
Понятно ли, что отрезок[0, 1]и действительная прямаяRравномощны?
FeRViD Автор
16.05.2018 11:42Если открыть учебник по матану, то понятно.
1. Определение: континуум — мощность множества всех чисел из сегмента [0,1].
2. Теорема: множество континуума несчетно. Доказательство опирается на расмотренный выше диагональный метод Кантора.
3.… много разных определений, лемм, теорем…
4. Теорема Теорема Кантора — Бернштейна (упрощенно): если между множествами существует биекция, то |A| = |B|.
5. Устанавливаем биекцию между [0,1] и R, из чего, согласно (4) следует равномощность [0,1] и R.
Но, равномощность-то есть, однако несчетность — это пункт 2, а его доказательство опирается на диагональный метод Кантора, который, как я писал в статье вызывает у меня сомнения. Не могу объяснить, это на каком-то интуитивном уровне происходит.
Собственно, именно с целью прояснить этот момент (в первую очередь для себя), я и згорелся идей рассмотреть данный вопрос с другого ракурса, используя алгоритмический подход. Свои размышления я запостил на хабр с целью получить обратную связь от сообщества. Иногда так бывает, что самому трудно увидеть ошибку в своих же рассуждениях :-).
И, скорее всего, данный подход поможет (в первую очередь — мне) согласиться с правильностью диагонального метода Кантора. Т.к. у моего подхода уже вскрылось множество недостатков, за что спасибо всем, кто на все такие недостатки обратил внимание в комментариях.

anjensan
16.05.2018 11:34С алгоритмической точки зрения, все знаки в записи числа Pi/5 будут утояняться бесконечно долго, => порядковый ном уточняетер C(Pi/5) тоже будет вычисляться бесконечно долго.
Видите тут разницу? Уточняться vs вычисляться?
Уточняя некое число вы всегда можете остановиться и сказать «ну ок, мы получили число с заданной точностью. оно гарантированно лежит в таком-то диапазоне, ошибrа меньше чем некое конкретное число».
Т.о. иррациональное число можно представить как бесконечно работающий алгоритм, который на каждой очередной итерации уточняет данное число, при этом процесс уточнения происходит бесконечно.
Ну, можете и так формулировать, если хотите.
В такой интерпретации, порядковый номер иррационального числа становится таким же не определенным, как и все циры в записи самого иррационального числа. Порядковый номер иррационального будет вычисляться также бесконечно долго, как и все цифры в записи этого числа.
И тут уже «вычислятся» вместо «уточнятся». Айайай, как ловко (сарказм) вы поменяли одно на другое :)

FeRViD Автор
16.05.2018 11:47Согласен.
Я сейчас прихожу к мысли, что мой подход, наоборот, только еще раз показывает несчетность континуума, только с другой стороны. Пытаясь пронумеровать [0,1] способом, который я привел, мы просто получим бесконечное множество бесконечных алгоритмов, которые никогда не вычслят точный порядковый номер иррационального числа.
Aquahawk
16.05.2018 14:41Вооот, это уже похоже таки на понимание проблематики. Вообще с бесконечностями работа требует большой скурпулёзности. Например суммирование некоторых расходящихся рядов к наперёд заданному числу вас не смущает? Просто про расходящие ряды тут почитать можно neerc.ifmo.ru/wiki/index.php?title=Суммирование_расходящихся_рядов Или запихивание двумерной фигуры бесконечной площади внутрь трёхмерной фигуры конечного объёма? ru.wikipedia.org/wiki/Парадокс_маляра


Aquahawk
Проблема в том что не все действительные числа (и на самом деле большинство таких чисел) не представимы в виде конечной записи в двоичной и какой-бы то ни было другой системе счисления. Для числа 1/pi попробуйте вычислить его порядковый номер, его не существует (это будет число с бесконечным количеством знаков) в этом и проблема. А кантор доказывает равномощностность рациональных чисел и натуральных.