Приветствую всех и особенно тех кто интересуется задачами дискретной математики и теорией графов.
Предыстория
Так уж вышло, что ведомый интересом я занимался разработкой сервиса построения тур. маршрутов. Задача состояла в том, чтобы на основании интересующего пользователя города, категорий заведений и временных рамок спланировать оптимальные маршруты. Ну и одной из подзадач было рассчитывать время в пути от одного заведения до другого. Так как я был юн и глуп я решал эту задачу в лоб, алгоритмом Дейкстры, но справедливости ради стоит заметить, что только с ним можно было запустить итерацию из одного узла до тысяч других, кэшировать эти расстояния было не вариантом, заведений больше 10к только в одной Москве, а решения типа манхэттенского расстояния на наших городах не работает от слова совсем.
И так вышло, что проблему производительности в задаче комбинаторики решить удалось, а вот большую часть времени на обработку запроса отъедало поиск незакэшированных путей. Проблема усложнялась тем, что граф дорог Osm в Москве довольно большой (полмиллиона узлов и 1.1 млн дуг).
Не буду рассказывать про все потуги и что на самом деле проблему можно было бы решить обрезанием лишних дуг графа, расскажу лишь про то, что в какой-то момент меня озарило и я понял, что если подойти к алгоритму Дейкстры с точки зрения вероятностного подхода то он может быть линеен.
Дейкстра за логарифмическое время
Всем известно, а кому неизвестно почитайте, что алгоритм Дейкстры за счет использования очереди с логарифмической сложностью вставки и удаления можно привести к сложности вида O(nlog(n) + mlon(n)). При использовании фибоначчиевой кучи сложность можно опустить до O(n*lon(n) + m), но все равно не линейно, а хотелось бы.
В общем случае алгоритм с очередью описывается следующим образом:
Пусть:
- V — множество вершин графа
- E — множество ребер графа
- w[i, j] — вес ребра из узла i в узел j
- a — начальная вершина поиска
- q -очередь вершин
- d[i] — расстояние до i-го узла
- d[a] = 0, для всех остальных d[i] = +inf
Пока q не пустой:
- v — вершина с минимальным d[v] из q
- Для всех вершин u для которых есть переход в E из вершины v
- if d[u] > w[vu] + d[v]
- удалить u из q с расстоянием d[u]
- d[u] = w[vu] + d[v]
- добавить u в q с расстоянием d[u]
- if d[u] > w[vu] + d[v]
- удалить v из q
Если в качестве очереди использовать красно-черное дерево, где вставка и удаление происходят за log(n), а поиск минимального элемента аналогично за log(n), то сложность алгоритма составит O(nlog(n) + mlog(n)).
И тут стоит заметить одну важную особенность: ничего не мешает, в теории, рассмотреть вершину несколько раз. Если вершина была рассмотрена и расстояние до нее было обновлено на некорректное, большее, чем истинное значение, то при условии, что рано или поздно система сойдется и расстояние до u будет обновлено на корректное значение позволительно делать такие трюки. Но стоит заметить — одна вершина должна рассматриваться больше чем 1 раз с некоторой малой вероятностью.
Сортирующая хэш-таблица
Для сведения времени работы алгоритма Дейкстры к линейному предлагается структура данных, представляющая из себя хэш-таблицу с номерами узлов(node_id) в качестве значений. Замечу, потребность в массиве d никуда не девается, он все так же нужен, что получать расстояние до i-го узла за константное время.
На рисунке ниже приведен пример работы предлагаемой структуры.
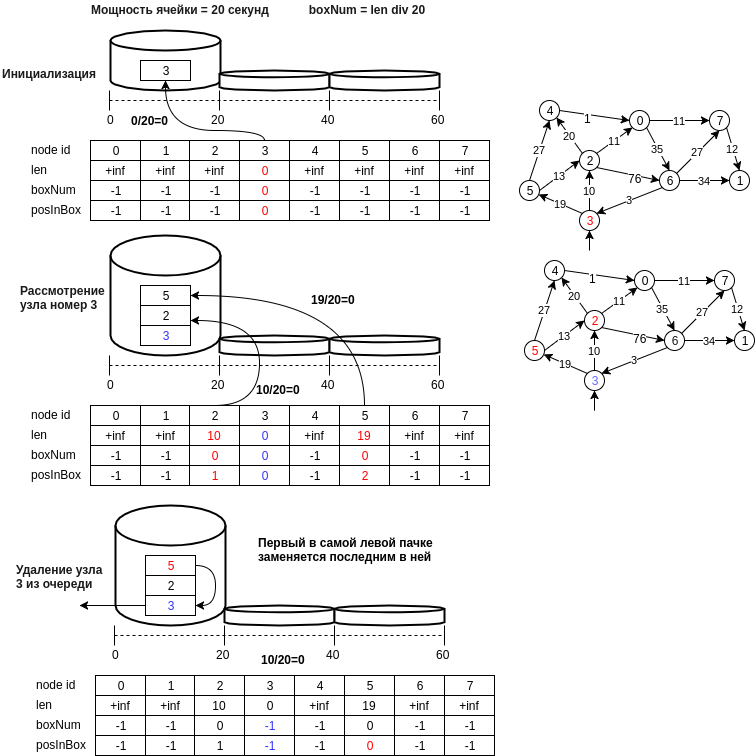
Опишем по шагам предложенную структуру данных:
- узел u записывается в ячейку под номером равным d[u] // bucket_size, где bucket_size мощность ячейки (к примеру 20 метров, т.е. ячейка под номером 0 будет содержать узлы расстояние до которых будет лежать в диапазоне [0, 20) метров)
- минимальным узлом будет считаться последний узел первой непустой ячейки, т.е. операция извлечения минимального элемента будет выполняться за O(1). Необходимо поддерживать актуальное состояние идентификатора номера первой непустой ячейки (min_el).
- операция вставки выполняется посредством добавления в конец ячейки нового номера узла и в тоже выполняется за O(1), т.к. вычисление номера ячейки происходит за константное время.
- операция удаления, как в случае с хэш-таблицей, возможен обычный перебор, и можно было бы сделать допущение и сказать, что при малом размере ячейки это тоже O(1). Если вам не жалко памяти (в принципе и не так много нужно, еще один массив на n), то можно завести массив позиций в ячейке. При этом, если удаляется элемент в середине ячейки, необходимо переместить последнее значение в ячейке на удаляемое место.
- важный момент при выборе минимального элемента: он является минимальным лишь с некоторой вероятностью, но, алгоримт будет просматривать ячейку min_el пока она не станет пустой и рано или поздно реальный минимальный элемент будет рассмотрен, и если мы случайно обновили некорректно значение расстояния до узла, достижимого из минимального, то смежные с минимальным узлы снова смогут окажутся в очереди и значение расстояния до них будет корректным и т.д.
- можно также удалять пустые ячейки до min_el, тем самым экономя память. В этом случае, удаление узла v из очереди q необходимо производить только после рассмотрения всех смежных узлов.
- а еще можно менять мощность ячейки, параметры увеличения размера ячейки и количества ячеек, когда нужно увеличить размер хэш-таблицы.
Результаты замеров
Проверки делались на карте osm Москвы, выгруженной через osm2po в postgres, а затем загруженной в память. Тесты писались на Java. Имелось 3 версии графа:
- исходный граф — 0.43 млн узлов, 1.14 млн дуг
- сжатая версия графа с 173k узлами и 750k дугами
- пешеходная версия сжатой версии графа, 450к дуг, 100к узлов.
Ниже приведен рисунок с замерами на разных версиях графа:

Рассмотрим зависимость вероятности повторного просмотра вершины и размера графа:
| кол-во просмотров узлов | кол-во вершин графа | вероятность повторного просмотра узла |
|---|---|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0.9 |
| 431490 | 419594 | 2.8 |
Можно заметить, что вероятность не зависит от размера графа и скорее специфична для запроса, но мала и ее диапазон конфигурируется посредством изменения мощности ячейки. Был бы очень благодарен за помощь в построении вероятностной модификации алгоритма с параметрами гарантирующими доверительный интервал в пределах, которого вероятность повторного просмотра не будет превышать некоторого процента.
Были проведены также качественные замеры для практического подтверждения сравнения корректности результата работы алгоритмы с новой структурой данных, показавшие полное совпадение длины кратчайшего пути от 1000 рандомных узлов до 1000 других рандомных узлов на графе. (и так 250 итераций) при работе с сортирующей хэш-таблицей и красно-черным деревом.
Исходный код предложенной структуры данных лежит по ссылке
P.S.: Про алгоритм Торупа и то, что он решает эту же задачу тоже за линейное время знаю, но я не смог осилить этот фундаментальный труд за один вечер, хотя и понял в общих чертах идею. По крайней мере, как я понял, там предлагается другой подход, основанный на построении минимального остовного дерева.
P.S.S. В течении недели постараюсь найти время и провести сравнение с фибоначчиевой кучей и чуть позже дополнить github репу примерами и кодами тестов.
Комментарии (5)

nobodyhave
05.07.2018 13:49Можете еще посмотреть на Radix heap. Там тоже корзины и все такое, а в реализации ИМХО попроще чем куча Фибоначчи.


yeputons
Как проверялась корректность реализации? Например, верно ли, что ответы двух реализаций (стандартной и с корзинами) совпали на всех вершинах графа при поиске расстояний от фиксированной вершины `V`?
Не пробовали ли вы в каждой ячейке воспользоваться обычной кучей (например, для Java это `PriorityQueue`) вместо массива?
Есть ли какой-то смысл в написании своей реализации `BitArray` и частичной реализации `ArrayList` внутри `NewSortedHashMapEntry`?
А каковы длины дуг? Например, если длина дуги всегда больше, чем размер корзины, то можно отсортировать каждую корзину перед её первым посещением и появится гарантия, что каждая вершина посещается не больше одного раза. Ну или можно просто отсортировать и посмотреть, что будет. Или сделать `Collections.shuffle` перед первым проходом.
Junkers Автор
Корректность проверялась путем проверки полного совпадения массива d расстояний.
Нет, но прелесть массива примитивов в скорости его работы. Тут скорее имеет смысл сравнить с бинарной кучей, к примеру.
Да, интересно было попробовать реализовать битовую маску применяя сравнение без ifов. Вполне вероятно, что можно применить и готовые библиотеки.
По поводу длины дуг, большое спасибо, очень интересное дополнение, попробую обязательно реализовать и дополню статью.
yeputons
Да, неточно выразился, бинарная куча (binary heap) и подразумевалась. Это получится этакая оптимизация стандартного алгоритма с двоичной кучей, просто в которой куча разделена на несколько корзин. Мне кажется, чем-то напоминает radix sort.
Не очень понял, что вы подразумеваете под "сравнением без if'ов". Можете пояснить? Я не понимаю, чем ваша реализация принципиально лучше массива boolean, кроме того, что может занимать меньше места. А вообще в Java есть встроенный битовый массив —
BitSet.yeputons
В статье написано, что проверялись только расстояния до случайной тысячи узлов и её хорошо бы исправить или я чего-то не понимаю?