Главная
Автоматическая реорганизация массивов в памяти графического ускорителя

Автоматическая реорганизация массивов в памяти графического ускорителя +9

07.07.2015 19:00

ALEX_k_s 0 4003 Источник

О чем речь

В данном посте я бы хотел описать часть системы времени выполнения (RTS — RunTime System в дальнейшем) компилятора DVMH. Рассматриваемая часть, как видно из заголовка, относится к обработке пользовательских массивов на GPU, а именно, их автоматическая трансформация или реорганизация в памяти ускорителя. Данные преобразования делаются для эффективного доступа к памяти GPU в вычислительных циклах. Что такое DVMH, как можно подстраиваться под вычисления и почему это делается автоматически — описано далее.

Что такое DVMH

Так как данный пост посвящен обзору алгоритмов преобразования массивов, то опишу лишь вкратце что такое DVMH, так как это понадобится для описания принципов работы. Начинать надо с системы DVM (Distribute virtual memory) — с системы, которая предназначается для разработки программ для кластеров, содержащих в узлах ускорители (GPU Nvidia и Intel Xeon Phi) и многоядерные процессоры. С помощью данной системы можно легко распараллеливать большие последовательные программы, работающие в первую очередь со структурными сетками или структурными типами данных, а также легко отобразить программу на кластер, в узлах которого могут быть устройства разной архитектуры. DVM-система включается в себя:

Компиляторы с языков программирования Си (а в будущем и С++, конечно же с некоторыми ограничениями) и Фортрана — С-DVMH и Fortran-DVMH. Будем называть обобщенно языками и компиляторами DVMH. DVMH представляет собой расширение рассматриваемых языков программирования прагмами или спецкомментариями, которые не видны стандартным компиляторам (по аналогии, например, с OpenMP, OpenACC). Тем самым программисту достаточно расставить небольшое количество директив, указывающих как распределены данные и как отображены вычисления на распределенные данные в вычислительных циклах. После этого, пользователь получает как последовательную программу, так и параллельную. Полученную программу можно выполнять на кластере на разном количестве узлов, на одном или нескольких GPU в рамках одного узла, а также, например, задействовать многоядерные процессоры, графические ускорители и ускорители Intel Xeon Phi сразу (если все это присутствует на рассматриваемом сервере). Более подробно можно ознакомиться тут;
Библиотека поддержки Lib-DVMH или система времени выполнения RTSH (H означает heterogeneous, данная буква в названии многих компонент появилась после того, как система была расширена для поддержки GPU и Xeon Phi). С помощью данной системы осуществляется вся настройка программы пользователя во время работы программы;
Средства отладки и средства отладки эффективности DVMH программ (пока только для Fortran-DVMH программ).

Основной целью создания такой системы — упростить пользователю жизнь по распараллеливанию уже существующих программ и упростить написание новых параллельных программ. DVMH-компиляторы транслируют получившуюся программу с директивами DVMH в программу с использованием MPI, OpenMP и CUDA и вызовами RTSH. Тем самым пользовательская программа с помощью директив распределения вычислений (практически аналогичных OpenMP или OpenACC) и директив распределения данных может быть легко распараллелена. Причем данная программа продолжает быть последовательной, что не мало важно для ее дальнейшей разработки и поддержки. Написать «хорошую» последовательную программу и расставить в такой программе директивы DVMH-компилятору все же проще, чем заниматься распаралелливанием вручную.

Уровни параллелизма

После небольшого вступления и введения в курс дела, рассмотрим, а как вообще происходит отображение исходной программы (а именно вычислительных циклов) на разные уровни параллелизма внутри RTSH. В настоящее время чтобы достичь большой вычислительной мощности, используют большое количество потоков в рамках одного устройства, вместо роста частоты работы каждого из потоков. Это приводит в свою очередь к потребности в изучении не только стандарта (MPI конечно же) взаимодействия процессов между узлами, но и к появлению разнородных архитектур, а вместе с ними и различных параллельных языков, как высокого уровня, так и низкого. И все это осложняет жизнь конечному пользователю. И чтобы достичь высокой производительности приложений, необходимо использовать все возможности конкретного вычислительного кластера.

На данный момент можно представить себе два уровня параллелизма — между узлами и внутри узла. Внутри узла могут использоваться один или несколько GPU, а также многоядерные процессоры. Intel Xeon Phi в данной схеме рассматривается как отдельный узел, содержащий в себе многоядерный процессор. Ниже приведена обобщенная схема вычислительного кластера, на который могут отображаться DVMH-программы:

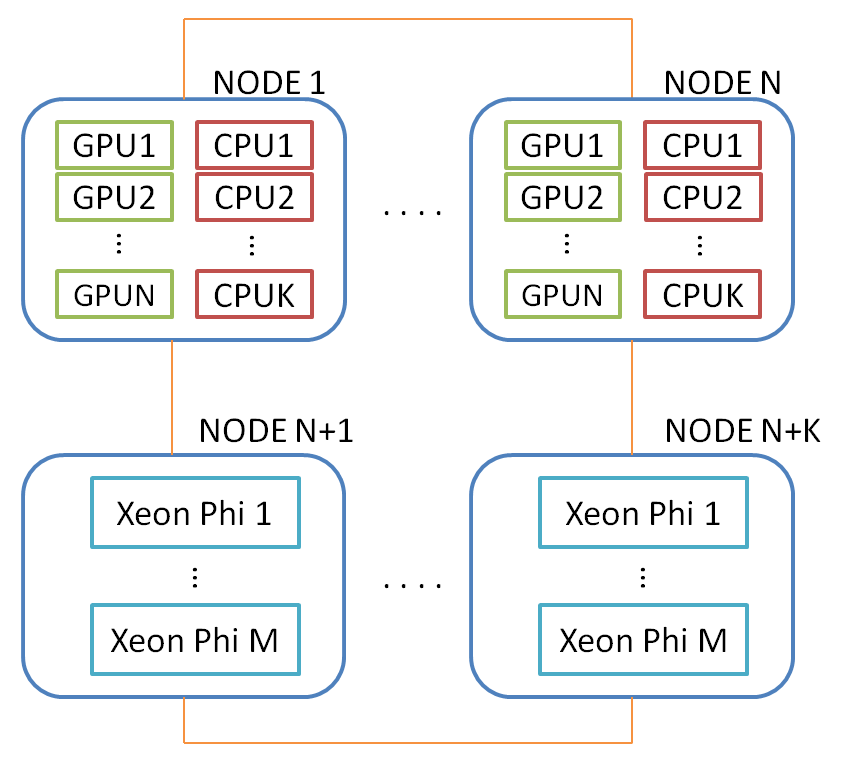
Естественно возникает вопрос балансировки загрузки устройств (механизм которой есть в DVMH), но это уже за рамками данного поста. Все дальнейшие рассмотрения будут затрагивать один GPU в рамках одного узла. Описанные далее преобразования выполняются на всех GPU, на которых происходит работа DVMH-программы, независимо.

Для чего нужна реорганизация данных

Наконец, после затяжного вступления, мы подошли к вопросу самой реорганизации. Для чего же это все нужно? А вот для чего. Рассмотрим какой нибудь вычислительный цикл:

 double ARRAY[Z][Y][X][5];

 for(int I = 1; i < Z; ++I)
   for(int J = 1; J < Y; ++J)
     for(int K = 1; K < X; ++K) 
       ARRAY[K][J][I][4] = Func(ARRAY[K][J][I][2], ARRAY[K][J][I][5]);

У нас есть четырехмерный массив, где первое (самое быстрое) измерение, например, содержит 5 физических величин, а остальные — являются координатами в пространстве расчетной области. В программе массив был объявлен так, что первое (близко расположенное в памяти) измерение состоит из этих 5 элементов, чтобы в вычислительных циклах кэш процессора работал хорошо. В данном примере необходим доступ ко 2, 4 и 5 элементам быстрого измерения на каждой итерации трех циклов. Также стоит отметить, что цикла по этому измерению нет. И в силу, например, разной природы этих величин, будут отличаться и вычисления по каждому из 5ти элементов.

Тем самым можно параллельно выполнить циклы по I, J, K. Для данного примера каждый элемент массива ARRAY будет каким то образом отображен на параллельный цикл, например, так:

#pragma dvm array distribute[block][block][block][*]
 double ARRAY[Z][Y][X][5];

#pragma dvm parallel([I][J][K] on ARRAY[I][J][K][*])
 for(int I = 1; i < Z; ++I)
   for(int J = 1; J < Y; ++J)
     for(int K = 1; K < X; ++K) 
       ARRAY[K][J][I][4] = Func(ARRAY[K][J][I][2], ARRAY[K][J][I][5]);

То есть появляется распределение данных, относительно которого распределяются вычисления. Приведенные выше директивы DVMH говорят о том, что надо распределить массив по трем измерениям равными блоками, а четвертое (самое быстрое) размножить. Данная запись позволяет отобразить массив на процессорную решетку, заданную при запуске DVMH-программы. Следующая директива говорит о том, что надо выполнять виток (I,J,K) в соответствии правилу распределения массива ARRAY. Тем самым директива PARALLEL задает отображение витков цикла на элементы массива. Во время выполнения RTSH знает как расположены массивы и как надо организовывать вычисления.

Данный цикл, а именно все пространство витков, может отображаться как на нити OpenMP, так и на CUDA-нити, потому что все три цикла не имеют никаких зависимостей. Нас интересует отображение на CUDA архитектуру. Всем известно, что CUDA-блок содержит три измерения — x,y,z. Самое первое является самым быстрым. Быстрое измерение отображается на warp'ы CUDA-блока. Зачем все это нужно упоминать? Затем, что глобальная память GPU (GDDR5) является узким местом в любых вычислениях. И память устроена таким образом, что наиболее быстрый доступ осуществляется одним warp'ом только в том случае, если все загружаемые элементы лежат подряд. Для приведенного выше цикла существует 6 вариантов отображения пространства витков (I,J,K) на CUDA-блок (x, y, z), но ни один из них не позволяет эффективно обращается к массиву ARRAY.

От чего же это возникает? Если посмотреть описание массива, то видно, что первое измерение содержит 5 элементов и по нему нет цикла. Тем самым элементы второго быстрого измерения лежат на расстоянии в 40 байт (5 элементов типа double), что приводит к увеличению количества транзакций к памяти GPU (вместо 1 транзакции один warp может сделать до 32х транзакций). Все это ведет к перегрузке шины памяти и снижению производительности.

Чтобы решить проблему, в данном случае достаточно поменять местами первое и второе измерение, то есть выполнить транспонирование двухмерной матрицы размером X*5 Y*Z раз или выполнить Y*Z независимых транспонирований. Но что значит поменять местами измерения массива? Могут возникать следующие проблемы:

Необходимо дописывать в код дополнительные циклы, которые выполняют данное преобразование;
Если переставлять измерения в коде программы, то придется исправлять всю программу, так как вычисления во всех циклах станут не корректными, если в одной точке программы переставить измерения массива. А если программа большая, то можно наделать много ошибок;
Не ясно какой эффект от перестановки будет получен и как перестановка отразится на другом цикле. Вполне возможно потребуется новая перестановка или возврат массива в исходное состояние;
Создавать две версии программы, так как данный цикл перестанет эффективно выполняться на CPU.

Реализация различных перестановок в RTSH

Для решения описанных проблем в RTSH был придуман механизм автоматической трансформации массивов, который позволяет существенно ускорить DVMH-программу пользователя (в несколько раз) в случае неудачного обращения к памяти GPU (по сравнению с ее выполнением без применения данной возможности). Перед рассмотрением типов трансформации и их реализации на CUDA, перечислю некоторые неоспоримые плюсы нашего подхода:

Пользователь имеет одну DVMH-программу, он сосредотачивается на написании алгоритма;
Данный режим может быть включен во время компиляции DVMH-программы указанием всего лишь одной опции DVMH компилятору -autoTfm. Тем самым пользователь без всяких изменений программы может попробовать оба режима и оценить ускорение;
Данная трансформация выполняется в режиме «по требованию». Это означает, что в случае изменения порядка измерений массива перед вычислительным циклом, обратная перестановка после вычислений выполняться не будет, так как, вполне возможно, для следующего цикла данное расположение массива будет выгодным;
Существенное ускорение программы (до 6 раз) по сравнению с той же самой программой, выполненной без применения данной опции.

1. Поменять местами измерения массива, являющиеся физически соседними.

Описанный выше пример подходит под данный тип преобразования. В данном случае, необходимо выполнить транспонирование двухмерной плоскости, которая может располагаться на любых соседних двух измерениях массива. Если необходимо транспонировать первые два измерения, то здесь подходит хорошо описанный алгоритм транспонирования матрицы с применением разделяемой памяти:

__shared__ T temp[BLOCK_DIM][BLOCK_DIM + 1];

CudaSizeType x1Index = (blockIdx.x + pX) * blockDim.x + threadIdx.x;
CudaSizeType y1Index = (blockIdx.y + pY) * blockDim.y + threadIdx.y;
CudaSizeType x2Index = (blockIdx.y + pY) * blockDim.y + threadIdx.x;
CudaSizeType y2Index = (blockIdx.x + pX) * blockDim.x + threadIdx.y;
CudaSizeType zIndex = blockIdx.z + pZ;

CudaSizeType zAdd = zIndex * dimX * dimY;
CudaSizeType idx1 = x1Index + y1Index * dimX + zAdd;
CudaSizeType idx2 = x2Index + y2Index * dimY + zAdd;

if ((x1Index < dimX) && (y1Index < dimY)) {
    temp[threadIdx.y][threadIdx.x] = inputMatrix[idx1];
}
__syncthreads();
if ((x2Index < dimY) && (y2Index < dimX)) {
    outputMatrix[idx2] = temp[threadIdx.x][threadIdx.y];
}

В случае квадратной матрицы, можно выполнять транспонирование так называемое «in place», для которого не нужно выделять дополнительную память на GPU.

2. Поменять местами измерения массива, не являющиеся физически соседними.

К данному типу относятся перестановки любых двух измерений массива. Стоит выделить два вида таких перестановок: первый — поменять любое измерение с первым и поменять любые измерения между собой, причем ни одно не является первым (самым быстрым). Данное разделение должно быть понятным, так как элементы самого быстрого измерения лежат подряд и доступ к ним должен быть также по возможности подряд. Для этого можно воспользоваться разделяемой памятью:

__shared__ T temp[BLOCK_DIM][BLOCK_DIM + 1];

CudaSizeType x1Index = (blockIdx.x + pX) * blockDim.x + threadIdx.x;
CudaSizeType y1Index = (blockIdx.y + pY) * blockDim.y + threadIdx.y;
CudaSizeType x2Index = (blockIdx.y + pY) * blockDim.y + threadIdx.x;
CudaSizeType y2Index = (blockIdx.x + pX) * blockDim.x + threadIdx.y;
CudaSizeType zIndex = blockIdx.z + pZ;
CudaSizeType zAdd = zIndex * dimX * dimB * dimY;
CudaSizeType idx1 = x1Index + y1Index * dimX * dimB + zAdd;
CudaSizeType idx2 = x2Index + y2Index * dimY * dimB + zAdd;

for (CudaSizeType k = 0; k < dimB; k++) {
    if (k > 0)
        __syncthreads();
    if ((x1Index < dimX) && (y1Index < dimY)) {
        temp[threadIdx.y][threadIdx.x] = inputMatrix[idx1 + k * dimX];
    }
    __syncthreads();
    if ((x2Index < dimY) && (y2Index < dimX)) {
        outputMatrix[idx2 + k * dimY] = temp[threadIdx.x][threadIdx.y];
    }
}

Если же нужно выполнить перестановку любых других измерений между собой, то разделяемая память не нужна, так как доступ к быстрому измерению массива будет выполняться «правильно» (соседние нити будут работать с соседними ячейками в памяти GPU).

3. Выполнить диагонализацию массива.

Данный вид перестановки является нестандартным и является необходимым для параллельного выполнения циклов с регулярной зависимостью по данным. Данная перестановка обеспечивает «правильный» доступ при обработке цикла, в котором есть зависимости. Рассмотрим пример такого цикла:

#pragma dvm parallel([ii][j][i] on A[i][j][ii]) across(A[1:1][1:1][1:1])
    for (ii = 1; ii < K - 1; ii++)
        for (j = 1; j < M - 1; j++)
            for (i = 1; i < N - 1; i++)
                A[i][j][ii] = A[i + 1][j][ii] + A[i][j + 1][ii] + A[i][j][ii + 1] + A[i - 1][j][ii] + A[i][j - 1][ii] +  A[i][j][ii - 1];

В данном случае есть зависимость по всем трем измерениям цикла или трем измерениями массива А. Для того, чтобы сообщить DVMH-компилятору, что в данном цикле есть регулярная зависимость (зависимые элементы могут быть выражены формулой a*x + b, где а и b — константы), существует спецификация ACROSS. В данном цикле есть прямая и обратная зависимости. Пространство витков данного цикла образуют параллелепипед (и в частном случае — трехмерный куб). Плоскости данного параллелепипеда, повернутые под 45 градусов относительно каждой грани, можно выполнять параллельно, в то время как сами плоскости — последовательно. Из-за этого и появляется доступ к дигональным элементам первых двух самых быстрых измерений массива А. И для увеличения производительности GPU, необходимо выполнить диагональную трансформацию массива. В простом случае преобразование одной плоскости выглядит так:

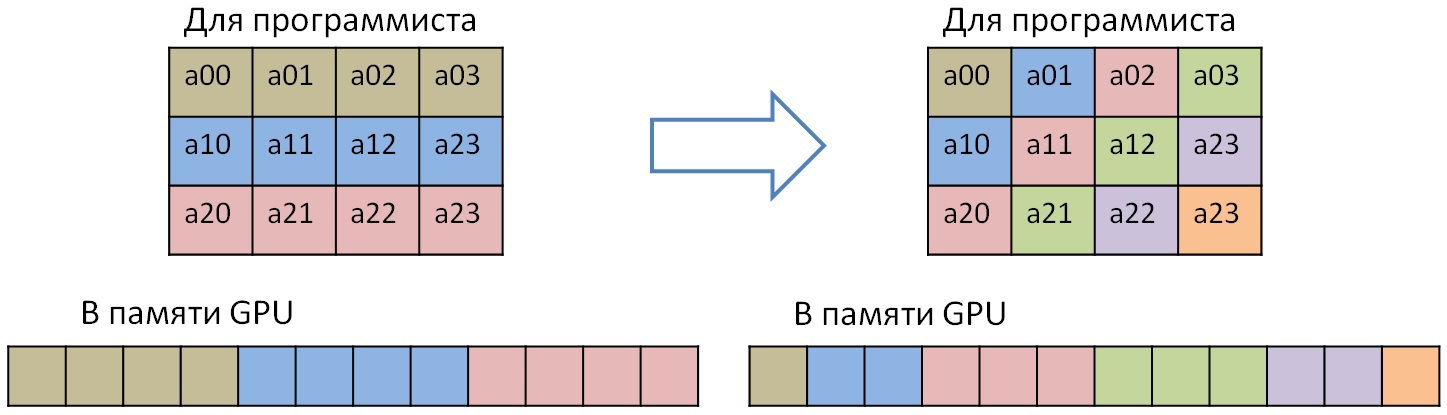
Выполнить данное преобразование можно также быстро, как и транспонирование матрицы. Для этого необходимо использовать разделяемую память. Только в отличие от транспонирования матрицы, обрабатываемый блок будет не квадратным, а в виде параллелограмма, чтобы при чтении и записи эффективно использовать пропускную способность памяти GPU (для диагонализации показана только первая полоса, так как все остальные — разбиваются аналогично):

Реализованы следующие виды диагонализации (Rx и Ry — размеры диагонализируемого прямоугольника):

Параллельно побочной диагонали и Rx == Ry;
Параллельно побочной диагонали и Rx < Ry;
Параллельно побочной диагонали и Rx > Ry;
Параллельно главной диагонали и Rx == Ry;
Параллельно главной диагонали и Rx < Ry;
Параллельно главной диагонали и Rx > Ry.

Общее ядро для диагонализации выглядит следующим образом:

__shared__ T data[BLOCK_DIM][BLOCK_DIM + 1];
__shared__ IndexType sharedIdx[BLOCK_DIM][BLOCK_DIM + 1];
__shared__ bool conditions[BLOCK_DIM][BLOCK_DIM + 1];
bool condition;

IndexType shift;
int revX, revY;
if (slash == 0) {
    shift = -threadIdx.y;
    revX = BLOCK_DIM - 1 - threadIdx.x;
    revY = BLOCK_DIM - 1 - threadIdx.y;
} else {
    shift = threadIdx.y - BLOCK_DIM;
    revX = threadIdx.x;
    revY = threadIdx.y;
}

IndexType x = (IndexType)blockIdx.x * blockDim.x + threadIdx.x + shift;
IndexType y = (IndexType)blockIdx.y * blockDim.y + threadIdx.y;
IndexType z = (IndexType)blockIdx.z * blockDim.z + threadIdx.z;

dvmh_convert_XY<IndexType, slash, cmp_X_Y>(x, y, Rx, Ry, sharedIdx[threadIdx.y][threadIdx.x]);
condition = (0 <= x && 0 <= y && x < Rx && y < Ry);
conditions[threadIdx.y][threadIdx.x] = condition;
if (back == 1)
    __syncthreads();

#pragma unroll
for (int zz = z; zz < z + manyZ; ++zz) {
    IndexType normIdx = x + Rx * (y + Ry * zz);

    if (back == 0) {
        if (condition && zz < Rz)
            data[threadIdx.y][threadIdx.x] = src[normIdx];
        __syncthreads();
        if (conditions[revX][revY] && zz < Rz)
            dst[sharedIdx[revX][revY] + zz * Rx * Ry] = data[revX][revY];
    } else {
        if (conditions[revX][revY] && zz < Rz)
            data[revX][revY] = src[sharedIdx[revX][revY] + zz * Rx * Ry];
        __syncthreads();
        if (condition && zz < Rz)
            dst[normIdx] = data[threadIdx.y][threadIdx.x];
    }
}

В данном случае необходимо передавать значение условия и вычисленную координату в диагональном представлении с помощью dvmh_convert_XY другим нитям, потому что в отличие от транспонирования, здесь не получается однозначно вычислить обе координаты (откуда считывать и куда записывать).

Итог. Какие перестановки реализованы:

Перестановка двух соседних измерений массива;
Перестановка двух не соседних измерений массива;
Дигонализация двух соседних самых быстрых измерений массива;
[Планируется] Дигонализация двух любых самых быстрых измерений массива (диагонализируемое измерение становится самым быстрым);
Копирование вырезки из диагонализируемого массива (например для обновления «теневых» граней в случае счета на нескольких GPU);

Оценка производительности

Для демонстрации эффективности подхода приведу некоторые графики, показывающие производительность самих перестановок и приведу результаты выполнения двух программ — LU разложение для задачи газо-гидродинамики и синтетический тест, реализующий метод последовательной верхней релаксации решения 3-мерной задачи Дирихле. Все тесты запускались на GPU GTX Titan и Nvidia CUDA ToolKit 7.0 и процессоре Intel Xeon E5 1660 v2 с Intel компилятором 15й версии.

Будем сравнивать все реализованные преобразования с ядром обычного копирования, так как реорганизация массивов — это копирование одного участка памяти в другой по определенному правилу. Ядро копирования выглядит так:

__global__ void copyGPU(const double *src, double *dist, unsigned elems)
{
	unsigned idx = blockIdx.x * blockDim.x + threadIdx.x;
	if(idx < elems)
		dist[idx] = src[idx];
}

Приведу скорость преобразования только для алгоритмов, использующих разделяемую память, так как в данном случае присутствуют дополнительные накладные расходы на синхронизацию внутри CUDA-блока, а также на доступ к разделяемой памяти (кэшу L1), из-за чего производительность такого копирования будет ниже, чем при любых других перестановках. За 100% возьмем скорость ядра копирования copyGPU, так как в данном случае накладные расходы минимальны и данное ядро позволяет получить почти пиковую пропускную способность памяти GPU.

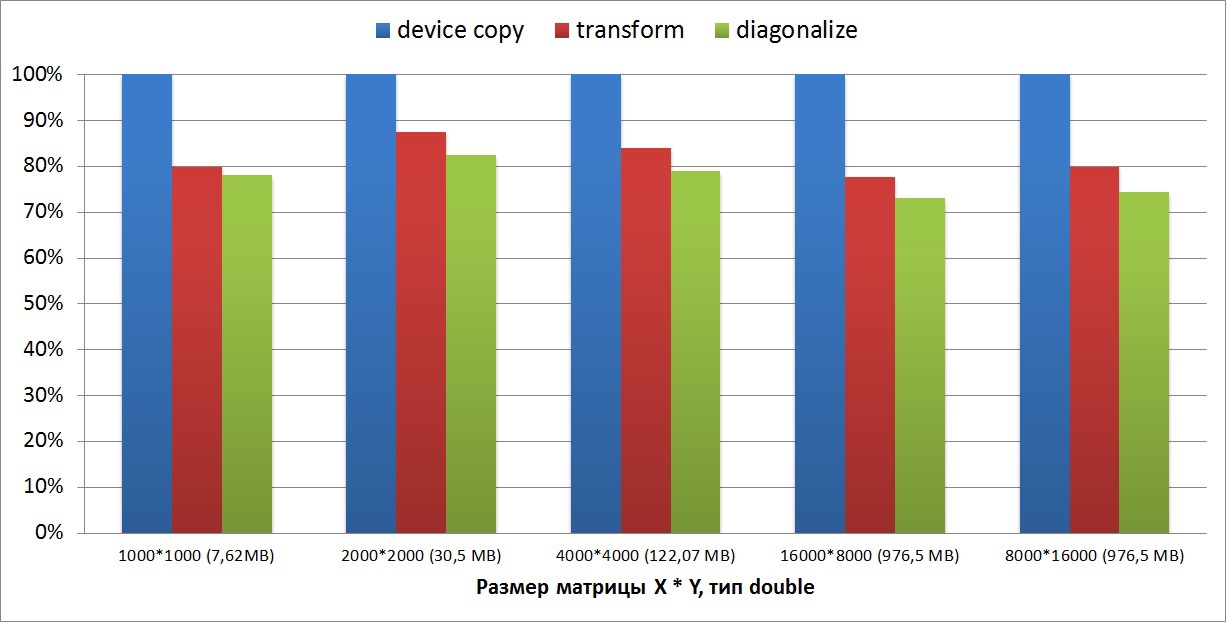
Первый график показывает на сколько медленнее выполнялись трансформация (транспонирование) и диагонализация двухмерной матрицы. Размер матриц варьируется от нескольких мегабайт до одного гигабайта. Из графика видно, что на двухмерных матрицах падение производительности составляет 20-25% по отношению к ядру copyGPU. Также видно, что диагонализация выполняется на 5% дольше, так как алгоритм диагонализации несколько сложнее транспонирования матрицы:

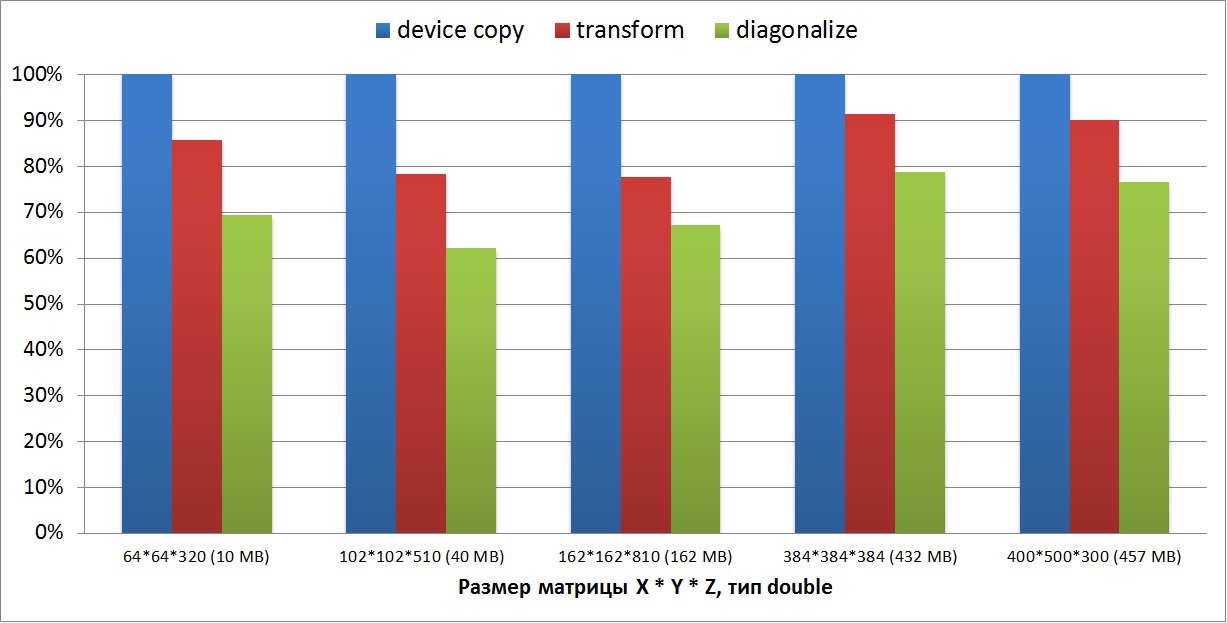
Второй график показывает на сколько медленнее выполнялись трансформация (транспонирование) и диагонализация трехмерной матрицы. Размеры матриц брались двух типов: четырехмерные вида N*N*N*5 и произвольные X*Y*Z. Размеры матриц варьируются от 10 мегабайт до 500 мегабайт. На маленьких матрицах скорость преобразований падает на 40%, в то время как на больших матрицах скорость трансформации достигает 90%, а скорость диагонализации — 80% от скорости копирования:

Третий график показывает время выполнения синтетического теста, реализующего метод симметричной верхней релаксации. Вычислительный цикл данного метода содержит зависимости по всем трем измерениям (данный цикл на языке Си описан выше). На графике приведены времена выполнения одной и той же DVMH-программы (написанной на Фортране, исходный код прикреплен в конце статьи), с использованием 6ти нитей Xeon E5 и на GPU с применением диагонализации и без. В данном случае диагонализацию необходимо сделать всего один раз до итеративных вычислений.

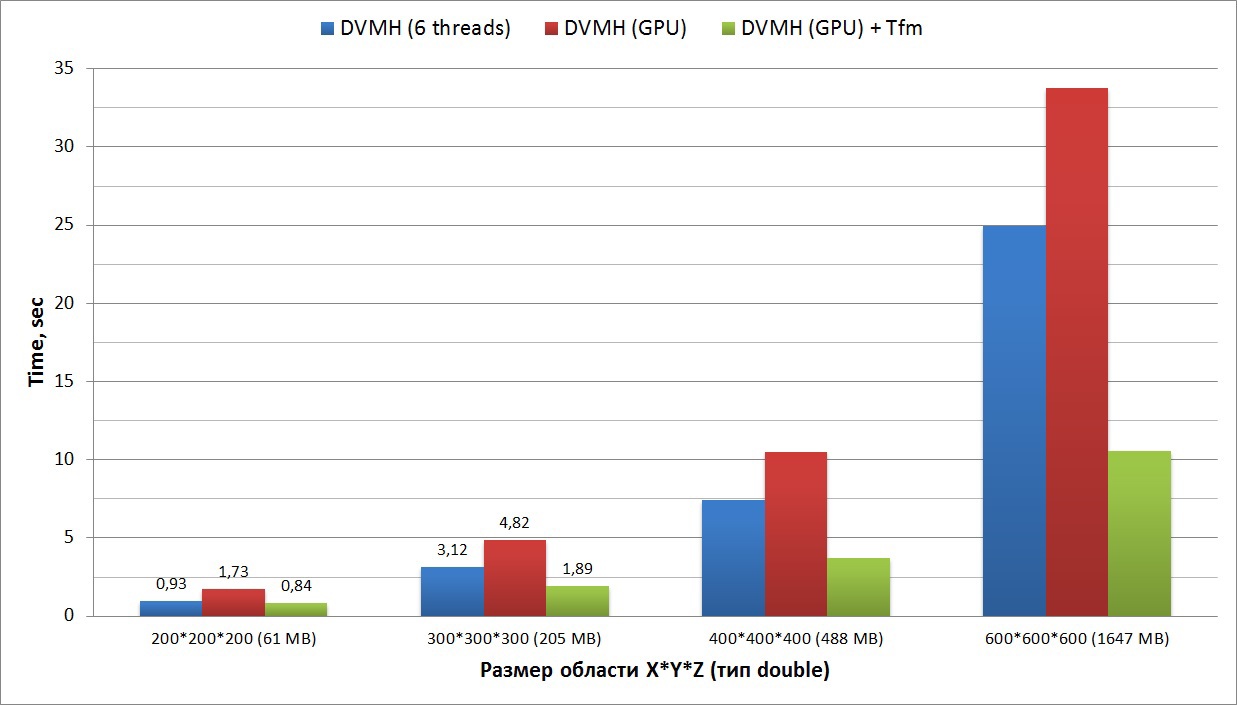
Четвертый график показывает ускорение приложения, решающего синтетическую систему нелинейных дифференциальных уравнений в частных производных (3-х мерная система уравнений Навье-Стокса для сжимаемой жидкости или газа), используя метод симметричной последовательной верхней релаксации (алгоритм SSOR, задача LU). Данный тест входит в стандартный пакет тестов NASA (последняя доступная версия 3.3.1). В данном наборе доступны исходные коды всех тестов последовательных версий, а также MPI и OpenMP.

На графике приведены ускорения программы по отношению к последовательной версии, выполненной на одном ядре Xeon E5, выполненной на 6ти нитях Xeon E5, и на GPU в двух режимах. В данной программе необходимо делать диагонализацию только для двух циклов, а далее возвращать массив в исходное состояние, то есть на каждой итерации для «плохих» циклов происходит диагонализация всех требуемых массивов, а после выполнения происходит из раздиагонализация. Также стоит отметить, что в данной программе порядка 2500 тыс строк стиля Фортран 90 (без переносов, код в конце статьи прикреплен). В нее добавлено 125 DVMH-директив, которые позволяют выполнять данную программу как на кластере, на одном узле на разных устройствах, так и в последовательном режиме.

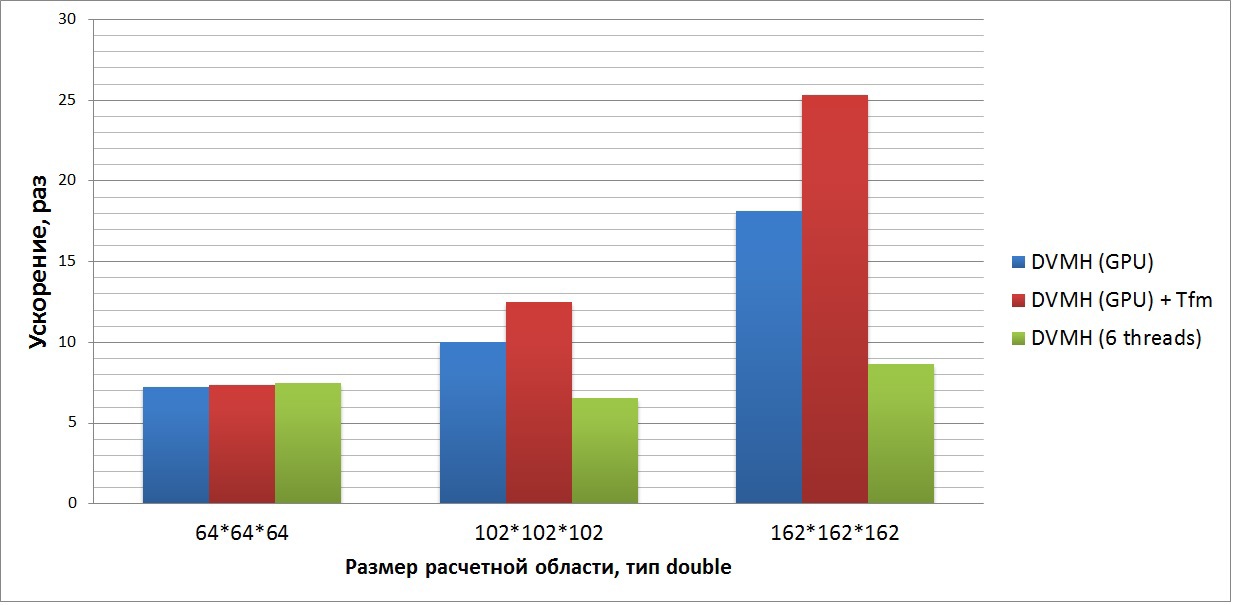
Данная программа хорошо оптимизирована на уровне последовательного кода (это видно по 8ми кратному ускорению на 6ти ядрах Xeon E5), который хорошо отображается не только на GPU архитектуру, но и на многоядерные процессоры. DVMH-компилятор позволяет по опции -Minfo посмотреть количество регистров, необходимых CUDA-ядрам, соответствующим каждому отображаемому циклу (данная информация берется от компилятора Nvidia). В данном случае необходимо порядка 160 регистров на одну нить (из 255 доступных) для каждого из трех основных вычислительных циклов, а количество операций на обращение к глобальной памяти равно примерно 10:1. Тем самым ускорение от использования реорганизации не такое большое, но оно все равно есть и на большой задаче составляет 1,5 раза по сравнению с той же программой, выполненной без этой опции. Также данный тест выполняется быстрее в 3 раза на GPU, чем на 6ти ядрах CPU.

Заключение

В данном посте был рассмотрен подход автоматической реорганизации данных на GPU в системе поддержки выполнения DVMH-программ. В данном случае речь идет о полной автоматизации данного процесса. RTSH обладает всей информацией во время выполнения программы, необходимой для определения типа реорганизации. Данный подход позволяет получить хорошее ускорение на тех программах, где не удается написать «хорошую» последовательную программу, при отображении циклов которой доступ к глобальной памяти GPU осуществлялся наилучшим образом. При выполнении трансформаций достигается до 90% производительности глобальной памяти GPU (что составляет примерно 240 GB/s для GTX Titan) относительно самого быстрого ядра копирования памяти внутри устройства.

Ссылки

1) DVM-система
2) Исходный код LU и SOR на Fotran-DVMH
3) Тесты NASA