Этот текст написан для тех, кто интересуется глубоким обучением, кто хочет использовать разные методы библиотек pytorch и tensorflow для минимизации функции многих переменных, кому интересно научиться превращать последовательно выполняющуюся программу в выполняемые с помощью numpy векторизованные матричные вычисления. А ещё можно научиться делать мультфильм из данных, визуализированных с помощью PovRay и vapory.
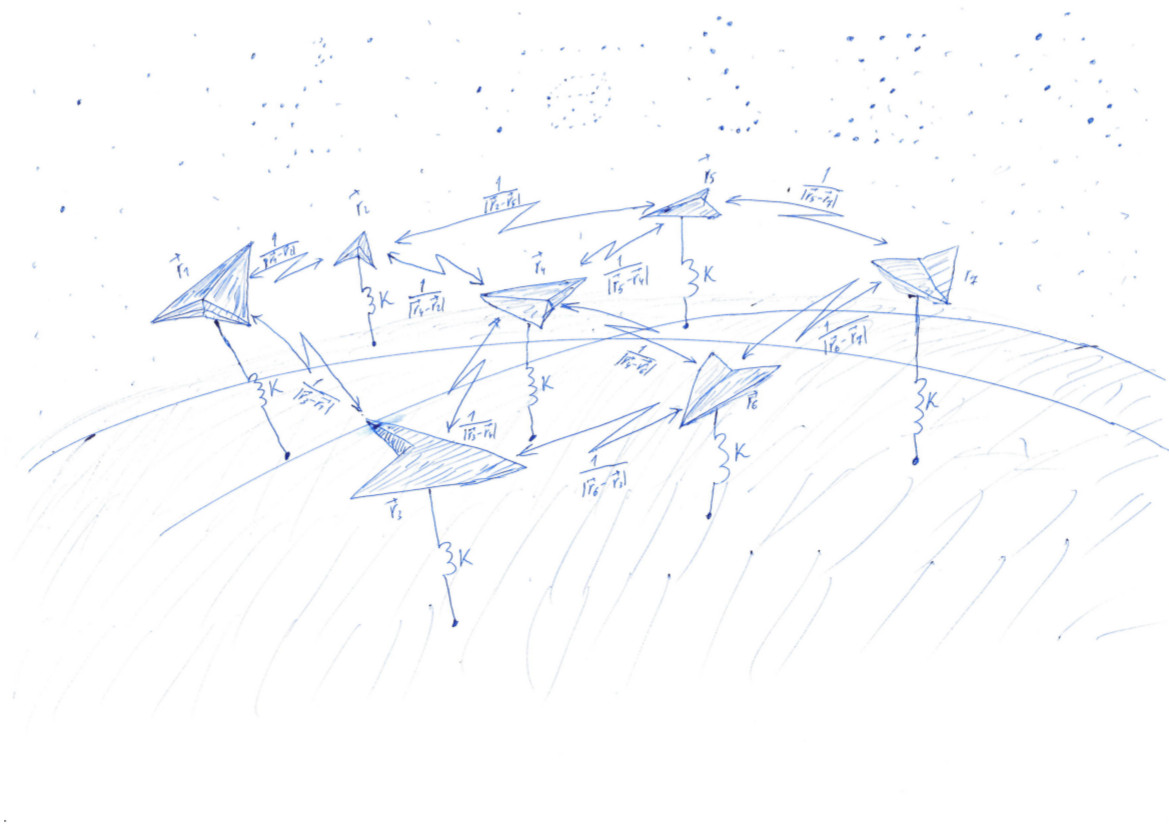
Откуда задача
Каждый минимизирует свой функционал (с) Анонимный дата-сайентист
В одной из предыдущих публикаций нашего блога, а именно в пункте "Грабли №6", рассказывалось о технологии DSSM, которая позволяет преобразовать текст в векторы. Чтобы найти такое отображение, нужно найти коэффициенты линейных преобразований, минимизирующих довольно сложную функцию потерь. Понять, что происходит при обучении такой модели, тяжело из-за большой размерности векторов. Чтобы выработать интуицию, позволяющую правильно выбрать метод оптимизации и задать параметры этого метода, можно рассмотреть упрощённый вариант этой задачи. Пусть теперь вектора находятся в нашем обычном трёхмерном пространстве, тогда их легко нарисовать. А функция потерь будет потенциалом отталкивания точек друг от друга и притяжения к единичной сфере. В этом случае решением задачи будет равномерное распределение точек по сфере. Качество текущего решения легко оценить на глаз.
Итак, будем искать равномерное распределение по сфере заданного количества точек. Такое распределение бывает нужно акустику для того, чтобы понять, в каком направлении запустить волну в кристалле. Связисту — чтобы узнать, как расположить на орбите спутники для достижения наилучшего качества связи. Метеорологу — для размещения станций слежения за погодой.
Для некоторых задача решается легко. Например, если , мы можем взять куб и его вершины будут являться ответом к задаче. Также нам повезёт, если будет равно количеству вершин икосаэдра, додекаэдра или другого платонова тела. В противном случае задача не столь проста.
Для достаточно большого количества точек есть формула с эмпирически подобранными коэффициентами, ещё несколько вариантов — здесь, здесь, здесь, и здесь. Но есть и более универсальное, хотя и более сложное решение, которому посвящена данная статья.
Решим задачу, очень похожую на задачу Томсона (wiki). Разбросаем точек случайно, а потом заставим их притягиваться к какой-то поверхности, например к сфере, и отталкиваться друг от друга. Притяжение и отталкивание определяются функцией — потенциалом. При минимальном значении потенциальной функции точки будут лежать на сфере наиболее равномерно.
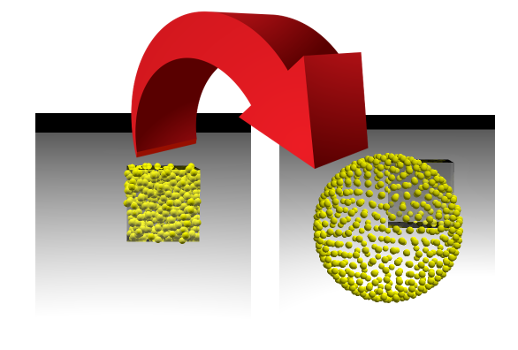
Эта задача очень похожа на процесс обучения моделей machine learning (ML), в ходе которого минимизируется функция потерь. Но дата-сайентист обычно смотрит, как уменьшается одно единственное число, а мы сможем наблюдать за изменением картинки. Если у нас всё получится, то мы увидим, как точки, случайно размещённые внутри куба со стороной 1, разойдутся по поверхности сферы:
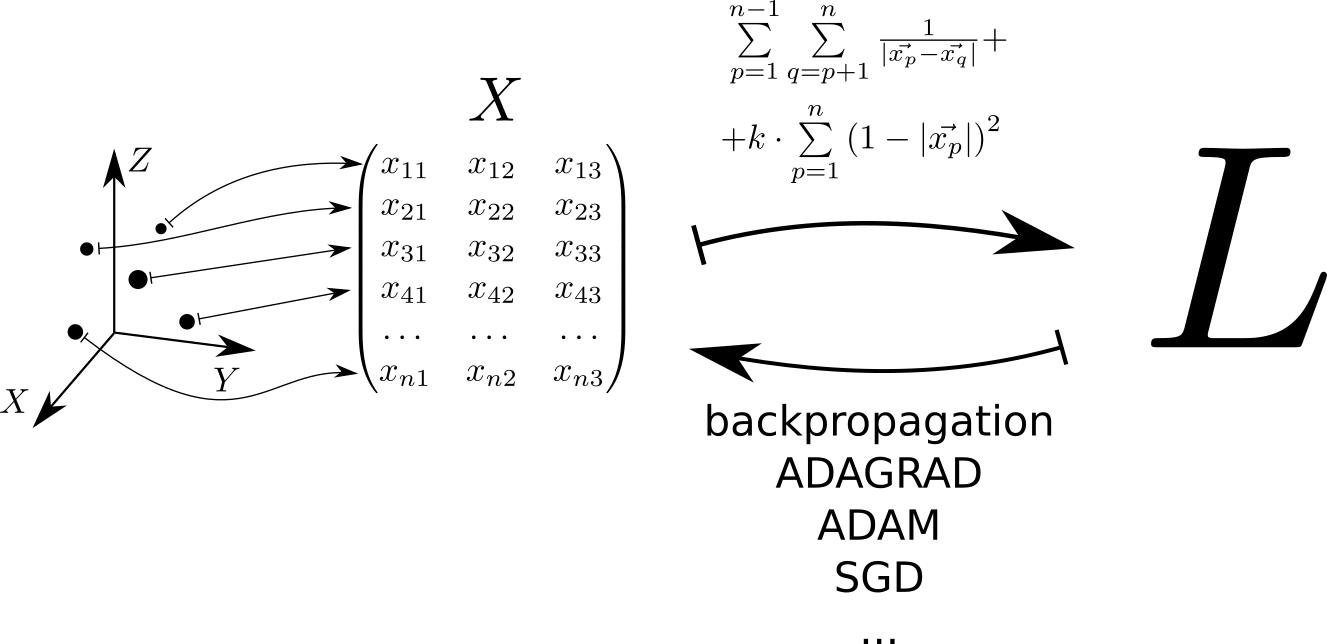
Схематически алгоритм решения задачи можно представить следущим образом. Каждой точке, расположенной в трёхмерном пространстве, соответствует строчка матрицы . По этой матрице рассчитывается функция потерь , минимальному значению которой соответствует равномерное распределение точек по сфере. Минимальное значение находится с помощью библиотек pytorch и tensorflow, позволяющих вычислять градиент функции потерь по матрице и спускаться в минимум, используя один из реализованных в библиотеке методов: SGD, ADAM, ADAGRAD и т.д.
Считаем потенциал
Благодаря своей простоте, выразительности и способности служить интерфейсом к библиотекам, написанным на других языках, Python широко используется для решения задач машинного обучения. Поэтому примеры кода в этой статье написаны на Python. Для проведения быстрых матричных вычислений будем использовать библиотеку numpy. Для минимизации функции многих переменных — pytorch и tensorflow.
Случайно разбрасываем точки в кубе со стороной 1. Пусть у нас будет 500 точек, а упругое взаимодействие в 1000 раз более значимо, чем электростатическое:
import numpy as np
n = 500
k = 1000
X = np.random.rand(n, 3)Этот код сгенерировал матрицу размером , заполненную случайными числами от 0 до 1:
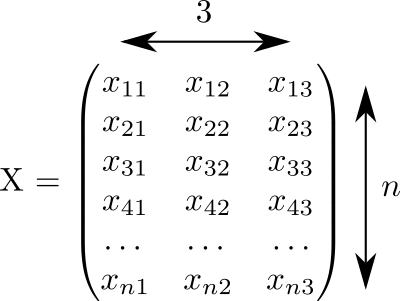
Будем считать, что каждая строка этой матрицы соответствует одной точке. А в трёх столбцах записаны координаты всех наших точек.
Потенциал упругого взаимодействия точки с повехностью единичной сферы . Потенциал электростатического взаимодействия точек и — . Полный потенциал складывается из электростатического взаимодействия всех пар точек и упругого взаимодействия каждой точки с поверхностью сферы:
В принципе, можно посчитать значение потенциала по этой формуле:
L_for = 0
L_for_inv = 0
L_for_sq = 0
for p in range(n):
p_distance = 0
for i in range(3):
p_distance += x[p, i]**2
p_distance = math.sqrt(p_distance)
L_for_sq += k * (1 - p_distance)**2 # квадрат расстояния от поверхности сферы, умноженный на константу упругости
for q in range(p + 1, n):
if q != p:
pq_distance = 0
for i in range(3):
pq_distance += (x[p, i] - x[q, i]) ** 2
pq_distance = math.sqrt(pq_distance)
L_for_inv += 1 / pq_distance # обратное расстояние между двумя точками
L_for = (L_for_inv + L_for_sq) / n
print('loss =', L_for)Но есть небольшая беда. Для жалких 2000 точек эта программа будет работать 2 секунды. Гораздо быстрее будет, если мы посчитаем эту величину, используя векторизованные матричные вычисления. Ускорение достигается как за счёт реализации матричных операций с помощью "быстрых" языков fortran и C, так и за счёт использования векторизированных операций процессора, позволяющих за один такт выполнить действие над большим количеством входных данных.
Посмотрим на матрицу . Она обладает многими интересными свойствами и часто встречается в выкладках, связанных с теорией линейных классификаторов в ML. Так, если считать что в строчке матрицы с индексами и записаны вектора трёхмерного пространства , то матрица будет состоять из скалярных произведений этих векторов. Таких векторов штук, значит размерность матрицы равна .
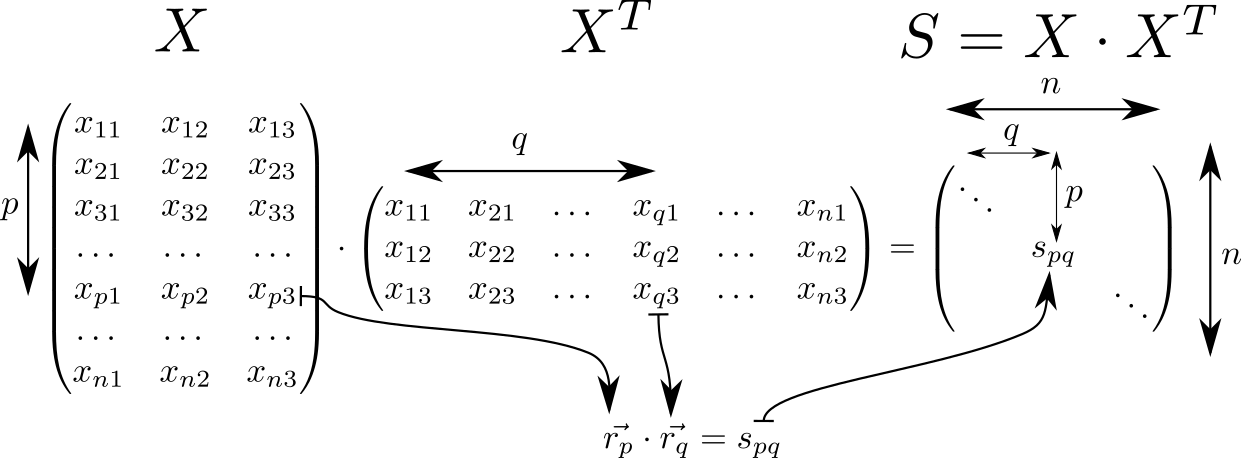
На диагонали матрицы стоят квадраты длин векторов . Зная это, давайте считать полный потенциал взаимодействия. Начнём с расчёта двух вспомогательных матриц. В одной диагональ матрицы будет повторяться в строках, в другой — в столбцах.
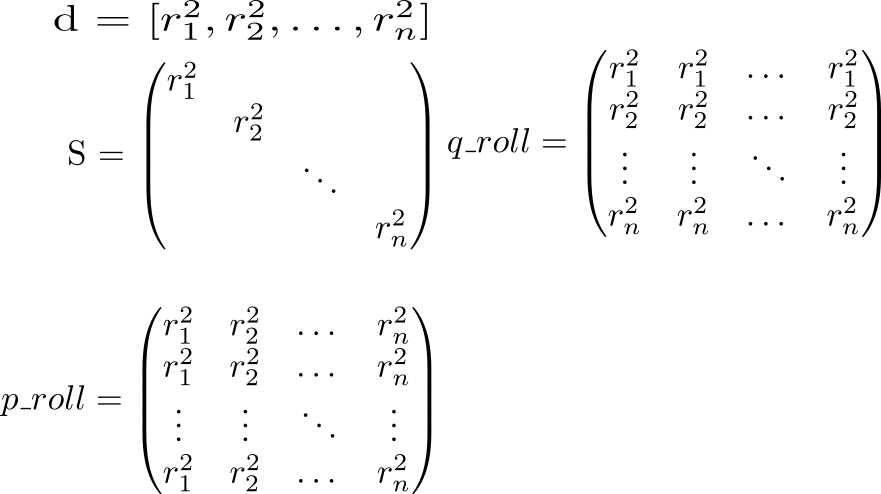
Посмотрим теперь на значение выражения p_roll + q_roll - 2 * S
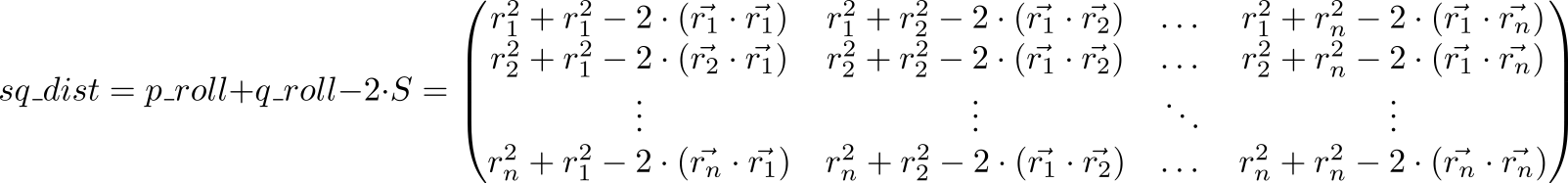
Элемент с индексами матрицы sq_dist равен . То есть, у нас получилась матрица квадратов расстояний между точками.
Электростатическое отталкивание на сфере
dist = np.sqrt(sq_dist) — матрица расстояний между точками. Нам нужно посчитать потенциал, учитывающий отталкивание точек между собой и притяжение к сфере. Поставим на диагональ единицы и заменим каждый элемент на обратный ему (только не подумайте, что мы при этом обратили матрицу!): rec_dist_one = 1 / (dist + np.eye(n)). Получилась матрица, на диагонали которой стоят единицы, другие элементы — потенциалы электростатического взаимодействия между точками.
Добавим теперь квадратичный потенциал притяжения к поверхности единичной сферы. Расстояние от поверхности сферы . Возводим его в квадрат и умножаем на , который задаёт соотношение между ролью электростатического отталкивания частиц и притяжения сферы. Итого k = 1000, all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2. Долгожданная функция потерь, которую мы будем минимизировать: t = all_interactions.sum()
Программа, рассчитывающая потенциал с помощью библиотеки numpy:
S = X.dot(X.T) # матрица скалярных произведений
pp_sq_dist = np.diag(S) # диагональ
p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) # размножаем диагональ по столбцам
q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) # размножаем диагональ по строкам
pq_sq_dist = p_roll + q_roll - 2 * S # квадраты расстояний между парами точек
pq_dist = np.sqrt(pq_sq_dist) # расстояния между точками
pp_dist = np.sqrt(pp_sq_dist) # расстояния до поверхности единичной сферы
surface_dist_sq = (pp_dist - np.ones(n)) ** 2 # квадраты расстояний до поверхности единичной сферы
rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) # потенциалы электростатического отталкивания между точками
L_np_rec = rec_pq_dist.sum() / 2 # полный потенциал электростатического взаимодействия
L_np_surf = k * surface_dist_sq.sum() # полный потенциал притяжения к поверхности сферы
L_np = (L_np_rec + L_np_surf) / n # часть полного потенциала, приходящаяся на одну точку
print('loss =', L_np)Здесь дела обстоят чуть лучше — 200 мс на 2000 точек.
Используем pytorch:
import torch
pt_x = torch.from_numpy(X) # pt_x - объект класса tensor из библиотеки pytorch
pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication
pt_pp_sq_dist = pt_S.diag()
pt_p_roll = pt_pp_sq_dist.repeat(n, 1)
pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n)
pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S
pt_pq_dist = pt_pq_sq_dist.sqrt()
pt_pp_dist = pt_pp_sq_dist.sqrt()
pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2
pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64)
L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n
print('loss =', float(L_pt))И, наконец, tensorflow:
import tensorflow as tf
tf_x = tf.placeholder(name='x', dtype=tf.float64)
tf_S = tf.matmul(tf_x, tf.transpose(tf_x))
tf_pp_sq_dist = tf.diag_part(tf_S)
tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1))
tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n))
tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S
tf_pq_dist = tf.sqrt(tf_pq_sq_dist)
tf_pp_dist = tf.sqrt(tf_pp_sq_dist)
tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2
tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64)
L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n
glob_init = tf.local_variables_initializer() # отложенное действие инициализации переменных
with tf.Session() as tf_s: # внутри этой сессии работаем
glob_init.run() # выполнили инициализацию
res, = tf_s.run([L_tf], feed_dict={tf_x: x}) # всё посчитали
print(res)Сравниваем производительность этих трёх подходов:
| N | python | numpy | pytorch | tensorflow |
| 2000 | 4.03 | 0.083 | 1.11 | 0.205 |
| 10000 | 99 | 2.82 | 2.18 | 7.9 |
Векторизованные вычисления дают выигрыш более чем на полтора десятичных порядка относительно кода на чистом python. Виден "boiler plate" у pytorch: вычисления малого объёма занимают заметное время, но оно почти не изменяется при увеличении объёма вычислений.
Визуализация
В наше время данные можно визуализировать средствами огромного количества пакетов, таких как Matlab, Wolfram Mathematics, Maple, Matplolib и т. д. и т. п. В этих пакетах очень много сложных функций, делающих сложные вещи. К сожалению, если перед тобой стоит простая, но нестандартная задача, ты оказываешься безоружен. Моё любимое решение в такой ситуации — povray. Это очень мощная программа, которую обычно применяют для создания фотореалистичных изображений, но её можно использовать как "ассемблер визуализации". Обычно, сколь бы сложной ни была поверхность, которую хочется отобразить, достаточно попросить povray нарисовать сферы с центрами, лежащими на этой поверхности.
С помощью библиотеки vapory можно создать povray-сцену прямо в python, отрендерить её и посмотреть на результат. Сейчас он выглядит так:

Картинка получена так:
import vapory
from PIL import Image
def create_scene(moment):
angle = 2 * math.pi * moment / 360
r_camera = 7
camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30)
light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1])
light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1])
plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1]))
box = vapory.Box([0, 0, 0], [1, 1, 1],
vapory.Pigment('Col_Glass_Clear'),
vapory.Finish('F_Glass9'),
vapory.Interior('I_Glass1'))
spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x]
return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc'])
for t in range(0, 360):
flnm = 'out/sphere_{:03}.png'.format(t)
scene = create_scene(t)
scene.render(flnm, width=800, height=600, remove_temp=False)
clear_output()
display(Image.open(flnm))Из кучи файлов анимированный gif собирается с помощью ImageMagic:
convert -delay 10 -loop 0 sphere_*.png sphere_all.gifНа github можно увидеть рабочий код, фрагменты которого приведены здесь. Во второй статье я расскажу о том, как запустить минимизацию функционала, чтобы точки вышли из куба и равномерно расползлись по сфере.
Комментарии (6)

Dronablo
25.09.2018 17:49Pythran и numba сходу позволяют получить решение в 20 раз быстрее вашего numpy варианта в пару строк кода, а если покопаться, то, может быть, и быстрее. А еще я бы сюда рассказал про line_profiler, который помогает понимать где именно мы тратим время.

startars Автор
25.09.2018 17:58Большое спасибо за ссылки. К сожалению, расчёт функции потерь не является самоцелью. Основная особенность приведённого в статье кода — возможность использования pytorch и tensorflow для расчёта градиента функции потерь с помощью backpropagation и нахождение расположения точек, минимизирующего функцию потерь. Интересно будет сравнить по производительности Ваш вариант минимизации функции многих переменных с тем, что получится, если использовать методы оптимизации из этих библиотек.


HOMPAIN
Так и не понял зачем вам матрицы, кроме того что вы в ней значения храните?
Зачем вам потенциал взаимодействия с поверхностью сферы, когда по условию точка должна находиться на её поверхности и это условие элементарно реализуется. Вы этим усложняете себе задачу и скорость её решения и также можете получить побочные решения, когда точки будут симметрично отклоняться от поверхности в обе стороны.
startars Автор
HOMPAIN, большое спасибо за комментарий!
Вы всё поняли совершенно правильно. Матрица нужна для того, чтобы хранить в ней координаты точек. Этот подход позволяет эффективно использовать возможности библиотек numpy, pytorch и tensorflow, тем самым обойдя «медленность» языка Python.
Полностью с Вами согласен. Условие нахождения точки на поверхности сферы может быть элементарно реализовано. Например, нормированием векторов на их длину. И это является одним из способов решения задачи получения случайно раскиданных по сфере точек с равномерной плотностью вероятности.
Так же полностью согласен с тем что рассмотрение квадратичного потенциала может уменьшить скорость схождения алгоритма. Более аккуратным будет решение с использованием множителей Лагранжа и линейным по расстоянию штрафом. Будем живы, рассмотрю этот подход ;)
К сожалению не могу согласиться с тем, что точки будут симметрично отклоняться от поверхности в обе стороны. Квадратичный потенциал взаимодействия с поверхностью единичной сферы действительно инвариантен относительно смены знака расстояния до поверхности. Но взаимодействие точек между собой не инвариантно. Помещение точек под поверхность сферы увеличит энергию взаимодействия. Поэтому в ходе уменьшения целевой функции будет выбран вариант где точки летают над поверхностью единичной сферы, как это изображено на картинке, с которой начинается статья.