Предупреждение врача. Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.
Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.
Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).
Наслаждайтесь. И не говорите, что врач не предупреждал.
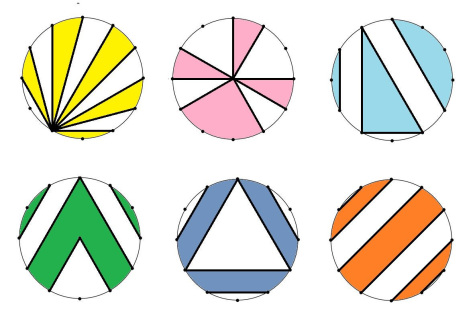
Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)
«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».
(Как по мне, это классика).
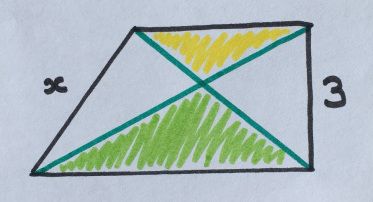
В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?
«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».

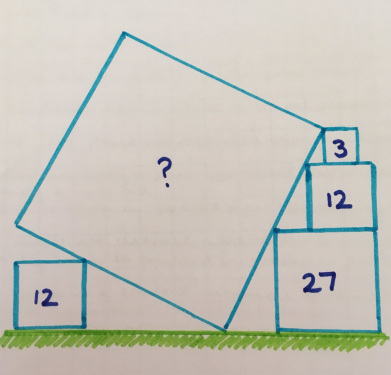
Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?
«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».
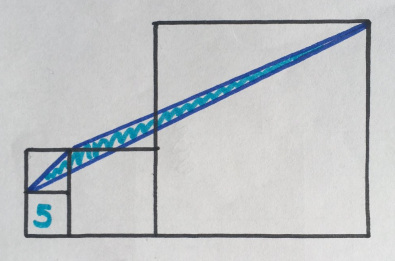
Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?
«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».

«Ещё одна переделка, которую я предпочитаю оригиналу».
«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».

Какова площадь круга?
«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»
У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.
«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»
У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?
«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».

«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».
Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?
«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».
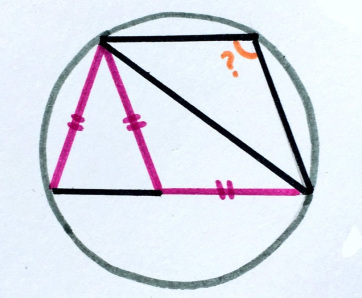
Все четыре треугольника равнобедренные. Найдите угол.
«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»

На картинке больше зелёного цвета или синего (и на сколько)?
«Ещё одна из моих любимых».
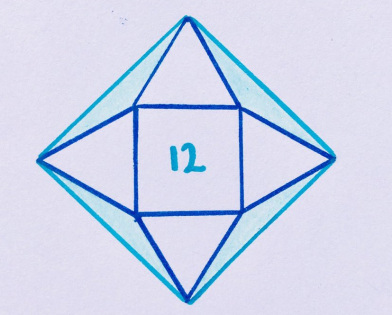
Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?
«Тут самое лучшее — действительно хорошие решения по рассечению площади».
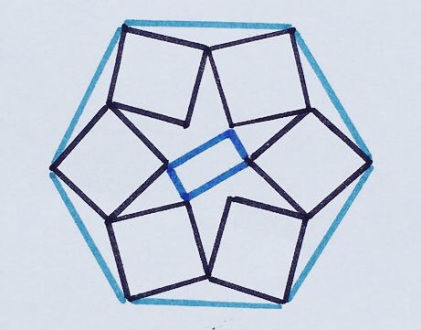
Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?
«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»
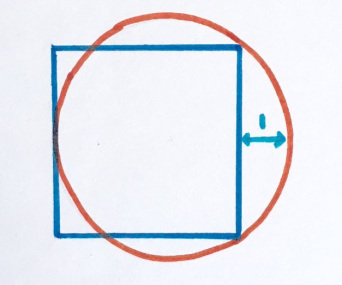
Какова площадь этого квадрата?
«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».

Какая часть большого квадрата закрашена?
«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».
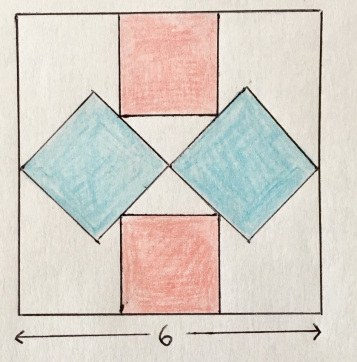
У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?
«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».

Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.
«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».
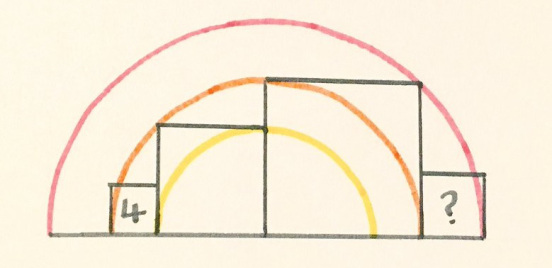
У левого квадрата площадь 4. Какова площадь правого квадрата?
«Мне нравится эта задачка, она напоминает закат над городом скверов.”
Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.
Как вы пришли к разработке своих головоломок?
Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.
Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.
Как проходит творческий процесс?
Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.
Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?
Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.
Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.
Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.
Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?
Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!
Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!
Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.
Советы для потенциальных создателей головоломок?
Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.
Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:
В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы. Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.
Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.
Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).
Наслаждайтесь. И не говорите, что врач не предупреждал.
1. Сад часов

Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)
«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».
2. Опрокинутый квадрат

(Как по мне, это классика).
3. Это ловушка

В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?
«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».
4. Три квадратных тарелки

Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?
«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».
5. Красивая стрижка

Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?
«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».
6. Все люди рождены равными

«Ещё одна переделка, которую я предпочитаю оригиналу».
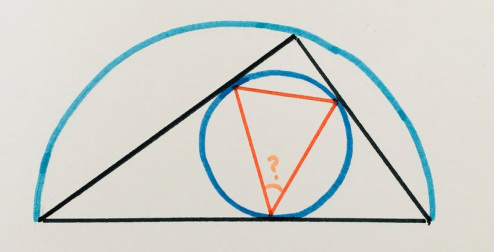
7. Полукруг турдакен

«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».
8. Степенные хорды

Какова площадь круга?
«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»
9. Сказка о двух кругах
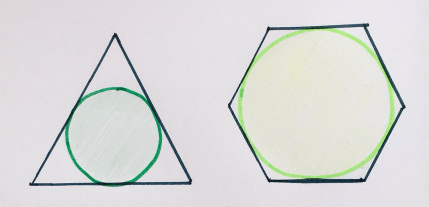
У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.
«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»
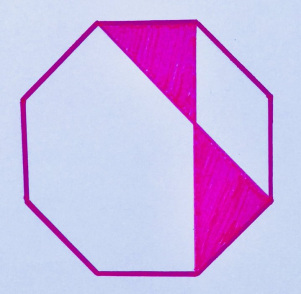
10. Doc Oct

У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?
«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».
11. Всё в квадрате

«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».
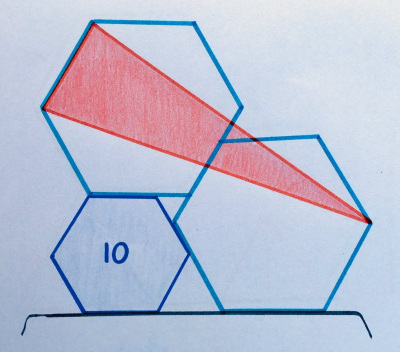
12. Шип в улье

Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?
«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».
13. Я видел равнобедренных

Все четыре треугольника равнобедренные. Найдите угол.
«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»
14. Зеленый против синего

На картинке больше зелёного цвета или синего (и на сколько)?
«Ещё одна из моих любимых».
15. Резцы по камню

Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?
«Тут самое лучшее — действительно хорошие решения по рассечению площади».
16. Едем, едем, уехалиугольник

Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?
«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»
17. Только один факт

Какова площадь этого квадрата?
«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».
18. Стиральная машина

Какая часть большого квадрата закрашена?
«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».
19. Летающие флаги

У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?
«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».
20. Тигрогон

Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.
«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».
БОНУС:
Закат над Квадратным городом
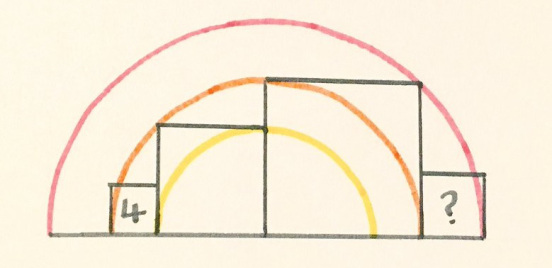
У левого квадрата площадь 4. Какова площадь правого квадрата?
«Мне нравится эта задачка, она напоминает закат над городом скверов.”
Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.
Как вы пришли к разработке своих головоломок?
Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.
Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.
Как проходит творческий процесс?
Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.
Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?
Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.
Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.
Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.
Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?
Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!
Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!
Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.
Советы для потенциальных создателей головоломок?
Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.
Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:
- Красивая постановка задачи. Предоставьте минимум информации, чтобы читателю стало интересно, как вообще можно решить такую задачу. Или несколько дразнящих кусочков информации, каждый из которых якобы предлагает способ решения. Правильные многоугольники и круги — фантастические штуки, потому что скрывают огромное количество информации.
- Красивый метод. Трюк или кратчайший путь, или внезапное озарение, которое всё упрощает. Это может быть не самый очевидный метод. Я видела много задачек, которые решаются с помощью алгебры или иррациональных чисел, или ужасных выражений с pi, а в конце всё внезапно сокращается — и я понимаю, что есть более простой способ.
- Красивый ответ. Мало удовольствия работать над головоломкой, чтобы в конце получить некрасивый ответ.
В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы. Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.


Zangasta
MaxVetrov
А тут в чем головоломка?
Zangasta
Каким образом торговец, у которого на телеге бочка яблочной водки и бочка сидра (по 31 1/2 галлона в каждой бочке), может отлить покупателю на 21 доллар 6 центов напитка «Утренняя роса», который представляет собой не что иное, как смесь водки и сидра. У продавца есть только меры в 2 и 4 галлона, а покупателю нужно полностью наполнить свой бочонок вместимостью 26 галлонов.
MaxVetrov
А доли какие для водки и сидра в напитке?
Zangasta
Это головоломка, сударь. Извольте как-нибудь сами додуматься.
gecube
Задачки реально здоровские. Весело провожу время. Можно было ответы загнать под спойлеры для самопроверки.
geisha
Они здоровские, но несложные если сравнивать с олимпиадными. В большинстве — излишне много симметрий.
gecube
Симметрия — это как правило, красиво. Так что я не против нее ) Пускай, задачки будут красивые, это позволит привлечь к их решению бОльшую аудиторию, а, значит, сделать полезное дело развития человеческого потенциала.
CaptainFlint
В шестой задаче перевод убил важную деталь. Треугольники выглядят равносторонними, но в условии задачи это не указывается. Однако оригинал явно использует слово «equilateral» в заголовке, тогда как в переводе используется «равный», что не является равноценным заменителем.
gecube
Это игра слов. Если что — я понял, что треугольники именно равносторонние…
CaptainFlint
В том-то и дело, что не должно быть игры слов. В оригинале так и звучит: «Все люди рождены (или созданы) равносторонними». То есть намеренная замена слова «равный» из расхожей фразы на совершенно неуместное слово «равносторонний», специально, чтобы уточнить задачу. А в переводе эту замену почему-то не воспроизвели, и часть условия исчезла. Конечно, догадаться можно, да и вид самих треугольников на картинке намекает. Но всё-таки в геометрии полагается не намекать, а говорить более прямо. (Конечно, «рождены равносторонними» — тоже не самый прямой способ выражения условий задачи, но всё же абсурдность фразы является явным указанием, что слово тут используется не просто так, а в переводе даже этой абсурдности нету.)
gecube
Согласен, что термин «равные» относится не к сторонам, а к площадям. Возможно, было бы удачнее, если были внесены изменения в картинку, которые явно показали, что стороны равные (хотя переводчик на это права, конечно, не имеет).
MUTbKA98
Задача #5 вообще странная — размер самого большого квадрата выглядит абсолютно произвольным. Или в ответе предполагается зависимость площади треугольника от параметров этого квадрата?
Zangasta
Нет.
Совершенно не интуитивный ответ, правда?
apachik
вас подвел перевод. Но если загуглить, то находим ответ.
mathworld.wolfram.com/Shear.html
Метод на самом деле называется не «стрижка», а сдвиг. Ну вот и начинайте играться с размером большого квадрата :)
Tyusha
Задачи замечательны тем, что кажется недостаёт данных. Но это наводит на мысль, что от них ничего и не зависит. Поэтому брала удобный частный случай, например в задаче #5 можно стянуть большой квадрат в точку, а в задаче #7 рассмотреть строго симметричный вариант.
Однако получив простой ответ, сложно доказать, что в остальных случаях результат будет таким же.
MUTbKA98
Вот поэтому я все же за более строгие формулировки условий — потому как кажется, что «а вдруг ты что-то просмотрел?» — ну там, к примеру — «вот это пересечение посреди отрезка, или это случайность»? В итоге может решаться несколько не та задача, о которой думал автор. :)
CaptainFlint
Середина отрезка — всё-таки, скорее всего, нет (если явно не отмечено или не следует из других условий).
zartarn
Мне нравится вот эта задачка со звездочкой, учебника 6-8 класса
m03r
zartarn
Пусть сторона квадрата = а.
Находим площадь сектора = площадь круга / 4= pi*r*r/4, r = a => pi*a*a/4
Площадь треугольника с основание a и высотой a = (1/2)*a*a
Закрашненая площадь = (площадь сектора — площадь треугольника)*2 = 2*((Pi*a^2)/4 — (a^2)/2) = (pi*a^2)/2 — a^2 = (pi/2 -1)*a^2
m03r
Так я вроде точную площадь и нахожу. Только не расписал, потому что уже неинтересно.
zartarn
А в 8 классе разве проходят площадь сектора через угол? я честно не помню:) Вроде бы в 6-8 классе этого еще небыло. Если было, то да, всё проще. У меня без этого найти не получилось. Но мне после вышки как то сложно стало переключаться с интегралов и матриц)).
gecube
А мне проще простыми методами — типа отношения площадей секторов и т.д. По крайней мере, это на пальцах проще объяснить.
m03r
Площадь сектора через угол, кажется, настолько очевидно, что это можно и не проходя сообразить…
zartarn
Только это мы смотрим с багажем своего опыта.
Я тут полистал учебники, в 8 классе синус/косинус проходят как отношения катетов и гипотенузы, потом в 9 классе — как функции угла в градусах, наконец в 10 классе — как функции радиан и чисел со всеми формулами.
Так что в 8 классе возможно и решили бы через площадь сектора.
Alek_roebuck
Третья устная, пятая устная, остальные не смотрел. Надо сделать поправку: в России зачем-то по традиции продолжают учить геометрии весьма серьезно. Не знаю, откуда автор этих задач, но в США такой материал показался бы очень сложным, в России же, как мне кажется, его спокойно можно давать в 8 классе в качестве обычных упражнений.
SilverHorse
Три человека, периодически поправлявшие друг друга, давным-давно выпустившиеся из школы и местами подзабывшие школьный курс геометрии, независимо друг от друга решили большую часть за 3 с копейками часа, частично в уме.
Для российских реалий на технарском ресурсе ремарка о 6 месяцах в конце выглядит немного неуместно)
3dcryx
Что-то я не могу понять 7 задачу. Что там дано и что нужно найти?
CaptainFlint
В полукруг вписан треугольник, в него — круг, в него — треугольник с вершинами в точках касания. Найти угол, отмеченный вопросом.
Sirion
Эдакий современный аналог сангаку. Но очень примитивно. За полчаса я решил штук пять методом пристального взгляда, без чертежей и записей. Потом надоело.
vesper-bot
Странно. В задаче №3 верхняя сторона трапеции равна боковой, или нет? А то решений получается бесконечное число.
2. 135. Угол, на который повернут квадрат, определяется тем, что дальние стороны квадратов 27 и 12 находятся на одной прямой.
4. 75 (неперекрывающаяся). Т.е. квадраты со сторонами 4, 5, 6 и перекрытие 2х1.
6. 15. Хинт: центральный треугольник получается равносторонним.
7. 45 градусов (могу ошибиться здесь). Вариант решения: предположить основной треугольник равнобедренным.
13. 108 градусов. 4-й треугольник составной, у которого равные стороны нижняя и диагональ ромба в середине. Дальше считаем уравнение на равенство углов у левого нижнего треугольника, выразив их через искомый двумя путями.
15. 12. Вообще говоря, равна площади квадрата. Если сторона квадрата Х, то площадь одного закрашенного треугольника равна Х*Х*sin(150grad)/2 = X^2/4.
18. 40%. Если принять сторону квадрата за 1, то на рисунке появляется прямоугольник 1х3, вписанный в круг диаметром равный стороне описанного квадрата. Диаметр sqrt(10), площадь квадрата 10, а квадратов внутри 4.
Остальное не пытался решать — забыл уже геометрию.
CaptainFlint
Нет, равенство не требуется.
2. Обозначим верхнее и нижнее основания трапеции как a и b. Площади треугольников Б1+З и Б2+Ж: 1/2 * 3 * b, 1/2 * 3 * a. Вычтем: 1/2 * 3 * (b — a) = З — Ж = 6, итого b — a = 4. Заметим, что точные значения a и b нам не нужны.
3. x^2 = 3^2 + (b — a)^2.
vesper-bot
10. 64. Ели сторона восьмиугольника равна 1, то площадь закрашенной фигуры тоже 1, т.е. 1/8 периметра. Так как с увеличением фигуры площадь растет квадратично, а периметр — линейно, нужно увеличить единичный восьмиугольник в 8 раз, чтобы площадь закрашенной части стала равна периметру.
11. 4*пи. Но пришлось загуглить формулы радиуса вписанного круга.
12. 15. Искомая площадь вдвое превышает площадь треугольника с вершиной на противоположной грани этого же шестиугольника, которая в свою очередь втрое меньше площади самого шестиугольника. Размеры большого и маленького шетиугольников различаются в полтора раза, т.е. площадь большого = 22.5.
«Закат» (кстати, в оригинале «sunrise», т.е. рассвет) — 8. Опять через подобие, коэффициент которого — корень из двух.
SilverHorse
4. Неправильно. 5,6,7, площадь 108. 4*sqrt(10) — это гипотенуза прямоугольного треугольника с катетами 12 и 4.
7. Да, 45. Вписанный угол, опирающийся на хорду, является противолежащим к углу, образованным касательными в концах этой хорды, и он всегда вдвое меньше его (а он, в свою очередь, равен 90 как вписанный угол, опирающийся на диаметр).
15. Можно обойтись без синусов, тупо посчитав площади фигур. Площадь большого квадрата 24+12*sqrt(3), площадь фигуры 12+4*3*sqrt(3).
vesper-bot
Про 7 — только потом вспомнил, что есть теорема, что угол на круге равен половине меры дуги, а мера дуги между точками касания круга углом равна 180 градусов минус угол.
Про 15 — ну это как решать удобнее. Мне через синусы.
Про 4 — обидно, но вначале я вообще насчитал 3-4-5 :(
m03r
Tortortor
перевод откровенно хромает
MaxVetrov
Задачка «Закат над Квадратным городом»
Используем теорему Пифагора.
Ответ: 8
Общий ответ не проверял, но судя по этому частному ответу — площадь удваивается. И это можно использовать для геометрического удвоения площади квадрата.
CaptainFlint
Прячьте ответы и решения под спойлеры, пожалуйста.
finlandcoder
Я лучше про сортировочки на собеседовании расскажу, чем такое решать.
MaxVetrov
Не совсем удачно правый синий квадрат получился, ну и ладно.
GeMir
Ещё на brilliant.org неплохие задачки для любителей подумать дольше пары минут над решением попадаются.
cyberzx23
Такое ощущение, что у неё все задачи любимые
catanfa
Кто полностью забыл теоремы, и помнит только теорему Пифагора, может решить задачу 17, где круг вписан в квадрат.
при этом BD = x/2 из равенства треугольников BCD и CDE по двум сторонам (BC и CE радиусы, СD — общая) и прямому углу