Главная
Принцип наименьшего действия в аналитической механике

Принцип наименьшего действия в аналитической механике +29

10.10.2018 15:35

maisvendoo 65 4900 Источник

Предыстория

Причина данной публикации — неоднозначная статья на тему принципа наименьшего действия (ПНД), опубликованная на ресурсе несколько дней назад. Неоднозначна она потому, что её автор в популярной форме пытается донести до читателя один из основополагающих принципов математического описания природы, и это частично ему удается. Если бы не одно но, притаившееся в конце публикации. Под спойлером приведена полная цитата данного отрывка

Задача о движении шарика

Не все так просто

На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.

Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.

Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.

Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.

Так в чем же, с моей точки зрения, проблема?

Проблема в том, что автор, приводя данный пример допустил ряд фундаментальных ошибок. Она усугубляется тем, что планируемая вторая часть, со слов автора, будет опираться на эти ошибки. Руководствуясь принципом наполнения ресурса достоверной информацией я вынужден выступить с разъяснением своей позиции по данному вопросу более развернуто, и формат комментариев для этого маловат.

Данная статья расскажет о том, как строится механика на базе ПНД, и постарается объяснить читателю, что проблема, которую ставит автор цитируемой публикации отсутствует.

1. Определение действия по Гамильтону. Принцип наименьшего действия

Действием по Гамильтону называют функционал

$S = \int\limits_{t_1}^{t_2} \, L\left(\mathbf q(t), \dot{\mathbf q}(t) \right) \, dt$

где

$L\left(\mathbf q(t), \dot{\mathbf q}(t) \right) = T\left(\mathbf q(t), \dot{\mathbf q}(t) \right) - \Pi(\mathbf q)$

— функция Лагранжа, для некоторой механической системы, в которой (опуская аргументы в дальнейшем) T — кинетическая энергия системы; П — потенциальная её энергия; q(t) — вектор обобщенных координат этой системы, являющийся функцией времени. при этом полагают, что моменты времени t₁ и t₂ — фиксированы.

Почему функционал, а не функция? Потому, что функция, по определению есть правило, по которому одному числу из области определения (аргументу функции) ставится в соответствие другое число из области значений. Функционал отличается тем, что качестве его аргумента выступает не число, а целая функция. В данном случае это закон движения механической системы q(t), определенный по крайней мере на промежутке времени между t₁ и t₂.

Многолетние (и это мягко сказано!) труды ученых-механиков (включая умопомрачительного Леонарда Эйлера), позволили сформулировать

Принцип наименьшего действия:

Механическая система, для которой задана функция Лагранжа $L\left(\mathbf q(t), \dot{\mathbf q}(t) \right)$ , движется таким образом, что закон её движения q(t) доставляет минимум функционалу

$S = \int\limits_{t_1}^{t_2} \, L\left(\mathbf q(t), \dot{\mathbf q}(t) \right) \, dt \to \min$

называемому действием по Гамильтону.

Уже из самого определения ПНД следует тот факт, что данный принцип приводит к уравнениям движения лишь для ограниченного класса механических систем. Для каких? А давайте разберемся.

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

Как следует из определения, опять таки, функции Лагранжа, ПНД позволяет получить уравнения движения для механических систем, силовое воздействие на которые определяется исключительно потенциальной энергией. Для того чтобы разобраться, о каких системах идет речь, дадим несколько определений, которые, для экономии объема статьи я помещаю под спойлер

Работа силы на перемещении

Рассмотрим движущуюся по траектории AB точку, к которой приложена сила

$\vec F$ . Бесконечно малое перемещение точки по траектории определяется вектором

$d\vec s$ , направленным по касательной к траектории.

Элементарной работой силы

$\vec F$ на перемещении

$d\vec s$ называют скалярную величину, равную

$dA = \vec F \cdot d\vec s$

Тогда, полная работа силы на перемещении точки по траектории AB есть криволинейный интеграл

$A = \int\limits_{AB} \, \vec F \cdot d\vec s$

Кинетическая энергия точки

Кинетической энергией точки T называют работу, которую должны совершить приложенные к точке массой m силы, для того чтобы из состояния покоя перевести точку в движение со скоростью $\vec v$

Вычислим кинетическую энергию, согласно данному определению. Пусть точка начинает движение из состояния покоя под действием приложенных к ней сил. На отрезке траектории AB она приобретает скорость

$\vec v$ . Вычислим работу, совершенную приложенными к точке силами, которые, по принципу независимости действия сил, заменим равнодействующей

$\vec F$

$T = A = \int\limits_{AB} \, \vec F \cdot d\vec s$

В соответствии со вторым законом Ньютона

$\vec F = m \, \vec a = m \, \frac{d\vec v}{dt}$

тогда

$T = \int\limits_{AB} \, \vec F \cdot d\vec s = m \, \int\limits_{AB} \frac{d\vec v}{dt} \, \cdot d\vec s = m \int\limits_{AB} \, \vec v \cdot d\vec v$

Вычислим строго стоящее под знаком интеграла скалярное произведение, для чего продифференцируем по времени скалярное произведение вектора скорости самого на себя

$\frac{d}{dt}(\vec v \cdot \vec v) = \frac{d\vec v}{dt} \cdot \vec v + \vec v \cdot \frac{d\vec v}{dt} = 2 \, \vec v \cdot \frac{d\vec v}{dt} \quad (1)$

С другой стороны,

$\vec v \cdot \vec v = v^2$

Дифференцируя это равенство по времени, имеем

$\frac{d}{dt}(\vec v \cdot \vec v) = \frac{d}{dt}(v^2) = 2 \, v \, \frac{dv}{dt} \quad(2)$

Сравнивая (1) и (2) приходим к выводу, что

$\vec v \cdot d\vec v = v \, dv$

Тогда, спокойно вычисляем работу, раскрывая криволинейный интеграл через определенный, взяв в качестве пределов модуль скорости точки в начале и в конце траектории

$T = m \int\limits_{AB} \vec v \cdot d\vec v = m \int\limits_0^v v \, dv = \frac{m\,v^2}{2}$

Консервативные силы и потенциальная энергия точки

Рассмотрим действующую на точку силу, причем такую, что величина и направление этой силы зависит исключительно от положения точки в пространстве

$\vec F = \vec F(x, y, z)\quad(3)$

Пусть точка перемещается в пространстве по произвольной траектории AB. Вычислим, какую работу при этом совершит сила (3)

$A = \int\limits_{AB} \vec F \cdot d\vec s = \int\limits_{AB} \left(F_x \, dx + F_y \, dy + F_z \, dz\right)$

Так как проекции силы на оси координат зависят исключительно от этих самых координат, всегда можно найти функцию

$display$

такую, что

$F_x = \frac{\partial U}{\partial x},\quad F_y = \frac{\partial U}{\partial y},\quad F_z = \frac{\partial U}{\partial z}$

Тогда, выражение для работы преобразуется к виду

$A = \int\limits_{AB} \left(\frac{\partial U}{\partial x} \, dx + \frac{\partial U}{\partial y} \, dy + \frac{\partial U}{\partial z} \, dz\right) = \int\limits_{U_A}^{U_B} \, dU=U_B - U_A$

где

$U_A,\, U_B$ — значения функции U(x, y, z) в точках A и B соответственно. Таким образом работа рассматриваемой нами силы не зависит от траектории точки, а определяется только значениями функции U в начале и в конце траектории. Такая сила называется консервативной силой, а соответствующая ей функция U(x, y, z) — силовой функцией. Очевидно, что

$\vec F = \nabla\, U$ , а так же равенство нулю работы консервативной силы при движении по замкнутой траектории. Говорят так же, что функция U(x, y, z) задает в пространстве силовое поле.

Потенциальной энергией $\Pi = \Pi(x, y, z)$ точки, в пространстве с заданным силовым полем, называют работу внешних сил, приложенных к ней, которую они совершают при перемещении точки в заданное координатами (x, y, z) положение в пространстве из некоторого произвольного положения, выбранного в качестве начала отсчета уровня потенциальной энергии.

Выберем на рассмотренной ранее траектории точки произвольную точку O, лежащую между точками A и B. Положим, что в точке О потенциальная энергия равна нулю. Тогда, согласно определению

$\Pi_A = -(U_A - U_O)$

— потенциальная энергия точки в положении A, а

$\Pi_B = -(U_B - U_O)$

— потенциальная энергия точки в положении B. Учитывая всё вышесказанное снова вычислим работу потенциальных сил на перемещении из точки A в точку B

$A_{AB} = A_{AO} + A_{OB} = U_O - U_A + U_B - U_O = (U_O - U_A) - (U_O - U_B) = \Pi_A - \Pi_B$

Таким образом, работа консервативных сил равна изменению потенциальной энергии точки, взятому с обратным знаком

$A_{AB} = \Pi_A - \Pi_B = -(\Pi_B - \Pi_A) = -\Delta \Pi$

причем выбор уровня, на котором мы считаем потенциальную энергию равной нулю совершенно не влияет на результат. Отсюда можно сделать вывод, что уровень отсчета потенциальной энергии можно выбрать совершенно произвольно.

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

Итак, рассмотрим теперь механическую систему, движущуюся под действием потенциальных сил, положение которой однозначно задается вектором обобщенных координат

$\mathbf q = \left[q_1, \, q_2, \, \dots,\, q_s \right]^T\quad(4)$

где s — число степеней свободы данной системы.

Действительный, но неизвестный пока нам, закон движения данной системы определяется зависимость обобщенных координат (4) от времени. Рассмотрим одну из обобщенных координат

$inline$ , полагая аналогичные рассуждения и для всех остальных координат.

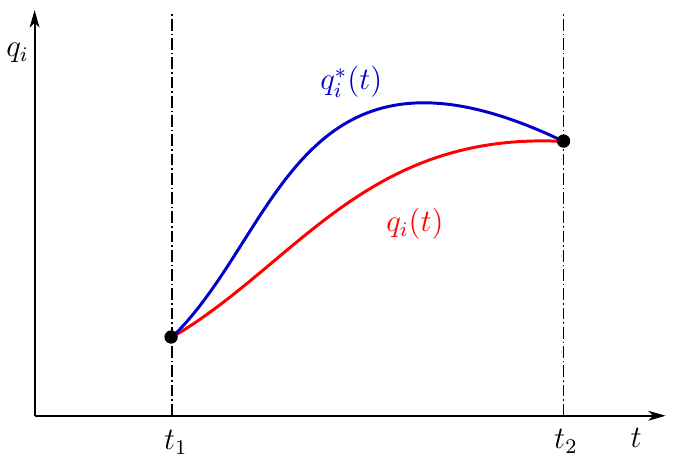
Рисунок 1. Действительное и окольное движение механической системы

На рисунке зависимость

$inline$ изображена красной кривой. Выберем два произвольных фиксированных момента времени t₁ и t₂, полагая t₂ > t₁. Положение системы

$\mathbf q_1 = \mathbf q(t_1)$ договоримся называть начальным положением системы, а

$\mathbf q_2 = \mathbf q(t_2)$ — конечным положением системы.

Однако, я ещё раз настаиваю на том, чтобы нижеследующий текст был прочтен внимательно! Несмотря на то, что мы задаемся начальным и конечным положением системы, ни первое положение, ни второе, нам заранее неизвестны! Равно как и неизвестен закон движения системы! Эти положения рассматриваются именно как начальное и конечное положение, безотносительно конкретных значений.

Далее мы полагаем, что из начального положения в конечное система может придти разными путями, то есть зависимость

$\mathbf q = \mathbf q(t)$ может быть любой кинематически возможной. Действительное движение системы будет существовать в единственном варианте (красная кривая), остальные кинематически возможные варианты будем называть окольными движениями

$\mathbf q^{*} = \mathbf q^{*}(t)$ (синяя кривая на рисунке). Разность между действительным и окольным движением

$\delta q_i(t) = q^{*}_i(t) - q_i(t),\quad \forall i=\overline{1,s}\quad (5)$

будем называть изохронными вариациями обобщенных координат

В данном контексте вариации (5) следует понимать как бесконечно малые функции, выражающие отклонение окольного движения от действительного. Малая «дельта» для обозначения выбрана не случайно и подчеркивает принципиальное отличие вариации от дифференциала функции. Дифференциал — главная линейная часть приращения функции, вызванного приращением аргумента. В случае с вариацией изменение значения функции при постоянном значении аргумента вызвано изменением вида самой функции! Мы не варьируем аргумент, в роли которого выступает время, поэтому вариация называется изохронной. Мы варьируем правило по которому каждому значению времени приводится в соответствие некоторое значение обобщенных координат!

По сути, мы варьируем закон движения, по которому система из начального состояния перемещается в конечное состояние. Начальное и конечное состояние определяются действительным законом движения, но я ещё раз подчеркиваю — их конкретные значения нам не известны и могут быть любыми кинематически возможными, мы лишь полагаем, что они существуют и система гарантированно перемещается из одного положения в другое! В начальном и конечном положении системы мы не варьируем закон движения, поэтому вариации обобщенных координат в начальном и конечном положении равны нулю

$\delta q_i(t_1) = \delta q_i(t_2) = 0,\quad \forall i=\overline{1,s}\quad(6)$

Исходя из принципа наименьшего действия, действительное движение системы должно быть таким, чтобы доставлять минимум функционалу действия. Варьирование координат вызывает изменение функционала действия. Необходимым условием достижения функционалом действия экстремального значения является равенство нулю его вариации

$\delta S = \delta \int\limits_{t_1}^{t2} \, L(q_1,\dots,q_s,\,\dot q_1,\dots,\dot q_s)\,dt = 0\quad(7)$

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

Решим поставленную нами вариационную задачу, для чего вычислим полную вариацию функционала действия и приравняем её к нулю

$\begin{align} \delta S = & \int\limits_{t_1}^{t2} \, L(q_1 + \delta q_1,\dots,q_s + \delta q_s,\,\dot q_1 + \delta\dot q_1,\dots,\dot q_s + \delta\dot q_s)\,dt - \\ &- \int\limits_{t_1}^{t2} \, L(q_1,\dots,q_s,\,\dot q_1,\dots,\dot q_s)\,dt = 0 \end{align}$

Загоним всё под один интеграл, и так как для вариаций справедливы все операции над бесконечно малыми величинами, преобразуем этот крокодил к виду

$\int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \frac{\partial L}{\partial q_i}\delta q_i + \sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}\delta \dot q_i \right]\,dt = 0\quad(8)$

Исходя из определения обобщенной скорости

$\delta \dot q_i = \frac{d(\delta q_i)}{dt}$

Тогда выражение (8) преобразуется к виду

$\int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \frac{\partial L}{\partial q_i}\delta q_i \, dt + \sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}d(\delta q_i) \right] = 0$

Второе слагаемое интегрируется по частям

$\sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}\delta q_i|_{t_1}^{t_2} + \int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \frac{\partial L}{\partial q_i}\delta q_i - \sum\limits_{i=1}^s \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right)\delta q_i \right]\,dt = 0\quad(10)$

Исходя из условия (7), имеем

$\sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}\delta q_i|_{t_1}^{t_2} = 0$

тогда, получаем уравнение

$\int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \left( \frac{\partial L}{\partial q_i} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) \right) \, \delta q_i \right]\,dt = 0$

При произвольных пределах интегрирования равенство нулю определенного интеграла обеспечивается равенством нулю подынтегральной функции

$\sum\limits_{i=1}^s \left[ \frac{\partial L}{\partial q_i} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) \right] \, \delta q_i = 0\quad(11)$

С учетом того, что вариации обобщенных координат независимы, (11) справедливо только в случае равенства нулю всех коэффициентов при вариациях, то есть

$\frac{\partial L}{\partial q_i} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) =0, \quad \forall i = \overline{1,s}$

Никто не мешает нам умножить каждое из уравнений на (-1) и получить более привычную запись

$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) - \frac{\partial L}{\partial q_i} =0, \quad \forall i = \overline{1,s}\quad(12)$

Уравнения (12) и есть решение задачи. И вот на этом моменте ещё раз внимание — решение вариационной задачи по принципу наименьшего действия, это не функция, доставляющая минимум действию по Гамильтону, а система дифференциальных уравнений, решая которое таковую функцию можно найти. В данном случае это дифференциальное уравнение Лагранжа 2-го рода, записанное через функцию Лагранжа, то есть в формулировке для консервативных механических систем.

И всё, на этом принцип наименьшего действия заканчивается, а начинается теория обыкновенных дифференциальных уравнений, которая, в частности, гласит, что решением уравнения (12) является вектор-функция вида

$\mathbf q = \mathbf q(t, C_1, C_2,\dots,C_{2s})$

где C₁,...,C_2s — произвольные константы интегрирования.

Таким образом

ПНД — фундаментальный принцип, позволяющий получить уравнения движения системы, для которой определена функция Лагранжа

Точка! В задачах аналитической механики вышеперечисленные выкладки больше не нужно проделывать, достаточно использовать их результат (12). Функция, удовлетворяющая уравнению (12) есть закон движения системы, удовлетворяющей ПНД.

5. Задача с шариком и стенкой

Теперь вернемся к той задаче, с которой всё началось — об одномерном движении шарика около абсолютно упругой стенки. Разумеется, для данной задачи можно получить дифференциальные уравнения движения. Так как это дифференциальные уравнения движения, то любое, я подчеркиваю это, любое их решение доставляет минимум функционалу действия, а значит ПНД выполняется! Общее решение уравнений движения шарика можно изобразить в виде так называемого фазового портрета рассматриваемой механической системы. Вот этот фазовый портрет

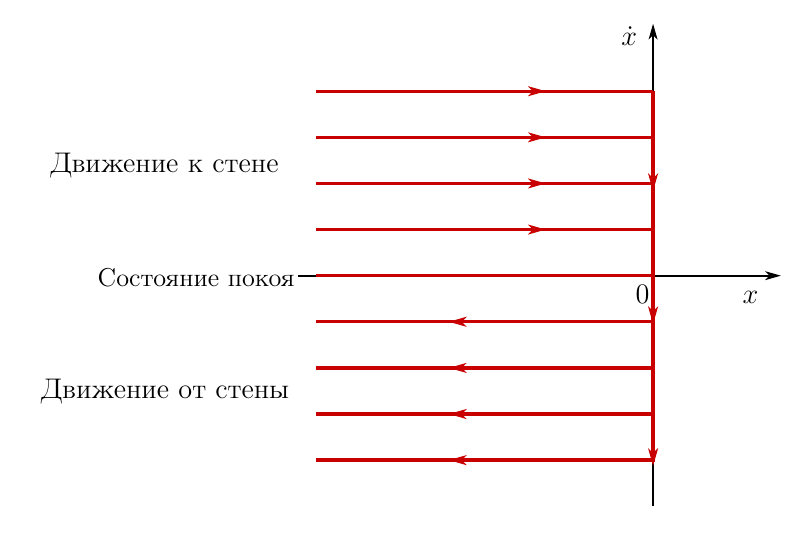
Рисунок 2. Фазовый портрет системы в задаче с шариком

По горизонтальной оси откладывается координата шарика, по вертикальной — проекция скорости на ось x. Может это покажется странным, но данный чертеж отражает все возможные фазовые траектории движения шарика, при любых начальных, или если вам так хочется, краевых условиях. На самом деле параллельных прямых на графике бесконечно много, на чертеже показаны некоторые из них и направление движения по фазовой траектории.

Это — общее решение уравнения движения шарика. Каждая из этих фазовых траекторий доставляет минимум функционалу действия, что непосредственно следует из выкладок, проделанных выше.

Что делает автор задачи? Он говорит: вот шарик покоится, и за промежуток времени от t_A до t_B действие равно нулю. Если шарик толкнуть к стенке, то за тот же промежуток времени действие будет больше, так как у шарика отличная от нуля и неизменная кинетическая энергия. Но почему шарик движется к стенке, ведь в покое действие будет меньше? Значит ПНД испытвает проблемы и не работает! Но мы обязательно решим это в следующей статье.

То что говорит автор — бред. Почему? Да потому, что он сравнивает действия на различных ветвях одной и той же действительной фазовой траектории! Между тем, при применении ПНД, сравнивается действие на действительной траектории и на множестве окольных траекторий. То есть происходит сравнение действия на реальной траектории с действием на тех траекториях, которых нет в природе, и никогда не будет!

Не понятно? Объясню ещё более доходчиво. Рассмотрим состояние покоя. Оно описывается ветвью фазового портрета, совпадающего с осью абсцисс. Координата не меняется с течением времени. Это действительное движение. А какое же движение будет окольным. Любое другое кинематически возможное. Например малые колебания шарика около рассматриваемого нами положения покоя. Задача допускает колебания шарика вдоль оси х? Допускает, значит такое движение кинематически возможно и может рассматриваться как одно их окольных

Почему же шарик таки покоится? Да потому, что действие в состоянии покоя, вычисленное на фиксированном промежутке времени от t_A до t_B, будет меньше действия, при малых колебаниях на том же промежутке времени. Значит колебаниям и любому другому «шевелению» шарика природа предпочитает покой. В полном соответствии с ПНД.

Допустим мы толкнули шарик в сторону стенки. Пусть мы толкнули его как хочет автор, со скоростью, подобранной из краевых условий, так чтобы в момент времени t_B шарик оказался в том же положении, откуда стартовал. Шарик, с постоянной скоростью долетит до стенки, упруго отскочит и вернется в начальное положение в момент времени t_B, опять таки с постоянной скоростью. Ок, это действительное движение. Какое движение будет одним из окольных? Например, если шарик будет двигаться к стенке и от стенки со скоростью, меняющейся со временем. Такое движение возможно кинематически? Возможно. Почему же модуль скорости шарика не меняется? Да потому, что действие на такой фазовой траектории будет иметь минимальное значение, в сравнении с любом другим вариантом, где скорость зависит от времени.

Вот и всё. Ничего такого волшебного тут не происходит. ПНД работает безо всяких проблем.

Выводы и пожелания

ПНД — фундаментальный закон природы. Из него, в частности, вытекают законы механики, например дифференциальные уравнения движения (12). ПНД говорит нам о том, что природа устроена так, что уравнение движения консервативной механической системы выглядит именно как выражение (12) и никак иначе. Большего от него и не требуется.

Не нужно придумывать проблем там где их нет.

Комментарии (65)

KonkovVladimir
10.10.2018 18:58
#19216611
+1
Отличное объяснение все просто и понятно, жаль что в школе не проходят принцип наименьшего действия, видимо проблемы с вычислением минимума функционала.
1. ianzag
  10.10.2018 20:41
  #19217191
  Оно конечно да, но для школы выкладки, приводящие к
  
  > ПНД говорит нам о том, что природа устроена так, что уравнение движения консервативной механической системы выглядит именно как выражение (12) и никак иначе.
  
  … несколько крутоваты.
  1. KonkovVladimir
    11.10.2018 07:56
    #19218723
    При соответствующем обобщении понятий принцип наименьшего действия находит приложения в механике непрерывной среды, в электродинамике, квантовой механике, ОТО и др.
    Это настолько универсальная концепция, что достойна включения в школьную программу.
    В школе нужно учить детей концептуально мыслить, а не зазубривать учебник.
    
    aleksandros
    11.10.2018 13:14
    #19220587
    Снова нападки на школу… Детей и учат мыслить, а также применять полученные знания для решения задач. Но они не хотят размышлять и не хотят думать. Поймите уже. Они в принципе не понимают зачем им «это нужно в жизни». У каждого второго мечта это иметь свой видеоблог и получать за это деньги, всё.
    
    KonkovVladimir
    11.10.2018 13:59
    #19220959
    Дети берут пример со своих родителей, если родители в своей жизни и на работе применяют ПНД то и дети «захотят», а если родители имеют бизнес «купи-продай» или резиновой палкой машут на несанкционированных митингах, то их дети «нехотят» и «непонимают».
    
    aleksandros
    11.10.2018 15:25
    #19221667
    Ну да, согласен. Если родители как-то поощрают любознательность, прививают какую-то радость от самого процесса мышления, от нахождения решений, то это здорово.
1. VioletGiraffe
  11.10.2018 11:08
  #19219571
  +2
  Да какая школа. Я всегда любил математику и физику, окончил с отличием технический ВУЗ. Я не могу проследить за некоторыми выкладками в разделе 2, а в разделе 3 окончательно потерялся, дальше могу только читать текст и принимать на веру.
  
  Но самое странное, что я в детстве читал много литературы по физике и естественным наукам — учебники, энциклопедии, научно-популярные книги и журналы, и никогда не слышал о ПНД до недавних дней, когда прочитал на Хабре статью, ответом на которую является данная.

degs
10.10.2018 19:04
#19216669
+1
Исчерпывающее и блестящее обьяснение.

Shkaff
10.10.2018 21:07
#19217285
Теормех был любимым предметом в универе, потому что мало что так красиво выводится из одного принципа, как вся лагранжева механика. А там еще и гамильтонов формализм из основ дифференциальной геометрии, одно удовольствие.

youngmysteriouslight
10.10.2018 21:37
#19217411
система гарантированно перемещается из одного положения в другое!
Не могу проследить, в каком порядке используются кванторы перед переменными «начальное положение» и «конечное положение».

Разверну вопрос. ПНД исходно утверждает, что из того, что система с действием S движется по закону q, следует, что q является (мб, локальным?) минимумом S. То есть в некоторой окрестности q любой закон движения q' должен быть S(q')>S(q).
Про окрестность и локальность прямо не говорится в определении, но далее по тексту подразумевается.

Потом в статье пишется, что для нахождения закона движения из точки A в B (какими бы они ни были) нужно проварьировать действие $\delta S(q, \delta q) = S(q+\delta q) — S(q)$, при этом $\delta q(t_1) = \delta q(t_2) = 0$, то есть производится поиск экстремума на множестве всех законов движения из A в B.

Если это корректное применение ПНД, то, стало быть,
1) либо S определен только на множестве функций q из A в B, (мб, мы работаем с семейством действий, параметризованных начальным и конечным положением)
2) либо в формулировке ПНД нужно указать, что минимизация условная, не по всем возможным законами движения из любой точки в любую, а только по множеству законов, которые имеют общие концы.

Прошу пролить свет на то, что подразумевалось в тексте.

P.S. прошу прощения, не знаю, как формулы оформлять, чтоб MathJax их отрендерил.
1. maisvendoo Автор
  11.10.2018 06:54
  #19218579
  Про окрестность и локальность прямо не говорится в определении, но далее по тексту подразумевается.
  
  Конечно, речь идет о локальном минимуме
  
  мб, мы работаем с семейством действий, параметризованных начальным и конечным положением
  
  Вот эта формулировка представляется мне наиболее приемлемой, так как речь все-таки не о задаче с закрепленными концами
  
  прошу прощения, не знаю, как формулы оформлять, чтоб MathJax их отрендерил
  
  Долго упрашивали создателей ресурса сделать TeX в статьях, и они сделали. А вот до комментов и лички руки у них не дошли. Так что предлагаю использовать Math Text Editor
  1. Druu
    11.10.2018 08:36
    #19218841
    -2
    Вот эта формулировка представляется мне наиболее приемлемой, так как речь все-таки не о задаче с закрепленными концами
    Речь идет именно о задаче с закрепленными концами. Никаких незакрепленных концов нет, почитайте уже учебник наконец.
    
    maisvendoo Автор
    11.10.2018 08:50
    #19218905
    Никакой задачи с закрепленными концами нет
    
    мы работаем с семейством действий, параметризованных начальным и конечным положением
    
    youngmysteriouslight
    11.10.2018 12:03
    #19219927
    Мне это кажется странным. Каждое отдельное действие соответствует задаче с закреплёнными концами. Фактически, в уточнённой Вами постановке решается задача с параметром, в роли параметра выступают начальное и конечное положение.
    
    Вопрос к Druu: если мы говорим-таки о задаче с закреплёнными концами, почему ниже утверждаете, что нет изолированных минимумов, ведь для каждой пары нач/кон положение действие имеет конечное число минимумов.
    
    Druu
    11.10.2018 12:16
    #19220033
    +1
    почему ниже утверждаете, что нет изолированных минимумов
    Не, я такого не утверждал. Я сказал что интересный вопрос — почему они есть :)
    
    Druu
    11.10.2018 12:22
    #19220109
    +1
    Никакой задачи с закрепленными концами нет
    Я, кажется, понял, где у вас мешанина. Давайте забудем на секунду про пнд. Вот есть квадратное уравнение: ax^2 + bx + c = 0;
    
    При решении квадратного уравнения у нас всегда есть конкретные a, b, c — это константы, они даны в конкретной задаче и не меняются. Но если мы решаем случай общего положения, то мы эти известные заданные константы обозначаем как a, b, c. Мы решаем общее уравнение и потом для конкретной задачи подставляем конкретные значения. Еще раз — никто их не меняет, в конкретной задаче они всегда конкретно заданы и известны заранее. Просто при рассмотрении общего случая мы вводим для них обозначения. Это не значит, что данные параметры неизвестны, что-то не закреплено и т.д. — все известно и закреплено.
    
    Аналогичная ситуация с ПНД — в каждом конкретном случае нам известны начало и конец траектории. Но поскольку мы решаем общую задачу, мы просто обозначаем начало и конец за q0 и q1. Еще раз — это не какие-то произвольные начало и конец. q0 и q1 нам известны и однозначно заданы по условию задачи. Никакой неопределенности с ними нет.
    При решении конкретной задаче на всегда известны конкретные q1 и q2 — они всегда нам даны, иначе мы не сможем решить задачу.
    Именно по-этому (потому что q0/q1 нам известны и даны) мы и закрепляем их при вариациях — в противном случае концы в вариациях менялись
    
    maisvendoo Автор
    11.10.2018 13:06
    #19220495
    Но поскольку мы решаем общую задачу, мы просто обозначаем начало и конец за q0 и q1
    
    Разве я не об этом говорю?
    
    Druu
    11.10.2018 15:30
    #19221711
    +1
    Нет, вы о чем-то своем говорите, про то, что начало и конец неизвестны, незакреплены и что-то в этом роде.
    А на деле они вполне себе известны и определены до начала решения задачи.
    И в результате решения вариационной задачи мы получаем конкретную траекторию с этими концами, а не
    
    решение вариационной задачи по принципу наименьшего действия, это не функция, доставляющая минимум действию по Гамильтону, а система дифференциальных уравнений, решая которое таковую функцию можно найти.
    
    maisvendoo Автор
    11.10.2018 15:35
    #19221755
    И в результате решения вариационной задачи мы получаем конкретную траекторию с этими концами
    
    Нет, Вы не правы. Решение вариационной задачи — это дифференциальное уравнение, решая которое можно найти траекторию
    
    Druu
    11.10.2018 15:56
    #19221941
    Нет, Вы не правы. Решение вариационной задачи — это дифференциальное уравнение
    Нет, решение вариационной задачи — это сама траектория.
    Откройте уже учебник и прекратите позориться.
    
    Вариационная задача состоит в том, чтобы найти функцию, на которой функционал дает минимум.
    Не уравнение, решением которой будет эта функция, а сама функция, понимаете?
    
    То что вы предлагаете — это то же самое что в задаче на поиск минимума обычной функции вместо ответа "минимум в точке х = ..." написать: "минимум — это какая-то хрень, которая будет решением у-я bla-bla-bla".
    
    technic93
    12.10.2018 21:00
    #19228767
    почему у вас в уравнении, которое зразу за (10) правая часть равна нулю?
    Потому что вы закрепили граничные условия q(t1) и q(t2).
    У функционала может быть не один минимум (как и у функции).

samsergey
10.10.2018 22:51
#19217621
Отличная статья, но по правилам ведения дискуссии следовало бы дать высказаться до конца автору материала, с которого она началась, прежде чем обрушиваться на неё с критикой. Смею предположить, что это была классическая интрига — создать видимость противоречия, чтобы потом показать как стройная теория красиво исправляет умышленно допущенную ошибку. Именно на таких кажущихся парадоксах строится популярная литература, и даже хорошие курсы. На создании и решении "проблем там, где их нет" строится обучение, основанное на побуждении к исследованию предмета, вместо заучивания верных постулатов и готовых решений.

Увы, это сильно портит ощущение от представленной "правильной" статьи, она правильная, но неинтересная: вместо дополнения и обогащения материала получился спор и выяснения кто прав на повышенных тонах.
1. maisvendoo Автор
  11.10.2018 07:26
  #19218661
  +1
  Смею предположить, что это была классическая интрига
  
  Автору никто не мешает отыграть свою интригу до конца

BlessYourHeart
11.10.2018 00:04
#19217859
Мне кажется та статья является ярким представителем научпопа. Для меня (гуманитария) все доходчиво и понятно в рамках понимания, что применять полученные в статье знания я не собираюсь.

Отсюда немного странно выискивание блох на таком уровне как это сделано в данной статье. Мне, как забывшему термех сразу после экзаменов, и как ЦА критикуемой статьи, ваши доводы не говорят ничего от слова вообще — я в принципе уже не способен себя заставить всмотреться в эту россыпь формул.

Druu
11.10.2018 08:38
#19218849
Так, собственно, а где разрешение указанного противоречия? Напоминаю, противоречие состоит в том, что у нас есть две траектории, у одной из них действие меньше, чем у второй, но шарик двигается по второй траектории. Почему? Ваша статья никак на этот вопрос не отвечает.
1. maisvendoo Автор
  11.10.2018 08:52
  #19218917
  Твою дивизию… У нас есть две действительных траектории, обе являются локальным минимумом функционала действия, и сравнивать действие на этих траекториях некорректно. В ПНД сравниваются действия на действительной и окольной траекториях, параметризированных относительно начального и конечного положения.
  
  Шарик движется по второй траектории, потому что его толкнули в сторону стенки. Но он движется с постоянной скоростью (до момента удара и после него), а не с переменной, именно потому, что вариант движения с постоянной скоростью обеспечивает минимальное действие.
  
  Но, прошу заметить, что речь идет именно о постоянстве скорости, а не конкретной её величине при таком движении
  1. Druu
    11.10.2018 09:39
    #19219089
    Твою дивизию… У нас есть две действительных траектории, обе являются локальным минимумом
    Теперь вы (почти) назвали правильное слово. Но в вашей статье оно не встречается, потому и парадокс в ней — не разрешен.
    
    Однако, даже так — каким образом в итоге шарик выбирает одну из двух траекторий?
    Если, как вы сказали, траектории параметризованы начальным и конечным положением, то, задав эти положения, мы должны получить одну конкретную траекторию движения. Мы же задаем положения — а получаем много траекторий, по какой из них будет двигаться шарик и почему? В вашей статье ответа нет, а в этом же суть.
    
    И предлагаю шарик заменить маятником, тогда не будет разрывов в скорости.
    
    AC130
    11.10.2018 10:05
    #19219217
    При задании координат в качестве краевых условий шарик может двигаться по любой траектории, но каждая эта траектория будет удовлетворять ПНД. Краевые условия в данном случае задают семейство возможных решений. Аналогия: у натянутой струны тоже фиксированы краевые условия, однако решений для волнового уравнения бесконечно много, они отличаются амплитудой.
    
    Druu
    11.10.2018 10:06
    #19219237
    При задании координат в качестве краевых условий шарик может двигаться по любой траектории, но каждая эта траектория будет удовлетворять ПНД.
    Нет, после подстановки краевых условий ПНД удовлетворяет только одна траектория (в данном случае, по крайней мере) — та, где шарик двигается. Стоящий шарик не удовлетворяет ПНД.
    
    Аналогия: у натянутой струны тоже фиксированы краевые условия, однако решений для волнового уравнения бесконечно много, они отличаются амплитудой.
    В итоге-то струна и двигается одновременно со всеми возможными амплитудами. А шарик, определенно, либо стоит, либо катится :)
    
    AC130
    11.10.2018 10:22
    #19219317
    "Стоящий шарик не удовлетворяет ПНД." — докажите формулами. :)
    В некоторых случаях да, краевые условия могут однозначно задать траекторию. Однако в случае x(t1) = x(t2) траекторий две: шарик отправляется в стену и отражается от неё или стоит на месте. И, к слову, шарик не выбирает траекторию по краевым условиям, траектория задается однозначно полным заданием начальных фазовых координат, т.е. в данном примере координаты и скорости.
    
    А про струну, очевидно, имелся в виду случай с рассмотрением одной моды. Не стоит пытаться подменять понятия.
    
    Druu
    11.10.2018 12:28
    #19220151
    "Стоящий шарик не удовлетворяет ПНД." — докажите формулами. :)
    Если ваш шарик двигается в начальной точке (ну то есть вы его толкнули), то второй конец траектории не будет в момент t2, он будет в момент t1+dt, и местоположение шарика в этой точке нам известно — это q(t0+dt) = q0 + q'(0)*dt != q(t0) при ненулевом q'(0).
    
    И, к слову, шарик не выбирает траекторию по краевым условиям, траектория задается однозначно полным заданием начальных фазовых координат, т.е. в данном примере координаты и скорости.
    Вообще нет, именно по краевым условиям траектория и определяется. У вас в задаче есть начало и конец траектории — и это все свободные параметры задачи. Никакой скорости там нет. Другое дело, что, имея скорость, вы можете определить второй конец траектории и потом уже решить задачу.
    
    AC130
    11.10.2018 14:36
    #19221299
    Стоящий шарик — это тот шарик, который не двигается.
    
    Нет, не определяется. Одному значению скорости соответствует одно значение координаты на втором конце траектории. Одному значению координаты соответствуют разные скорости (см пример со струной)
    
    Druu
    11.10.2018 15:34
    #19221741
    Нет, не определяется.
    Ну как не определяется, если определяется. Я выше даже указал, как определяется.
    
    Одному значению координаты соответствуют разные скорости (см пример со струной)
    При чем тут струна вообще? Это просто некорректная аналогия, забудьте про нее.
    
    AC130
    11.10.2018 22:02
    #19223735
    Ну как не определяется, если определяется. Я выше даже указал, как определяется.
    
    Одним и тем же краевым условиям соответствует два решения задачи: стоящий шарик и шарик, который двигался. Вот и не определяется. Заранее предупреждаю, что у стоящего шарика q'(0) = 0, и для любого t q'(t) = 0
    
    При чем тут струна вообще? Это просто некорректная аналогия, забудьте про нее.
    
    Вполне корректная аналогия. Одному дифуру (а ПНД, по факту, тоже приводит к системе дифуров) соответствует более одного решения при задании краевых условий.
    
    maisvendoo Автор
    11.10.2018 11:57
    #19219875
    Стоящий шарик не удовлетворяет ПНД
    
    Покажите, почему не удовлетворяет
    
    С точки зрения законов классической механики шарик покоящийся, и шарик равномерно летящий в сторону стенки — состояния эквивалентные, описываемые одним и тем же дифференциальным уравнением
    
    $\ddot x = 0$
    
    которое непосредственно вытекает из ПНД
    Что касается Вашего вопроса, данного ранее, то вот человек уже ответил на него, а я с этим ответом согласен
    
    При задании координат в качестве краевых условий шарик может двигаться по любой траектории, но каждая эта траектория будет удовлетворять ПНД. Краевые условия в данном случае задают семейство возможных решений.
    
    Если хотите побеседовать о маятнике, могу привести пример с маятником, и показать что Ваши рассуждения дрейфуют уже в сторону чистой софистики
    
    Druu
    11.10.2018 12:32
    #19220209
    Покажите, почему не удовлетворяет
    Потому что ПНД содержит краевые условия, и если шарик не удовлетворяет краевым условиям (а стоящий шарик — не удовлетворяет, см. выше), то и полученная траектория не будет удовлетворять ПНД.
    ПНД удовлетворяет только та траектория, которая проходит через заранее известные начало и конец.
    
    maisvendoo Автор
    11.10.2018 13:13
    #19220579
    +1
    ПНД удовлетворяет только та траектория, которая проходит через заранее известные начало и конец
    
    ПДН удовлетворяет любая траектория, обращающая уравнение Лагранжа в верное равенство. А уравнение Лагранжа непосредственно вытекает из ПНД. Траектория покоящегося шарика уравнению Лагранжа удовлетворяет, значит соответсвует ПНД. Точка
    
    Druu
    11.10.2018 15:36
    #19221777
    ПДН удовлетворяет любая траектория, обращающая уравнение Лагранжа в верное равенство.
    А такая траектория только одна, все верно.
    
    Траектория покоящегося шарика уравнению Лагранжа удовлетворяет
    Нет, не удовлетворяет. У вас в у-е Лагранжа фиксируются концы, траектория должна через эти концы проходить, или решением не является. Траектория покоящегося шарика не проходит через точку q0 + q'dt, с-но, не является решением.
    
    maisvendoo Автор
    11.10.2018 16:00
    #19221969
    А такая траектория только одна,
    
    Что...?
    
    $m\,\ddot x + c\,x = 0$
    – уравнение Лагранжа для колебаний маятника.
    
    Берем функцию
    
    Проверяем
    
    Верно? Верно. Берем другую функцию
    
    $x = \sin\left(\sqrt{\frac{c}{m}} \, t\right)$
    Проверяем
    
    $\ddot x = -\frac{c}{m}\,\sin\left(\sqrt{\frac{c}{m}} \, t\right)$
    $-c\,\sin\left(\sqrt{\frac{c}{m}} \, t\right) + c\, \sin\left(\sqrt{\frac{c}{m}} \, t\right) = 0$
    Верно? Верно. Я же нашел две функции, удовлетворяющие одному и тому же дифференциальному уравнению.
    
    Открою Вам секрет, только Вы никому…! Таких функций… бесконечно много!
    
    Druu
    11.10.2018 16:02
    #19221993
    Верно? Верно. Я же нашел две функции, удовлетворяющие одному и тому же дифференциальному уравнению.
    Погодите, вы решаете вариационную задачу, а в вариационной задаче у вас есть краевые условия. Чтобы быть решением этой задачи — траектория должна удовлетворять этим условиям.
    просто любая траектория не подойдет, извините.
    
    И, да, на самом деле можно построить пример, в котором траекторий будет много, но это никак не связано с рассматриваемой ситуацией, и тем, что вы тут под "бесконечным числом траекторий" подразумеваете, по-этому можно данный нюанс опустить.
    
    maisvendoo Автор
    11.10.2018 16:47
    #19222303
    по-этому можно данный нюанс опустить
    
    потому что Вам так хочется?
    
    Druu
    11.10.2018 17:28
    #19222535
    Нет, потому что это не имеет отношения к предмету обсуждения.
    
    technic93
    12.10.2018 21:06
    #19228793
    Вы о чём? Покоящийся шарик удовлетворяет краевым условиям q(t1)=q(t2).
    
    maisvendoo Автор
    11.10.2018 14:59
    #19221485
    +1
    И предлагаю шарик заменить маятником, тогда не будет разрывов в скорости
    
    Извольте.
    
    Будем говорить не о маятнике в чистом виде, а об заменяющей его эквивалентной системе — точке, совершающей одномерное движение под действием восстанавливающей силы, линейно зависящей от положения. Функция Лагранжа для такой системы имеет вид
    
    $L(x,\,\dot x) = \frac{m\,\dot x^2}{2} - \frac{c\,x^2}{2}$
    Если Вам так хочется, зададим краевые условия
    
    $x(t_1) = x(t_2) = 0 \quad(1)$
    Закон движения точки должен быть таким, чтобы выполнялось
    
    $S = \frac{1}{2}\,\int\limits_{t_1}^{t_2} \, \left(m \, \dot x^2 - c\,x^2 \right)\, dt \to \min$
    Варьируем закон движения, а вариацию функционала приравниваем к нулю
    
    $\delta S = \int\limits_{t_1}^{t_2} \, \left(m \, (\dot x + \delta \dot x)^2 - c\,(x + \delta x)^2 \right)\, dt - \int\limits_{t_1}^{t_2} \, \left(m \, \dot x^2 - c\,x^2 \right)\, dt = 0$
    Раскрываем скобки, раскрываем квадраты, отбрасываем бесконечно малые второго порядка и загоняем всё под один интеграл
    
    $\int\limits_{t_1}^{t_2} (m\,\dot x \, \delta\dot x - c\,x\,\delta x)\,dt = 0$
    Учитываем, что $\delta\dot x = \frac{d(\delta x)}{dt}$
    
    $\int\limits_{t_1}^{t_2} \left[m\,\dot x \, d(\delta \dot x) - c\,x\,\delta x\,dt\right] = 0$
    
    Интегрируем по частям первое слагаемое подынтегрального выражения
    
    $m\,\dot x \, \delta x|_{t_1}^{t_2} + \int\limits_{t_1}^{t_2} \left[\left(-m\,\frac{d\dot x}{dt} - c\,x\right)\, \delta x \right]\,dt = 0$
    Учитывая, что
    
    $\delta x(t_1) = \delta x(t_2) = 0$
    имеем
    
    $\int\limits_{t_1}^{t_2} \left[\left(-m\,\ddot x - c\,x\right)\, \delta x \right]\,dt = 0$
    Что, исходя из свойств определенного интеграла и независимости вариации (благо она ещё и одна!), приводит нас к дифференциальному уравнению
    
    $m\,\ddot x + c\,x = 0 \quad (2)$
    Учитывая, что все сделано "по учебнику", который, как Вы смеете утверждать я не понимаю, то где хотя бы один раз применено условие (1)? ПНД дал нам дифференциальное уравнение движения. На этом он может покинуть сцену, так как уже отработал. Теперь мы имеем уже решение задачи о движении рассматриваемой системы, и это всем известное уравнение (2). ПНД гласит, что если закон движения удовлетворяет (2), то этот закон движения доставляет минимум интегралу действия.
    
    Все дальнейшие игры с начальными и краевыми условиями — чистая софистика к ПНД не имеющая никакого отношения.
    
    Arastas
    11.10.2018 15:17
    #19221629
    Согласен. Я вообще всегда думал, что условие вида (1) относится не к нахождению траектории, а к формированию желаемой траеткории. То есть задача нахождения (для меня) звучит так: x(0)=0, v(0)=1, по какой кривой будет двигаться тело (тут v это скорость). У этой задачи единственное решение.
    А задача вида x(0)=x(1)=0 это задача на отыскание начальных условий, при которых тело пришло бы куда надо и когда надо. Для её решения надо сначала решить задачу нахождения траекторий, а потом найти нужные начальные условия, и на втором шаге решений может быть множество.
    Зачем кто-то пытается применить ПНД сразу ко второй задаче — непонятно.
    
    maisvendoo Автор
    11.10.2018 15:25
    #19221671
    +1
    Зачем кто-то пытается применить ПНД сразу ко второй задаче — непонятно
    
    И мне непонятно, а адекватного объяснения этому я не вижу ни в одной портянке комментариев, ни к той статье, ни к этой.
    
    Druu
    11.10.2018 15:53
    #19221917
    -2
    > Учитывая, что все сделано «по учебнику», который, как Вы смеете утверждать я не понимаю, то где хотя бы один раз применено условие (1)?
    
    Так вы же задачу не решили. Решение вариационной задачи — это конкретная траектория, которая доставляет минимум функционалу при заданных начальной и конечной точках. Я не вижу уравнения этой траектории, закончите решение и сами увидите, где будут использованы концы.
    
    > ПНД дал нам дифференциальное уравнение движения. На этом он может покинуть сцену, так как уже отработал.
    
    В смысле отработал?: Ничего он не отработал. Вариационный принцип определяет конкретную траекторию_. Пока вы не получили _конкретную траекторию_ — ничего не отработало.
    
    > ПНД гласит, что если закон движения удовлетворяет (2), то этот закон движения доставляет минимум интегралу действия.
    
    Нет, это ваши выдумки. ПНД гласит, что если заданы два состояния системы в два каких-то момента времени, то траектория между этими состояниями будет локальным минимумом функционала действия.
    Еще раз — факт того, что состояния в начальный и конечный момент времени заданы, явно присутствует в ПНД.
    
    То, что вы полагаете, будто «результатом решения вариационной задачи» являются у-я Лагранжа — это просто ваша шизофрения. Решением вариационной задачи является решение этих самых уравнений. Пока вы не решили у-я Лагранжа — вы и вариационную задачу не решили. Вы просто свели одну задачу к другой.
    
    maisvendoo Автор
    11.10.2018 16:51
    #19222329
    +1
    То, что вы полагаете, будто «результатом решения вариационной задачи» являются у-я Лагранжа — это просто ваша шизофрения
    
    А ну-ка, резко извинитесь за шизофрению! Я не позволял Вам разговаривать со мной в таком тоне
    
    А что да верности решения, так решите это задачу сами, а потом показывайте где я не прав. Вы тут кроме сомнительной игры с дифференциалами пока ни одного соотношения, подтверждающего Ваши измышления не привели
    
    Druu
    11.10.2018 18:36
    #19222913
    > А что да верности решения, так решите это задачу сами, а потом показывайте где я не прав.
    
    Я не говорил, что решение неверное, я говорил, что оно _не закончено_. Вам надо еще решить уравнения и найти конкретную траекторию. Обозначая a = sqrt(c/m), получим x(t) = k1 * sin(at) + k2 * cos(at), теперь надо уточнить граничные условия, для определенности пусть t1 = 0, то есть x(0) = 0, и тогда сразу x(t) = k1 * sin(at)
    а вот с t2 ситуация интереснее, если взять t2 != n*Pi/a (n — целое), то k1 = 0 и x(t) = 0.
    если же t2 = n*Pi/a, то k1 — любое, т.о. решение у-й Лагранжа будет x(t) = k1 * sin(at) для любого k1. Однако, будут ли соответствующие траектории локальными минимумами? Если взять k1 != 0, то для любой окрестности полученной траектории найдется траектория с меньшим действием (достаточно выбрать траекторию с k1' < k1, k1-k1' < e для некоторого малого е), то есть, это не минимумы. С-но, k1 = 0 и x(t) = 0 — единственная экстремальная траектория в обоих случаях.
    
    Как видите, от выписанных у-й Лагранжа до решения исходной вариационной задачи — еще достаточно далеко. И даже от решений у-й Лагранжа может быть далеко, ведь то, что траектория является решением у-й Лагранжа — это необходимое условие локального минимума, но не достаточное. Полученные решения еще надо проверить, и убедиться, что они действительно доставляют локальный минимум функционалу действия.
    
    > А ну-ка, резко извинитесь за шизофрению! Я не позволял Вам разговаривать со мной в таком тоне
    
    Не вижу никаких проблем в моем тоне. Вы сказали бессмыслицу, я на это указал. Какие тут могут быть обиды?
    
    maisvendoo Автор
    11.10.2018 19:50
    #19223241
    если же t2 = n*Pi/a
    
    Как Вы лихо оценили действие, не считая его! Браво. А я вас сильно огорчу, что если Вы потрудитесь посчитать действие для этого случая непосредственно, то оно окажется равно нулю для любого k1, и ваша игра с константой интегрирования теряет смысл?
    
    Druu
    11.10.2018 20:16
    #19223321
    А, ну да, забыл "a" вынести. Но это содержательно ничего не меняет.
    
    maisvendoo Автор
    11.10.2018 20:19
    #19223331
    Только если m = c. В остальных случаях все имеет смысл.
    
    Нет!
    
    Общее решение уравнения (1)
    
    $x(t) = k_1\, \sin(a\,t) + k_2 \, \cos(a\,t)$
    
    Пусть а $t_2 = \frac{\pi\,n}{a}$ . Из краевого условияя получаем
    
    $x(t) = k_1 \, \sin(a\,t)$
    
    При значении кратном полупериоду колебаний может быть любым. Вычисляем действие непосредственно, учитывая всё выше принятое
    
    $S = \frac{1}{2}\,\int\limits_0^{t_2} (m\,\dot x^2 - c\,x^2)\,dt$
    Учтем, что обобщенная скорость равна $\dot x = k_1\,a\,\cos(a\,t)$
    
    $S = \frac{1}{2} \, \int\limits_0^{t_2} \left( m\, k_1^2 \, a^2 \, \cos^2(a\,t) - c\,k_1^2 \, \sin^2(a\,t)\right) \, dt$
    Далее, заменяя одинарный угол на двойной имеем
    
    $S = \frac{k_1^2}{4} \, \int\limits_0^{t_2} \left(m \, a^2 \, (1 + \cos(2\,a\,t)) - c\,(1 - \cos(2\,a\,t))\right) \, dt$
    Берем интеграл
    
    $S = \frac{k_1^2}{4} \, \left[m\,a^2\,(t + \frac{1}{2\,a}\,\sin(2\,a\,t)) - c\,(t - \frac{1}{2\,a}\sin(2\,a\,t)) \right]|_0^{t_2}$
    
    При подстановке пределов имеем
    
    $S = \frac{k_1^2}{4}\,\frac{\pi\,n}{a}\left(m\,a^2 - c\right)$
    НО! Мы же знаем о том, что $a^2 = \frac{c}{m}$ , тогда
    
    $S = \frac{k_1^2}{4}\,\frac{\pi\,n}{a}\left(m\,\frac{c}{m} - c\right) = 0$
    Итого
    
    $S = 0, \quad \forall k_1 \in R$
    
    maisvendoo Автор
    11.10.2018 20:32
    #19223389
    А, ну да, забыл «a» вынести. Но это содержательно ничего не меняет.
    
    Ах забыл! Это как это не меняет — это испаряет Ваши рассуждения о зависимости действия от k1 и красивую игру в эпсилон-окрестности. Из Ваших выкладок, при заданных Вами же краевых условиях вытекает бесконечное количество решений, обращающих действие в ноль. А ну-ка, извольте объяснить сей факт, или ещё раз назовете меня шизофреником?
    
    И чего это вы отредактировали это Ваше «только при m = c», верните на место!
    
    Druu
    11.10.2018 20:43
    #19223429
    Ах забыл! Это как это не меняет — из Ваших выкладок, при заданных Вами же краевых условиях вытекает бесконечное количество решение, обращающих действие в ноль.
    Да так не меняет. Пост ведь не о наличии решений конкретной задачи и не об их виде. Он о том, что если вы выписали у-я Лагранжа — то вы вариационную задачу не решили. Вам еще надо решить сами у-я Лагранжа с соответствующими краевыми условиями, отсеев невозможные решения (в данном случае при k2 != 0), а потом проверить эти решения на тот факт, что они действительно доставляют минимум (в данном случае это так, но при желании можно построить случай, где это не так).
    
    при заданных Вами же краевых условиях
    Не при всех, а только при t2 = nPi/a. Я мог бы ограничиться случаем t2 != nPi/a и было бы решение одно единственное.
    
    Все это только подтверждает мой тезис — задачу надо до конца решать, а не вываливать уравнение и говорить "я решил", как вы это предлагаете делать. Непонятно, что тут может быть непонятного.
    
    И чего это вы отредактировали это Ваше «только при m = c», верните на место!
    Я перепроверил выкладки и понял, что забыл вынести константу, о чем и написал (если не выносить, то ноль будет только когда m = c, с-но). Какая разница, исправлено, или нет?
    
    maisvendoo Автор
    11.10.2018 20:50
    #19223463
    +1
    Не при всех, а только при t2 = nPi/a. Я мог бы ограничиться случаем t2 != nPi/a и было бы решение одно единственное.
    
    Могли бы ограничится, но а как же быть с декларируемой Вами необходимости проверки всех вариантов? Что-то не сходится в Вашей канцелярии.
    
    И Вы все же полезли анализировать этот вариант и сели в лужу, ай-ай-ай. Ну так вы производные брать научитесь, а потом размахивайте тут томами ландалившица.
    
    Какая разница, исправлено, или нет?
    
    Большая, для тех кто читает и складывает мнение о компетенции спорщиков. А так же их чистоплотности.
    
    в данном случае это так, но при желании можно построить случай, где это не так
    
    Ну так предложите этот случай, а мы посмотрим
    
    Давайте-ка объясняйте случай с t2 кратным полупериоду и не юлите!
    
    P.S.: Заметьте, не я предложил задачу с маятником…
    
    Druu
    12.10.2018 07:53
    #19224833
    Могли бы ограничится, но а как же быть с декларируемой Вами необходимости проверки всех вариантов?
    Где я что-то такое декларировал?
    
    И Вы все же полезли анализировать этот вариант и сели в лужу, ай-ай-ай.
    А почему бы и нет? Раз уж краевые не были четко заданы, то разве не имело смысл рассмотреть все варианты, какой смысл ограничиваться одним, удобным? Тем более, согласитесь, кейз интересный и стоит рассмотрения, разве нет?
    
    Ну так вы производные брать научитесь, а потом размахивайте тут томами ландалившица.
    А почему бы и нет? Ошибки в расчетах — вполне нормальное явление, ничего тут постыдного нет, не было и не будет никогда.
    
    P.S.: Заметьте, не я предложил задачу с маятником…
    Задачу с маятником я предложил на замену шарику, потому что она удобнее. С-но то, что задача с отскакивающим шариком от стены неудобна по некоторым причинам, вы, кажется, и сами указывали в соседнем треде, вариант с маятником устраняет эти проблемы, содержательно ничего при этом не меняя.
    
    Ну так предложите этот случай, а мы посмотрим
    
    Ну таки, если открыть Гантмахера, «Лекции по аналитической механики», то выясняется, что действие должно быть стационарным
    Так это очевидно, ведь логико-исторически пнд выводится из у-й Лагранжа, которые выводятся из з-нов Ньютона, а не наоборот.
    
    У вас какие-то проблемы вообще с пониманием предмета дискуссии, или это я свою позицию как-то невнятно доношу?
    
    Еще раз: есть вариационная задача, это когда "дан функционал, даны концы, надо найти траекторию, минимизирующую функционал", есть задача Коши/краевая задача, это когда "дан диффур, даны начальные/краевые условия, надо найти функцию, удовлетворяющую диффуру при заданных начальных/краевых условиях", это все задачи математические. Есть физические задачи — это когда вам дана некая динамическая система и вы должны что-то об этой системе сообщить.
    Эти задачи могут в определенных условиях друг к другу сводиться, но если вы что-то к чему свели — это еще не решение.
    Вам это понятно? Что тут сложного? Если поставлена вариационная задача, то в поле "ответ" вы должны указать в качестве решения искомую траекторию (или множество траекторий), а не какое-то уравнение.
    
    Давайте опять пример с квадратными уравнениями — представьте, что в качестве ответа, вы написали формулы Виета, ну допустим у вас у-е x^2 + 7x + 10 = 0, и вы пишите: x1+x2=-7, x1*x2=10 и говорите: "ну это ответ". Это же бесссмыслица, какой это ответ? Ответом будут конкретные значения x1 и x2.
    
    И Гантмахер называет уравнение (12) из текста моей статьи, условием для этого не только необходимым, но и достаточным.
    Это достаточное условие стационарности, но не достаточное условие минимизации функционала.
    
    А если вы решаете вариационную задачу, то вы ищите именно минимум функционала.
    
    Замечу ещё, что на протяжении всей дискуссии вы упорно игнорируете термин «окольное движение», сравнивая действия на действительных траекториях.
    Сравнение идет по всем траекториям в окрестности прямого пути, вариация является произвольной, никто не говорит, что ваша вариация не должна быть каким-нибудь другим прямым путем, если он вдруг есть. Просто если прямой путь является строгим локальным минимумом, то, действительно, в некоторой окрестности других прямых путей просто не будет и вы будете вынужденно сравнивать только с окольными.
    
    Но если взять ту же задачу с маятником, то в любой окрестности прямого пути будут другие прямые (при соответствующих краевых условиях). Если вы внимательно читали Гантмахера, то вариации f(x) определяются как произвольные семейства f(x, c), дифференцируемые по параметру. Если теперь выбрать прямой путь в виде нулевой траектории, то никто не мешает рассмотреть семейство c*sin(at) в качестве этого семейства. Это будут вполне корректные вариации прямого пути 0, и они все будут тоже прямые.
    
    P.S.: И да, у Вас, очевидно затруднения, с возможностью писать комментарии. Я зашел к Вам в профиль, и исправил эту ситуацию
    Это блокировка на 5 минут, что никак не помешает разговору, так что если вы считаете, что не стоит мне карму апать — то не надо.
    
    maisvendoo Автор
    11.10.2018 22:45
    #19223893
    +1
    Ну таки, если открыть Гантмахера, «Лекции по аналитической механики», то выясняется, что действие должно быть стационарным, то есть для счастья достаточно равенства нулю его вариации. И Гантмахер называет уравнение (12) из текста моей статьи, условием для этого не только необходимым, но и достаточным. Привожу цитаты в виде скринов под спойлером. Особое внимание выделенным местам.
    
    Гантмахер. Лекции по аналитической механике. Глава 3, параграф 16
    
    maisvendoo Автор
    11.10.2018 23:38
    #19224077
    Обратимся и к любимому всеми ландавшицу
    
    Ландау, Лившиц. Теоретическая физика. Том 1: Механика
    
    technic93
    12.10.2018 23:32
    #19229347
    +1
    я не понимаю, то где хотя бы один раз применено условие (1)?
    Тут.
    
    Учитывая, что
    \delta x(t_1) = \delta x(t_2) = 0
    имеем
    
    maisvendoo Автор
    13.10.2018 13:48
    #19230875
    -1
    Разницу между ку и дельта ку смекаем?
  1. Druu
    11.10.2018 09:49
    #19219151
    +1
    Шарик движется по второй траектории, потому что его толкнули в сторону стенки.
    Это-то понятно, только как это следует из ПНД? Мы же об этом говорим. А то, что вы сейчас написали — ну это какая-то очевидная очевидность.
    
    Еще раз, по вашему, если заданы начальное и конечное положение, мы должны получить конкретную траекторию. Но в случае шарика (который все же предлагаю заменить маятником) мы ее не получаем. Как так?
    
    Здесь еще кстати интересный вопрос — почему указанные локальные минимумы действительно будут локальными минимумами? Мы же на самом деле можешь шарик катнуть сильнее или медленнее — непрерывно меняя начальную скорость, т.о. все точки минимумов, кроме той, что соответствует покоящемуся положению, не будут изолированы. С-но и минимумами не будут. Сможете объяснить, почему это не так?:

Druu
11.10.2018 09:37
#19219075
deleted

amarao
11.10.2018 14:22
#19221185
А как оно с квантовой физикой соотносится? Туннелирование, диаграммы Фейманна и т.д.?
1. KonkovVladimir
  11.10.2018 14:30
  #19221255
  Интегралы по траекториям

Scorobey
13.10.2018 08:29
#19230049
+1
Авторский подход к анализу ПНД объяснения и доказательства основаны на решении вариационной задачи. Хорошая статья, а главное: добротный материал для обучения, за что отдельное спасибо.

Принцип наименьшего действия в аналитической механике +29

Предыстория

Не все так просто

1. Определение действия по Гамильтону. Принцип наименьшего действия

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

5. Задача с шариком и стенкой

Выводы и пожелания

Комментарии (65)

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор

maisvendoo Автор