На
Не претендуя на лавры Мотидзуки, я
Кому интересно что получилось, прошу под кат.
Постановка задачи
Начнем с начала. О чем собственно, теорема? Как гласит Википедия (формулировка в английской версии немного более понятна), для взаимно-простых (не имеющих общих делителей) чисел a, b и с, таких что a+b=c, для любого ?>0 существует ограниченное число троек a+b=c, таких что:
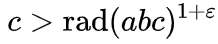
Функция rad называется радикалом, и обозначает произведение простых множителей числа. Например, rad(16) = rad(2*2*2*2) = 2, rad(17) = 17 (17 простое число), rad(18) = rad(2*3*3) = 2*3 = 6, rad(1000000) = rad(2^6 ? 5^6) = 2*5 = 10.
Собственно, суть теоремы в том, что количество таких троек довольно мало. Например, если взять наугад ?=0.2 и равенство 100+27=127: rad(100) = rad(2*2*5*5) = 10, rad(27)=rad(3*3*3)=3, rad(127) = 127, rad(a*b*c) = rad(a)*rad(b)*rad(с) = 3810, 3810^1.2 явно больше 127, неравенство не выполняется. Но бывают и исключения, например для равенства 49 + 576 = 625 условие теоремы выполняется (желающие могут проверить самостоятельно).
Следующий ключевой для нас момент — этих равенств, согласно теореме, ограниченное число. Т.е. это значит, что их все можно просто попытаться перебрать на компьютере. В итоге, это дает нам
Итак, приступим.
Исходный код
Первая версия была написана на Python, и хотя этот язык слишком медленный для подобных расчетов, писать код на нем легко и просто, что удобно для прототипирования.
Получение радикала: раскладываем число на простые множители, затем убираем повторы, преобразуя массив в множество. Затем просто получаем произведение всех элементов.
def prime_factors(n):
factors = []
# Print the number of two's that divide n
while n % 2 == 0:
factors.append(int(2))
n = n / 2
# n must be odd at this point so a skip of 2 ( i = i + 2) can be used
for i in range(3, int(math.sqrt(n)) + 1, 2):
# while i divides n , print i ad divide n
while n % i == 0:
factors.append(int(i))
n = n / i
# Condition if n is a prime number greater than 2
if n > 2:
factors.append(int(n))
return set(factors)
def rad(n):
result = 1
for num in prime_factors(n):
result *= num
return result
Взаимно-простые числа: раскладываем числа на множители, и просто проверяем пересечение множеств.
def not_mutual_primes(a,b,c):
fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c)
return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0
Проверка: используем уже созданные функции, тут все просто.
def check(a,b,c):
S = 1.2 # Eps=0.2
if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c):
print("{} + {} = {} - PASSED".format(a, b, c))
else:
print("{} + {} = {} - FAILED".format(a, b, c))
check(10, 17, 27)
check(49, 576, 625)
Желающие могут поэкспериментировать самостоятельно, скопировав вышеприведенный код в любой онлайн-редактор языка Python. Разумеется, код работает ожидаемо медленно, и перебор всех троек хотя бы до миллиона был бы слишком долгим. Ниже под спойлером есть оптимизированная версия, рекомендуется использовать ее.
Окончательная версия была переписана на С++ с использованием многопоточности и некоторой оптимизации (работать на Си с пересечением множеств было бы слишком хардкорно, хотя вероятно и быстрее). Исходный код под спойлером, его можно скомпилировать в бесплатном компиляторе g++, код работает под Windows, OSX и даже на Raspberry Pi.
// To compile: g++ abc.cpp -O3 -fopenmp -oabc
#include <string.h>
#include <math.h>
#include <stdbool.h>
#include <stdint.h>
#include <stdio.h>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <time.h>
typedef unsigned long int valType;
typedef std::vector<valType> valList;
typedef std::set<valType> valSet;
typedef valList::iterator valListIterator;
std::vector<valList> valFactors;
std::vector<double> valRads;
valList factors(valType n) {
valList results;
valType z = 2;
while (z * z <= n) {
if (n % z == 0) {
results.push_back(z);
n /= z;
} else {
z++;
}
}
if (n > 1) {
results.push_back(n);
}
return results;
}
valList unique_factors(valType n) {
valList results = factors(n);
valSet vs(results.begin(), results.end());
valList unique(vs.begin(), vs.end());
std::sort(unique.begin(), unique.end());
return unique;
}
double rad(valType n) {
valList f = valFactors[n];
double result = 1;
for (valListIterator it=f.begin(); it<f.end(); it++) {
result *= *it;
}
return result;
}
bool not_mutual_primes(valType a, valType b, valType c) {
valList res1 = valFactors[a], res2 = valFactors[b], res3; // = valFactors[c];
valList c12, c13, c23;
set_intersection(res1.begin(),res1.end(), res2.begin(),res2.end(), back_inserter(c12));
if (c12.size() != 0) return false;
res3 = valFactors[c];
set_intersection(res1.begin(),res1.end(), res3.begin(),res3.end(), back_inserter(c13));
if (c13.size() != 0) return false;
set_intersection(res2.begin(),res2.end(), res3.begin(),res3.end(), back_inserter(c23));
return c23.size() == 0;
}
int main()
{
time_t start_t, end_t;
time(&start_t);
int cnt=0;
double S = 1.2;
valType N_MAX = 10000000;
printf("Getting prime factors...\n");
valFactors.resize(2*N_MAX+2);
valRads.resize(2*N_MAX+2);
for(valType val=1; val<=2*N_MAX+1; val++) {
valFactors[val] = unique_factors(val);
valRads[val] = rad(val);
}
time(&end_t);
printf("Done, T = %.2fs\n", difftime(end_t, start_t));
printf("Calculating...\n");
#pragma omp parallel for reduction(+:cnt)
for(int a=1; a<=N_MAX; a++) {
for(int b=a; b<=N_MAX; b++) {
int c = a+b;
if (c > pow(valRads[a]*valRads[b]*valRads[c], S) && not_mutual_primes(a,b,c)) {
printf("%d + %d = %d\n", a,b,c);
cnt += 1;
}
}
}
printf("Done, cnt=%d\n", cnt);
time(&end_t);
float diff_t = difftime(end_t, start_t);
printf("N=%lld, T = %.2fs\n", N_MAX, diff_t);
}
Для тех кому лень устанавливать компилятор С++, приведена слегка оптимизированная Python-версия, запустить которую можно в любом онлайн редакторе (я использовал https://repl.it/languages/python).
from __future__ import print_function
import math
import time
import multiprocessing
prime_factors_list = []
rad_list = []
def prime_factors(n):
factors = []
# Print the number of two's that divide n
while n % 2 == 0:
factors.append(int(2))
n = n / 2
# n must be odd at this point so a skip of 2 ( i = i + 2) can be used
for i in range(3, int(math.sqrt(n)) + 1, 2):
# while i divides n , print i ad divide n
while n % i == 0:
factors.append(int(i))
n = n / i
# Condition if n is a prime number greater than 2
if n > 2:
factors.append(int(n))
return factors
def rad(n):
result = 1
for num in prime_factors_list[n]:
result *= num
return result
def not_mutual_primes(a,b,c):
fa, fb, fc = prime_factors_list[a], prime_factors_list[b], prime_factors_list[c]
return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0
def calculate(N):
S = 1.2
cnt = 0
for a in range(1, N):
for b in range(a, N):
c = a+b
if c > (rad_list[a]*rad_list[b]*rad_list[c])**S and not_mutual_primes(a, b, c):
print("{} + {} = {}".format(a, b, c))
cnt += 1
print("N: {}, CNT: {}".format(N, cnt))
return cnt
if __name__ == '__main__':
t1 = time.time()
NMAX = 100000
prime_factors_list = [0]*(2*NMAX+2)
rad_list = [0]*(2*NMAX+2)
for p in range(1, 2*NMAX+2):
prime_factors_list[p] = set(prime_factors(p))
rad_list[p] = rad(p)
calculate(NMAX)
print("Done", time.time() - t1)
Результаты
Троек a,b,c действительно очень мало.
Некоторые результаты приведены ниже:
N=10: 1 «тройка», время выполнения <0.001c
1 + 8 = 9
N=100: 2 «тройки», время выполнения <0.001c
1 + 8 = 9
1 + 80 = 81
N=1000: 8 «троек», время выполнения <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625
N=10000: 23 «тройки», время выполнения 2с
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
3 + 125 = 128
5 + 1024 = 1029
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
49 + 576 = 625
1331 + 9604 = 10935
81 + 1250 = 1331
125 + 2187 = 2312
243 + 1805 = 2048
289 + 6272 = 6561
625 + 2048 = 2673N=100000: 53 «тройки», время выполнения 50c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
49 + 576 = 625
49 + 16335 = 16384
73 + 15552 = 15625
81 + 1250 = 1331
121 + 12167 = 12288
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
1331 + 9604 = 10935
1625 + 16807 = 18432
28561 + 89088 = 117649
28561 + 98415 = 126976
3584 + 14641 = 18225
6561 + 22000 = 28561
7168 + 78125 = 85293
8192 + 75843 = 84035
36864 + 41261 = 78125При N=1000000 имеем всего лишь 102 «тройки», полный список приведен под спойлером.
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
1 + 137780 = 137781
1 + 156249 = 156250
1 + 229375 = 229376
1 + 263168 = 263169
1 + 499999 = 500000
1 + 512000 = 512001
1 + 688127 = 688128
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
5 + 177147 = 177152
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
13 + 421875 = 421888
17 + 140608 = 140625
25 + 294912 = 294937
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
43 + 492032 = 492075
47 + 250000 = 250047
49 + 576 = 625
49 + 16335 = 16384
49 + 531392 = 531441
64 + 190269 = 190333
73 + 15552 = 15625
81 + 1250 = 1331
81 + 123823 = 123904
81 + 134375 = 134456
95 + 279841 = 279936
121 + 12167 = 12288
121 + 255879 = 256000
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
128 + 109375 = 109503
128 + 483025 = 483153
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
338 + 390625 = 390963
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
864 + 923521 = 924385
1025 + 262144 = 263169
1331 + 9604 = 10935
1375 + 279841 = 281216
1625 + 16807 = 18432
2197 + 583443 = 585640
2197 + 700928 = 703125
3481 + 262144 = 265625
3584 + 14641 = 18225
5103 + 130321 = 135424
6125 + 334611 = 340736
6561 + 22000 = 28561
7153 + 524288 = 531441
7168 + 78125 = 85293
8192 + 75843 = 84035
8192 + 634933 = 643125
9583 + 524288 = 533871
10816 + 520625 = 531441
12005 + 161051 = 173056
12672 + 117649 = 130321
15625 + 701784 = 717409
18225 + 112847 = 131072
19683 + 228125 = 247808
24389 + 393216 = 417605
28561 + 89088 = 117649
28561 + 98415 = 126976
28561 + 702464 = 731025
32768 + 859375 = 892143
296875 + 371293 = 668168
36864 + 41261 = 78125
38307 + 371293 = 409600
303264 + 390625 = 693889
62192 + 823543 = 885735
71875 + 190269 = 262144
131072 + 221875 = 352947
132651 + 588245 = 720896
Увы, программа работает все равно медленно, результатов для N=10000000 я так и не дождался, время вычисления составляет больше часа (возможно я где-то ошибся с оптимизацией алгоритма, и можно сделать лучше).
Еще интереснее посмотреть результаты графически:
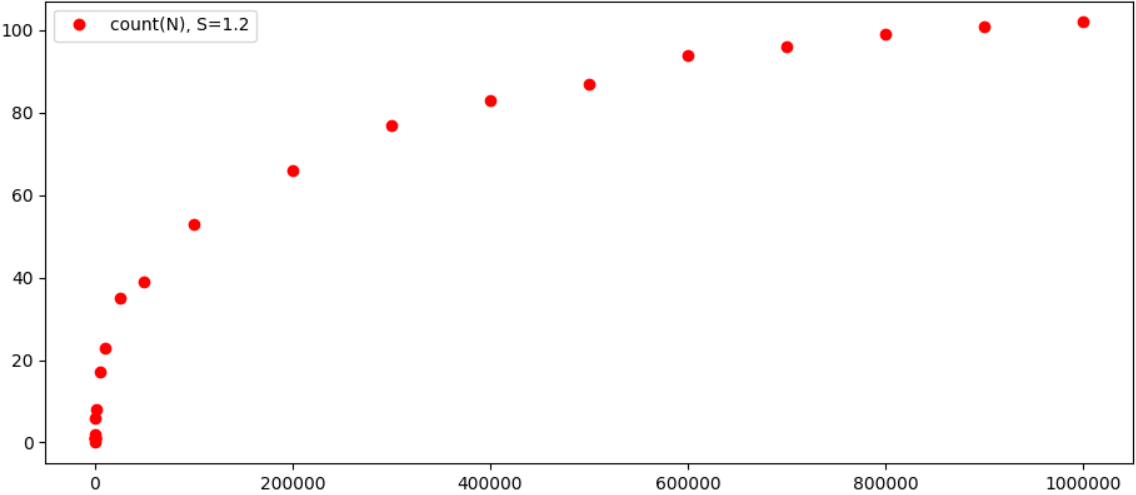
В принципе, вполне очевидно, что зависимость количества возможных троек от N растет заметно медленнее самого N, и вполне вероятно, что результат будет сходиться к какому-то конкретному числу для каждого ?. Кстати, при увеличении ? число «троек» заметно сокращается, например при ?=0.4 имеем всего 2 равенства при N<100000 (1 + 4374 = 4375 и 343 + 59049 = 59392). Так что в целом, похоже что теорема действительно выполняется (ну и наверное ее уже проверяли на компьютерах помощнее, и возможно, все это уже давно посчитано).
Желающие могут поэкспериментировать самостоятельно, если у кого будут результаты для чисел 10000000 и выше, я с удовольствием добавлю их к статье. Разумеется, было бы интересно «досчитать» до того момента, когда множество «троек» совсем перестанет расти, но это может занять реально долгое время, скорость расчета похоже зависит от N как N*N (а может и N^3), и процесс весьма долгий. Но тем не менее, удивительное рядом, и желающие вполне могут присоединиться к поиску.
Правка: как подсказали в комментариях, в Википедии таблица с результатами уже есть — в диапазоне N до 10^18 количество «троек» все же растет, так что «конец» множества пока не найден. Тем интереснее — интрига пока сохраняется.
Комментарии (29)

Sdima1357
20.10.2018 00:04Статья конечно забавная, но ничего и не доказывает. То что 2020 года еще никогда не было, не доказывает что его и не будет…

DmitrySpb79 Автор
20.10.2018 00:06Я на «доказательство» и не претендовал :) Просто было интересно проверить, что получается…

artyomtch
20.10.2018 00:31Наверное, стоит еще раз подчеркнуть, что «rad(a*b*c) = rad(a)*rad(b)*rad(с)» справедливо лишь для взаимнопростых (a,b,c), а не для любой тройки. Я когда прочитал эту строку, то первой мыслью было: «Это неверно!», и лишь второй мыслью было «Ах, да, мы же о взаимнопростых числах...» (но о том было написано двумя абзацами выше).
Но вообще забавно :)
DmitrySpb79 Автор
20.10.2018 09:22Да, взаимная простота чисел явяляется одним из условий теоремы, которое явно указано.

Refridgerator
20.10.2018 05:54В принципе, вполне очевидно, что зависимость количества возможных троек от N растет заметно медленнее самого N, и вполне вероятно, что результат будет сходиться к какому-то конкретному числу для каждого ?
Это ничего не значит. Логарифм числа тоже растёт медленнее, однако его предел в бесконечности равен бесконечности.
maximw
20.10.2018 12:03Именно, на графике монотонно возрастающая функция. И вывод на основе только этого графика, что функция неограниченна, был бы более интуитивно логичен (хотя был бы так же необоснован).

Refridgerator
22.10.2018 11:05Но если функция возрастает как гипербола, то предел будет. Если посмотреть на их производные
(log(x))?=1/x
(1/x)?=-1/x?
то можно предположить, что для наличия предела производная функции должна затухать быстрее, чем 1/х.
DmitrySpb79 Автор
22.10.2018 12:34Тут тема интересная. Как говорит теорема, множество «троек» должно быть ограничено, но как подсказали в комментариях, в Википедии уже есть результаты — пока проверили до 10^18 и «конца» пока не нашли. С другой стороны, может «конец» лежит где-то в районе чисел типа 10^1000, хз.
Так что вопрос открытый, и интрига остается.

Refridgerator
20.10.2018 06:03Мало кому приходит в голову, что abc-гипотеза может быть и ошибочной. Не все гипотезы от великих математиков подтверждаются.

Imposeren
20.10.2018 06:23Это же математики. Конечно же такая мысль много кому приходила в голову:
www.coolissues.com/mathematics/disprovingtheabcconjecture.html
arxiv.org/pdf/math/0503401.pdf
forums.xkcd.com/viewtopic.php?t=125159
И в целом опровергнуть гипотезу было бы не менее престижно и ценно. Но существующие «опровержения» пока принимаются не лучше, чем «доказательства».
DmitrySpb79 Автор
20.10.2018 09:27Кстати странно, но я так и не нашел (а может плохо искал) каких-либо результатов численной проверки гипотезы — дошли до конца множества-то в итоге или нет, хз.
И даже странно, что за 5 лет обсуждения на довольно большом ИТ-ресурсе как хабр, никто не решил проверить. Ни у кого случайно суперкомпьютер не простаивает? ;)

mtivkov
20.10.2018 09:41А не лучше ли было бы не раскладывать a и b на множители, а формировать их из заранее известных простых множителей?
Ну, т.е. понятно, что это лучше для скорости, но немного сложнее алгоритм.
DmitrySpb79 Автор
20.10.2018 11:16Идея интересная, да. Но разложение на множители у меня и так кешируется, и считается только 1 раз на каждое число. Самое медленное в рассчете, это расчет пересечения трех множеств для каждого a,b,c.

Deosis
22.10.2018 10:16Если условие a+b=c выполняется, то достаточно проверить на взаимную простоту только одну пару чисел.

Laney1
20.10.2018 11:31какой-то сильно переусложненный код. Радикалы всех чисел можно найти решетом Эратосфена
for (int i = 2; i < N; ++i) if (rad[i] == 1) for (int j = i; j < N; j += i) rad[j] *= i;
а проверку not_mutual_primes — просто вычисляя gcd, никакое пересечение множеств тут не нужно.

DmitrySpb79 Автор
20.10.2018 11:45Спасибо за идею.
Радикалы не проблема, они вычисляются быстро (меньше 1% от всего времени).
Попробовал в Python-прототипе заменить пересечение множеств на условие gcd(a,b) == gcd(b,c) == gcd(a,c) == 1 — быстрее не стало, время примерно то же. Хотя тут есть один плюс — 3 таблицы для gcd 1..N закешировать можно.
Laney1
20.10.2018 12:07еще одна оптимизация — не проходить по всем парам чисел и искать, какие из них взаимно простые, а генерировать сразу взаимно простые. Это тоже можно сделать простым алгоритмом. См. описание, реализация на питоне

DmitrySpb79 Автор
20.10.2018 12:42Так сложно получается. Во-первых, число может раскладываться на несколько повторяющихся простых чисел, например 2*2*2*3*7, значит надо перебирать все такие варианты. Во-вторых, имея А мы можем сгенерировать только взаимно-простое B, а результат С мы все равно должны вычислять и проверять на пересечение с А, В.
В итоге хз будет ли это быстрее, проще таблицу GCD 1 раз вычислить и в памяти держать, тогда вычисление будет линейно О(1).
Laney1
20.10.2018 14:36у меня получается почти в 2 раза быстрее. https://gist.github.com/1a690590b3506a14fef48ce481803056

MikailBag
20.10.2018 12:55Существует быстрый алгориьм поиска нод, делающий только вычитание и деление на 2. Вы писали его?

ripatti
20.10.2018 15:36+2Немного пооптимиздил:
10^6 22сек — 102 тройки
10^7 30мин — 212 троек
Это все в 1 поток на ноутбуке.
Есть еще несколько идей как ускорить, надеюсь 10^8 затащу. Ну и я еще подумаю код сюда сразу скинуть или статью написать — а то много довольно интересных идей всплыло.
Еще у Вас, кстати, на 10^7 переполнение тут:
valRads[a]*valRads[b]*valRads[c]
DmitrySpb79 Автор
20.10.2018 15:41Спасибо за правку, да, для больших чисел тип в typedef нужно будет поменять.
В виде отдельной статьи будет даже интереснее :)
PS: 212 — интересный результат, пока неясно, уменьшается скорость роста количества троек от N или нет.
vdvvdv
20.10.2018 16:12
Там есть табличка. en.wikipedia.org/wiki/Abc_conjecture
DmitrySpb79 Автор
20.10.2018 20:01О, спасибо, интересно. Пропустил ее как-то. Добавил ссылку в статью.


mphys
Ну на самом деле час это не так уж и долго :)
DmitrySpb79 Автор
Да, подождать можно было бы конечно, но судя по графику каких-то неожиданностей не обещалось. А вот досчитать до момента когда новые тройки ABC вообще перестанут появляться, было бы интересно, судя по теореме такое должно быть.