Вычисляем «магические квадраты» с помощью GPU / forpes.ru

Главная
Вычисляем «магические квадраты» с помощью GPU

Вычисляем «магические квадраты» с помощью GPU +20

29.09.2018 19:54

DmitrySpb79 28 3200 Источник

Привет, habr.

Тема «магических квадратов» достаточно интересна, т.к. с одной стороны, они известны еще с древности, с другой стороны, вычисление «магического квадрата» даже сегодня представляет собой весьма непростую вычислительную задачу. Напомним, чтобы построить «магический квадрат» NxN, нужно вписать числа 1..N*N так, чтобы сумма его горизонталей, вертикалей и диагоналей была равна одному и тому же числу. Если просто перебрать число всех вариантов расстановки цифр для квадрата 4х4, то получим 16! = 20 922 789 888 000 вариантов.

Подумаем, как это можно сделать более эффективно.

Для начала, повторим условие задачи. Нужно расставить числа в квадрате так, чтобы они не повторялись, и сумма горизонталей, вертикалей и диагоналей была равна одному и тому же числу.

Легко доказать, что эта сумма всегда одинакова, и вычисляется по формуле для любого n:

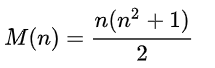
Мы будем рассматривать квадраты 4х4, так что сумма = 34.

Обозначим все переменные черех X, наш квадрат будет иметь такой вид:

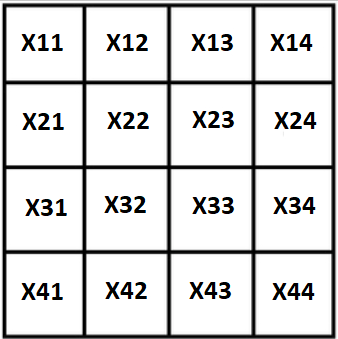
Первое, и очевидное, свойство: т.к. сумма квадрата известна, крайние стоблцы можно выразить через остальные 3:

X14 = S - X11 - X12 - X13

X24 = S - X21 - X22 - X23

...

X41 = S - X11 - X21 - X31

Таким образом, квадрат 4х4 фактически превращается в квадрат 3х3, что уменьшает число вариантов перебора с 16! до 9!, т.е. в 57млн раз. Зная это, приступаем к написанию кода, посмотрим насколько сложен такой перебор для современных компьютеров.

С++ — однопоточный вариант

Принцип программы весьма прост. Берем множество чисел 1..16 и цикл for по этому множеству, это будет х11. Затем берем второе множество, состоящее из первого за исключением числа x11, и так далее.

Примерный вид программы выглядит так:

int squares = 0;
int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
Set mset(digits, digits + N*N);
for (int x11 = 1; x11 <= MAX; x11++) {
  Set set12(mset); set12.erase(x11);
  for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) {
    int x12 = *it12;
    Set set13(set12); set13.erase(x12);
    for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) {
       int x13 = *it13;
       int x14 = S - x11 - x12 - x13;
       if (x14 < 1 || x14 > MAX) continue;
       if (x14 == x11 || x14 == x12 || x14 == x13) continue;
       ...
       int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
       int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
       int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
       if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
         continue;
       // Если числа прошли все проверки на пересечения, то квадрат найден
       printf("%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
       squares++;
   }
}
printf("CNT: %d\n", squares);

Полный текст программы можно найти под спойлером.

Исходный текст целиком

#include <set>
#include <stdio.h>
#include <ctime>
#include "stdafx.h"

typedef std::set<int> Set;
typedef Set::iterator SetIterator;

#define N 4
#define MAX (N*N)
#define S 34

int main(int argc, char *argv[])
{
	// x11 x12 x13 x14 
	// x21 x22 x23 x24 
	// x31 x32 x33 x34 
	// x41 x42 x43 x44 

	const clock_t begin_time = clock();

	int squares = 0;
	int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
	Set mset(digits, digits + N*N);
	for (int x11 = 1; x11 <= MAX; x11++) {
		Set set12(mset); set12.erase(x11);
		for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) {
			int x12 = *it12;
			Set set13(set12); set13.erase(x12);
			for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) {
				int x13 = *it13;
				int x14 = S - x11 - x12 - x13;
				if (x14 < 1 || x14 > MAX) continue;
				if (x14 == x11 || x14 == x12 || x14 == x13) continue;

				Set set21(set13); set21.erase(x13); set21.erase(x14);
				for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) {
					int x21 = *it21;
					Set set22(set21); set22.erase(x21);
					for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) {
						int x22 = *it22;
						Set set23(set22); set23.erase(x22);
						for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) {
							int x23 = *it23, x24 = S - x21 - x22 - x23;
							if (x24 < 1 || x24 > MAX) continue;
							if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue;

							Set set31(set23);
							set31.erase(x23); set31.erase(x24);
							for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) {
								int x31 = *it31;
								Set set32(set31); set32.erase(x31);
								for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) {
									int x32 = *it32;
									Set set33(set32); set33.erase(x32);
									for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) {
										int x33 = *it33, x34 = S - x31 - x32 - x33;
										if (x34 < 1 || x34 > MAX) continue;
										if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue;

										int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34;
										if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue;

										if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 ||
											x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34)
											continue;
										if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 ||
											x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41)
											continue;
										if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 ||
											x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42)
											continue;
										if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 ||
											x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43)
											continue;

										int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
										int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
										int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
										if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
											continue;

										printf("%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
										squares++;
									}
								}
							}
						}
					}
				}
			}
		}
	}
	
	printf("CNT: %d\n", squares);

	float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
	printf("T = %.2fs\n", diff_t);

	return 0;
}

Результат: всего было найдено 7040 вариантов «магических квадратов» 4х4, а время поиска составило 102с.

Кстати интересно проверить, есть ли в списке квадратов тот самый, который изображен на гравюре Дюрера. Разумеется есть, т.к. программа выводит все квадраты размерности 4х4:

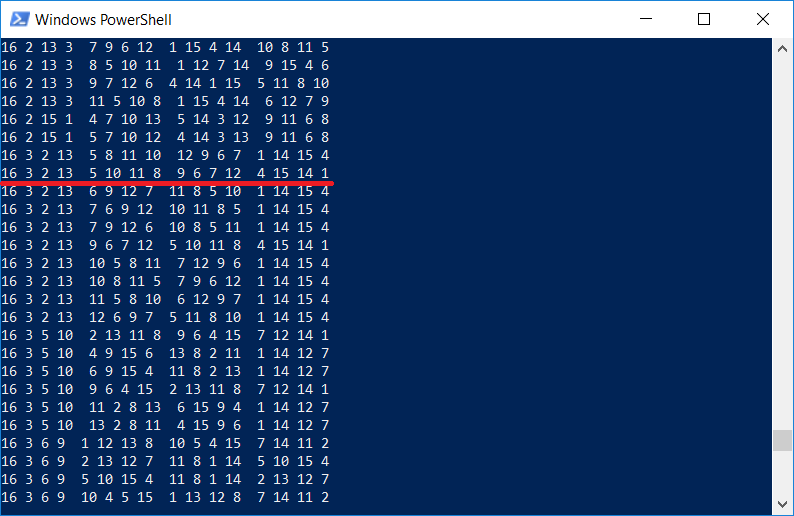
Нельзя не отметить, что Дюрер вставил квадрат в изображение не просто так, цифры 1514 также обозначают год создания гравюры.

Как можно видеть, программа работает (отмечаем задачу как verified at 1514 by Albrecht Durer;), однако время выполнения не так и мало для компьютера с процессором Core i7. Очевидно, что программа выполняется в один поток, и целесообразно задействовать все остальные ядра.

С++ — многопоточный вариант

Переписать программу с использованием потоков в принципе несложно, хотя и немного громоздко. К счастью, есть почти забытый сегодня вариант — использование поддержки OpenMP (Open Multi-Processing). Эта технология существует аж с 1998г, и позволяет директивами процессора указать компилятору, какие части программы выполнять параллельно. Поддержка OpenMP есть и в Visual Studio, так что для превращения программы в многопоточную, достаточно добавить в код лишь одну строку:

int squares = 0;
#pragma omp parallel for reduction(+: squares)
for (int x11 = 1; x11 <= MAX; x11++) {
  ...
}
printf("CNT: %d\n", squares);

Директива #pragma omp parallel for указывает, что следующий цикл for можно выполнять параллельно, а дополнительный параметр squares задает имя переменной, которая будет общей для параллельных потоков (без этого инкремент работает некорректно).

Результат налицо: время выполнения сократилось со 102с до 18с.

Исходный текст целиком

#include <set>
#include <stdio.h>
#include <ctime>
#include "stdafx.h"

typedef std::set<int> Set;
typedef Set::iterator SetIterator;

#define N 4
#define MAX (N*N)
#define S 34

int main(int argc, char *argv[])
{
	// x11 x12 x13 x14 
	// x21 x22 x23 x24 
	// x31 x32 x33 x34 
	// x41 x42 x43 x44 

	const clock_t begin_time = clock();

	int squares = 0;
	#pragma omp parallel for reduction(+: squares)
	for (int x11 = 1; x11 <= MAX; x11++) {
		int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
		Set mset(digits, digits + N*N);
		Set set12(mset); set12.erase(x11);
		for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) {
			int x12 = *it12;
			Set set13(set12); set13.erase(x12);
			for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) {
				int x13 = *it13;
				int x14 = S - x11 - x12 - x13;
				if (x14 < 1 || x14 > MAX) continue;
				if (x14 == x11 || x14 == x12 || x14 == x13) continue;

				Set set21(set13); set21.erase(x13); set21.erase(x14);
				for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) {
					int x21 = *it21;
					Set set22(set21); set22.erase(x21);
					for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) {
						int x22 = *it22;
						Set set23(set22); set23.erase(x22);
						for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) {
							int x23 = *it23, x24 = S - x21 - x22 - x23;
							if (x24 < 1 || x24 > MAX) continue;
							if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue;

							Set set31(set23);
							set31.erase(x23); set31.erase(x24);
							for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) {
								int x31 = *it31;
								Set set32(set31); set32.erase(x31);
								for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) {
									int x32 = *it32;
									Set set33(set32); set33.erase(x32);
									for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) {
										int x33 = *it33, x34 = S - x31 - x32 - x33;
										if (x34 < 1 || x34 > MAX) continue;
										if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue;

										int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34;
										if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue;

										if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 ||
											x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34)
											continue;
										if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 ||
											x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41)
											continue;
										if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 ||
											x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42)
											continue;
										if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 ||
											x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43)
											continue;

										int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
										int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
										int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
										if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
											continue;

										printf("%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
										squares++;
									}
								}
							}
						}
					}
				}
			}
		}
	}
	
	printf("CNT: %d\n", squares);

	float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
	printf("T = %.2fs\n", diff_t);

	return 0;
}

Это гораздо лучше — т.к. задача практически идеально распараллеливается (расчеты в каждой ветви не зависят друг от друга), время меньше примерно в число раз, равное количеству ядер процессора. Но увы, принципиально большего из этого кода не получить, хотя какими-то оптимизациями может и можно выиграть несколько процентов. Переходим к более тяжелой артиллерии, расчетам на GPU.

Вычисления с помощью NVIDIA CUDA

Если не вдаваться в подробности, то процесс вычислений, выполняющийся на видеокарте, можно представить как несколько параллельных аппаратных блоков (blocks), каждый из которых выполняет несколько процессов (threads).

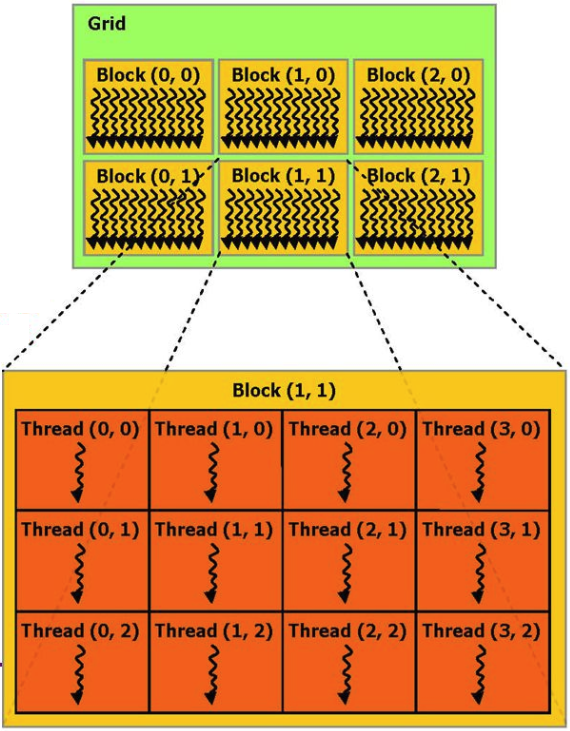
Для примера можно привести пример функции сложения 2х векторов из документации CUDA:

__global__
void add(int n, float *x, float *y)
{
  int index = threadIdx.x;
  int stride = blockDim.x;
  for (int i = index; i < n; i += stride)
      y[i] = x[i] + y[i];
}

Массивы x и y — общие для всех блоков, а сама функция таким образом выполняется одновременно сразу на нескольких процессорах. Ключ тут в параллелизме — процессоры видеокарты гораздо проще чем обычный CPU, зато их много и они ориентированы именно на обработку числовых данных.

Это то, что нам нужно. Мы имеем матрицу чисел X11, X12,..,X44. Запустим процесс из 16 блоков, каждый из которых будет выполнять 16 процессов. Номеру блока будет соответствовать число X11, номеру процесса число X12, а сам код будет вычислять все возможные квадраты с для выбранных X11 и X12. Все просто, но здесь есть одна тонкость — данные нужно не только вычислить, но и передать с видеокарты обратно, для этого в нулевом элементе массива будем хранить число найденных квадратов.

Основной код получается весьма простым:

#define N 4
#define SQ_MAX 8*1024
#define BLOCK_SIZE (SQ_MAX*N*N + 1)

int main(int argc,char *argv[])
{
    const clock_t begin_time = clock();
  
    int *results = (int*)malloc(BLOCK_SIZE*sizeof(int));
    results[0] = 0;

    int *gpu_out = NULL;
    cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int));
    cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice);
    squares<<<MAX, MAX>>>(gpu_out);
    cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost);

    // Print results
    int squares = results[0];
    for(int p=0; p<SQ_MAX && p<squares; p++) {
        int i = MAX*p + 1;
        printf("[%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d]\n", 
                results[i], results[i+1], results[i+2], results[i+3], 
                results[i+4], results[i+5], results[i+6], results[i+7],
                results[i+8], results[i+9], results[i+10], results[i+11],
                results[i+12], results[i+13], results[i+14], results[i+15]);
    }
    printf ("CNT: %d\n", squares);
  
    float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
    printf("T = %.2fs\n", diff_t);
  
    cudaFree(gpu_out);
    free(results);
  
    return 0;
}

Мы выделяем блок памяти на видеокарте с помощью cudaMalloc, запускаем функцию squares, указав ей 2 параметра 16,16 (число блоков и число потоков), соответствующие перебираемым числам 1..16, затем копируем данные обратно через cudaMemcpy.

Сама функция squares по сути повторяет код из предыдущей части, с той разницей, что приращение количества найденных квадратов делается с помощью atomicAdd — это гарантирует что переменная будет корректно изменяться при одновременных обращениях.

Исходный код целиком

// Compile:
// nvcc -o magic4_gpu.exe magic4_gpu.cu

#include <stdio.h>
#include <ctime>

#define N 4
#define MAX (N*N)
#define SQ_MAX 8*1024
#define BLOCK_SIZE (SQ_MAX*N*N + 1)
#define S 34

// Magic square:
// x11 x12 x13 x14 
// x21 x22 x23 x24 
// x31 x32 x33 x34 
// x41 x42 x43 x44 
 
__global__ void squares(int *res_array) {
	int index1 = blockIdx.x, index2 = threadIdx.x;
	if (index1 + 1 > MAX || index2 + 1 > MAX) return;

	const int x11 = index1+1, x12 = index2+1;
	for(int x13=1; x13<=MAX; x13++) { 
		if (x13 == x11 || x13 == x12)
			continue;
		int x14 = S - x11 - x12 - x13;
		if (x14 < 1 || x14 > MAX) continue;
		if (x14 == x11 || x14 == x12 || x14 == x13)
			continue;
		for(int x21=1; x21<=MAX; x21++) { 
			if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14)
				continue;
			for(int x22=1; x22<=MAX; x22++) {
				if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21)
					continue;
				for(int x23=1; x23<=MAX; x23++) {
					int x24 = S - x21 - x22 - x23;
					if (x24 < 1 || x24 > MAX) continue;
					if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22)
						continue;
					if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23)
						continue;
					for(int x31=1; x31<=MAX; x31++) { 
						if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 ||  x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24)
							continue;
						for(int x32=1; x32<=MAX; x32++) {
							if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31)
								continue;
							for(int x33=1; x33<=MAX; x33++) {
								int x34 = S - x31 - x32 - x33;
								if (x34 < 1 || x34 > MAX) continue;
								if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32)
									continue;
								if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33)
									continue;

								const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34;
								if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) 
									continue;
								if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 ||
									x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34)
									continue;
								if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 ||
									x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41)
									continue;
								if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || 
									x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42)
									continue;
								if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || 
									x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43)
									continue;
  
								int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
								int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
								int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
								if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
									continue;

								// Square found: save in array (MAX numbers for each square)
								int p = atomicAdd(res_array, 1);
								if (p >= SQ_MAX) continue;

								int i = MAX*p + 1;
								res_array[i]   = x11; res_array[i+1] = x12; res_array[i+2]  = x13; res_array[i+3]  = x14; 
								res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6]  = x23; res_array[i+7]  = x24; 
								res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; 
								res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; 

								// Warning: printf from kernel makes calculation 2-3x slower
								// printf("%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
							}
						}
					}
				}
			}
		}
	}
}

int main(int argc,char *argv[])
{
	int *gpu_out = NULL;
    cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int));

	const clock_t begin_time = clock();

	int *results = (int*)malloc(BLOCK_SIZE*sizeof(int));
	results[0] = 0;
	cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice);
  
    squares<<<MAX, MAX>>>(gpu_out);

    cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost);

	// Print results
	int squares = results[0];
	for(int p=0; p<SQ_MAX && p<squares; p++) {
		int i = MAX*p + 1;
		printf("[%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3],
																		 results[i+4], results[i+5], results[i+6], results[i+7],
																		 results[i+8], results[i+9], results[i+10], results[i+11],
																		 results[i+12], results[i+13], results[i+14], results[i+15]);
	}
	printf ("CNT: %d\n", squares);
  
	float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
	printf("T = %.2fs\n", diff_t);
  
	cudaFree(gpu_out);
	free(results);
  
	return 0;
}

Результат не требует комментариев — время выполнения составило 2.7с, что примерно в 30 раз лучше изначального однопоточного варианта:

Как подсказали в комментариях, можно задействовать еще больше аппаратных блоков видеокарты, так что был испробован вариант из 256 блоков. Изменение кода минимально:

__global__ void squares(int *res_array) {
	int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX;
	...
}

squares<<<MAX*MAX, 1>>>(gpu_out);

Это сократило время еще в 2 раза, до 1.2с. Далее, на каждом блоке можно запустить 16 процессов, что дает наилучшее время 0.44с.

Окончательный вариант кода

#include <stdio.h>
#include <ctime>

#define N 4
#define MAX (N*N)
#define SQ_MAX 8*1024
#define BLOCK_SIZE (SQ_MAX*N*N + 1)
#define S 34

// Magic square:
// x11 x12 x13 x14 
// x21 x22 x23 x24 
// x31 x32 x33 x34 
// x41 x42 x43 x44 
 
__global__ void squares(int *res_array) {
	int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX, index3 = threadIdx.x;
	if (index1 + 1 > MAX || index2 + 1 > MAX || index3 + 1 > MAX) return;

	const int x11 = index1+1, x12 = index2+1, x13 = index3+1;
	if (x13 == x11 || x13 == x12)
		return;
	int x14 = S - x11 - x12 - x13;
	if (x14 < 1 || x14 > MAX) return;
	if (x14 == x11 || x14 == x12 || x14 == x13)
		return;
	for(int x21=1; x21<=MAX; x21++) { 
		if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14)
			continue;
		for(int x22=1; x22<=MAX; x22++) {
			if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21)
				continue;
			for(int x23=1; x23<=MAX; x23++) {
				int x24 = S - x21 - x22 - x23;
				if (x24 < 1 || x24 > MAX) continue;
				if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22)
					continue;
				if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23)
					continue;
				for(int x31=1; x31<=MAX; x31++) { 
					if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 ||  x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24)
						continue;
					for(int x32=1; x32<=MAX; x32++) {
						if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31)
							continue;
						for(int x33=1; x33<=MAX; x33++) {
							int x34 = S - x31 - x32 - x33;
							if (x34 < 1 || x34 > MAX) continue;
							if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32)
								continue;
							if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33)
								continue;

							const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34;
							if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) 
								continue;
							if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 ||
								x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34)
								continue;
							if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 ||
								x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41)
								continue;
							if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || 
								x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42)
								continue;
							if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || 
								x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43)
								continue;
  
							int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
							int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
							int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
							if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
								continue;

							// Square found: save in array (MAX numbers for each square)
							int p = atomicAdd(res_array, 1);
							if (p >= SQ_MAX) continue;

							int i = MAX*p + 1;
							res_array[i]   = x11; res_array[i+1] = x12; res_array[i+2]  = x13; res_array[i+3]  = x14; 
							res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6]  = x23; res_array[i+7]  = x24; 
							res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; 
							res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; 

							// Warning: printf from kernel makes calculation 2-3x slower
							// printf("%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
						}
					}
				}
			}
		}
	}
}

int main(int argc,char *argv[])
{
	int *gpu_out = NULL;
    cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int));

	const clock_t begin_time = clock();

	int *results = (int*)malloc(BLOCK_SIZE*sizeof(int));
	results[0] = 0;
	cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice);
  
    squares<<<MAX*MAX, MAX>>>(gpu_out);

    cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost);

	// Print results
	int squares = results[0];
	for(int p=0; p<SQ_MAX && p<squares; p++) {
		int i = MAX*p + 1;
		printf("[%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3],
																		 results[i+4], results[i+5], results[i+6], results[i+7],
																		 results[i+8], results[i+9], results[i+10], results[i+11],
																		 results[i+12], results[i+13], results[i+14], results[i+15]);
	}
	printf ("CNT: %d\n", squares);
  
	float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
	printf("T = %.2fs\n", diff_t);
  
	cudaFree(gpu_out);
	free(results);
  
	return 0;
}

Скорее всего, это далеко не идеал, например можно запустить еще больше блоков на GPU, но это сделает код более запутанным и сложным для понимания. И разумеется, расчеты даются не «бесплатно» — при загруженном GPU интерфейс Windows начинает заметно подтормаживать, а энергопотребление компьютера увеличивается практически в 2 раза, с 65 до 130Вт.

Правка: как подсказал в комментариях пользователь Bodigrim, для квадрата 4х4 выполняется еще одно равенство: сумма 4х «внутренних» ячеек равна сумме «внешних», она же равна S.

X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = S

Это позволит еще ускорить алгоритм, выразив одни переменные через другие и убрав еще 1-2 вложенных цикла, обновленный вариант кода можно найти в комментарии ниже.

Заключение

Задача нахождения «магических квадратов» оказалась технически весьма интересной, и в то же время непростой. Даже с вычислениями на GPU поиск всех квадратов 5х5 может занять несколько часов, а оптимизацию для поиска магических квадратов размерности 7х7 и выше, еще предстоит сделать.

Математически и алгоритмически, тоже есть несколько нерешенных моментов:

Зависимость количества «магических квадратов» от N. Известно что квадрата 2х2 не существует, квадратов 3х3 существует всего 8 (но по сути 1, остальные его отражения или повороты), квадратов 4х4 как мы выяснили, 7040, но исключение поворотов или отражений в алгоритм пока не добавлено. Для больших размерностей вопрос пока открыт.
Исключение квадратов, являющимися поворотами или отражениями уже найденного.
Скорость и оптимизация алгоритма. К сожалению, потестировать код на суперкомпьютере или хотя бы на NVIDIA Tesla возможности нет, если кто-то может запустить, было бы интересно. Если у кого есть идеи по самому алгоритму, их тоже можно попробовать реализовать. При желании можно даже запустить распределенный проект по поиску квадратов, если конечно наберется достаточно число читаталей ;)

Об анализе и свойствах самих магических квадратов можно написать отдельную статью, если будет интерес.

P.S.: К вопросу, который наверняка последует, «а зачем это надо». С точки зрения расхода электроэнергии вычисление магических квадратов ничем не лучше или хуже вычисления биткоинов, так что почему бы и нет? К тому же, это интересная разминка для ума и интересная задача в области прикладного программирования.

Комментарии (28)

BubaVV
30.09.2018 01:39
#19174479
А можно ли сгенерировать один квадрат (для нечетной стороны это почти тривиально, известным алгоритмом), а потом тасовать строки и столбцы всеми возможными способами?
1. Karpion
  30.09.2018 04:00
  #19174639
  Мне кажется — так мы получим не все возможные квадраты.
1. Prototik
  30.09.2018 05:22
  #19174673
  Диагонали нарушатся.
1. DmitrySpb79 Автор
  30.09.2018 09:29
  #19174797
  -1
  Спасибо за идею, как уже сказали выше, сумма диагоналей не совпадет.

picul
30.09.2018 03:47
#19174629
+2
Спасибо за статью, хорошую задачу подобрали.
1) ИМХО Вы очень зря используете 16 процессоров на 16 потоков. Во-первых, у процессора 32 потока, так что половина из них просто стоят, во-вторых, если у Вас десктопная видеокарта, то процессоров там явно больше тысячи. Странно сравнивать CPU и GPU, задействуя при этом все потоки процессора, и игнорируя большую часть ресурсов видеокарты.
2) Думаю, если Вы откажетесь в CPU реализации от использования std::set, она взлетит как гордый орел.
3) Еще на счет CPU, не думали задействовать векторные инструкции? Все таки без них потенциал не полностью раскрыт.
И укажите, пожалуйста, железо, на котором проводились тесты.
1. DmitrySpb79 Автор
  30.09.2018 09:28
  #19174795
  Спасибо за советы. Железо нормальное: i7 + GeForce 1060, разумеется, выжать можно больше, осталось придумать как :)
  
  Разбиение на 16 потоков и процессов я взял потому, что это легко «ложится» на алгоритм — индекс потока/процесса равен ячейке матрицы. Так-то да, можно больше задействовать.
  
  Без std:set попробую, спасибо, еще кстати некий прирост скорости получился когда заменил int на char, возможно были лишние преобразования типов, или просто кеш эффективнее используется.
1. DmitrySpb79 Автор
  30.09.2018 09:41
  #19174819
  И еще раз спасибо :) Заменил вычисление через 16 блоков и 16 процессов на 256 блоков по 1 процессу, время стало 1.2 вместо 2.6, еще в 2 раза меньше.
  
  Добавил такой вариант в текст.
  
  Я кстати не нашел ответа о максимально допустимом числе cuda-блоков на видеокарте — оно же «железом» должно определяться?
  1. picul
    30.09.2018 12:19
    #19175123
    +1
    Вы можете узнать эти ограничения через cudaGetDeviceProperties. Но они совершенно неадекватные, просто для галочки. На 940MX они составляют 2147483647 x 65536 x 65536, видимо, только для того, что бы какие-то счетчики не переполнились. Так что можно запускать на сколько угодно блоков, просто одновременно будут исполняться только 1280 (на Geforce 1060).
    Кстати, о самом то важном и не сказал, измерять время в CUDA-реализации с помощью clock() — не очень правильно, в CUDA для этого есть cudaEvent_t.

third112
30.09.2018 08:55
#19174751
Если написать универсальную функцию для любого N с обращением к матрице N х N, замедлит ли это программу (м.б. наоборот ускорит)?
1. DmitrySpb79 Автор
  30.09.2018 09:31
  #19174801
  Имхо да, «разворачивание» цикла до простых линейных операций делает код быстрее, так что универсальный вариант будет работать медленнее.

andy_p
30.09.2018 09:20
#19174777
Мне кажется, что с учетом симметрий, число уникальных квадратов должно быть 220 (7040 ? 32).
1. DmitrySpb79 Автор
  30.09.2018 09:35
  #19174807
  А почему 32? Квадратов 3х3 всего 8, но все они отражения или повороты одного, так что возможно надо на 8 делить.
  1. andy_p
    30.09.2018 09:59
    #19174841
    +1
    Нет, 3 на 3 здесь не причем. 32 = 8?4. 8 — за счет поворотов и отражений, 4 — за счет двух внутренних симметрий.
    
    andy_p
    30.09.2018 20:42
    #19176561
    Да, внутренние симметрии позволяют из квадрата с номерами ячеек
    
    1 2 3 4
    5 6 7 8
    9 10 11 12
    13 14 15 16
    
    создать квадрат
    
    6 5 8 7
    2 1 4 3
    14 13 16 15
    10 9 12 11
    
    и квадрат
    
    1 3 2 4
    9 11 10 12
    5 7 6 8
    13 15 14 16
    
    Ну и комбинация двух этих преобразований дает еще один вариант.

Bodigrim

30.09.2018 13:05

#19175237

Я ничего не понимаю в С++, но немного переработал вашу программу, получив ускорение в 300 раз. В одном потоке, на CPU.

Ключевая идея заключается в том, что в магическом квадрате 4х4 помимо вертикалей, горизонталей и диагоналей магическую сумму дает также сумма угловых ячеек и сумма центральных ячеек. Это позволяет намного раньше останавливать перебор вариантов.

Скрытый текст

#include <set>
#include <stdio.h>
#include <ctime>

typedef std::set<int> Set;
typedef Set::iterator SetIterator;

#define N 4
#define MAX (N*N)
#define S 34

int main(int argc, char *argv[])
{
  // x11 x12 x13 x14
  // x21 x22 x23 x24
  // x31 x32 x33 x34
  // x41 x42 x43 x44

  const clock_t begin_time = clock();

  int squares = 0;
  int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
  Set mset(digits, digits + N*N);
  for (int x11 = 1; x11 <= MAX; x11++) {
    Set set14(mset); set14.erase(x11);
    for (SetIterator it14 = set14.begin(); it14 != set14.end(); it14++) {
      int x14 = *it14;
      Set set41(set14); set41.erase(x14);
      for (SetIterator it41 = set41.begin(); it41 != set41.end(); it41++) {
        int x41 = *it41;
        int x44 = S - x11 - x14 - x41;
        if (x44 < 1 || x44 > MAX) continue;
        if (x44 == x11 || x44 == x14 || x44 == x41) continue;
        Set set22(set41); set22.erase(x41); set22.erase(x44);
        for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++){
          int x22 = *it22;
          int x33 = S - x11 - x22 - x44;
          if (x33 < 1 || x33 > MAX) continue;
          if (x33 == x11 || x33 == x14 || x33 == x41 || x33 == x44 || x33 == x22) continue;
          Set set23(set22); set23.erase(x22); set23.erase(x33);
          for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++){
            int x23 = *it23;
            int x32 = S - x14 - x23 - x41;
            if (x32 < 1 || x32 > MAX) continue;
            if (x32 == x11 || x32 == x14 || x32 == x41 || x32 == x44 || x32 == x22 || x32 == x33 || x32 == x23) continue;
            Set set12(set23); set12.erase(x23); set12.erase(x32);
            for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++){
              int x12 = *it12;
              int x13 = S - x11 - x12 - x14;
              if (x13 < 1 || x13 > MAX) continue;
              if (x13 == x11 || x13 == x14 || x13 == x41 || x13 == x44 || x13 == x22 || x13 == x33 || x13 == x23 || x13 == x32 || x13 == x12) continue;
              int x42 = S - x12 - x22 - x32;
              if (x42 < 1 || x42 > MAX) continue;
              if (x42 == x11 || x42 == x14 || x42 == x41 || x42 == x44 || x42 == x22 || x42 == x33 || x42 == x23 || x42 == x32 || x42 == x12 || x42 == x13) continue;
              int x43 = S - x13 - x23 - x33;
              if (x43 < 1 || x43 > MAX) continue;
              if (x43 == x11 || x43 == x14 || x43 == x41 || x43 == x44 || x43 == x22 || x43 == x33 || x43 == x23 || x43 == x32 || x43 == x12 || x43 == x13 || x43 == x42) continue;
              Set set21(set12); set21.erase(x12); set21.erase(x13); set21.erase(x42); set21.erase(x43);
              for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++){
                int x21 = *it21;
                int x31 = S - x11 - x21 - x41;
                if (x31 < 1 || x31 > MAX) continue;
                if (x31 == x11 || x31 == x14 || x31 == x41 || x31 == x44 || x31 == x22 || x31 == x33 || x31 == x23 || x31 == x32 || x31 == x12 || x31 == x13 || x31 == x42 || x31 == x43 || x31 == x21) continue;
                int x24 = S - x21 - x22 - x23;
                if (x24 < 1 || x24 > MAX) continue;
                if (x24 == x11 || x24 == x14 || x24 == x41 || x24 == x44 || x24 == x22 || x24 == x33 || x24 == x23 || x24 == x32 || x24 == x12 || x24 == x13 || x24 == x42 || x24 == x43 || x24 == x21 || x24 == x31) continue;
                int x34 = S - x31 - x32 - x33;
                if (x34 < 1 || x34 > MAX) continue;
                if (x34 == x11 || x34 == x14 || x34 == x41 || x34 == x44 || x34 == x22 || x34 == x33 || x34 == x23 || x34 == x32 || x34 == x12 || x34 == x13 || x34 == x42 || x34 == x43 || x34 == x21 || x34 == x31 || x34 == x24) continue;

                printf("%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
                squares++;
                }
              }
            }
          }
        }
      }
    }

  printf("CNT: %d\n", squares);

  float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
  printf("T = %.2fs\n", diff_t);

  return 0;
}

DmitrySpb79 Автор

30.09.2018 13:20

#19175279

Спасибо, интересно. А как доказывается это свойство, и распространяется ли оно на квадраты большей размерности?

Идея отказаться от Set была, да. Суть использования Set в том, чтобы заведомо не перебирать и не проверять уже повторяющиеся числа, например 1 с 1.

Bodigrim
30.09.2018 13:26
#19175293
Во-первых, x22 + x23 + x32 + x33 = 2S — (x21 + x24 + x31 + x34) = 2S — (2S — (x11 + x14 + x41 + x44)) = x11 + x14 + x41 + x44. Но (x22 + x23 + x32 + x33) + (x11 + x14 + x41 + x44) = 2S как сумма двух диагоналей. Отсюда x22 + x23 + x32 + x33 = x11 + x14 + x41 + x44 = S. Насколько я помню, непосредственно это свойство на квадраты высших порядков не обобщается, но я не специалист.
1. DmitrySpb79 Автор
  30.09.2018 14:21
  #19175473
  Спасибо, добавил ваше описание в текст. Если аналогичный подход сработает для 5х5 и выше, это заметно ускорит поиск.

Bodigrim

30.09.2018 14:52

#19175585

Замена Set на битовую маску дала ускорение еще в 20 раз, программа отрабатывает за пару сотых секунды.

Скрытый текст

#include <set>
#include <stdio.h>
#include <ctime>
// #include "stdafx.h"

typedef std::set<int> Set;
typedef Set::iterator SetIterator;

#define N 4
#define MAX (N*N)
#define S 34

int main(int argc, char *argv[])
{
  // x11 x12 x13 x14
  // x21 x22 x23 x24
  // x31 x32 x33 x34
  // x41 x42 x43 x44

  const clock_t begin_time = clock();

  int squares = 0;
  int mask = 0;
  for (int x11 = 1; x11 <= MAX; x11++) {
    mask += 1 << x11;
    for (int x14 = 1; x14 <= MAX; x14++) {
      if (mask & (1 << x14)) continue;
      mask += 1 << x14;
      for (int x41 = 1; x41 <= MAX; x41++) {
        if (mask & (1 << x41)) continue;
        int x44 = S - x11 - x14 - x41;
        if (x44 < 1 || x44 > MAX) continue;
        if (mask & (1 << x44) || x44 == x41) continue;
        mask += 1 << x41;
        mask += 1 << x44;
        for (int x22 = 1; x22 <= MAX; x22++){
          if (mask & (1 << x22)) continue;
          int x33 = S - x11 - x22 - x44;
          if (x33 < 1 || x33 > MAX) continue;
          if (mask & (1 << x33) || x33 == x22) continue;
          mask += 1 << x22;
          mask += 1 << x33;
          for (int x23 = 1; x23 <= MAX; x23++){
            if (mask & (1 << x23)) continue;
            int x32 = S - x14 - x23 - x41;
            if (x32 < 1 || x32 > MAX) continue;
            if (mask & (1 << x32) || x32 == x23) continue;
            mask += 1 << x23;
            mask += 1 << x32;
            for (int x12 = 1; x12 <= MAX; x12++){
              if (mask & (1 << x12)) continue;
              int x13 = S - x11 - x12 - x14;
              if (x13 < 1 || x13 > MAX) continue;
              if (mask & (1 << x13) || x12 == x13) continue;
              int x42 = S - x12 - x22 - x32;
              if (x42 < 1 || x42 > MAX) continue;
              if (mask & (1 << x42) || x42 == x12 || x42 == x13) continue;
              int x43 = S - x13 - x23 - x33;
              if (x43 < 1 || x43 > MAX) continue;
              if (mask & (1 << x43) || x43 == x12 || x43 == x13 || x43 == x42) continue;
              mask += 1 << x12;
              mask += 1 << x13;
              mask += 1 << x42;
              mask += 1 << x43;
              for (int x21 = 1; x21 <= MAX; x21++){
                if (mask & (1 << x21)) continue;
                int x31 = S - x11 - x21 - x41;
                if (x31 < 1 || x31 > MAX) continue;
                if (mask & (1 << x31) || x31 == x21) continue;
                int x24 = S - x21 - x22 - x23;
                if (x24 < 1 || x24 > MAX) continue;
                if (mask & (1 << x24) || x24 == x21 || x24 == x31) continue;
                int x34 = S - x31 - x32 - x33;
                if (x34 < 1 || x34 > MAX) continue;
                if (mask & (1 << x34) || x34 == x21 || x34 == x24 || x34 == x31) continue;

                printf("%d %d %d %d  %d %d %d %d  %d %d %d %d  %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
                squares++;
                }
              mask -= 1 << x12;
              mask -= 1 << x13;
              mask -= 1 << x42;
              mask -= 1 << x43;
              }
            mask -= 1 << x23;
            mask -= 1 << x32;
            }
          mask -= 1 << x22;
          mask -= 1 << x33;
          }
        mask -= 1 << x41;
        mask -= 1 << x44;
        }
      mask -= 1 << x14;
      }
    mask -= 1 << x11;
    }

  printf("CNT: %d\n", squares);

  float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
  printf("T = %.2fs\n", diff_t);

  return 0;
}

DmitrySpb79 Автор
30.09.2018 14:59
#19175605
А говорите, не знаете C ;)

Респект, отличный результат.

yizraor
30.09.2018 16:50
#19175881
Хе-хех… Есть чрезвычайно простой алгоритм для создания "магических квадратов". Никакого перебора в нём вообще нет. Помню, в детстве у меня была детская энциклопедия по математике (от Аванта+), и в ней был описан алгоритм построения ("Меланхолия и магия в квадрате"). Заболев на 2-м курсе воспалением лёгких, лежал в больничке и, помимо решения японских кроссвордов, в тетрадке писал код на паскале, строящий "магические квадраты" заданной размерности. Неплохо развлёкся :)
Впрочем, переборный способ, наверное, неплох для демонстрации многопоточных техник и вычислений на GPU.
1. DmitrySpb79 Автор
  30.09.2018 21:03
  #19176629
  Да, методы создания квадратов разных размерностей известны еще со средних веков, но здесь-то вопрос был в нахождении всех вариантов.

andy_p
30.09.2018 20:50
#19176591
Кстати, подсчитать общее количество вариантов для квадрата 4x4 можно вообще без компьютера — с помощью головы, бумаги и карандаша где-то за половину часа.

YAnri
30.09.2018 22:20
#19176799
Спасибо, за задачу я попробую сам сделать алгоритм для магического квадрата, а затем прочитаю вашу статью))

vokalbo
01.10.2018 08:17
#19177429
Взял старенький ноут с Core 2 Duo 1.66GHz десятилетней давности, скомпилировал самое первое решение автора под ubuntu 18.04 32-bit gcc 5.4, выкинув одну строчку с #include «stdafx.h», ибо мешалась. Получил T = 309, поставил ключик -O2 для gcc получил уже T~ 85-90. Так что не очень понятно почему i7 так плохо выступил.

Лет десять не программировал, но написал своё решение. Может где ошибся конечно, но без разворачивания циклов ручками и прочей ручной оптимизации, получил время T между 18-19 на всё том же стареньком ноуте, а с ключиком -O2 время было T ~ 4-5. Что я не так понял для однопоточного случая?
своё решение:
#include <stdio.h> #include #define N 4 #define MAX (N*N) #define S ((N)*((N)*(N)+1)/2) int main(int argc,char *argv[]) { const clock_t begin_time = clock(); int squares = 0; struct Ts{ int pole[MAX]; // поле с цифирьками int numb[MAX]; // где стоит каждое число int* ocher[MAX*2]; // какие изменения делались int o; // сколько чисел поменяли int num; // текущее число int last[MAX]; // список предположений int l; // указатель последнего предположения Ts():o(0),num(0),l(0){ for (int i=0;i<MAX;i++) { //начальные значения всё в ноль pole[i]=0; numb[i]=0; ocher[i]=NULL; ocher[i+MAX]=NULL; last[i]=0; } } inline bool set(int m, int n) { ocher[o++] = &numb[n-1]; numb[n-1]=m+1; // запоминаем что модифицировали, между корректными точками ocher[o++] = &pole[m]; pole[m]=n; return check(m); // возможна рекурсия... } inline bool add(int m, int n) { last[l++]=n-1; // записываем куда вернёмся в случае roolback return set(m,n); } inline bool test(int m,int s){ if (m==-1) return s==S; // если пустых ячеек нет, то сумма всех должна равняться заранее известному числу s = S - s; if (s>MAX || s<=0 || numb[s-1]) return false; return set(m,s); // если единственная оставшаяся ячейка проходит проверки записываем в неё правильное значение вне очереди } bool diag1() { // проверяем главную диагональ int m=-1,sum=0; for (int i=0;i<N;i++) { int n=i+i*N; if (pole[n]) sum+=pole[n]; else { if(m==-1) m=n; else return true; // если две пустых ячейки ничего дальше считать не удем, рано. } } return test(m,sum); } bool diag2() { // проверяем другую диагональ int m=-1,sum=0; for (int i=0;i<N;i++) { int n=N-1-i+i*N; if(! pole[n]) { if(m==-1) m=n; else return true; } else sum+=pole[n]; } return test(m,sum); } bool checkS(int s){ // проверяем строку int m=-1,sum=0; for (int i=0;i<N;i++) { int n=i+s*N; if(! pole[n]) { if(m==-1) m=n; else return true; } else sum+=pole[n]; } return test(m,sum); } bool checkH(int h){ // проверяем столец int m=-1,sum=0; for (int i=0;i<N;i++) { int n=h+i*N; if(! pole[n]) { if(m==-1) m=n; else return true; } else sum+=pole[n]; } return test(m,sum); } inline bool check(int m) { // решаем что удем проверять после очередного предположения int s = m/N; int h = m%N; return checkS(s) && checkH(h) && ((h==s)?diag1():((h==N-1-s)?diag2():true)); } int roolback() { // откат предыдущего преположения int lnum=last[--l]; if (num<MAX) numb[num]=0; // текущее значение уже не интересно for (o--;ocher[o]!=&numb[lnum];o--) *ocher[o]=0; //*ocher[o]=0; numb[lnum]--; return lnum; } inline void next() { // следующая позиция цифры numb[num]++; } inline void print() { // печать поля printf("["); for (int i=0;i<MAX-1;i++) printf((i%N==N-1)?"%d ":"%d ",pole[i]); printf("%d]\n",pole[MAX-1]); }; } p; for (;;p.next()) { // не очень красиво, вечный цикл int m = p.numb[p.num]; if (m>=MAX) if (p.num==0) break; // всё конец, все варианты перерали else p.num=p.roolback(); // не смогли для текущего числа найти позицию else if (p.pole[m]==0) { if (p.add(m,++p.num)) { // ставим число в новую позицию while (p.num<MAX && p.numb[p.num]>0) p.num++; // а вдруг мы уже всё поставили? if (p.num==MAX) { p.print();squares++; // новый квадрат p.num=p.roolback(); // ищем следующий } else p.numb[p.num]=-1; // не очень красиво, коменсируем следующий next } else p.num=p.roolback(); // не получилось } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
1. DmitrySpb79 Автор
  01.10.2018 08:22
  #19177435
  Спасибо. Я тоже пробовал, заметно быстрее без std::set, все же медленный он для таких целей.
  
  С первым вариантом, я нашел у себя ошибку, где-то в цикле было char а где-то int, часть времени «съелось» на преобразовании типов. После исправления стало 60с.
1. DmitrySpb79 Автор
  01.10.2018 08:50
  #19177491
  Кстати, перепроверил сейчас еще раз — все еще более запутанно :)
  
  Если в качестве базовой переменной использовать int, время выполнения 100с и 19с в одно и многопоточном варианте. Если заменить int на char, то однопоточный вариант дает 60с, а многопоточный наоборот ухудшается до 34с.
  (Компилятор: Visual Studio 2015)
  
  Думаю, в однопоточном варианте программа с char лучше помещается в кеш, и работает быстрее.

smplcd

02.10.2018 00:33

#19180947

Можно очень просто ускорить вычисление, просто выводя все данные в .txt файл:

#include <set>
#include <stdio.h>
#include <ctime>
#include <fstream>
#include "stdafx.h"

...

int main(int argc, char *argv[])
{
	// x11 x12 x13 x14 
	// x21 x22 x23 x24 
	// x31 x32 x33 x34 
	// x41 x42 x43 x44 

        char *fileName = "magicSquares.txt"
        std::ofstream magicSquares(fileName);
        magicSquares.open(fileName);
        freopen(fileName, "w", stdout);

	const clock_t begin_time = clock();

	int squares = 0;
	int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
	Set mset(digits, digits + N * N);
	for (int x11 = 1; x11 <= MAX; x11++)
       {
	       ...
       }
	
	printf("CNT: %d\n", squares);

	float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
	printf("T = %.2fs\n", diff_t);
        
        magicSquares.close();
       
	return 0;
}