С целью освоения библиотек для работы с нейронными сетями, решим задачу аппроксимации функции одного аргумента используя алгоритмы нейронных сетей для обучения и предсказания.
Вступление
Пусть задана функция f:[x0,x1]->R
Аппроксимируем заданную функцию f формулой
P(x) = SUM W[i]*E(x,M[i])где
- i = 1..n
- M[i] из R
- W[i] из R
- E(x,M) = { 0, при x<M; 1/2, при x=M; 1, при x>M
Очевидно, что при равномерном распределении значений M[i] на отрезке (x0,x1) найдутся такие величины W[i], при которых формула P(x) будет наилучшим образом апроксимировать функцию f(x). При этом, для заданных значений M[i], определённых на отрезке (x0,x1) и упорядоченных по возрастанию, можно описать последовательный алгоритм вычисления величин W[i] для формулы P(x).
А вот и нейросеть
Преобразуем формулу P(x) = SUM W[i]*E(x,M[i]) к модели нейросети с одним входным нейроном, одним выходным нейроном и n нейронами скрытого слоя
P(x) = SUM W[i]*S(K[i]*x + B[i]) + Cгде
- переменная x — "входной" слой, состоящий из одного нейрона
- {K, B} — параметры "скрытого" слоя, состоящего из n нейронов и функцией активации — сигмоида
- {W, C} — параметры "выходного" слоя, состоящего из одного нейрона, который вычисляет взвешенную сумму своих входов.
- S — сигмоида,
при этом
- начальные параметры "скрытого" слоя K[i]=1
- начальные параметры "скрытого" слоя B[i] равномерно распределены на отрезке (-x1,-x0)
Все параметры нейросети K, B, W и C определим обучением нейросети на образцах (x,y) значений функции f.
Сигмоида
Сигмоида — это гладкая монотонная возрастающая нелинейная функция
- S(x) = 1 / (1 + exp(-x)).
Программа
Используем для описания нашей нейросети пакет Tensorflow
# узел на который будем подавать аргументы функции
x = tf.placeholder(tf.float32, [None, 1], name="x")
# узел на который будем подавать значения функции
y = tf.placeholder(tf.float32, [None, 1], name="y")
# скрытый слой
nn = tf.layers.dense(x, hiddenSize,
activation=tf.nn.sigmoid,
kernel_initializer=tf.initializers.ones(),
bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0),
name="hidden")
# выходной слой
model = tf.layers.dense(nn, 1,
activation=None,
name="output")
# функция подсчёта ошибки
cost = tf.losses.mean_squared_error(y, model)
train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost)
Обучение
init = tf.initializers.global_variables()
with tf.Session() as session:
session.run(init)
for _ in range(iterations):
train_dataset, train_values = generate_test_values()
session.run(train, feed_dict={
x: train_dataset,
y: train_values
})
Полный текст
import math
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
x0, x1 = 10, 20 # диапазон аргумента функции
test_data_size = 2000 # количество данных для итерации обучения
iterations = 20000 # количество итераций обучения
learn_rate = 0.01 # коэффициент переобучения
hiddenSize = 10 # размер скрытого слоя
# функция генерации тестовых величин
def generate_test_values():
train_x = []
train_y = []
for _ in range(test_data_size):
x = x0+(x1-x0)*np.random.rand()
y = math.sin(x) # исследуемая функция
train_x.append([x])
train_y.append([y])
return np.array(train_x), np.array(train_y)
# узел на который будем подавать аргументы функции
x = tf.placeholder(tf.float32, [None, 1], name="x")
# узел на который будем подавать значения функции
y = tf.placeholder(tf.float32, [None, 1], name="y")
# скрытый слой
nn = tf.layers.dense(x, hiddenSize,
activation=tf.nn.sigmoid,
kernel_initializer=tf.initializers.ones(),
bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0),
name="hidden")
# выходной слой
model = tf.layers.dense(nn, 1,
activation=None,
name="output")
# функция подсчёта ошибки
cost = tf.losses.mean_squared_error(y, model)
train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost)
init = tf.initializers.global_variables()
with tf.Session() as session:
session.run(init)
for _ in range(iterations):
train_dataset, train_values = generate_test_values()
session.run(train, feed_dict={
x: train_dataset,
y: train_values
})
if(_ % 1000 == 999):
print("cost = {}".format(session.run(cost, feed_dict={
x: train_dataset,
y: train_values
})))
train_dataset, train_values = generate_test_values()
train_values1 = session.run(model, feed_dict={
x: train_dataset,
})
plt.plot(train_dataset, train_values, "bo",
train_dataset, train_values1, "ro")
plt.show()
with tf.variable_scope("hidden", reuse=True):
w = tf.get_variable("kernel")
b = tf.get_variable("bias")
print("hidden:")
print("kernel=", w.eval())
print("bias = ", b.eval())
with tf.variable_scope("output", reuse=True):
w = tf.get_variable("kernel")
b = tf.get_variable("bias")
print("output:")
print("kernel=", w.eval())
print("bias = ", b.eval())Вот что получилось
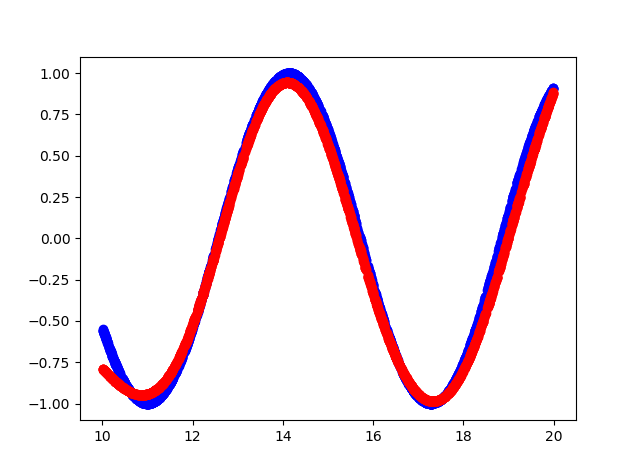
- Синий цвет — исходная функция
- Красный цвет — аппроксимация функции
Вывод консоли
cost = 0.15786637365818024
cost = 0.10963975638151169
cost = 0.08536215126514435
cost = 0.06145831197500229
cost = 0.04406769573688507
cost = 0.03488277271389961
cost = 0.026663536205887794
cost = 0.021445846185088158
cost = 0.016708852723240852
cost = 0.012960446067154408
cost = 0.010525770485401154
cost = 0.008495906367897987
cost = 0.0067353141494095325
cost = 0.0057082874700427055
cost = 0.004624188877642155
cost = 0.004093789495527744
cost = 0.0038146725855767727
cost = 0.018593043088912964
cost = 0.010414039716124535
cost = 0.004842184949666262
hidden:
kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508
0.87283015 1.0875995 0.9677301 0.6194152 ]]
bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006
-13.379829 -20.508204 -14.923473 -19.354435]
output:
kernel= [[ 2.0069902 ]
[-1.0321712 ]
[-0.8878887 ]
[-2.0531905 ]
[ 1.4293027 ]
[ 2.1250408 ]
[-1.578137 ]
[ 4.141281 ]
[-2.1264815 ]
[-0.60681605]]
bias = [-0.2812019]Исходный код
Комментарии (7)

ProLimit
30.10.2018 22:38В условии задачи одно определение E(x,M), а потом вы нигде к нему не возвращаетесь. В этом определении возникают вопросы относительно "...1/2, при x=M… " — есть ли смысл сравнивать два вещественных числа?

dprotopopov Автор
30.10.2018 22:45Вы правы — я сперва определил разрывную в точке M функцию E(x,M) для указании в формуле, а потом быстро заменил её на непрерывную функцию сигмоида S(x) = 1 / (1 + exp(-x)).
Значение 1/2 при x=M я указал для похожести со значением S(0)=1/2.

aamonster
30.10.2018 23:19(подавив желание запостить картинку с троллейбусом)
Но зачем? Проверили ли вы, что нет более простых и удобных методов для этого? (метод наименьших квадратов, само собой)
Нашли ли случаи, когда использование нейронной сети оправдано? (мой опыт: когда мы не знаем, как решать задачу… В данном случае можно подумать о ситуациях, когда приближать надо не суммой, а какой-то более сложной композицией функций)
Исследовали ли устойчивость полученного решения? (вспоминается классика: интерполяция полиномами Лагранжа на равномерной сетке может развалиться, несмотря на "хорошее" поведение функции)
dprotopopov Автор
30.10.2018 23:30+1Цель была обозначена в самом начале статьи — освоение библиотеки работы с нейронной сетью, в большей мере для саморазвития. Полного исследования я не делал.
Запуская программу при разных параметрах (коэффициент переобучения, количество итераций обучения, количество нейронов внутреннего слоя) я получал разные (в том числе не особо удовлетворительные) результаты.
Я и ранее использовал тему аппроксимации функций для статьи habr.com/post/277541
aamonster
31.10.2018 01:11Освоение — дело хорошее, но разобраться в пределах применимости инструмента — сложнее и важнее.


Andy_U
Не могли бы вы пояснить, что математически означает «наилучшим образом апроксимировать функцию»?
dprotopopov Автор
«наилучшим образом» зависит от выбранной методики сравнения двух функций, например среднеквадратичное отклонение, или максимальное отклонение или другая методика сравнения.
Далее для нейросети я использовал cost = tf.losses.mean_squared_error(y, model) — минимизация среднеквадратичного отклонения.