
Современная DDR3 SDRAM. Источник: BY-SA/4.0 by Kjerish
Во время недавнего посещения Музея компьютерной истории в Маунтин-Вью моё внимание привлёк древний образец ферритовой памяти.

Источник: BY-SA/3.0 by Konstantin Lanzet
Я быстро пришёл к выводу, что понятия не имею, как подобные штуки работают. Вращаются ли кольца (нет), и почему через каждое кольцо проходит три провода (я до сих пор не понимаю, как именно они работают). Что ещё более важно, я понял, что очень слабо представляю принцип работы современной динамической RAM!
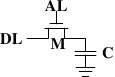
Источник: Цикл Ульриха Дреппера о памяти
Меня особенно интересовало одно из следствий того, как работает динамическая RAM. Получается, что каждый бит данных хранится зарядом (или его отсутствием) на крошечном конденсаторе в микросхеме ОЗУ. Но эти конденсаторы постепенно теряют заряд со временем. Чтобы избежать потери сохранённых данных, они должны регулярно обновляться, чтобы восстановить заряд (если он есть) до первоначального уровня. Этот процесс обновления включает чтение каждого бита, а потом запись его обратно. В процессе такого «обновления» память занята и не может выполнять обычные операции, такие как запись или хранение битов.
Это долго беспокоило меня, и я задался вопросом… можно ли заметить задержку обновления на программном уровне?
Учебная база по обновлению динамической RAM
Каждый модуль DIMM состоит из «ячеек» и «строк», «столбцов», «сторон» и/или «рангов». Эта презентация от Университета штата Юта объясняет номенклатуру. Конфигурацию памяти компьютера можно проверить командой
decode-dimms. Вот пример:$ decode-dimms Size 4096 MB Banks x Rows x Columns x Bits 8 x 15 x 10 x 64 Ranks 2
Нам не нужно разбираться во всей схеме DDR DIMM, мы хотим понять работу только одной ячейки, хранящей один бит информации. А точнее, нас интересует только процесс обновления.
Рассмотрим два источника:
- Учебник по обновлению DRAM от Университета штата Юта
- И отличная документация гигабитного чипа от Micron: «Проектирование TN-46-09 для 1Gb DDR SDRAM»
Каждый бит в динамической памяти должен обновляться: обычно это происходит каждые 64 мс (так называемое статическое обновление). Это довольно дорогостоящая операция. Чтобы избежать одной крупной остановки каждые 64 мс, процесс разделён на 8192 меньшие операции обновления. В каждой из них контроллер памяти компьютера отправляет команды обновления на микросхемы DRAM. После получения инструкции чип обновит 1/8192 ячеек. Если посчитать, то 64 мс / 8192 = 7812,5 нс или 7,81 мкс. Это значит следующее:
- Команда обновления выполняется каждые 7812,5 нс. Она называется tREFI.
- Процесс обновления и восстановления занимает некоторое время, поэтому чип может снова выполнять обычные операции чтения и записи. Так называемое tRFC равняется или 75 нс, или 120 нс (как в упомянутой документации Micron).
Если память горячая (более 85°C), то время хранения данных в памяти падает, а время статического обновления снижается вдвое до 32 мс. Соответственно, tREFI падает до 3906,25 нс.
Типичная микросхема памяти занята обновлениями в течение значительной части времени своей работы: от 0,4% до 5%. Кроме того, чипы памяти отвечают за нетривиальную долю энергопотребления типичного компьютера, и большая часть этой мощности тратится на выполнение обновлений.
На время обновления блокируется вся микросхема памяти. То есть каждый бит в памяти заблокирован в течениее более 75 нс каждые 7812 нс. Давайте измерим.
Подготовка эксперимента
Чтобы измерить операции с наносекундной точностью, нужен очень плотный цикл, возможно, на C. Он выглядит так:
for (i = 0; i < ...; i++) {
// Загрузка в память.
*(volatile int *) one_global_var;
// Очистка кэша CPU. Она относительно медленная
_mm_clflush(one_global_var);
// нужен барьер памяти, иначе иногда цикл может
// пройти очень быстро (25 нс вместо примерно 160).
// Думаю, из-за переупорядочивания.
asm volatile("mfence");
// Измерение и запись времени
clock_gettime(CLOCK_MONOTONIC, &ts);
}Полный код доступен на GitHub.
Код очень простой. Выполняем чтение памяти. Сбрасываем данные из кэша CPU. Измеряем время.
(Примечание: во втором эксперименте я попытался для загрузки данных использовать MOVNTDQA, но это требует специальной некэшируемой страницы памяти и рутовых прав).
На моём компьютере программа выдаёт такие данные:
# метка времени, длительность цикла 3101895733, 134 3101895865, 132 3101896002, 137 3101896134, 132 3101896268, 134 3101896403, 135 3101896762, 359 3101896901, 139 3101897038, 137
Обычно получается цикл длительностью около 140 нс, периодически время подскакивает до примерно 360 нс. Иногда выскакивают странные результаты больше 3200 нс.
К сожалению, данные получаются слишком шумными. Очень трудно увидеть, есть ли заметная задержка, связанная с циклами обновления.
Быстрое преобразование Фурье
В какой-то момент меня осенило. Поскольку мы хотим найти событие с фиксированным интервалом, можно подать данные в алгоритм FFT (быстрое преобразование Фурье), который расшифрует основные частоты.
Я не первый, кто подумал об этом: Марк Сиборн со знаменитой уязвимостью Rowhammer реализовал эту самую технику ещё в 2015 году. Даже посмотрев код Марка, заставить FFT работать оказалось сложнее, чем я ожидал. Но в конце концов я собрал все кусочки воедино.
Сначала нужно подготовить данные. FFT требует входных данных с постоянным интервалом выборки. Мы также хотим обрезать данные, чтобы уменьшить шум. Методом проб и ошибок я обнаружил, что лучший результат достигается после предварительной обработки данных:
- Малые значения (меньше, чем 1,8 среднего) итераций цикла отрезаются, игнорируются и заменяются нулями. Мы действительно не хотим вводить шум.
- Все остальные показания заменяются единицами, так как нам действительно не важна амплитуда задержки, вызванной некоторым шумом.
- Я остановился на интервале выборки 100 нс, но подойдёт любое число до частоты Найквиста (двойная ожидаемая частота).
- Данные должны быть отобраны с фиксированным временем перед подачей в БПФ. Все разумные методы выборки работают нормально, я остановился на базовой линейной интерполяции.
Алгоритм примерно такой:
UNIT=100ns
A = [(timestamp, loop_duration),...]
p = 1
for curr_ts in frange(fist_ts, last_ts, UNIT):
while not(A[p-1].timestamp <= curr_ts < A[p].timestamp):
p += 1
v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0
v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0
v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp)
B.append( v )Который на моих данных производит довольно скучный вектор типа такого:
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...]
Впрочем, вектор довольно большой, обычно около 200 тыс. точек данных. С такими данными можно использовать FFT!
C = numpy.fft.fft(B)
C = numpy.abs(C)
F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)Довольно просто, правда? Это производит два вектора:
- C содержит комплексные числа частотных компонентов. Нас не интересуют комплексные числа, и можно сгладить их командой
abs(). - F содержит метки, какой частотный промежуток лежит в каком месте вектора C. Нормализуем показатель до герц умножением на частоту дискретизации входного вектора.
Результат можно нанести на диаграмму:
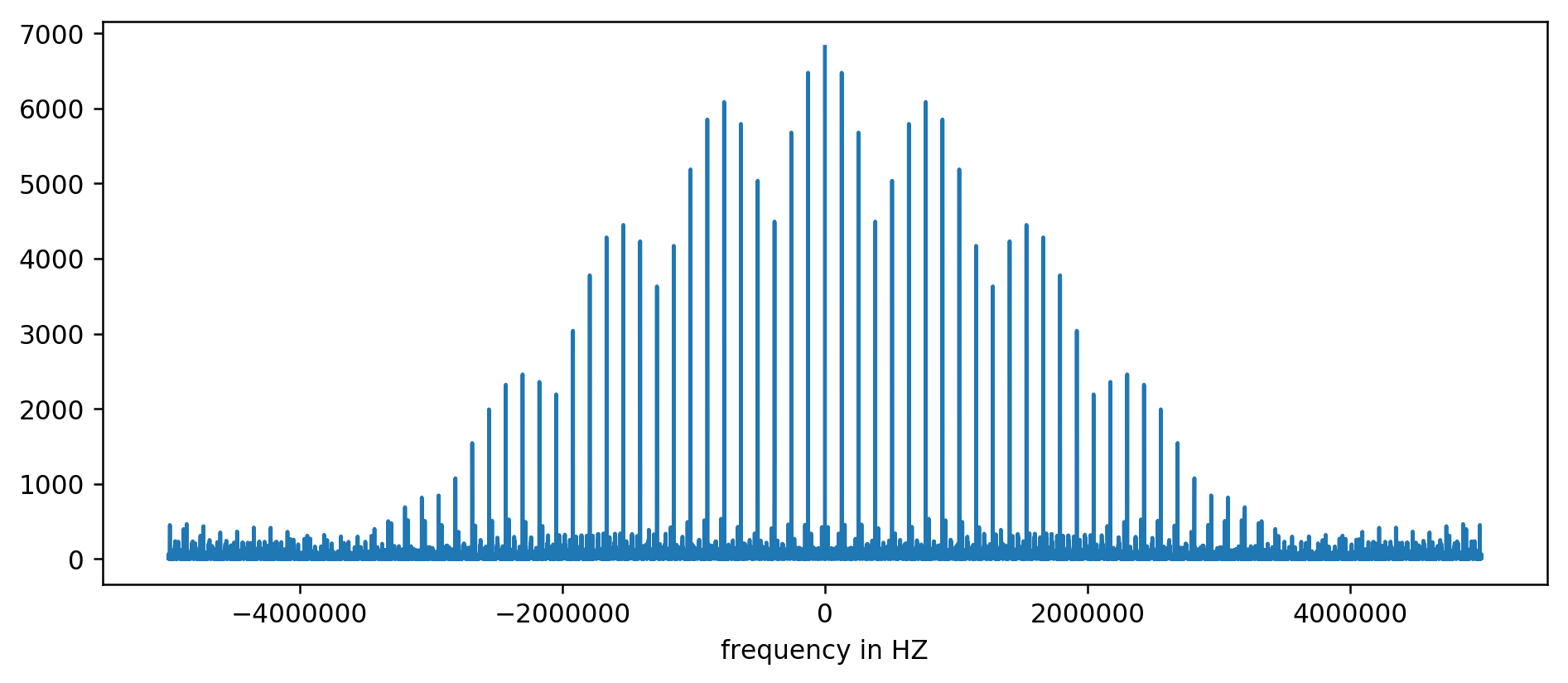
Ось Y без единиц измерения, поскольку мы нормализовали время задержки. Несмотря на это, чётко видны всплески в некоторых фиксированных интервалах частот. Рассмотрим их ближе:
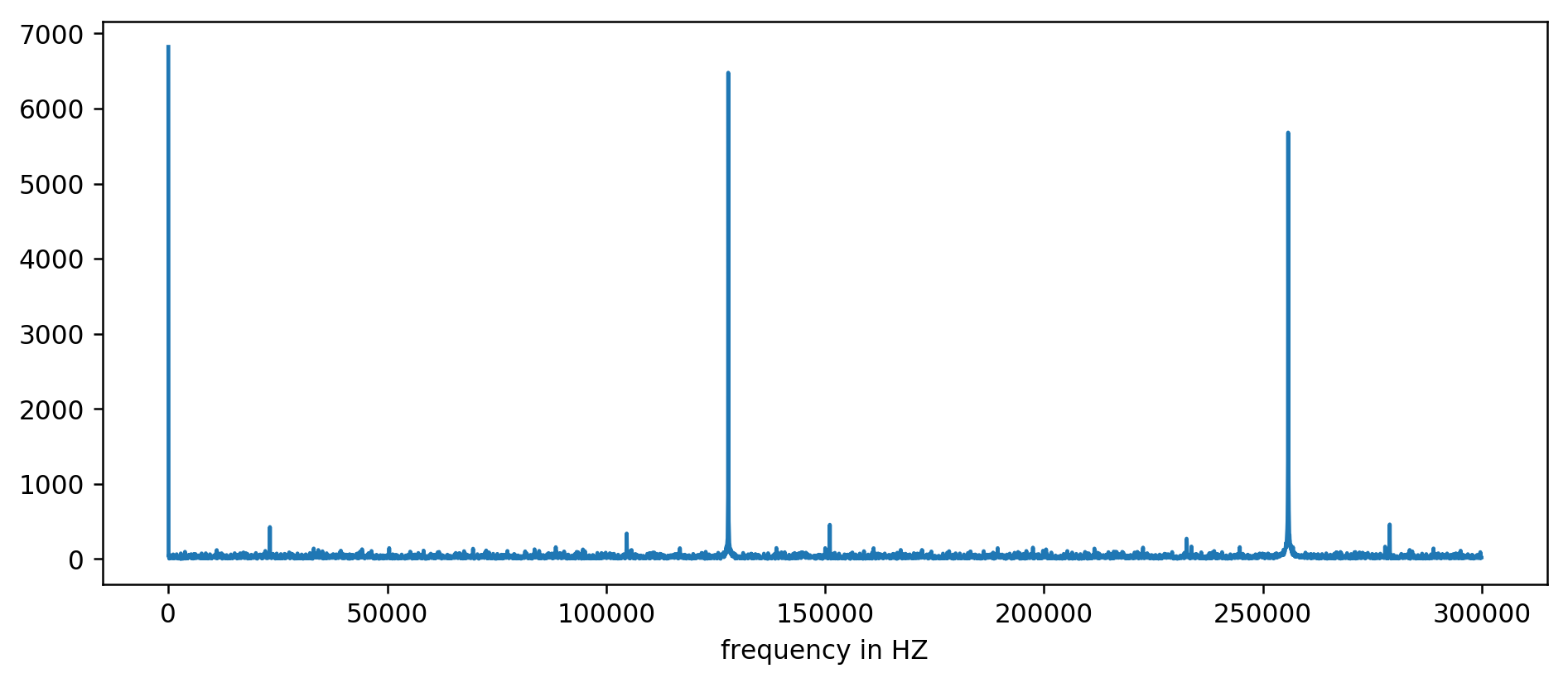
Мы ясно видим три первых пика. После немного невыразительный арифметики, включая фильтрацию чтения как минимум в десятикратном размере среднего, можно извлечь базовые частоты:
127850.0 127900.0 127950.0 255700.0 255750.0 255800.0 255850.0 255900.0 255950.0 383600.0 383650.0
Считаем: 1000000000 (нс/с) / 127900 (Гц) = 7818,6 нс
Ура! Первый скачок частоты — это действительно то, что мы искали, и он действительно коррелирует со временем обновления.
Остальные пики на 256 кГц, 384 кГц, 512 кГц — это так называемые гармоники, кратные нашей базовой частоте 128 кГц. Это полностью ожидаемый побочный эффект применения FFT на чём-то вроде прямоугольной волны.
Для облегчения экспериментов мы сделали версию для командной строки. Можете самостоятельно запустить код. Вот пример запуска на моём сервере:
~/2018-11-memory-refresh$ make gcc -msse4.1 -ggdb -O3 -Wall -Wextra measure-dram.c -o measure-dram ./measure-dram | python3 ./analyze-dram.py [*] Verifying ASLR: main=0x555555554890 stack=0x7fffffefe2ec [ ] Fun fact. I did 40663553 clock_gettime()'s per second [*] Measuring MOVQ + CLFLUSH time. Running 131072 iterations. [*] Writing out data [*] Input data: min=117 avg=176 med=167 max=8172 items=131072 [*] Cutoff range 212-inf [ ] 127849 items below cutoff, 0 items above cutoff, 3223 items non-zero [*] Running FFT [*] Top frequency above 2kHz below 250kHz has magnitude of 7716 [+] Top frequency spikes above 2kHZ are at: 127906Hz 7716 255813Hz 7947 383720Hz 7460 511626Hz 7141
Должен признать, код не совсем стабилен. В случае проблем рекомендуется отключить Turbo Boost, масштабирование частоты CPU и оптимизацию для производительности.
Заключение
Из этой работы есть два основных вывода.
Мы увидели, что данные низкого уровня довольно трудно анализировать и они кажутся довольно шумными. Вместо оценки невооружённым глазом всегда можно использовать старый добрый БПФ. При подготовке данных необходимо в каком-то смысле принять желаемое за действительное.
Самое главное, мы показали, что зачастую возможно измерить тонкое аппаратное поведение из простого процесса в пользовательском пространстве. Такого рода мышление привело к открытию оригинальной уязвимости Rowhammer, оно реализовано в атаках Meltdown/Spectre и снова показано в недавней реинкарнации Rowhammer для памяти ECC.
Многое осталось за рамками данной статьи. Мы едва коснулись внутренней работы подсистемы памяти. Для дальнейшего чтения рекомендую:
- Отображение кэша L3 на процессорах Sandy Bridge
- Как физический адрес сопоставляется со строками и банками в DRAM
- Ханну Хартикайнен взломал DDR3 SO-DIMM и заставил его работать… медленнее
Наконец, вот хорошее описание старой ферритовой памяти:
Комментарии (54)

pfemidi
25.11.2018 22:13+1Перевод сделал мне день ;-)
Оригинал:
// Perform memory load. Any will do
*(volatile int *) one_global_var;
Перевод:
// Загрузка памяти. Любая инструкция загрузки делает
*(volatile int *) one_global_var;

hdfan2
26.11.2018 07:54Туда же: «нетривиальную долю энергопотребления» -> «значительную/существенную долю энергопотребления».

Mad__Max
26.11.2018 10:38И сверху: «Процесс обновления и восстановления занимает некоторое время, поэтому чип может снова выполнять обычные операции чтения и записи» ==> «Процесс обновления и восстановления занимает некоторое время, прежде чем чип сможет снова выполнять обычные операции чтения и записи».
Вроде мелочи, но смысл практически на противоположный меняется — можно подумать, что чип нормально продолжает заниматься обычной работой параллельно с обновлением данных в ячейках. А на самом деле нет, не может — все курят бамбук, до тех пор пока он не закончит обновление. Собственно поэтому и задержки, если бы это шло в фоновом режиме, никаких задержек просто не было.

Refridgerator
26.11.2018 06:20+1C содержит комплексные числа частотных компонентов. Нас не интересуют комплексные числа, и можно сгладить их командой abs()
Функция abs() не «сглаживает» комплексные числа, а извлекает модуль (амплитуду).

postgres
26.11.2018 08:42В программах Aida и подобных ей замечал характеристику памяти:
«Частота регенерации памяти = 7.8 µs”
Mad__Max
26.11.2018 10:33tRFC (сколько занимает это самое обновление) в расширенных таймингах памяти так же указывается (и пишется в спомогательный чип на модуле памяти — SPD).
Только не в наносекундах, а в тактах привязанных к частоте работы самой памяти. Например сейчас с которого пишу:
9-9-9-27 (CL-RCD-RP-RAS) / 36-128-0-5-12-6-6-24 (RC-RFC-CR-RRD-WR-WTR-RTP-FAW)
RFC=128 тактов
рабочая частота 1600 МГц
1/1600000000*128=80 нс
По столько память тупит («уходит в себя») при каждом обновлении, трогать ее в этот момент не моги (с).

maydjin
26.11.2018 09:42Информация интересная, спасибо.
Хинт — большинство попсовых компиляторов поддерживают интристик __rdtsc();
P.S. А affinity вы же выставляли в ваших экспериментах? А то весь этот "шум" как и наблюдаемые данные, могли оказаться переключениями контекста. Ну а как известно, кто ищет — тот всегда найдёт...

vesper-bot
26.11.2018 17:03По идее, события переключения контекста должны давать гармонику на FFT, но они малость менее часты, 20мс ЕМНИП квант времени, а измеряются задержки куда более низкого порядка. В его 200к векторе событий переключения контекста ожидается одно (2e5*1e-7/2e-2 = 1), т.е. на FFT просто не попадет.

maydjin
26.11.2018 17:57Да, об этом я не подумал. Там же нет блокирующих вызовов, по идее такой пик если и попадёт то будет далеко выпадать на фоне остальных замеров.

Mad__Max
27.11.2018 03:1115-20мс для фоновых процессов или на серверных системах. Если запущенно что-нибудь интерактивное (хоть браузер или там медиаплеер), то обычно квантование мельчится вплоть до 1 мс (на новых ОС может и еще мельче), чтобы пользователь не замечал микролагов и рывков(если например видео смотрит или в игрушку играет) при переключениях.

vesper-bot
27.11.2018 09:24Хм, спасибо за информацию. Все равно слишком далеко от найденной частоты. :)

SomaTayron
26.11.2018 11:53С ферромагнетиками для кодирования памяти проблем в общем то не много, и были попытки не только с одиночными кольцами (кольцо — исключительно чтоб не фонило). Поясню на феррозондах (не по 2 гармонике, о просто по петле) — как-никак диссер по этому был )))
Имеем 2 параллельных сердечника с последовательно-встречно намотанными катушками, один из которых с условным пермаллоем, второй — с воздушным сердечником (к примеру пластик). Если есть сильное внешнее поле, то пермаллой насыщается. Тогда, если в катушки дать прямоугольный импульс, то на измерительной (охватывает оба сердечника) катушке суммарное поле будет нулевым. А вот если внешнее поле слабое, то катушка с пермаллоем будет преобладать и мы регистрируем единичку. В таком варианте чтение ничего не стирает и управление записью и чтением разделено.
Плохо, что такие решения были громоздкими, потому и не пережили конкуренции

DrunkBear
26.11.2018 11:57Хорошо, память обновляется, нагретая — обновляется чаще.
Это как-то влияет на производительность? Или можно пренебречь? Может, лучше греть память и получать рекорды, вместо глубокой заморозки азотом?
И как заморозка влияет на частоту и время обновления?
Fly3110
26.11.2018 12:33+1Естественно влияет. В моменты обновления память недоступна.
Больше температура, больше моментов обновления => память чаще недоступна.
Так что надо охлаждать, чтобы не перегревалась
Mad__Max
27.11.2018 03:19С учетом где проходит граница (85 гр), охлаждать на практике не нужно. Само она до такой температуры не нагреется, даже в «голом»(только платка модуля с чипами) виде.
Разве что в какой-нибудь промышленной железяке, где она не сама греется, а от внешних источников тепла может сильно нагреваться.

jok40
26.11.2018 12:40Насколько мне известно, в компьютерах нет динамического изменения частоты регенерации оперативки в зависимости от температуры. Контроллер памяти настраивается один раз при включении и не меняет тайминги при дальнейшей работе.

Rohan66
26.11.2018 13:56В училище изучал работу такой памяти…
В нашей машине ППЗУ было такое. На биаксах построено. Машина 5Э26.

catharsis
26.11.2018 14:21Теперь нужно нагреть память и обнаружить новую нулевую гармонику.
Гипертрединг наверное тоже лучше выключить.
А вот как отфильтровать переключения контекста у меня пока идей нет. По идее переключение туда-обратно должно занимать хотя бы 1 мкс, но было бы круто это проверить.
SergeyMax
26.11.2018 17:42Перекомпилить приложение и померять под DOS с заблокированными прерываниями.

Elmot
26.11.2018 16:10+1По-моему не статья, а чушь какая-то.
В современном CPU несколько ядер + гипертрейдинг. По пути от CPU до памяти конвейер 2 или 3 шины, спекулятивное исполнение и 3 уровня кэша. Параллельно происходят прерывания, DMA доступ, в ряде случаев(интегрированная графика) графический чип лезет в ту же память за своими данными. Битность шины памяти никак не учитывается, количество каналов тоже, и, как мне кажется, современные модули DRAM обновляют память прозрачно для шин памяти. Автор скорее всего поймал частоту какого-нибудь системного таймера, тяжело и долго переключающего процессы и контексты, а вовсе не memory refresh.

mpa4b
26.11.2018 17:38+1Следует понимать причину того, что в статье 'виден' период обновления.
1. Память разделена на 'ряды' (rows) (и 'банки', но это не так важно). При первом чтении из ряда, он 'открывается' и остаётся открытым. Последующие чтения идут уже из открытого ряда и следовательно они быстрее.
2. При рефреше открытый ряд (каким бы он ни был) закрывается и выдаётся команда рефреша. При последующем обращении к тому же ряду он снова открывается.
Таким образом, в статье виден именно процесс торможения при открытии ряда, вызванный в том числе и рефрешем. Если последовательно читать из разных рядов (в пределах одного банка), то такое 'торможение' будет происходить при каждом чтении (т.к. в одном банке открыт может быть только 1 ряд)

vagon333
26.11.2018 19:33Если только не в бешенной спешке, всегда заезжаю в этот музей. Вдохновляет. Рекомендую.

thealfest
27.11.2018 07:43Во времена доса были программы, ускоряющие компьютер путем замедления регенерации памяти (путем программирования одного из каналов таймера).


ky0
Это очень крутая опечатка :) Единица лагания — один Микрософт.
m1rko Автор
Это не опечатка, настроил автозамену на свою голову… Извините! :)
tvr
Даже и не думайте извиняться. это так хорошо лагло в тему. :)
NetBUG
Лагло, но не очень хорошее, всего 10% времени лагает. Хорошее лагло лагает 100% времени!
Mad__Max
Не, если 100% это все-таки не лагло, это уже висяк.
Jeyko
Это надо обязательно ввести в оборот! Срочно в палату мер!: )
opckSheff
Что же вы советуете? Мировая наука старается уйти от привязки единиц измерения к физическим эталонам, а вы тут майкрософт в палату мер и весов тащите…
TheShock
Ну ее можно описать через что-то физическое. Типа «1 микрософт равен количеству мата, которое хочется сказать за 16732415351 периодами излучения атома стронция при использовании их продуктов». Хотя и этого недостаточно. Стронций ведь непостоянное излучение имеет, да?
JekaMas
Нужен фундаментальный закон, из которого 1 MS выводится однозначно.
Уверен, что оно существует.
8street
Микрософт довольно маленькая величина. Миллисофт побольше, а Софт уже очень большая. Также есть Пикософт и Фемтософт, но их зафиксировать трудно.
JekaMas
Да, только при слиянии сверхмассивных черных дыр, поглотивших не менее миллионов солнц денег...
Barafu_Albino_Cheetah
Ну можно взять, что 1 софт = максимально возможная бажность, когда по ошибке в каждой идиоме кода. Тогда один микрософт — по 1 ошибке в каждой 1000 идиом, что вообще похоже на правду.
mk2
Это по 1 ошибке в 1000000 идиом, а у вас миллисофт.
TheShock
Может тогда не «идиом», а «атомарных операций»?
1 микрософт — это 1 ошибка на 1000000 атомарных операций.
hdfan2
Количество мата, производимое шарообразным абсолютно упругим абсолютно чёрным пользователем ПО Microsoft, диаметром в один метр и весом в один килограмм за одну секунду. В вакууме, разумеется.
cyberly
Это уже какой-то эталон из области политкорректности.
KodyWiremane
Мне кажется, для вакуума лучше сказать «количество излучённой энергии», а матерность выразить через спектр излучения.
И ПО надо какое-то явно определить эталонное. Либо через объём кода, мб энтропию…
amarao
Очевидно, что нужно мерять звуковую энергию. Дополнительный объём энергии, который рассеивает через мат абсолютно чёрный сферический пользователь после принудительного апдейта на W10.
KodyWiremane
Звуковую? В вакууме?
amarao
Да. Мат материален (по произношению), а значит, в нём могут быть звуковые волны. Более того, мат — звук, а значит волна.
Вот так вот и проявляется корпускулярно-волновой дуализм мата.
KodyWiremane
Чтобы измерить звуковую волну, нужно, чтобы она дошла до измерителя, а в вакууме мне это видится проблематичным, т. к. звук является колебательным процессом в веществе, а вакуум есть отсутствие вещества. По мне, мерять тепло надёжней.
amarao
Как только до наблюдателя дойдёт излучаемый мат, то он его сможет измерить.
PS
Тепло — энергия, энергия — масса, масса — наличие вещества.
KodyWiremane
Удачи в экспериментах :)
Vlad5
Давайте вернём среднее арифметическое длины ступни 12 взрослых людей — фут, ну или дюймы. Только потом не стоните, что поршня на вашем «Порше» не лезут в блок или наоборот, пролетают со свистом. В технике от эталона не уйти, и, если не ошибаюсь, даже в странах с англицкой системой мер и весов рекомендуют переходить на метрическую.
TheShock
Вы не поняли комментарий, на который так критически ответили.
cyberly
Да ну, миллион весьма высокоточных вещей имеет дюймовые размеры. Почему вы думаете калибр АК47 такой некруглый? А «в странах с англицкой системой мер и весов», вроде как, когда очень нужно, как и с миллиметрами, просто используют точно такие же десятичные дроби с нужным числом знаков после запятой.
Vlad5
Проблема только в том, что метр, он и в Африке метр, а вот дюймов примерно под 30 видов/размеров, футов вообще более 60. И получается в итоге, что в дюймах, что в попугаях.