Уже довольно долго использую QML для построения графических интерфейсов, но возможности поработать в реальном проекте с Qt Location API и QML Map, до настоящего времени, не было.
Поэтому стало интересно попробовать эту компоненту для построения воздушных трасс.
Под катом описание реализации редактора, для создания подобных траекторий на карте:

Для упрощения реализации, наши самолеты летают в 2D плоскости на одной высоте. Скорость и допустимая перегрузка зафиксированны — 920 км/ч и 3g, что дает радиус поворота
Траектория состоит из сегментов следующего вида:

где S — начало маневра (она же точка выхода из предыдущего), M — начало поворота, E — выход из него, а F — финальная точка (М для следующего).
Для просчета точки входа и выхода из траектории использовал уравнение касательной к окружности, выкладки получились довольно громоздкими, уверен, можно сделать проще.
Завершив просчет математической модели нашей траектории, приступим к работе непосредственно с картой. Естественный выбор для построения ломаных линий на QML карте это добавление MapPolyline непосредственно на карту.
Изначально мне хотелось предоставить пользователю возможность моделировать каждый следующий участок маршрута «на лету» — создать ефект движения траектории за курсором.
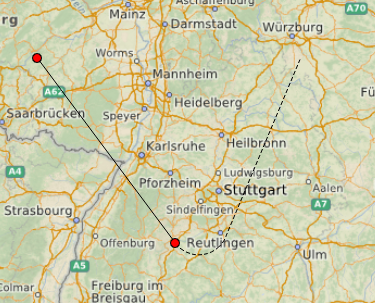
Изменение path при движение курсора, является довольно затратной операцией, поэтому я попробовал использовать предварительные «пиксельные» траектории, которые отображаются до того момента, как юзер окончательно сохранит маршрут.
FlightItem является QQuickItem-ом, а QAbstractListModel flightModel позволяет обновлять необходимые участки траектории при изменение данных для маневра.
Такой лайв-апдейт позволяет предупреждать пользователя о нереализуемых маневрах.
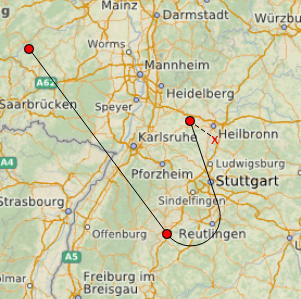
Только после завершения создания воздушной трассы (например при right mouse click) трасса окончательно будет добавлена на QML Map как GeoPath с возможностью геопривязки (до этого момента двигать и зумить карту нельзя, пиксели ничего не знают о долготе и широте).
Для того чтобы пересчитать пиксельный сегмент в геокоординатный нам для начала нужно для каждого маневра использовать локальную относительно точки входа в маневр (наша точка S) систему координат.
После того как мы пересчитаем маневр уже метрах необходимо проделать обратную операцию и зная геопривязку точки S перевести метры в широту-долготу.
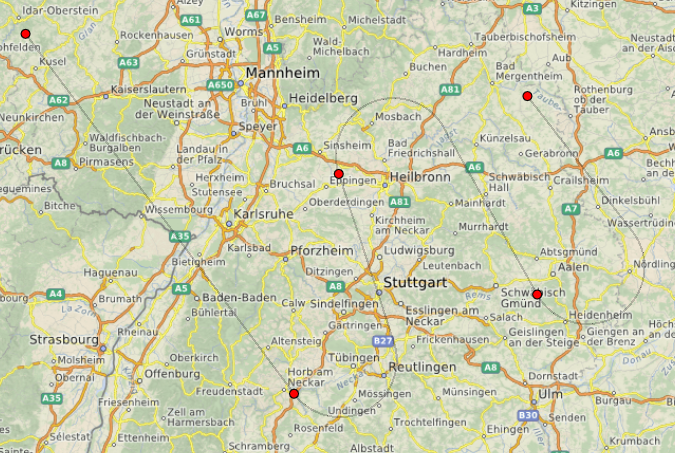
С формальной точки зрения нельзя, конечно, считать нашу «пиксельную» и «в метрах» траекторию идентичной, но очень уж вкусной мне показалась возможность заглянуть в будущее и показать пользователю, что будет (или не будет, если самолет так не летает), когда он кликнет в следующий раз. После финализации траектории (она немного отличается от пиксельной по цвету и прозрачности, так как даже статические ломаные линии не очень гладко выглядат на карте).
Исходники доступны тут, для компиляции использовал Qt 5.11.2.
В следующей части, мы научим наш редактор двигать опорные точки траектории, а также сохранять/открывать существующие трассы для последующей имитации движения самолетов.
Поэтому стало интересно попробовать эту компоненту для построения воздушных трасс.
Под катом описание реализации редактора, для создания подобных траекторий на карте:

Для упрощения реализации, наши самолеты летают в 2D плоскости на одной высоте. Скорость и допустимая перегрузка зафиксированны — 920 км/ч и 3g, что дает радиус поворота
Траектория состоит из сегментов следующего вида:

где S — начало маневра (она же точка выхода из предыдущего), M — начало поворота, E — выход из него, а F — финальная точка (М для следующего).
Для просчета точки входа и выхода из траектории использовал уравнение касательной к окружности, выкладки получились довольно громоздкими, уверен, можно сделать проще.
void Manoeuvre::calculate()
{
// General equation of line between first and middle points
auto A = mStart.y() - mMiddle.y();
auto B = mMiddle.x() - mStart.x();
// Check cross product sign whether final point lies on left side
auto crossProduct = (B*(mFinal.y() - mStart.y()) + A*(mFinal.x() - mStart.x()));
// All three points lie on the same line
if (isEqualToZero(crossProduct)) {
mIsValid = true;
mCircle = mExit = mMiddle;
return;
}
mIsLeftTurn = crossProduct > 0;
auto lineNorm = A*A + B*B;
auto exitSign = mIsLeftTurn ? 1 : -1;
auto projection = exitSign*mRadius * qSqrt(lineNorm);
// Center lies on perpendicular to middle point
if (!isEqualToZero(A) && !isEqualToZero(B)) {
auto C = -B*mStart.y() - A*mStart.x();
auto right = (projection - C)/A - (mMiddle.x()*lineNorm + A*C) / (B*B);
mCircle.ry() = right / (A/B + B/A);
mCircle.rx() = (projection - B*mCircle.y() - C) / A;
} else {
// Entering line is perpendicular to either x- or y-axis
auto deltaY = isEqualToZero(A) ? 0 : exitSign*mRadius;
auto deltaX = isEqualToZero(B) ? 0 : exitSign*mRadius;
mCircle.ry() = mMiddle.y() + deltaY;
mCircle.rx() = mMiddle.x() + deltaX;
}
// Check if final point is outside manouevre circle
auto circleDiffX = mFinal.x() - mCircle.x();
auto circleDiffY = mFinal.y() - mCircle.y();
auto distance = qSqrt(circleDiffX*circleDiffX + circleDiffY*circleDiffY);
mIsValid = distance > mRadius;
// Does not make sence to calculate futher
if (!mIsValid)
return;
// Length of hypotenuse from final point to exit point
auto beta = qAtan2(mCircle.y() - mFinal.y(), mCircle.x() - mFinal.x());
auto alpha = qAsin(mRadius / distance);
auto length = qSqrt(distance*distance - mRadius*mRadius);
// Depends on position of final point find exit point
mExit.rx() = mFinal.x() + length*qCos(beta + exitSign*alpha);
mExit.ry() = mFinal.y() + length*qSin(beta + exitSign*alpha);
// Finally calculate start/span angles
auto startAngle = qAtan2(mCircle.y() - mMiddle.y(), mMiddle.x() - mCircle.x());
auto endAngle = qAtan2(mCircle.y() - mExit.y(), mExit.x() - mCircle.x());
mStartAngle = startAngle < 0 ? startAngle + 2*M_PI : startAngle;
endAngle = endAngle < 0 ? endAngle + 2*M_PI : endAngle;
auto smallSpan = qFabs(endAngle - mStartAngle);
auto bigSpan = 2*M_PI - qFabs(mStartAngle - endAngle);
bool isZeroCrossed = mStartAngle > endAngle;
if (!mIsLeftTurn) {
mSpanAngle = isZeroCrossed ? bigSpan : smallSpan;
} else {
mSpanAngle = isZeroCrossed ? smallSpan : bigSpan;
}
}
Завершив просчет математической модели нашей траектории, приступим к работе непосредственно с картой. Естественный выбор для построения ломаных линий на QML карте это добавление MapPolyline непосредственно на карту.
Map {
id: map
plugin: Plugin { name: "osm" }
MapPolyline {
path: [ { latitude: -27, longitude: 153.0 }, ... ]
}
}Изначально мне хотелось предоставить пользователю возможность моделировать каждый следующий участок маршрута «на лету» — создать ефект движения траектории за курсором.

Изменение path при движение курсора, является довольно затратной операцией, поэтому я попробовал использовать предварительные «пиксельные» траектории, которые отображаются до того момента, как юзер окончательно сохранит маршрут.
Repeater {
id: trajectoryView
model: flightRegistry.hasActiveFlight ?
flightRegistry.flightModel : []
FlightItem {
anchors.fill: parent
startPoint: start
endPoint: end
manoeuvreRect: rect
manoeuvreStartAngle: startAngle
manoeuvreSpanAngle: spanAngle
isVirtualLink: isVirtual
}
}FlightItem является QQuickItem-ом, а QAbstractListModel flightModel позволяет обновлять необходимые участки траектории при изменение данных для маневра.
QVariant FlightModel::data(const QModelIndex &index, int role) const
{
if (!index.isValid()) {
return QVariant();
}
switch (role) {
case FlightRoles::StartPoint:
return mFlight->flightSegment(index.row()).line().p1();
case FlightRoles::EndPoint:
return mFlight->flightSegment(index.row()).line().p2();
...
}
Такой лайв-апдейт позволяет предупреждать пользователя о нереализуемых маневрах.

Только после завершения создания воздушной трассы (например при right mouse click) трасса окончательно будет добавлена на QML Map как GeoPath с возможностью геопривязки (до этого момента двигать и зумить карту нельзя, пиксели ничего не знают о долготе и широте).
Для того чтобы пересчитать пиксельный сегмент в геокоординатный нам для начала нужно для каждого маневра использовать локальную относительно точки входа в маневр (наша точка S) систему координат.
QPointF FlightGeoRoute::toPlaneCoordinate(const QGeoCoordinate &origin,
const QGeoCoordinate &point)
{
auto distance = origin.distanceTo(point);
auto azimuth = origin.azimuthTo(point);
auto x = qSin(qDegreesToRadians(azimuth)) * distance;
auto y = qCos(qDegreesToRadians(azimuth)) * distance;
return QPointF(x, y);
}После того как мы пересчитаем маневр уже метрах необходимо проделать обратную операцию и зная геопривязку точки S перевести метры в широту-долготу.
QGeoCoordinate FlightGeoRoute::toGeoCoordinate(const QGeoCoordinate &origin, const QPointF &point)
{
auto distance = qSqrt(point.x()*point.x() + point.y()*point.y());
auto radianAngle = qAtan2(point.x(), point.y());
auto azimuth = qRadiansToDegrees(radianAngle < 0 ? radianAngle + 2*M_PI
: radianAngle);
return origin.atDistanceAndAzimuth(distance, azimuth);
}С формальной точки зрения нельзя, конечно, считать нашу «пиксельную» и «в метрах» траекторию идентичной, но очень уж вкусной мне показалась возможность заглянуть в будущее и показать пользователю, что будет (или не будет, если самолет так не летает), когда он кликнет в следующий раз. После финализации траектории (она немного отличается от пиксельной по цвету и прозрачности, так как даже статические ломаные линии не очень гладко выглядат на карте).

Исходники доступны тут, для компиляции использовал Qt 5.11.2.
В следующей части, мы научим наш редактор двигать опорные точки траектории, а также сохранять/открывать существующие трассы для последующей имитации движения самолетов.
Комментарии (9)

OldGrumbler
23.12.2018 00:53-1создать ефект движения
Мне одному кажется, что автор текста за одно это слово обязан пройти полный курс Живительной Эвтаназии? )))
На самом деле, грош цена всем вышеописанным расчетам без учета особенностей аэродромов в точках маршрутов. Как и без учета конкретных, ежечасно минимум меняющихся метеоусловий.
Потому что при перемене ветра самолет запросто может перекатиться в другую сторону полосы и поменять взлетный курс на 180 градусов — иначе он спалит в разы больше топлива, чем даст ему «оптимизация по глобусу».
Учить матчасть, выкидывать комп и осваивать НЛ-10, а потом приходить в этот тред чисто на поржать.
)))

roach1967
23.12.2018 12:07Мне кажется, что логичнее ставить реперную точку не на начало манёвра, а на середину. Или даже дать возможность менять положение на дуге манёвра. Тогда и запрещённые моменты практически исчезнут (как на предпоследней карте).



bogolt
Из-за повсеместного auto читать код очень трудно. Например я смотрю на
mRadius / distanceи думаю а вдруг оба значения целочисленные? Смотрю на distance а он auto — значит надо смотреть на породившее его выражение. А если оно тоже из переменных которые auto?etho0
Зачем вам знать целочисленное ли это значение?
bogolt
потому что
int a,b;
a/b
float a,b;
a/b;
дадут совершенно разные результаты. И мне глядя на код неясно не случится ли там подобная беда с отбрасываем дробной части.
Sazonov
Именно поэтому в cpp core guidelines для мер использовать специальные типы данных. Тогда не будет никакой путаницы с корректностью рассчётов даже при повсеместном auto