В онлайн-контесте приняло участие 1199 человек, а решений набралось больше 5000, среди которых 61 решение — попытки обойти систему с помощью нахождения уязвимостей. Это очень круто, спасибо всем, кто принял участие.
Эта игра представляет собой тип “игр полковника Блотто”. В ней принимают участие два игрока. У каждого одинаковое кол-во ресурсов, которое нужно разместить на поле NxM. Побеждает тот, кто займет больше клеток (т.е. кол-во ваших ресурсов на ней больше, чем у оппонента). Так выглядит условие для нашей задачи
2. Поле игры представляет собой доску размера 3 на 3.
3. Каждый игрок располагает армией в 100 космодесантников.
4. Перед битвой ночью каждая сторона втайне размещает свои отряды произвольным способом на 9-и клетках. На каждую клетку можно поставить любое целое число космодесантников от 0 до 100.
5. Утром начинается сражение за очередную планету. На каждой из 9 клеток побеждает тот игрок, у кого на этой клетке стоит больше астартес. За победу на каждой из 9 клеток дается 1 очко. Если на некоторой клетке стоит одинаковое число, то сражение на этой клетке заканчивается вничью, и оба игрока получают 0,5 очка.
6. Сражение выигрывает тот, кто выиграл больше полей. Если оба игрока выиграли по 4,5 поля, сражение заканчивается вничью.
Когда я запустил этот эксперимент, я еще не знал, что у этой игры нет идеального решения, но благодаря комментариям я смог лучше разобраться в этой теме.
Начнем с победителей этой игры
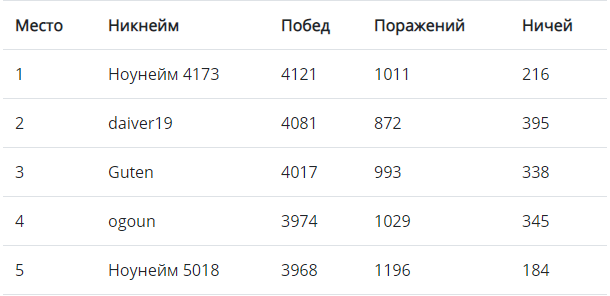

Лучшее решение набрало 4121 побед — весьма неплохой результат. Но что было бы, если бы в игре участвовали решения только из ТОП-100?
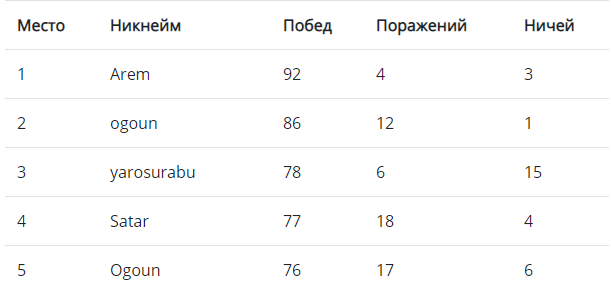
Удивительно, но оно не вошло даже в топ5 (на 8м месте), а 1е место здесь заняло решение с 68-го места.

Это как раз показывает, что лучшего решения нет. Остальные результаты можно посмотреть на game.pavlukhinlab.com
Но что еще интересного можно узнать?
Самые большие числа игроки ставили в центр, в среднем все игроки заполняли первую строку большими числами, в то время как лучшие результаты делали больший упор на нижнюю строку.


средние значения по всем играм (слева) и по ТОП-100 (справа)
Ну и еще примеры лучших стратегий:




Лучшие стратегии выбирали 5 основных клеток, оставшиеся клетки заполнялись мелкими значениями. Что логично, ведь для победы достаточно занять 5 клеток.
Ну а теперь немного графиков.
Вероятностные распределения чисел:
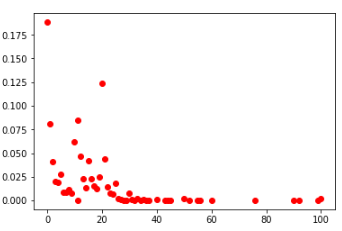
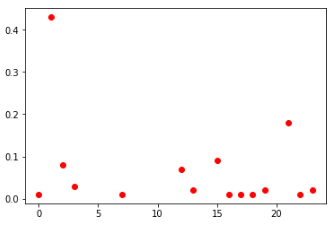
вторые клетки среди всех игроков (слева) и ТОП-100 (справа)
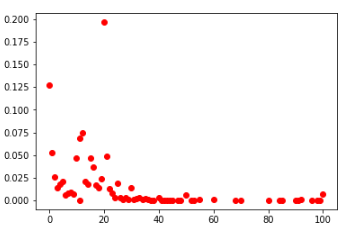
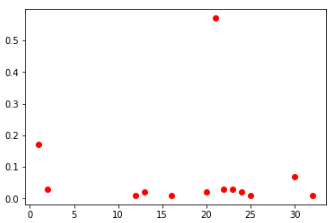
центральные клетки среди всех и ТОП-100
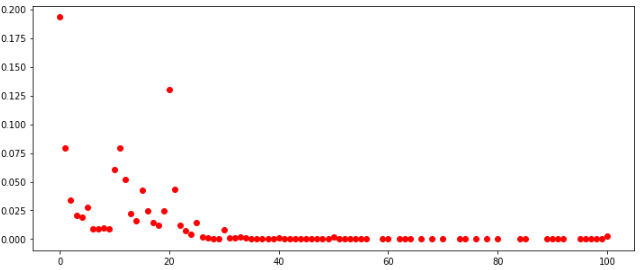
распределение чисел по всем играм
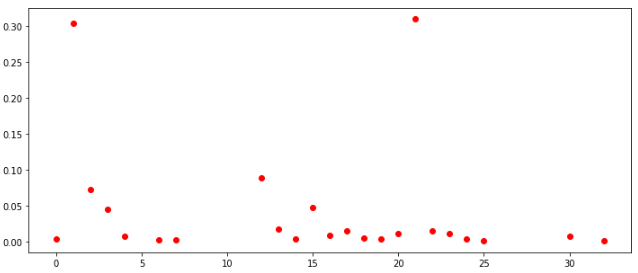
распределение чисел по ТОП-100
Если смотреть распределения по всем клеткам среди всех игроков, то выглядят они в целом похоже. Также можно сделать вывод, что в данных условиях нет смысла заполнять клетки значениями больше 30.
На этом исследование подходит к концу — это все, что я смог извлечь из этих данных. Возможно кто-то из вас сможет предложить что-то еще, что можно проверить — жду вас в комментариях. Обезличенные игры ищите по ссылке.
Пы.Сы. В предыдущем посте я рассказал про нейронку, которая обучалась играть в эту игру. К сожалению, ничего из этого пока не получилось. Две нейронки решили, что лучшая стратегия — кидать нули на выходе и радоваться ничьей. Но может я еще разберусь в этой теме и сделаю отдельный пост посвященный ошибкам, которые я допустил при создании нейронки, и, возможно, успехам.
Комментарии (7)

Luxo
26.02.2019 10:40Теория игр решает.
Не совсем понятно, что означает «идеальное решение». Обычно используется понятие оптимальной стратегии.
Грубо говоря, оптимальная стратегия существует. Это равновесие Нэша. Для таких игр — всегда)
Игроки присылали так называемые «чистые стратегии». А в чистых стратегиях равновесия Нэша для данной игры само собой нету.
Оно в смешанной стратегии. Это когда стратегия — это набор расстановок солдатиков, каждая из которых играется с определённой вероятностью.
Потому-то вы и получили какие-то «дурацкие» бессмысленные результаты. А не из-за того, что «идеального решения не существует».

Nevvy
26.02.2019 15:29+1Хотелось бы заметить, что, строго говоря, исследуемая игра — это даже не «игра Блотто», а «аукцион китайских палочек» (chopstick auction). Разница в том, что в игре Блотто цель игроков — выиграть как можно больше сражений, но нет цели выиграть больше, чем оппонент.
Аукцион китайских палочек в каноничном виде — это когда разыгрываются три китайские палочки, ставки на которые принимаются по отдельности, и каждый игрок желает выиграть две палочки из трёх. В контексте данной статьи есть девять полей, из которых каждый игрок желает выиграть на пяти. В отличие от игры Блотто, выигрыш на четырёх полях это не лучше для игрока, чем проигрыш на всех, и выигрыш на всех это не лучше, чем выигрыш на пяти.
Насколько мне известно, разница в выигрышах игроков в данном случае важнее (в контексте того, как выглядят равновесия), чем вид бюджетного ограничения (фиксированный размер армии в Блотто против линейных издержек, предполагаемых в аукционах).
Равновесия Нэша в аукционах китайских палочек всё ещё описываются смешанными стратегиями, но вид этих равновесий прямо-таки завораживает. Давно известное равновесие[1] для трёх палочек говорит, что одно из равновесий описывается стратегией, которая задаётся равномерным распределением на поверхности тетраэдра в пространстве ставок на три палочки. Недавно было найдено ещё одно равновесие[2] (всё ещё для трёх палочек), которое берёт тот же тетраэдр и превращает его во фрактал в духе треугольника Серпинского. Равновесная стратегия в этом случае предполагает равномерное распределение ставок на поверхности этого фрактала.
Всё это написано к тому, чтобы сказать, что с математической точки зрения эксперимент автора интереса представляет мало, потому что игра уже решена и решена элегантно. Но из-за того, насколько устрашающе выглядят равновесия, эксперимент интересен с точки зрения исследования человеческого поведения — едва ли кто-то из участников честно рандомизировал на поверхности того фрактала. В частности, интересна асимметрия между полями — что многие (и победители в том числе) ставят больше на центральное поле, пренебрегая нижними полями. То есть, в данной популяции оптимально пренебрегать центральным полем, борясь вместо него за какие-то из более крайних.
[1] Szentes, Balazs, and Robert W. Rosenthal. “Three-Object Two-Bidder Simultaneous Auctions: Chopsticks and Tetrahedra.” Games and Economic Behavior 44, no. 1 (July 2003): 114–33. (paywalled)
[2] Ewerhart, Christian. “A ‘Fractal’ Solution to the Chopstick Auction.” Economic Theory, 2017, 1–17.
Nicknameless Автор
26.02.2019 15:36Спасибо за такой подробный комментарий, будет что изучить (так как я недавно только начал изучать теорию игр).
Согласен, мне было больше интересно посмотреть как ведут себя люди в этой игре, попробовать найти какие-то закономерности в их стратегиях.


Vsevo10d
Нейросети легко найдут оптимум в задачах типа дилеммы заключенного, а человек алчен и азартен.
Nicknameless Автор
Ну тут скорее дело во мне, а не в нейронке
Так как я обучал:
Есть две одинаковых модели, они генерируют матрицы 3х3, считаем скор по ним (кол-во занятых клеток плюс ничья), по нему обновляем их веса. Мне кажется, что ошибка в функции потери у меня
neurocore
Нужно добавить «психопата», который случайные матрицы подкидывает. Мы же не в идеальном мире
axtrace
вспоминается история, когда ИИ-боты играли в шутер и пришли к выводу, что выгоднее стоять на месте и не стрелять друг в друга