Одна из проблем обучения нейронных сетей — переобучение. Это когда алгоритм научился хорошо работать с данными, которые он видел, а на других он справляется хуже. В статье мы рассказываем, как попытались решить эту проблему, совместив обучение градиентным спуском и эволюционным подходом.

Если кто-то хочет лучше понимать, о чем будет речь ниже, то можно прочитать эти статьи на хабре: статья1 и статья2
( далее добавление шума будем называть словом мутация, не потому что модно, а потому что в одно слово, а все зашумленные сети являются потомками родителя )
Мы решили учить спуском на одной части датасета, а эволюцией на другом, что в теории должно помочь модели улучшить обобщающую способность. Также у каждой части были разные функции для оптимизации.
В процессе у нас появилось несколько идей и гипотез, в следствие чего мы разделились на два независимых эксперимента с общей идей, но с разными подходами к эволюции. Первый эксперимент будет описан Егором, второй мной.
P.S. так как мы разводим потомков модели, чтобы выбрать лучшую и обучать ее дальше, чтобы снова сделать потомков и тд., то у меня возникла ассоциация со Спартой, где слабых детей выбрасывали, а других обучали как воинов. Поэтому назвали спартанским обучением.
Общая идея:
Инициализируем либо загружаем веса модели-родителя
- Обучаем N эпох модель-родителя
- Создаем K потомков разными мутациями
- Считаем фитнес-функцию по потомкам
- Объявляем нового родителя (об этом будет каждый эксперимент)
- goto 1
Общие детали эксперимента:
Датасет — CIFAR10
Модели — resnet18 с нуля и предобученная
Оптимизатор — SGD
Функция потери — CrossEntropyLoss
Функция оценки качества модели и ее потомков — accuracy
Мутации каждые 5 эпох
Обучение шло 50 эпох, эволюция засчитывалась за эпоху
На каждую мутацию 40-50 потомков
Примечание: в ходе обучения не использовались никакие дополнительные техники как уменьшение шага обучения, регуляризации и т.д.
Эксперимент №1. Метод случайных градиентов.
А в процессе того пока мы над этим работали это стало напоминать метод отжига.
Похожие штуки пробовали в статьях: Adding Gradient Noise Improves Learning for Very Deep Networks, Evolutionary Stochastic Gradient Descent for Optimization of Deep Neural Networks.
For i in range(N):
Обучаем N эпох модель-родителя
Градиентным методом с SGD
# часть с мутациями
For k in range(K):
Создаем потомка добавлением шума
Если он оказался лучше родителя делаем его родителем.В результате за счет части с мутациями у нас или улучшения или в худшем случае ничего не поменялось, если ни одно из прибавлений шума не улучшило модель.
А теперь Gо в детали.
Чтобы все заработало нужно было решить следующие вопросы:
- Было непонятно как выбирать лучшего потомка, по целевой метрике или по лоссу, ведь он тоже менялся.
- Как видно ниже (Картинка 1) улучшения не такие хорошие как хотелось бы. И в то время как скор за счет шума растет на трейне он каждый раз чуть — чуть падает на валидации. Делаем вывод что метод не работает?
- Просто добавление шума самом собой не заработало и пришлось много шаманить.
Сейчас я подробно расскажу про эти три пункта.
 |
|---|
| Картинка 1. Выбор лучшего потомка по accuracy. |
По какой метрике оценивать, по лоссу или по целевой. Мы попробовали и по лоссу и по целевой метрике accuracy в нашем случае, в результате, всегда работает только по лоссу. Вот еще пример где лучшего потомка выбирали по лоссу. (Картинка 2).
 |
|---|
| Картинка 2. Выбор лучшего потомка по лоссу. |
После мутаций метрика на валидации становится хуже.
Получалось что после каждого этапа мутаций скор падал на валидации? Делаем вывод что ничего не работает? Как оказалось все не так просто. При этом скор чуть чуть быстрее рос при проходе SGD на мутировавших (зашумленных) потомках. В итоге финальный скор был чуть лучше. Это было удивительно, приятно и абсолютно не понятно.
Буквально чуть лучше:
Accuracy 47.81% — наш велосипед с шумом.
Accuracy 47.72% — просто SGD.
Тут надо пояснить что этап с мутациями мы считали как одну эпоху. Мы делали 40 мутаций каждую пятую эпоху. Поэтому общее число итераций у SGD больше. Но при этом финальный скор все равно лучше.
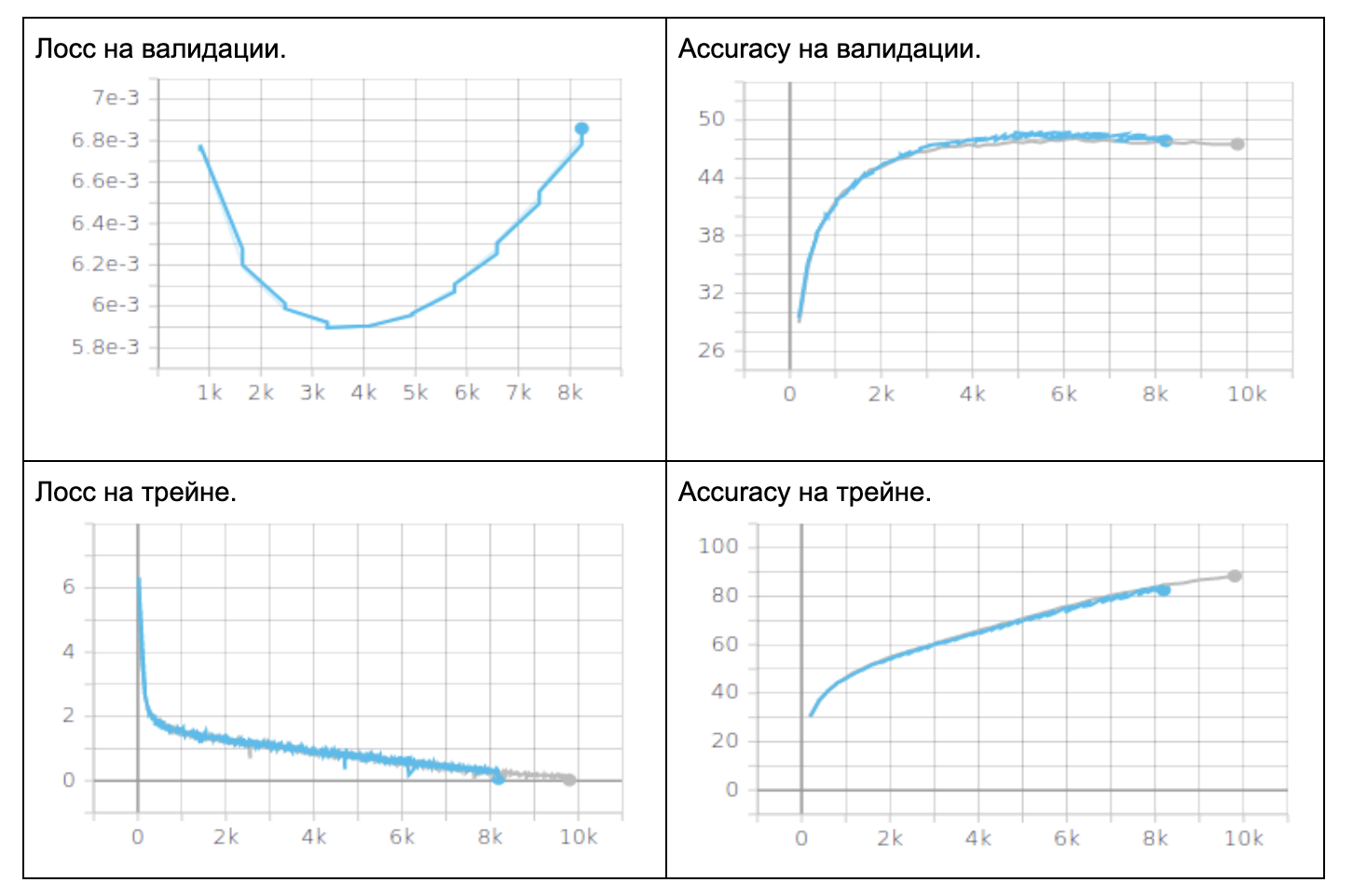 |
|---|
| Таблица 1. Метрика Аccuracy, resnet18, CIFAR10 на 10 классов, SGD. 40 мутаций каждую 5ю эпоху. Выбор лучшего потомка по лоссу. Серый график обучение SGD, синий график наш метод. |
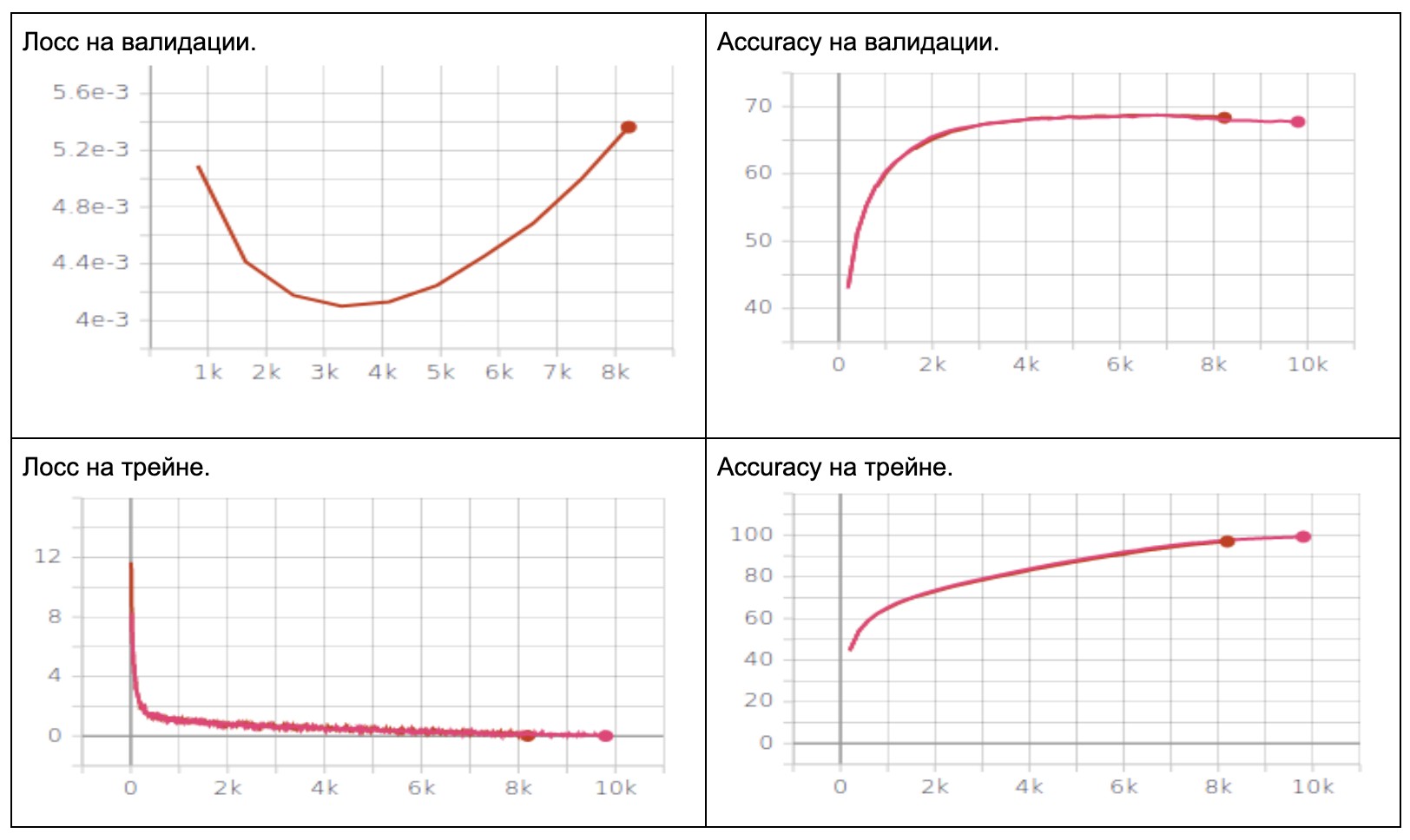 |
| :--: |
| Таблица 2. Метрика Аccuracy, предобученный resnet18, CIFAR10 на 10 классов, SGD. 40 мутаций каждую 5ю эпоху. Выбор лучшего потомка по accuracy. Розовый график обучение SGD, оранжевый график наш метод. |
В такой постановке мы сделали 4 эксперимента, предобученый и не предобученный resnet18 выбор потомка по лоссу и по accuracy. Улучшений не было на не предобученном при выборе потомка по accuracy. В остальных случаях было чуть чуть лучше.
А теперь о том как получилось заставить это работать. Собственно про шум.
Мы долго пробовали добавлять разный шум, но получалось с переменным успехом. В основном случайные шум очень редко улучшал лосс или целевую метрику, а чаще просто ухудшал.
В итоге мы решили добавлять не совсем случайный шум, а брать шум который был бы похож на шаг градиента.
Т.е. мы считали градиент, умножали его шум из равномерного распределения и на шаг обучения. И так обновляли веса. Еще мы ввели некоторый параметр температуры, что бы шаг обновления был тем меньше чем целевая метрика лучше.
Собственно поэтому этот велосипед мы и назвали метод случайных градиентов.
Плюсы:
- Итераций меньше, а скор чуть лучше.
- Это работает как регуляризация для вала. Во всех случаях скор на трейне у нас был всегда хуже, а на вале в итоге почти всегда лучше.
Минусы
- Много танцев с бубном ради очень маленького прироста. Появляется еще куча гипер параметров которые надо подбирать.
- Для шума нужно делать backward.
Эксперимент №2. Эволюционные стратегии
Для мутаций я использовал алгоритм описанный OpenAI в работе Evolution Strategies as a Scalable Alternative to Reinforcement Learning, реализация алгоритма была взята из репозитория https://github.com/staturecrane/PyTorch-ES
For i in range(N):
Обучаем N эпох модель-родителя с помощью SGD
For k in range(K):
Создаем потомка добавлением шума
Высчитываем его скор
Сохраняем потомка и его скор
Получаем нового родителяСоздание потомков
Создание потомков стандартно для эволюционных алгоритмов — к родительским весам прибавляется случайный шум. Шум генерировался равномерным распределением от -1 до 1 и умножался на ?, чтобы избежать большого разброса.
Получение нового родителя
normalized_rewards = (rewards - np.mean(rewards)) / np.std(rewards)
for index, param in enumerate(self.weights):
A = np.array([p[index] for p in population])
rewards_pop = torch.from_numpy(np.dot(A.T,normalized_rewards).T).float()
param.data = param.data + LEARNING_RATE/(POPULATION_SIZE * SIGMA) * rewards_popЗдесь уже начинается интересное. После вычисления фитнес-функции не выбирается лучший потомок. Скор каждого потомка нормализуется, после чего вектор нормализованных скоров умножается на шум. После чего прибавляется к родительским весам по формуле выше.
Результаты эксперимента
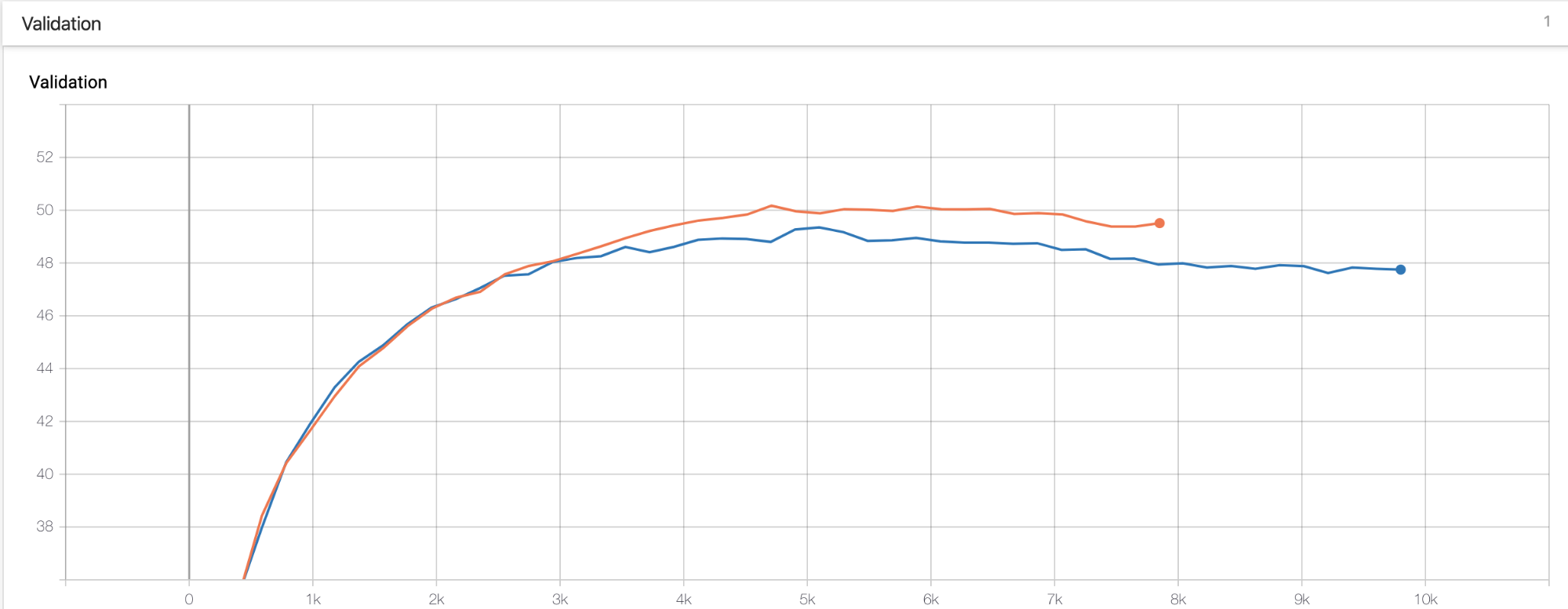
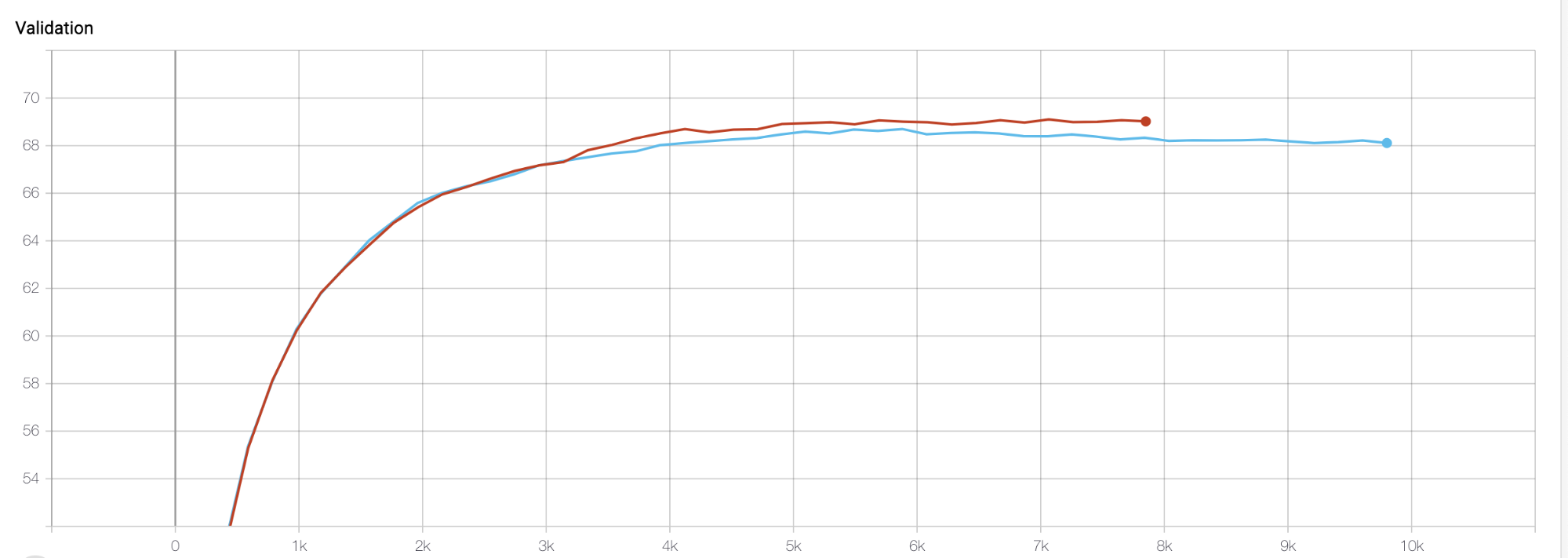
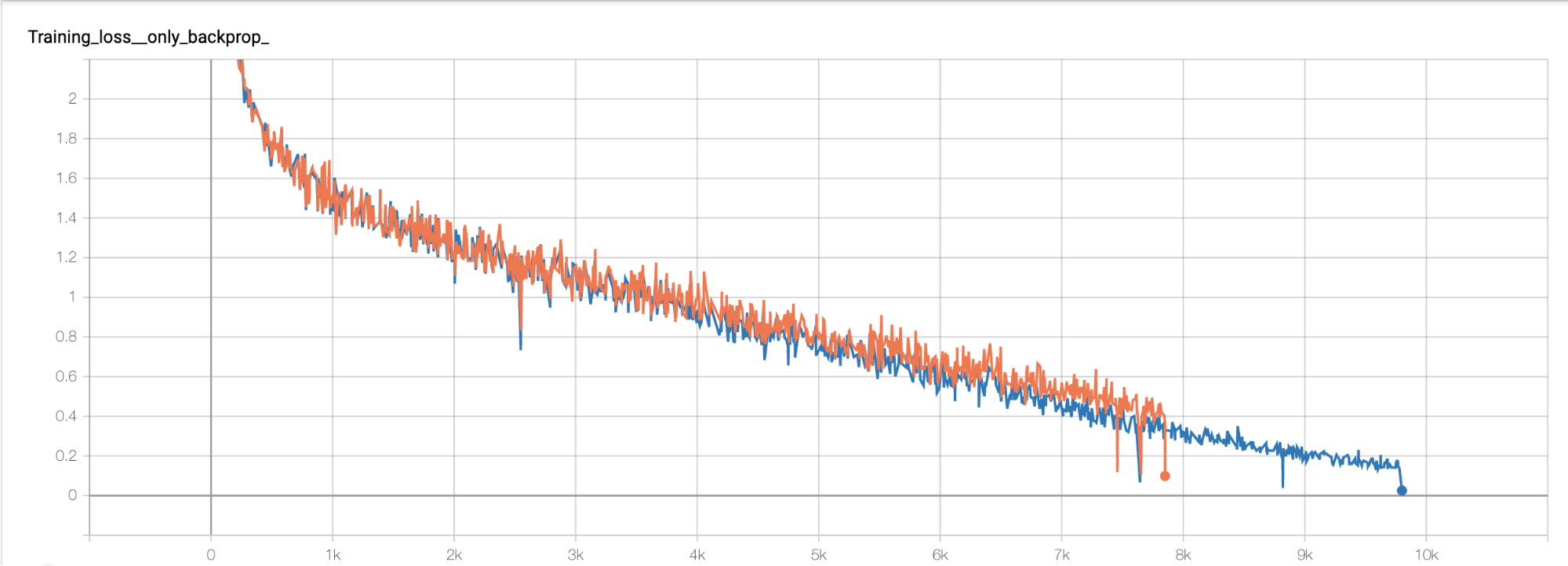
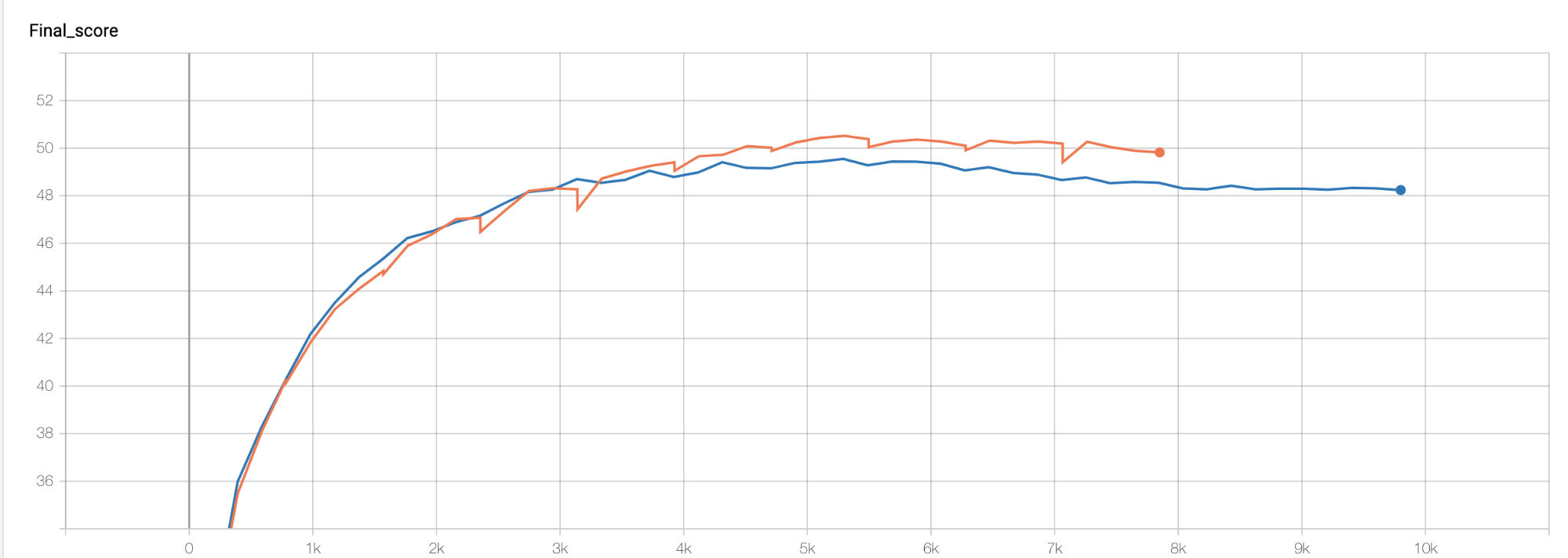
Рыжий/Красный — SGD+эволюция
Голубой/Синий — SGD
| C нуля | Pretrained |
|---|---|
 |
 |
 |
 |
 |
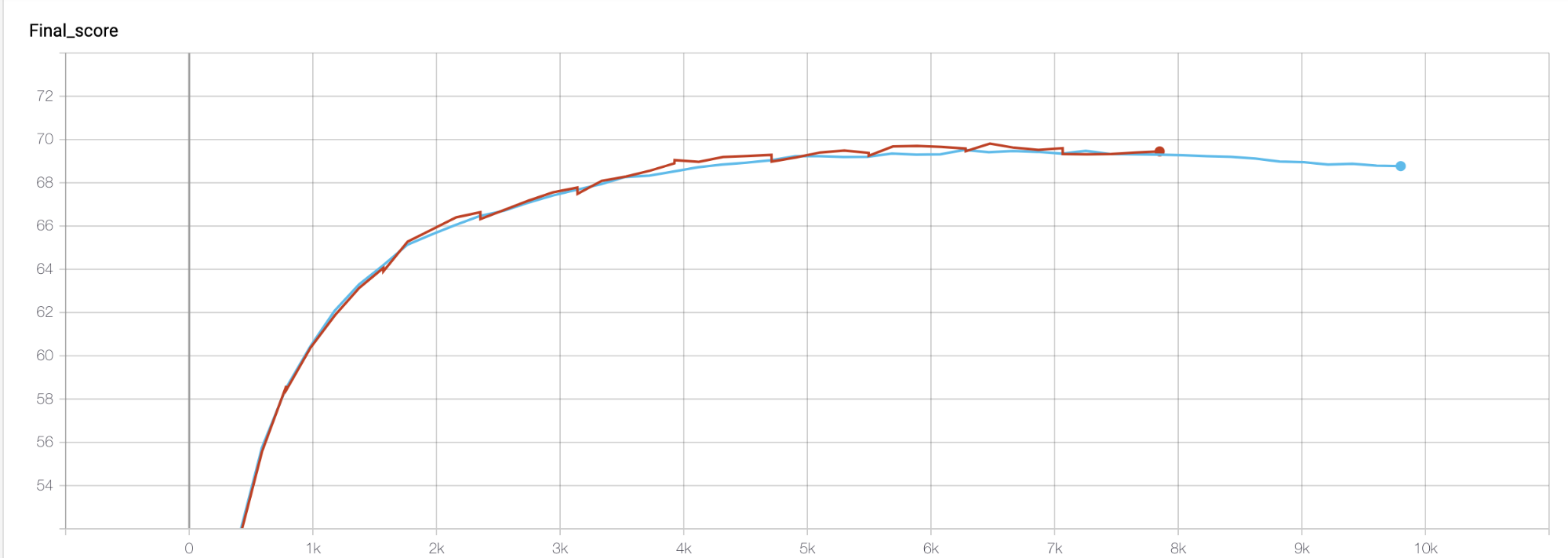 |
Loss — За время обучения после каждой эволюции значение функции всегда увеличивалось, что не удивительно. Поэтому на тренировочном датасете под конец обучения у классического SGD значение лучше, но для нас это не так важно, так как это не наша финальная метрика.
Validation — здесь можно посмотреть прогресс моделей на валидационном датасете по метрике accuracy. Можно заметить, что где-то на 5к итерации значение для варианта с классическим SGD стало падать, что говорит о том, что модель начала переобучаться на тренировочном датасете, когда как график SGD+эволюция продолжил расти
Final score — показывает рост метрики accuracy на тестовом датасете и здесь происходило примерно тоже самое, что и на валидации.
Вывод: использование эволюционной стратегии в связке с SGD позволило избежать проблем с переобучением и на тестовом датасете дало наибольший скор как при обучении с нуля, так и при обучении c предобученной моделью.
Думаю, если бы было больше потомков на шаге эволюции, то и результат был бы лучше, но тут уже идет вопрос о доступных мощностях и скорости обучения, так как обучать несколько тысяч потомков в данный момент позволяют себе только Google и другие корпорации.
Финальная таблица по accuracy на тесте
| С нуля | Pretrained | |
|---|---|---|
| SGD | 47.72% | 68.56 % |
| Метод случайных градиентов | 47.81% | 68.61 % |
| SGD + эволюционная стратегия от OpenAI | 49.82% | 69.45 % |
Итог:
- Не удалось заставить работать с Adam, возможно, у нас просто закончился энтузиазм. Во всех экспериментах с ним эволюционные методы чуть чуть проигрывали.
- Можно было сделать мутации частью оптимизатора, а не писать отдельную оболочку для этого
- Ушло в несколько раз больше времени, чем мы планировали
Будем рады обратной связи не только по контенту, но и по самой статье в целом. Если занимаетесь этой темой или интересовались, то тоже пишите, было бы здорово пообщаться, может мы что-то упустили.
Полезные ссылки


Undiabler
Спасибо, интересный эксперимент.
А откуда вы взяли формулу «Получение нового родителя»? Честно говоря очень спорный подход с увеличением весов по общему движению всей популяции.
В данном случае логичнее брать некий персентиль лучших потомков, а не всю популяцию. В вашем случае выходит что не отсеиваются худшие потомки, а подавляются веса в среднем если получилась плохая популяция.
Nicknameless Автор
Формулу взял из статьи OpenAI Evolution Strategies as a Scalable Alternative to Reinforcement Learning
Думаю действительно стоит проверить на какой-то части лучших потомков
Спасибо за совет