Как правило, модификации алгоритмов, полагающиеся на особенности конкретной задачи, считаются менее ценными, так как их сложно обобщить на более широкий класс задач. Однако это не означает, что такие модификации не нужны. Более того, часто они могут значительно улучшить результат даже для простых классических задач, что очень важно при практическом применении алгоритмов. В качестве примера в этом посте я решу задачу Mountain Car при помощи обучения с подкреплением и покажу, что используя знание о том, как устроена задача, ее можно решить значительно быстрее.

О себе

Меня зовут Олег Свидченко, сейчас я учусь в Школе физико-математических и компьютерных наук Питерской Вышки, до этого три года учился в СПбАУ. Также я работаю в JetBrains Research в качестве исследователя. До поступления в университет я учился в СУНЦ МГУ и стал призером Всероссийской олимпиады школьников по информатике в составе сборной Москвы.

Что нам потребуется?

Если вам интересно попробовать позаниматься обучением с подкреплением, задача Mountain Car отлично для этого подходит. Сегодня нам потребуется Python с установленными библиотеками Gym и PyTorch, а также базовые знания о нейронных сетях.

Описание задачи

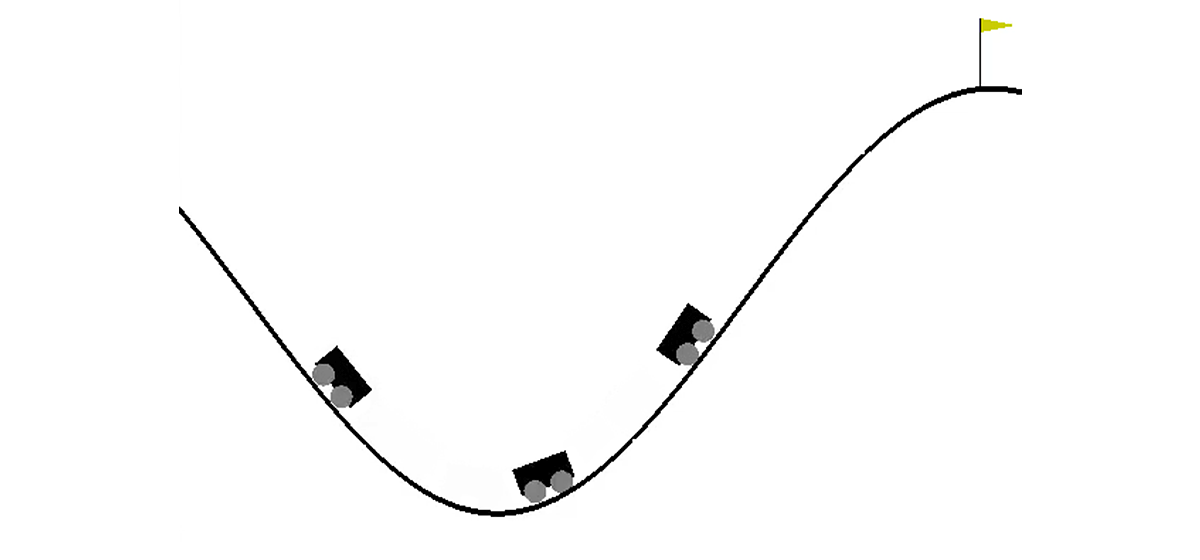
В двумерном мире машине нужно подняться из впадины между двумя холмами на вершину правого холма. Все усложняет тот факт, что ей не хватает мощности двигателя, чтобы преодолеть силу гравитации и въехать туда с первой попытки. Нам предлагается обучить агента (в нашем случае — нейронную сеть), который сможет, управляя ею, подняться на правый холм как можно быстрее.

Управление машиной осуществляется посредством взаимодействия со средой. Оно делится на независимые эпизоды, а каждый эпизод осуществляется пошагово. На каждому шаге агент получает из окружения состояние s и награду r в ответ на совершенное им действие a. Кроме того, иногда среда может дополнительно сообщить, что эпизод закончился. В данной задаче s — пара чисел, первое из которых — положение автомобиля на кривой (одной координаты достаточно, так как мы не можем оторваться от поверхности), а второе — его скорость на поверхности (со знаком). Награда r — число, всегда равное -1 для этой задачи. Таким образом, мы поощряем агента завершить эпизод как можно быстрее. Возможных действий всего три: толкать машину налево, ничего не делать и толкать машину направо. Этим действиям соответствуют числа от 0 до 2. Эпизод может завершиться в случае, если автомобиль достиг вершины правого холма или в случае, если агент сделал 200 шагов.

Немного теории

На Хабре уже была статья о DQN, в которой автор довольно хорошо описал всю необходимую теорию. Тем не менее для удобства чтения я повторю ее здесь в более формальном виде.

Задача обучения с подкреплением задается набором из пространства состояний S, пространства действий A, коэффициента $$, функции перехода T и функции награды R. В общем случае функция перехода и функция награды могут быть случайными величинами, однако сейчас мы рассмотрим более простой вариант, в котором они являются однозначно определенными. Цель заключается в том, чтобы максимизировать кумулятивную награду $$, где t — номер шага в среде, а T — количество шагов в эпизоде.

Чтобы решить эту задачу, определим value-функцию V от состояния s как значение максимальной кумулятивной награды при условии, что мы начинаем в состоянии s. Зная такую функцию, мы можем решить задачу просто каждым шагом переходя в s с максимально возможным значением. Однако не все так просто: в большинстве случаев мы не знаем какое действие приведет нас в нужное состояние. Поэтому добавим действие a в качестве второго параметра функции. Полученная функция называется Q-функцией. Она показывает, какую максимально возможную кумулятивную награду мы можем получить, совершив действие a в состоянии s. А вот эту функцию мы уже можем использовать для решения задачи: находясь в состоянии s просто выберем такое a, что Q(s, a) максимальна.

На практике мы не знаем настоящую Q-функцию, но зато можем ее приблизить различными методами. Одним из таких методов является Deep Q Network (DQN). Его идея заключается в том, что мы для каждого из действий приближаем Q-функцию при помощи нейронной сети.

Окружение

Теперь перейдем к практике. Для начала нам нужно научиться эмулировать среду MountainCar. С этой задачей нам поможет справиться библиотека Gym, которая предоставляет большое количество стандартных окружений для обучения с подкреплением. Чтобы создать среду нам нужно вызвать метод make у модуля gym передав ему название желаемой среды в качестве параметра:

import gym
env = gym.make("MountainCar-v0")

Подробную документацию можно посмотреть здесь, а описание среды — здесь.
Рассмотрим подробнее то, что мы можем делать с созданной нами средой:

• env.reset() — завершает текущий эпизод и начинает новый. Возвращает начальное состояние.
• env.step(action) — совершает указанное действие. Возвращает новое состояние, награду, завершился ли эпизод и дополнительную информацию, которую можно использовать для дебага.
• env.seed(seed) — устанавливает random seed. От него зависит то, как будут генерироваться начальные состояния во время env.reset().
• env.render() — отображает текущее состояние среды.

Реализуем DQN

DQN — алгоритм, который использует нейронную сеть для оценки Q-function. В оригинальной статье DeepMind определили стандартную архитектуру для Atari игр используя сверточные нейронные сети. В отличии от этих игр, Mountain Car не использует изображение в качестве состояния, поэтому архитектуру нам придется определять самим.

Возьмем, например, архитектуру с двумя скрытыми слоями по 32 нейрона в каждом. После каждого скрытого слоя будем использовать ReLU в качестве функции активации. На вход нейронной сети подаются два числа, описывающие состояние, а на выходе мы получаем оценку Q-функции.

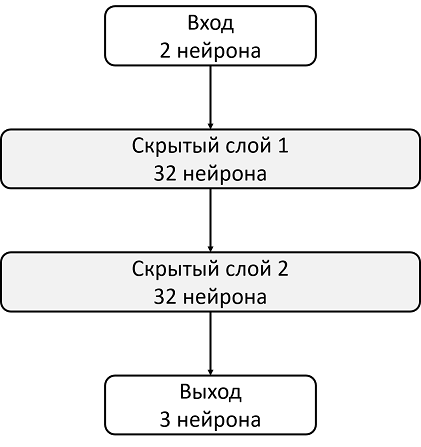
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(2, 32),
    nn.ReLU(),
    nn.Linear(32, 32),
    nn.ReLU(),
    nn.Linear(32, 3)
)

target_model = copy.deepcopy(model)
    
#Инициализация весов нейронной сети
def init_weights(layer):
    if type(layer) == nn.Linear:
       nn.init.xavier_normal(layer.weight)

model.apply(init_weights)

Поскольку обучать нейронную сеть мы будем на GPU, то нам необходимо загрузить туда нашу сеть:

# Если хотим обучать на CPU, то “cuda” нужно заменить на “cpu”
device = torch.device("cuda")
model.to(device)
target_model.to(device)

Переменная device будет глобальной, так как данные нам тоже нужно будет загружать.

Также нам нужно определить оптимизатор, который будет обновлять веса модели используя градиентный спуск. Да, их существует сильно больше, чем один.

optimizer = optim.Adam(model.parameters(), lr=0.00003)

Теперь объявим функцию, которая будет считать функцию ошибки, градиент по ней, и применять спуск. Но перед этим необходимо загрузить данные из батча на GPU:

state, action, reward, next_state, done = batch
# Загружаем батч на выбранное ранее устройство
state = torch.tensor(state).to(device).float()
next_state = torch.tensor(next_state).to(device).float()
reward = torch.tensor(reward).to(device).float()
action = torch.tensor(action).to(device)
done = torch.tensor(done).to(device)

Далее нам нужно посчитать реальные значения Q-function, однако поскольку мы их не знаем, то мы их оценим через значения для следующего состояния:

target_q = torch.zeros(reward.size()[0]).float().to(device)
with torch.no_grad():
    # Выбираем максимальное из значений Q-function для следующего состояния
    target_q[done] = target_model(next_state).max(1)[0].detach()[done]
target_q = reward + target_q * gamma

И текущее предсказание:

q = model(state).gather(1, action.unsqueeze(1))

С помощью target_q и q считаем функцию потерь и обновляем модель:

loss = F.smooth_l1_loss(q, target_q.unsqueeze(1))
# Очищаем текущие градиенты внутри сети
optimizer.zero_grad()
# Применяем обратное распространение  ошибки
loss.backward()
# Ограничиваем значения градиента. Необходимо, чтобы обновления не были слишком большими
for param in model.parameters():
   param.grad.data.clamp_(-1, 1)
# Делаем шаг оптимизации
optimizer.step()

Поскольку модель лишь считает Q-функцию, а не совершает действия, то нам необходимо определить функцию, которая будет решать, какие именно действия агент будет совершать. В качестве алгоритма принятия решений мы возьмем $$-greedy политику. Ее идея заключается в том, что агент обычно совершает действия жадно, выбирая максимум Q-функции, однако с вероятностью $$ он совершит случайное действие. Случайные действия нужны для того, чтобы алгоритм мог исследовать те действия, которые он бы не совершил руководствуясь лишь жадной политикой — этот процесс называется exploration.

def select_action(state, epsilon, model):
    if random.random() < epsilon:
        return random.randint(0, 2)
    return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item()

Поскольку для обучения нейронной сети мы используем батчи, то нам понадобится буфер, в котором мы будем хранить опыт взаимодействия со средой и откуда мы будем выбирать батчи:

class Memory:
    def __init__(self, capacity):
        self.capacity = capacity
        self.memory = []
        self.position = 0

    def push(self, element):
        """Сохраняет элемент в циклический буфер"""
        if len(self.memory) < self.capacity:
            self.memory.append(None)
        self.memory[self.position] = element
        self.position = (self.position + 1) % self.capacity

    def sample(self, batch_size):
        """Возвращает случайную выборку указанного размера"""
        return list(zip(*random.sample(self.memory, batch_size)))
    
    def __len__(self):
        return len(self.memory)

Наивное решение

Для начала объявим константы, которые будем использовать в процессе обучения, и создадим модель:

#Количество обновлений model между обновлениями target model
target_update = 1000
#Размер одного батча, который на вход принимает модель
batch_size = 128
#Количество шагов среды
max_steps = 100001
#Границы коэффициента exploration
max_epsilon = 0.5
min_epsilon = 0.1

#Создаем модель и буфер
memory = Memory(5000)
model, target_model, optimizer = create_new_model()

Несмотря на то, что процесс взаимодействия было бы логично разделить на эпизоды, для описания процесса обучения нам удобнее разделить его на отдельные шаги, так как мы хотим после каждого шага среды делать один шаг градиентного спуска.

Поговорим подробнее о том, как у нас выглядит один шаг обучения. Будем считать, что сейчас мы совершаем шаг с номером step из max_steps шагов и текущим состоянием state. Тогда совершение действия при помощи $$-greedy политики будет выглядеть так:

epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps
action = select_action(state, epsilon, model)
new_state, reward, done, _ = env.step(action)

Сразу добавим полученный опыт в память и начнем новый эпизод, если текущий закончился:

memory.push((state, action, reward, new_state, done))
if done:
      state = env.reset()
      done = False
else:
      state = new_state

И сделаем шаг градиентного спуска (если, конечно, уже можем собрать хотя бы один батч):

if step > batch_size:
     fit(memory.sample(batch_size), model, target_model, optimizer)

Теперь осталось обновить target_model:

if step % target_update == 0:
      target_model = copy.deepcopy(model)

Однако нам бы хотелось еще и следить за процессом обучения. Для этого мы будем играть дополнительный эпизод после каждого обновления target_model с epsilon = 0, запоминая суммарную награду в буфер rewards_by_target_updates:

if step % target_update == 0:
      target_model = copy.deepcopy(model)
      
      state = env.reset()
      total_reward = 0
      while not done:
            action = select_action(state, 0, target_model)
            state, reward, done, _ = env.step(action)
            total_reward += reward

      done = False
      state = env.reset()
      rewards_by_target_updates.append(total_reward)

Запустим этот код и получим примерно такой график:

Что пошло не так?

Это баг? Это неправильный алгоритм? Это плохие параметры? Не совсем. На самом деле, проблема в задаче, а именно в функции награды. Посмотрим на нее внимательнее. На каждом шаге наш агент получает награду -1, и так происходит до тех пор, пока не завершится эпизод. Такая награда мотивирует агента завершить эпизод как можно быстрее, но в то же время не подсказывает ему как это сделать. Из-за этого единственный способ научиться решать задачу в такой постановке для агента — решить ее много раз, при помощи exploration.

Конечно, можно было бы попробовать применить более сложные алгоритмы для исследования среды вместо нашей $$-greedy политики. Однако, во-первых, из-за их применения наша модель станет более сложной, чего хотелось бы избежать, а во-вторых, не факт, что они будут работать достаточно хорошо для данной задачи. Вместо этого мы можем устранить источник проблемы, модифицировав саму задачу, а именно изменив функцию награды, т.е. применив то, что называется reward shaping.

Ускоряем сходимость

Наше интуитивное знание подсказывает нам, что чтобы заехать на холм нужно разогнаться. Чем больше скорость, тем ближе агент к решению задачи. Можно сообщить ему об этом, например, добавив модуль скорости с некоторым коэффициентом к награде:

modified_reward = reward + 10 * abs(new_state[1])

Соответственно, строчку в функции fit

memory.push((state, action, reward, new_state, done))

следует заменить на

memory.push((state, action, modified_reward, new_state, done))

Теперь посмотрим на новый график (на нём представлена оригинальная награда без модификаций):


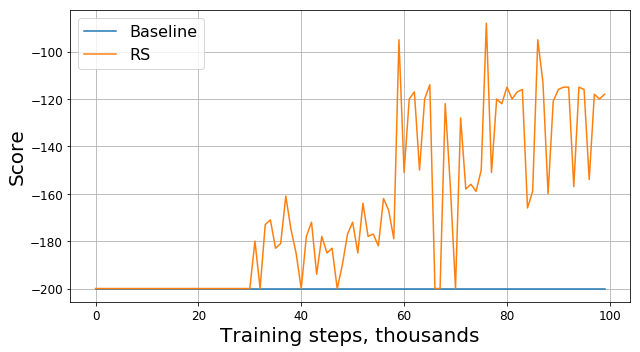
Здесь RS — это сокращение от Reward Shaping.

А хорошо ли так делать?

Прогресс очевиден: наш агент явно научился заезжать на холм, поскольку награда стала отличаться от -200. Остался только один вопрос: если изменив функцию награды, мы изменили и саму задачу, будет ли найденное нами решение новой задачи хорошим для старой задачи?

Для начала поймем, что означает «хорошесть» в нашем случае. Решая задачу, мы пытаемся найти оптимальную политику — такую, которая максимизирует суммарную награду за эпизод. В таком случае мы можем заменить слово «хорошее» на слово «оптимальное», поскольку его-то мы и ищем. Также мы оптимистично надеемся, что наш DQN рано или поздно найдет оптимальное решение для модифицированной задачи, а не застрянет в локальном максимуме. Итак, вопрос можно переформулировать следующим образом: если изменив функцию награды, мы изменили и саму задачу, будет ли найденное нами оптимальное решение новой задачи оптимальным для старой задачи?

Как оказывается, мы не можем предоставить такой гарантии в общем случае. Ответ зависит от того, как именно мы изменили функцию награды, как она была устроена раньше и как устроена сама среда. К счастью, есть статья, авторы которой исследовали то, как изменение функции награды влияет на оптимальность найденного решения.

Во-первых, они нашли целый класс «безопасных» изменений, которые основаны на методе потенциалов: $$, где $$ — потенциал, который зависит только от состояния. Для таких функций авторы смогли доказать, что если решение для новой задачи оптимально, то и для старой задачи оно также оптимально.

Во-вторых, авторы показали, что для любой другой $$ существует такая задача, функция награды R и оптимальное решение измененной задачи, что это решение не является оптимальным для исходной задачи. Это значит, что мы не можем гарантировать хорошесть найденного нами решения если используем изменение, которое не основано на методе потенциалов.

Таким образом, использование потенциальных функций для модификации функции награды может изменить только скорость сходимости алгоритма, но не влияет на итоговое решение.

Ускоряем сходимость правильно

Теперь, когда мы знаем, как можно безопасно изменять награду, попробуем модифицировать задачу еще раз, используя метод потенциалов вместо наивной эвристики:

modified_reward = reward + 300 * (gamma * abs(new_state[1]) - abs(state[1]))

Посмотрим на график оригинальной награды:



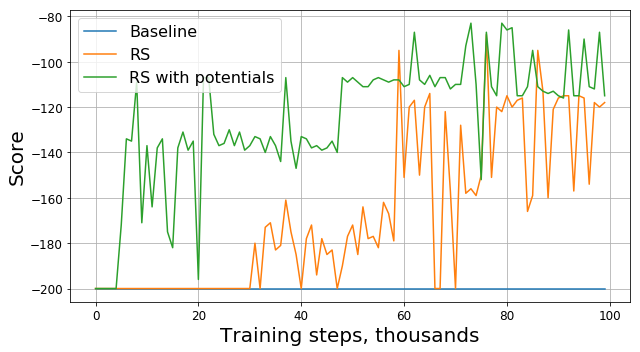
Как оказалось, помимо наличия теоретических гарантий, модификация награды при помощи потенциальных функций также значительно улучшила результат, особенно на ранних этапах. Конечно, есть вероятность, что можно было бы подобрать более оптимальные гиперпараметры (random seed, gamma и остальных коэффициентов) для обучения агента, однако reward shaping все равно они значительно увеличивает скорость сходимости модели.

Послесловие

Спасибо, что дочитали до конца! Надеюсь, что вам понравился этот небольшой практикоориентированный экскурс в обучение с подкреплением. Понятно, что Mountain Car — «игрушечная» задача, однако, как мы смогли заметить, научить агента решать даже такую на первый взгляд простую с точки зрения человека задачу может быть непросто.