Переосмыслить концепцию задачи тяжело, но результат стоит того

Примечание автора: я знаю, что неправильно вычислил перенос Брэгга как в классическом, так и в квантовом случае; однако, это достаточно близко к правде для того, чтобы понять разницу между программированием классического и квантового компьютера.
Время: где-то в 2018 году. Место: тухлый канал в Слаке.
«Ты знаешь Python?»
Вопросы Джона Тиммера, научного директора Ars Technica, иногда могут застать врасплох. Если бы в Слаке можно было пропитывать буквы осторожностью, то мой ответ «Да» просто сочился бы ею.
Оказывается, что D-Wave решила дать всему миру доступ к своему квантовому оптимизатору через API. Ars пригласили его опробовать, но нужно было знать Python. Я был готов на это.
Я предполагал, что D-Wave выпустит какой-то фантастический API, который сможет взять мой фирменный код, заставляющий программистов рыдать, и превратит его в квантово-оптимизированные строчки. Увы, когда я добрался до квантового оптимизатора, оказалось, что это не так. Я быстро оказался погружённым в документацию, пытаясь выяснить, что мне вообще нужно делать.
Думаю, что представитель D-Wave по связям с общественностью имел в виду человека, знавшего достаточно для того, чтобы запускать уже готовые примеры. Но я упрям. Мне нужно было придумать три-четыре возможных задачи, которые я хотел проверить. Я хотел выяснить: смогу ли я овладеть процессом решения этих задач на компьютере D-Wave? Насколько легко совершить концептуальный скачок от классического программирования до работы с квантовым отжигом? Подойдут ли вообще хоть какие-то из моих задач к этой машине?
Раскрывая потрясающий вывод прямо сразу, скажу, что ответы получились следующими: может, не совсем «овладеть»; сложно; не все задачи.
Выбор задач для программирования
Несмотря на то, как вы меня себе представляете, меня можно назвать практикующим программистом. По сути, любой человек, достаточно хорошо разбирающийся в программировании, поморщился бы (и, возможно, совершил бы убийство), увидев мой код на Python.
Однако я могу придумать задачи, требующие написания программы для их решения. Мне нужно, к примеру, что-то, вычисляющее электрическое поле набора электродов. Что-то, находящее состояние с минимальной энергией атома гелия. Или что-то, подсчитывающее рост интенсивности света при старте лазера. Эти задачи больше всего меня интересуют. И, начав этот проект, я понятия не имел, может ли архитектура D-Wave решить эти проблемы.
Я выбрал две проблемы, которые, по моему мнению, могли сработать: нахождение членов множества Мандельброта и расчёт потенциальных контуров набора электродов. Преимуществом этих проблем было то, что я мог быстро решить их при помощи классического кода, и сравнить ответы. Но я быстро столкнулся с проблемами, пытаясь понять, как запустить решение этих задач на машине от D-Wave. Тут требуется серьёзный сдвиг в осмыслении задач, а моё мышление работает довольно прямолинейно.
К примеру, одна из проблем, с которыми я сталкивался, состоит в том, что мы имеем дело с низкоуровневыми двоичными числами (несмотря на то, что они выражены в виде кубитов, а не битов). Это значит, что, по сути, в программе нет типов. Практически весь мой опыт в программировании заключается в решении физических задач при помощи числовых типов с плавающей точкой.
Приходится думать о задаче по-другому: ответ должен выражаться как двоичное число (в идеале, true или false), а вся физика (к примеру, все числа с плавающей запятой) должны выражаться через объединение кубитов. Даже если бы от этого зависела моя жизнь, я бы не смог разобраться, как это можно сделать для любой из моих задач. Погрузившись в преподавание, я позволил этой проблеме немного повариться в собственном соку.
Шесть месяцев спустя я, наконец, наткнулся на проблему, с которой я был знаком, и которую я мог бы решить при помощи компьютера D-Wave. Прохождение света сквозь волоконную брэгговскую решётку можно выразить в виде двоичной задачи: вышел фотон из фильтра, или нет? Вся физика содержится в соединениях кубитов, а ответ извлекается из энергии решения.
Брэгговские решётки
Одномерная брэгговская решётка – это многослойный материал. Каждый промежуток между двумя слоями отражает небольшое количество света. Общее проникновение через всю структуру определяется расстоянием между промежутками. Чтобы свет прошёл насквозь, необходимо, чтобы волны от различных промежутков складывались по фазе. Спектр прохода идеальной брэгговской решётки с 50 слоями и отражающей способностью в 0,1% показан ниже.
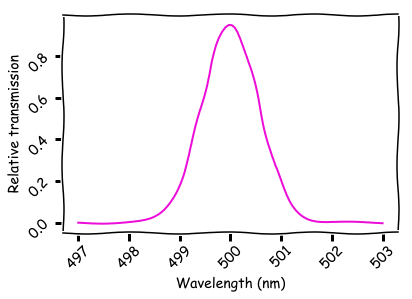
Следующий код генерирует данные для этого графика:
ld = np.linspace(ld_center-3e-9, ld_center+3e-9, num_ld)
k = 2*np.pi/ld
T = np.ones(ld.shape)
for j in range(num_layers):
T = T*(1-A)*np.cos(j*k*layer_sep)**2Здесь мы явно подсчитываем относительные вклады каждого промежутка, выраженные в оптической мощности, которые доходят до следующего промежутка. Конструктивная и деструктивная интерференции учитываются через уменьшение или увеличение вклада промежутка, в зависимости от того, насколько близко расстояние между слоями совпадает с половиной длины волны.
Этот хак необходим, поскольку соединение кубитов выражается только в действительных, а не в комплексных числах (физику лучше всего выражать через комплексные числа, содержащие амплитуду и фазу света). Тем не менее, вывод классического кода выглядит примерно правильным – немного беспокоит отсутствие боковых полос частот, что говорит о неполноте модели, но пока это неважно.
В классическом коде модели не хватает проверок на непротиворечивость. Я подсчитывал результат, предполагая, каким именно образом будет распространяться волна. Даже если это предположение окажется неверным, результат подсчёта будет тем же – хотя все уравнения основаны на физике, в коде невозможно гарантировать, что они правильно её описывают.
Переходим к квантам
В систему D-Wave необходимо создать цепочку кубитов, каждый из которых представляет интенсивность света на промежутке. Каждый кубит связан с соседями, и вес связи представляет проход от одного промежутка к другому, учитывающий расстояние между интерфейсами. Если расстояние между интерфейсами равно половине длины волны, свет может резонировать между двумя интерфейсами и проходить далее. Если расстояние равно четверти длины волны, срабатывает деструктивная интерференция, и связь должна быть минимальной.
Прохождение через один промежуток обозначается в 99,9%, поэтому соединение между нулевым и первым кубитом равно
Между первым и вторым:
Между вторым и третьим:
В этой формуле d обозначает физическое расстояние между слоями, а ? — длину волны. Если d/? = 0,5, тогда косинус равен единице, и мы можем надеяться на идеальное прохождение света.
В системе D-Wave это означает, что каждые два соседних кубита должны соединяться так:
В данном выражении степень u учитывает влияние предыдущих кубитов и упрощает схему соединения.
Внедрение задачи
Теперь, зная, как соединять кубиты, мы должны посмотреть на физическую связь кубитов, чтобы решить, как оформить эту задачу. Это называется малым внедрением [minor embedding].
Мы должны дать компьютеру список связей между кубитами с их весами. Мы также должны задать отклонения, обозначающие важность каждого кубита. В нашем случае все кубиты одинаково важны, поэтому они задаются как -1 для всех кубитов (это число я взял из стандартного примера). Отклонения и связи необходимо ассоциировать с физическими кубитами и связями между ними. В случае крупных задач поиск такого отображения может занять много времени.
Код для генерации связей и отклонений довольно прост.
#qubit labels (q[j], q[j]) используются как ключи в словаре связей
linear.update({(q[j], q[j]): -1}) # отклонения одинаковы
#у ближайших соседей связь ненулевая
if j-k == -1:
quad.update({(q[j], q[k]): (J_vals[j])**k})
#все остальные связи нулевые
else:
quad.update({(q[j], q[k]): 0})К счастью, API D-Wave попытается найти малое внедрение самостоятельно. Я обнаружил, что оно сработало для фильтра с 50 слоями, но не смогло справиться с 100 слоями. Мне это кажется довольно странным, поскольку имея 2000 кубитов и длину цепочки, равную 1 (нам не нужно комбинировать несколько физических кубитов для создания одного логического), система должна уметь внедрять и более крупные проблемы. Оглядываясь назад, я считаю, что неудача была связана с тем, что я задал слишком много нулевых связей.
Альтернативный подход – просто не определять явно нулевые связи. Это даёт алгоритму свободу в нахождении большего количества вариантов внедрения, где у кубитов нет связей. Я это не пробовал, но мне этот вариант кажется следующим логичным шагом.
В любом случае, запустить машину D-Wave очень просто:
response = EmbeddingComposite(DWaveSampler()).sample_qubo(Q_auto, num_reads=num_runs)Учимся говорить по-кубитски
Разница между моим классическим алгоритмом и решением от D-Wave состоит в том, что компьютер D-Wave не возвращает напрямую понятный результат. Он получается разбитым на много частей. Мы получаем список энергий, и самая маленькая из них должна быть решением. Для нескольких прогонов (допустим, 1000) для каждой энергии мы получаем количество раз, которое она появлялась в ответе. И для каждого прогона мы получаем «ответ», значение кубитов. Мне не сразу было ясно, какие из этих значений можно (и можно ли) интерпретировать как проход сквозь фильтр.
В итоге я решил, что лучше всего будет представлять ответ минимальная энергия решения, поскольку эта величина в каком-то смысле представляет количество энергии, хранящееся в фильтре. Поэтому решение с большей энергией представляет большую проницаемость фильтра, как показано ниже. Превращение этого ответа в реальное прохождение света оставляем в качестве домашнего задания для тех, кто в этом разбирается.

Также возможно получить физическое представление процесса, изучив значения кубитов при решении с наименьшей энергией. Ниже можно видеть битовые значения решений, соответствующих пику кривой передачи (500 нм), 50%-й передаче (500,6 нм) и 5%-й передаче (501,4 нм).
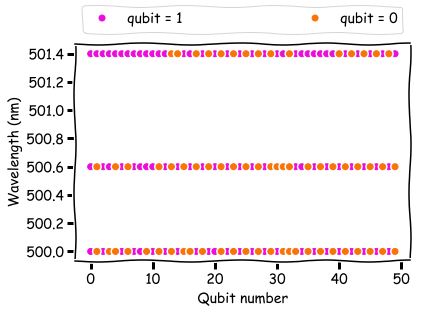
На краю пика передачи кубиты имеют тенденцию скапливаться в группы единиц. На пике кубиты чередуют 0 и 1. Это последнее решение – двоичная картина того, как варьируется интенсивность света в брэгговской решётке. Иначе говоря, решение D-Wave ещё и представляет физику напрямую, чего не скажешь о моём классическом коде.
В этом и заключается реальная сила квантового отжига. Да, я могу прекрасно вывести кривую прохождения через фильтр и из классических вычислений. Но чтобы получить картину реально происходящего внутри, нужен более сложный код. А в квантовом отжиге это достаётся совершенно бесплатно. По-моему, это весьма круто.
Ещё одно преимущество квантового отжига – он гарантирует непротиворечивость решения в рамках моего выбора весов связей кубитов. Это значит, что решение квантового компьютера, вероятно, будет более надёжным, чем решение, полученное из классического кода.
Рассуждения о квантовом программировании
Тяжелее всего в программировании машины D-Wave то, что для этого необходимо по-другому мыслить о задачах. Я, к примеру, привык к задачам по минимизации, когда кривая совпадает с данными. Но я нашёл весьма сложным сменить способ мышления о физической задаче так, чтобы начать писать код для её решения. Не помогает и то, что большинство примеров, данных компанией, для меня выглядят абстрактными и не адаптируемыми к физическим задачам. Но эта ситуация поменяется, когда всё больше пользователей начнут публиковать свой код.
Также сложности могут возникнуть с интерпретацией ответа. В принципе, мне понравилась простота API, и очень здорово получать дополнительные идеи бесплатно. В ближайшем будущем я бы мог использовать D-Wave для решения реальных задач.

