Итак, вот определение схем, не зависящих от скорости.

Класс (эквивалентности) это полное множество допустимых состояний схемы такое, что для любого состояния из этого множества существует последовательность допустимых состояний, начинающаяся с данного состояния и содержащая все состояния данного множества. Иными словами, из любого состояния класса можно попасть в любое же состояние того же класса.
Класс (эквивалентности) является заключительным, если из состояний данного класса нельзя перейти в состояние, принадлежащее иному классу.
К примеру, все живые схемы (поведения) являются, не зависящими от скорости. Также не зависят от скорости схемы, которые в итоге обязательно останавливаются, причем в единственном состоянии.
Далее автор устанавливает связь между SI схемами с одной стороны, и с полумодулярными, последовательными, дистрибутивными схемами с другой стороны. И в заключение приводит перечень замечательных свойств схем, не зависящих от скорости.

Особенно интересен первый пункт. В нем как раз и говорится о том, что схемы, независящие от скорости, не зависят от задержек логических элементов. К сожалению в тексте не приведены в явном виде основания для данного вывода. Возможно в этом и есть причина последующих недоразумений по поводу термина SI. В действительности же этот вывод совершенно справедлив. В начале 10 главы автором приводятся правила вычисления последующих состояний.

Переход схемы в следующее состояние является следствием переключения выхода какого-то логического элемента (или выходов нескольких элементов). То есть промежуток времени между созданием условий для переключения логического элемента (возбуждением) и самим его переключением ничем не ограничен. А таковой промежуток времени и является задержкой логического элемента. То есть с самого начала автор исходит из предположения, что задержки логических элементов могут быть сколь угодно велики. Действительно, чуть дальше написано следующее.

Ну и, чтоб рассеять все сомнения, цитата с первой страницы 10 главы.

Таким образом установлен непреложный факт: независимость от задержек логических элементов является не свойством схемы, а свойством модели, в которой данная схема исследуется. То есть любая схема, SI или же не SI, исследованная таким же образом, как это описывает Р.Миллер, является не зависящей от задержек логических элементов. В то же время любая схема может быть исследована в модели с ограниченной задержкой. В такой модели множество допустимых состояний является подмножеством множества допустимых состояний при рассмотрении той же схемы в модели с неограниченной задержкой элементов. При исследовании схемы в модели с ограниченной задержкой элементов, схема может быть не зависящей от скорости и в то же время зависеть от задержек элементов.
Таким образом выясняется, что независимость схемы от задержек логических элементов никак не связана со свойством SI. Тогда встает вопрос: а в чем смысл введения определения независимости от скорости? Действительно, рассмотрим две схемы и их поведения.
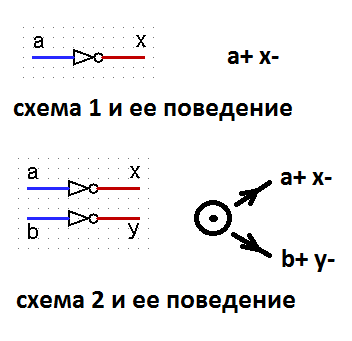
Сигналы a, b для обоих схем входные, сигналы x, y — выходные. Обе схемы реализуют совершенно разумные поведения. Но при этом схема 1 не зависит от скорости, а схема 2 таковым свойством не обладает. Да, можно говорить, что определение SI введено без разделения сигналов на входные и выходные. Но такое разделение сигналов автором подразумевалось, и об этом есть замечание в тексте.
Осмысленность и разумность введения определения свойства SI выявляется только в связи со свойством полумодулярности. Для схем, обладающих свойством полумодулярности, каждый сигнал может снять свое возбуждение не иначе как посредством своего переключения. Не полумодулярные схемы при физической реализации череваты глитчами и метастабильными состояниями. Только полумодулярные схемы могут считаться устойчивыми.
Но связь между свойствами полумодулярности и независимости от скорости односторонняя. То есть полумодулярные схемы не зависят от скорости, но обратное не верно. SI схемы могут быть не полумодулярными. То есть действительно важное свойство, делящее схемы по признаку устойчивости, это полумодулярность. При этом важно понимать, что полумодулярные схемы также могут зависеть от задержек логических элементов, если рассматривать их в модели с ограниченной задержкой.
Но и это еще не все. Свойство полумодулярности также определено для автономных схем, то есть без разделения сигналов на входные и выходные. Из-за этого схемы (поведения) со свободным выбором не отвечают критериям полумодулярности. А между тем эти схемы могут быть такими же устойчивыми, как и полумодулярные. К примеру, вышеприведенная схема 2 не является полумодулярной, но в плане устойчивости она ничем не уступает схеме 1, которая полумодулярной является.
Выход из данного тупика есть. В книге J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev «Logic Synthesis for Asynchronous Controllers and Interfaces» дано определение свойства output persistency (OP).

Именно свойство OP является актуальным свойством, разделяющим схемы (поведения) на устойчивые и не устойчивые. Именно свойство OP должно занять место свойства SI. При этом не следует забывать, что независимость от задержек логических элементов это свойство модели, в которой исследуются схемы (поведения). И OP схемы также могут зависеть от задержек элементов, если рассматриваются в модели с ограниченной задержкой.
Несмотря на всю предыдущую критику, к Р. Миллеру претензий нет. В его работе логических ошибок нет. Вина за более чем полувековое заблуждение лежит скорее на читателях, неверно трактовавших работу Р. Миллера.
Ну и наконец приятный вывод из вышеизложенного. В модель описания поведений STG заложена неограниченная задержка логических элементов. Правила изменения маркировки, извлечения таблицы истинности сформулированы из предположения о неограниченности задержки элементов. Следовательно любая схема, полученная путем вычисления логических функций по STG (либо с помощью таблицы истинности, либо непосредственно по графу), заведомо является не зависящей от задержек логических элементов. Правда надо понимать, что дальнейшие манипуляции с полученной схемой могут привести к потере этого ценного качества.
Комментарии (17)

amartology
30.05.2019 08:57+2У меня очень много вопросов к тому, зачем на Хабре этот узкоспециальный текст, уместный на научном семинаре внутри плотно занимающейся асинхронными схемами научной группы, но задайте начнем с того, что у вас грамматическая ошибка в заголовке)
Для схем, обладающих свойством полумодулярности, каждый сигнал может снять свое возбуждение не иначе как посредством своего переключения
Вы точно этот текст написали для широкой аудитории, а не для двух человек за соседним столом, которые и так в курсе?
Для того, чтобы непосвящённые хоть что-то поняли в ваших сложных взаимоотношениях с Р. Миллером, надо было как минимум объяснить, что такое «асинхронная наука» и для чего она вообще нужна. Сейчас ваш текст выглядит примерно так, что есть, например, физика, есть химия и есть асинхронная наука, а дальше стена из матана, причем не формулами, а скриншотами текста. Ни введения, ни заключения (понятных нормальному человеку), ни рассказа о практической ценности, ни рассказа, причем тут вообще по умолчанию синхронные FPGA.
Akela_wolf
30.05.2019 09:04+1Поддерживаю. Начал продираться через начало статьи, надеясь что дальше пойдет как-то проще, к середине понял что ничего не понял. Язык статьи очень тяжелый, хотелось бы больше наглядных примеров и объяснений «на пальцах»

ajrec Автор
30.05.2019 17:32Ну я же не плачу, что мне не очень понятны статьи о программировании (хотя бы в силу не знакомой терминологии). Вводного курса по программированию я в этих статьях не заметил.

amartology
30.05.2019 18:55Статьи о программировании на сайте о программировании? Или статьи о программировании на сайте о самосинхронных схемах?

ajrec Автор
30.05.2019 17:38Если бы Вы почитали Миллера, то повесились бы.

amartology
30.05.2019 18:58И нет, я бы не повесился, я на самом деле довольно неплохо умею и в математику, и в схемотехнику, и даже в конкретно самосинхронные схемы. Но это все не делает ваш текст лучше и понятнее.

ajrec Автор
31.05.2019 00:06Я не покушаюсь на Ваши достоинства. От чтения Миллера повеситься не зазорно. Если бы Вы задали конструктивный вопрос, я бы с удовольствием ответил. Тем более, что с самосинхронной темой Вы знакомы. То, что моя писанина с первого взгляда не очень понятна, не беда. У меня, действительно, нетрадиционный взгляд на эту проблему. То, что я в меньшинстве, не значит, что я не прав. И свою правоту я могу подтвердить конкретными схемами, которые традиционалистам не доступны.

amartology
31.05.2019 08:56+1Вы знакомы с понятием «диаграмма Венна»? Постройте ее пожалуйста для категорий «целевая аудитория вашего текста» и «аудитория сайта habr.com»
Один и тот же тезис можно изложить по-разному для разных аудиторий. Где-то с места в карьер можно начинать содержательную дискуссию, где-то надо сначала рассказать, кто такой Миллер. Где-то — что такое сасосинхронность. Где-то — как конкретно применить ваш материал для мигания лампочкой на ПЛИС. А кому-то его излагать и вовсе не надо.
Если сейчас выложить на хабр третий параграф четвертой главы произвольной докторской диссертации — его, во-первых, никто не станет читать, во-вторых, заминусуют. И это никак не будет относиться к содержательной части текста, это будет следствием несовпадения ожидаемой и реальной аудитории.

Khort
30.05.2019 09:38Книга Миллера была написана в 70х, когда терия самосинхронных схем только зарождалась, поэтому критиковать ее нет никакого смысла.
Прочитайте лучше последний серьезный учебник на тему самосинхронных схем — Сети Петри Варшавского-Мараховского-Яковлева-Розенблюма, и вот этот учебник уже критикуйте, благо авторы могут ответить на критику
ajrec Автор
30.05.2019 17:27Я так понял, возражения только морально-этического плана. По сути возражений нет? Я бы с удовольствием подискутировал с авторами учебника. Или по крайней мере обменялся мнениями. Если здесь не удобно, я существую на RG (Sergey Bystrov). Но мне кажется, не с руки им до меня снизойти. Кстати об учебнике. В нем нет самого главного: как синтезировать схемы. Туманные намеки на ячейки Давида не впечатляют.
Обижать Миллера цели не было, я уж и так постарался помягче. Просто прочитал, ну никак нельзя было промолчать про казус со SI. Если кто-то уже был в курсе раньше, подскажите — я удалю.
Khort
30.05.2019 17:41В том то и дело, что существует маршрут проектирования полумоделярных схем, котрые, следовательно, являются и самосинхронными. То, что существуют самосинхронные, но при этом — не полумодулярные схемы — известный факт, но ведь для таких схем нет (насколько мне известно) проработанного маршрута проектирования. Таким образом, если самосинхронная схема не изобретается случайно из головы, а проектируется с использованием начальной спецификации и накатанного маршрута, то в 100% случаев она будет полумодулярной.
Касательно авторов учебника по сетям Петри, их почта есть в интернете, в их статьях. И на RG они есть
ajrec Автор
30.05.2019 23:58Вот не поняли Вы меня. Я не покушаюсь на Ваш маршрут. Я только говорю, что Вы приходите на станцию Самосинхронность (независимость от задержек элементов) не потому, что прошли через станцию Полумодулярность, а потому, что, по всей видимости (точного Вашего маршрута я не знаю), Вы с самого начала проложили маршрут в самосинхронном пространстве.
Если есть доказанный вывод: следствием полумодулярности является самосинхронность, подскажите, где его искать. На Миллера уже ссылаться нельзя. Миллер свой анализ делает на основе допустимых последовательностей состояний. Допустимые последовательности он вычисляет, исходя из предположения, что задержка логического элемента не ограничена. То есть изначально Миллер исследует схемы с неограниченной задержкой элементов. Следовательно самосинхронность это не следствие полумодулярности, а изначально принятые правила функционирования схемы. Самосинхронность и полумодулярность свойства пересекающиеся, но не коррелирующиеся. Любую схему можно исследовать как в модели с ограниченной задержкой, так и в модели с неограниченной задержкой. Одна и та же схема может быть полумодулярной в модели с ограниченной задержкой (полумодулярная и не самосинхронная), но не полумодулярной в модели с неограниченной задержкой (не полумодулярная и самосинхронная). Надо правильно лепить ярлыки. Ярлык Самосинхронность надо лепить на модель задержек, в которой схема исследуется. Ярлык Полумодулярность надо лепить на конкретную схему, исследуемую в конкретной модели.
О полумодулярности. Давайте уже употреблять более адекватный аналог — output persistency, тем более, что не я его изобрел. Полумодулярность это подмножество OP. OP ценна уже сама по себе, вне связи с самосинхронностью. На схеме должно стоять два знака качества: OP и самосинхронность. Третий знак касается базиса реализации.
Если, говоря о не проложенном маршруте, Вы имели ввиду не полумодулярные, но OP схемы, не соглашусь с Вами. Маршрут существует, я это уже демонстрировал.
Khort
31.05.2019 00:46Дело в том, что термин полумодулярность — жаргон, применительно к цифровым электрическим схемам. Потому что это математический термин из теории решеток. Началось все с описаний состояний автоматов диаграммами переходов, которые кодировались определенным образом, а потом эти диаграммы подогнали под определения алгебраических структур, операций над ними, и некоторым свойствам. Так из математики были позимствованы термины полумодулярности, дистрибутивности и последовательности, применямые изначально к алгебраическим структурам. Доказательство самосинхронности полумодулярных схем было скорее всего в книге Варшавского 86 года, но наверно есть и в учебнике по сетям Петри. Это доказательство — основание, на котром строится все остальное. Еще ра настоятельно рекомендую почитать этот учебник по сетям Петри, он выложен на RG.
Про маршрут писать не буду, это долго. У меня есть один небольшой пост на эту тему, здесь на хабре.
По поводу Вашего маршрута, должен извиниться, не учел.
Еще могу добавить, что на мой взгляд, при использовании современных тех. процессов все эти модели задержек выглядят уже совершенно оторванными от жизни. А раз так, то единственные действительно не зависящие от любых задержек схемы — т.н. последовательностные (очень узкий подкласс полумодулярных), в которых параллельные процессы не возможны в принципе. На мой взгляд, это серьезный повод забросить эту тему. Для КМОП уже не актуально, а ничего другого на смену пока не пришло.
ajrec Автор
02.06.2019 02:44Обязательно поищу доказательство Варшавского и, если он меня переубедит покаюсь здесь же. Но пока не вижу оснований менять мнение. Анализ на полумодулярность можно провести по двум субстанциям. Схема или поведение. Если это схема, то та же история, что и с Миллером. Если поведение… Для STG наверно рановато, но в любом случае STG модель с неограниченной задержкой и т.д. Диаграмма состояний также модель с неограниченной задержкой. То есть неограниченность задержки заложена в инструмент анализа. Отсюда и все последствия. Понятно, что все это до некоторой степени казуистика: яйцо, курица… Но понимать природу вещей необходимо. В данном случае это не привело к каким-то фатальным провалам. И даже не фатальным. Но вот у того же Миллера есть фраза о том, что последовательностные схемы свободны от состязаний, поскольку нет параллелизма. Дальше тема не развилась и я списал на ошибку перевода. Но по сути уже серьезное заблуждение. Природа состязания лежит не в параллелизме, а в особенностях самих логических элементов. Причем не в физической реализации, а в их модельных свойствах. Пример состязаний для элемента x=NAND(a,b).

В последовательностных поведениях встречается только тип 1. Состязание заключается в том, чтобы событие b- должно восприняться элементом x раньше, чем событие a+. При параллелизме возможные типы поведений 1-7. И везде события b- и a+ не параллельны. Параллелизм никакого отношения к состязаниям не имеет. Последовательностным поведениям состязания также присущи, как и параллельным.
То что задержки проводов приближаются к задержкам элементов, я думаю, не повод для отчаяния. Если использования одних двухвходовых элементов не достаточно, можно пойти дальше: увеличивать расстояние (в событиях) между событиями b- и a+. Причем без ограничений.
Khort
02.06.2019 10:16Я специально качнул этот учебник по сетям Петри, смотрите страницу 206 и ниже. Там связь между решетками, сетями Петри и диаграммами переходов самосинхронных автоматов.
p.s. Варшавский не был соавтором этого учебника, я ошибся.


questor
Зачем половина текста вставлена картинкой, если даже никаких математических символов нет? Текст лучше адаптируется под разные устройства (сотовый/ноутбук), чем картинка.