Более детальная постановка задачи с примерами входа-выхода есть на GeeksForGeeks и LeetCode
Сначала я заметил, что можно легко решить задачу только для горизонтальных или вертикальных линий, складывая X/Y каждой точки в словарь. А чем отличаются остальные линии? Всего лишь наклоном?.. А ведь это поправимо!
Таким образом я решил, что можно несколько раз обходить весь список точек вращая их. И получается решение в O(n)! Хотя и с большим коэффициентом. Очень надеюсь, что я изобрёл не велосипед :)
# *** Константы ***
# Число вращений
# Угол одного вращения = 180/ROT_COUNT градусов
#
# Значение должно быть как минимум 12,
# используйте 180*4 для хороших результатов (6% ошибок),
# и 180*20 для лучших (0% ошибок).
# Бoльшие значения повышают время выполнения.
# Меньшие значения приводят к ложно-отрицательным результатам.
ROT_COUNT = 180*10
# Точность
# Алгоритм полезно рассматривать как поиск максимального числа точек,
# лежащих на полоске с шириной равной 1 / MULT_COEF.
# Подходят значения от 4 и выше.
# Большее значение MULT_COEF требует большего ROT_COUNT.
# Бoльшие значения приводят к ложно-положительным результатам.
# Меньшие значения приводят к ложно-отрицательным результатам.
MULT_COEF = 2 ** 3
angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT)))
def mnp_rotated(points, angle):
"""Returns Maximum Number of Points on the same line with given rotation"""
# Расчёт преобразований
rad = math.radians(angle)
co = math.cos(rad)
si = math.sin(rad)
# Количество точек по разным иксам
counts = {}
for pair in points:
# Расчёт нового икса
nx = pair[0]*co - pair[1]*si
# Для нормального использования словаря нужно целое число,
# а умножение на коэффициент предотвращают
# объединение слишком далёких точек после округления
# и формирует толщину рассматриваемой полоски
nx = int(nx * MULT_COEF)
# Добавляем точку
if nx in counts:
counts[nx] += 1
else:
counts[nx] = 1
# Выбираем наибольшее число
return max(counts.values())
def mnp(points):
"""Returns Maximum Number of Points on the same line"""
res = 0
best_angle = 0
# Простой обход всех нужных углов
for i in angles:
current = mnp_rotated(points, i)
# Сохраняем значение, если оно лучше предыдущего
if current > res:
res = current
best_angle = i
return res
Визуализированно это выглядит примерно так:
моя первая самодельная гифка, просьба не ругать:)
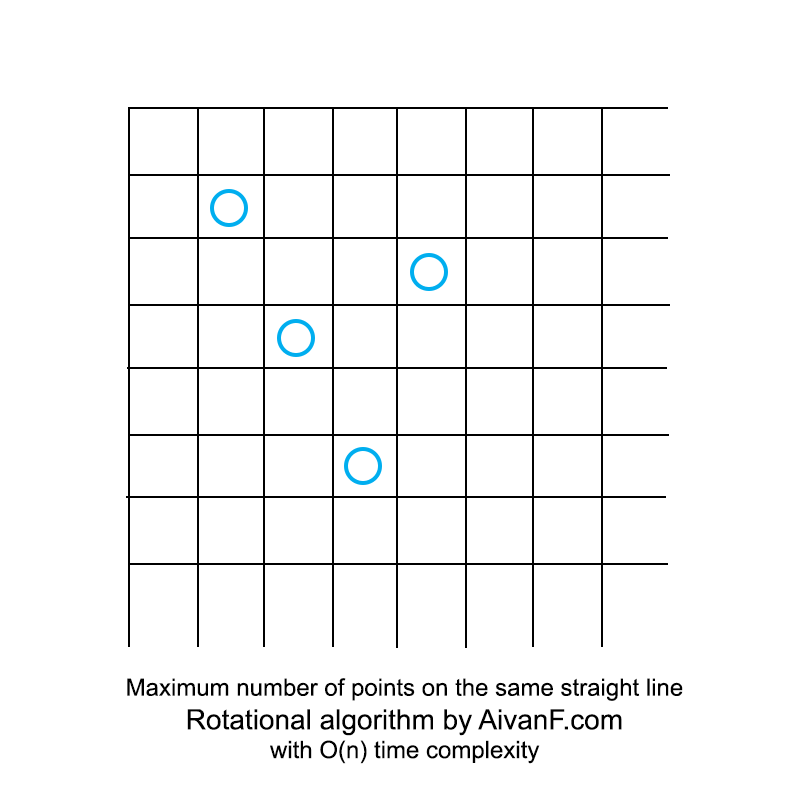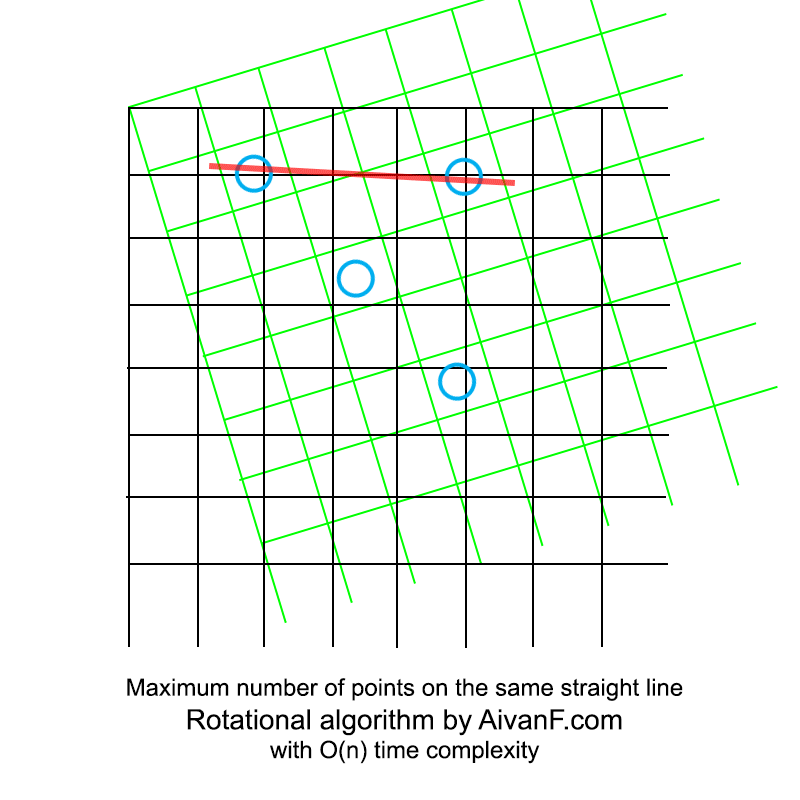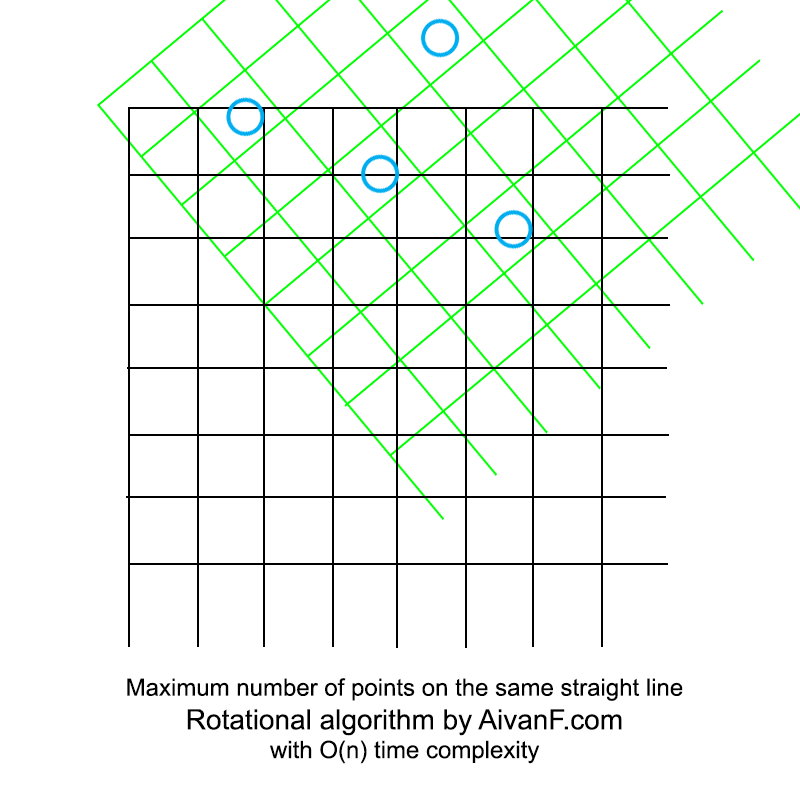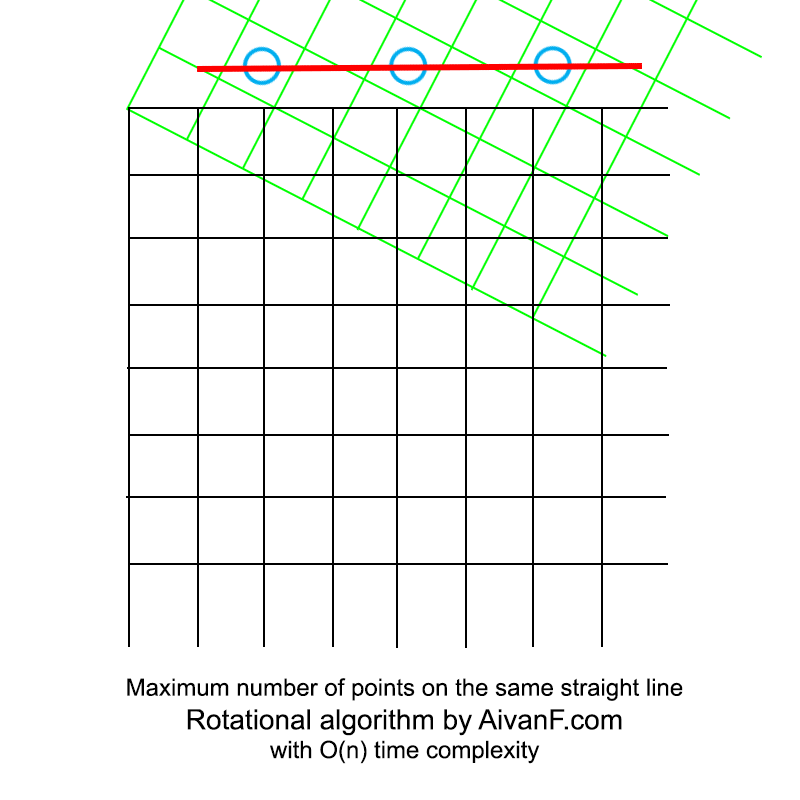
Интересно отметить, что последующая реализация полного перебора заняла больше строк кода.
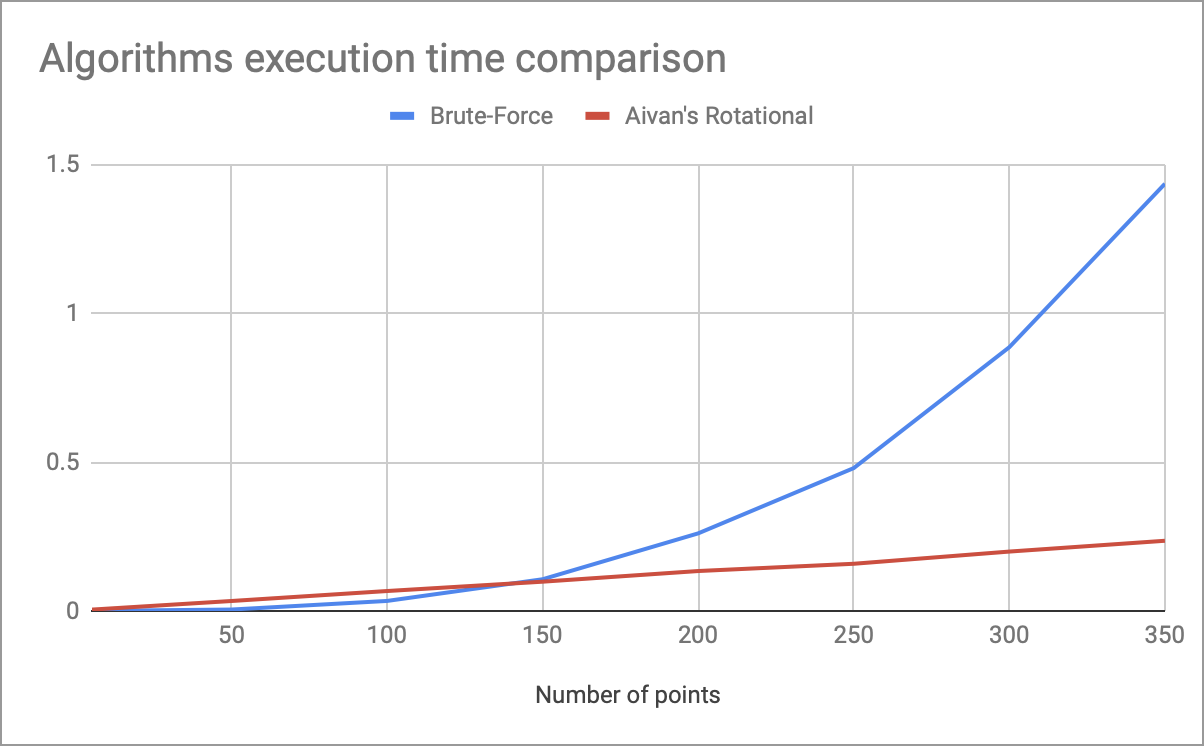
График с замерами времени выполнения моего вращательного алгоритма и полного перебора в зависимости от числа точек есть в шапке.

Примерно на 150 точках проявляется преимущество линейной сложности по времени (при коэффициентах, используемых в коде выше). В итоге, у этого алгоритма есть такие недостатки:
- Точность работы не абсолютная.
- Время выполнения на малых наборах точек велико.
Вообще, это легко исправляется грамотным подбором коэффициентов: для простых наборов вполне достаточно ROT_COUNT = 36, а не 2000, что ускоряет код в 50+ раз.
И такие достоинства:
- Спокойно работает с дробными координатами.
- Временнaя сложность линейна, что заметно на больших наборах данных.
Таблица с измерения доступна здесь. Весь исходный код проекта с обоими алгоритмами и различными проверками есть на ГитХабе.
Update. Хочу ещё раз отметить, что у этого алгоритма есть и преимущества, и недостатки, я его не пропагандирую как идеальную замену брутфорсу, просто описал интересную возможную альтернативу, которая в каких-то случаях может быть более уместна.
Комментарии (53)

DouTro
02.06.2019 05:25Так ведь у вас только вокруг начала координат вращается прямая. А сдвиг? Если точки лежат на прямой скажем y=X+7, то как ее не поворачивай вокруг начала координат, она не совпадет ни с одной прямо проходящей через начало

AivanF Автор
02.06.2019 07:57Так это и не нужно :) Вы кажется неправильно поняли: алгоритм не ищет линии, проходящие через центр, а просто линии, становящиеся при вращении горизонтальными, параллельными оси X (на гифке это вроде видно). Поэтому используется словарь, хранящий множество параллельных линий при каждом вращении (который является хеш-таблицей, поэтому я считал его за О(1)).
Но вообще, я думал о возможной реализации сдвига (например, к среднему всех точек), просто пока всё и без него хорошо работает.

aamonster
02.06.2019 08:31+1Контрпример: возьмём набор точек и умножим им всем x-координату на 1000 (это не изменит набор точек на прямой, но, скорее всего, сделает её почти горизонтальной). Алгоритм сломается: только на шаге с 0 углом он попытается что-то найти — но, скорее всего, не найдёт

AivanF Автор
02.06.2019 08:50Верно подмечено! У моего алгоритма действительно есть трудности с маленькими наклонами из-за чего на случайных сэмплах используется ROT_COUNT около 2000, хотя для простых примеров хватает значений < 50. И если использовать этот алгоритм в продакшне, то без предобработки не обойтись, чтобы масштабировать всю картину согласно распределению точек. И конечно надо быть готовым к неточностям, дробные числа всё же :) Наверное правильнее сказать, что алгоритм ищет максимальное число точек, лежащих на полоске с шириной равной 1 / MULT_COEF.

aamonster
02.06.2019 10:33Для продакшена такие задачи ставятся иначе (обычно точки не обязаны строго лежать на прямой) и, соответственно, есть алгоритмы поинтереснее.
Когда точки на изображении – Hough transform (если ваш алгоритм "вывернуть наизнанку", сделав внешний цикл по точкам, а не по углам – получим нечто похожее)
Для просто набора точек любой размерности – RANSAC.
Ну и прочие.
Но у вас задачка модельная, которую надо решать точно. Тут, судя по целочисленным координатам – даже от деления при проверке, что точки на одной прямой, придётся отказаться (обойтись умножением), или по крайней мере объяснить эти детали.

BorLaze
02.06.2019 14:06+2Вы кажется неправильно поняли: алгоритм не ищет линии, проходящие через центр, а просто линии, становящиеся при вращении горизонтальными, параллельными оси X
# Значение должно быть как минимум 12,
# используйте 180*4 для хороших результатов (6% ошибок),
# и 180*20 для лучших (0% ошибок).
То есть, по сути, утверждается, что при повороте на каждые три угловые минуты мы получим 0% ошибок. Вопрос — откуда вдруг такой вывод?
А если прямая, скажем, наклонена под углом 2.5" — как быть?
В общем случае, очевидно, что сколько бы итераций мы не брали, хоть 180*60, хоть 180*60*60 — всегда можно провести прямую, которая при повороте не будет строго горизонтальной/вертикальной. О чем тогда предложенный алгоритм?
AivanF Автор
02.06.2019 14:09Предложенный алгоритм о том, что есть случаи, с которыми он успешно справляется, а то и лучше классического метода. Да, он не даёт абсолютной точности, но её не дают и многие другие используемые в промышленности алгоритмы – всё зависит от условий конкретной задачи.
Расчёт координат в алгоритме происходит в числах с плавающей запятой, в таких случаях применяют сравнение с погрешностью (то есть, не «x == y», a «y-c < x < y+c»), нечто подобное используется и здесь. Поэтому, как я писал в статье, полезно считать, что алгоритм находит максимальное число точек лежащих на полоске, а не на абсолютно тонкой линии. И ширина этих полосок, как и количество вращений, которыми они «накидываются», задаются теми двумя константами. Поэтому любой угол линии может попасть в эти полосы и успешно обработаться. Но опять же, здесь преимущество в не точности, а в скорости, что может быть полезным в каких-то задачах.
Указанный процент ошибок определялся по случайно сгенерированным набором данных, код генерации которых также есть на ГитХабе.
BorLaze
02.06.2019 14:32+3Собственно, именно это меня и смутило.
Потому как предлагаемое решение никак не решает «классическую задачку для собеседований: поиск максимального числа точек, стоящих на прямой линии» — она решает «поиск максимального числа точек, лежащих в прямоугольнике с заданными сторонами».
Согласитесь, это несколько разные вещи.
AivanF Автор
02.06.2019 14:45"… в прямоугольнике.." – нет, именно на полоске, у которой задаётся толщина, длина же бесконечная, как и у линии. Кажется Вы не очень поняли алгоритм :) После поворота у точек используется лишь одна координата, поэтому длины здесь в принципе нет.
Не могу полностью согласиться, в таких вопросах всегда есть логичные и за, и против. «За» аргументируется тем, что все попавшиеся в интернете примеры этот алгоритм решает успешно, как и крупные случайно сгенерированные сэмплы, притом быстрее стандартного для этой задачи подхода. Да и задачу о поиске линии с мак.числом точек можно сформулировать как поиск полоски с мак.числом точек и минимальной толщиной; с заранее заданными погрешностями, как и во многих программных реализациях идеальней математики.
Аргументы против Вы уже привели, я с ними согласен, но не настолько, чтобы игнорировать аргументы «за». В таких случаях я предпочитаю считать, что конкретное решение может быть уместно в каком-то классе задач. Можно аргументировать и дальше, но вряд ли это будет более плодотворно :)
BorLaze
02.06.2019 15:12Стоп-стоп-стоп…
Может, конечно, я чего-то не понял в объяснениях, но:
допустим, мы после очередного поворота имеем «почти параллельную горизонтали» линию. Скажем, под углом 1".
«Полоска» задана в 1 см, скажем. И на каком-то расстоянии мы честно учтем все точки, как принадлежащие прямой.
Но вот в чем загвоздка — одна угловая минута на расстоянии 100 метров — это чуть меньше трех сантиметров. То есть уже на расстоянии около 30 метров точки прямой выйдут за ширину нашей сантиметровой полоски учета.
Именно поэтому я говорил о прямоугольнике, а не о полосе.
Я в чем-то ошибаюсь?
AivanF Автор
02.06.2019 15:28Понял, Вы имели в виду прямоугольник, который будет построен из точек, а не способ обнаружения самих точек (который всё же полоска бесконечной длины).
Да, всё верно! Может так быть, что на одном шаге полоска на линию из точек ещё не полностью наложится, а на следующем уже пройдёт мимо. Я тоже о таком думал, и была идея реализовать переменный шаг или ещё лучше «отпрыгивание» назад с бинарным поиском между последними двумя вариантами (в моём воображении это очень похоже на градиентный спуск, но с полным проходом, т.к параметр всего один, вращение). В таком случае сложность по времени вырастет (прогнозирую что-то вроде O(n*log(n), а то и квадрат), но и точность станет гораздо больше. Конечно, для рабочей версии этой фичи нужно ещё много продумать – реализовать «умный» выбор, когда производить такой поиск, а когда идти дальше. В общем, это в принципе реализуемо, но нужды пока нет :)
BorLaze
02.06.2019 15:33+1Может так быть, что на одном шаге полоска на линию из точек ещё не полностью наложится, а на следующем уже пройдёт мимо.
Именно!
Я к тому веду, что предложенный алгоритм, может быть, и решает какие-то частные случаи, но в общем, он совершенно не гарантирует правильного решения.
Мы вполне можем иметь цепочку из миллиона точек, лежащих на одной прямой, но из которых в «полоску учета» попала только одна (так уж поворот лег), а вместо нее выберется какой-то совершенно произвольный треугольник, которому повезло уложиться в лимит.
То есть, фактически, мы имеем даже не какую-то погрешность — мы имеем принципиально грубую ошибку.
Что совершенно неприемлемо, чтобы считать алгоритм правильным.

lair
02.06.2019 14:48+1всё зависит от условий конкретной задачи.
Ну, в конкретной задаче подразумевается нахождение точного ответа.
что может быть полезным в каких-то задачах.
В каких, например?

AivanF Автор
02.06.2019 15:01Ну, в конкретной задаче подразумевается нахождение точного ответа.
Вы правы, в конкретно данной задаче это решение не подходит в плане теории. Но на практике успешно справляется со многими входными данными, и было бы полностью подходящим при добавлении допустимой погрешности в условие.
В каких, например?
Честно говоря, я очень глубоко интересовался темой и не знаю, где вообще применяется поиск мак.числа точек на прямой :D Но в математике и алгоритмах временами бывают идеи без очевидного в начале применения, можно считать, что это одно из них. Хотя думаю, что можно легко приспособить этот алгоритм для распознания прямых линий на изображении, но в этой теме решений и без того достаточно.
lair
02.06.2019 15:03+2Но на практике успешно справляется со многими входными данными, и было бы полностью подходящим при добавлении допустимой погрешности в условие.
А "на практике" нет задач, которые нуждаются в этом решении (ну или по крайней мере ни вы, ни я не можем их вспомнить). Вот и получается еще один никому, кроме автора, не нужный кусок кода.

AivanF Автор
02.06.2019 15:14-1Прикол ещё в том, что автору этот кусок кода тоже не нужен! :D Он реально не решает никакой практически полезной задачи и не факт, что будет. Но и эзотерические языки программирования не особо большую практическую ценность несут, они интересны в плане нестандартных идеи. Так и здесь, считайте, что я поделился не алгоритмом, а идеей, как к нему дошёл и реализовал нестандартный способ – приводить наклоненные линии в вертикальные с тривиальным решением.

andy_p
02.06.2019 14:29А что, разве нельзя решить эту задачу за O(n) просто найдя векторное произведение вектора на прямой и вектора точки? Если равно нулю, то точка лежит на прямой.

AivanF Автор
02.06.2019 14:34Вы не так поняли задачу :) Не даётся какая-то конкретная прямая линия, нужно найти максимальное число точек находящихся на любой возможной прямой линии, то есть, попарной комбинации всех точек, поэтому точное решение есть лишь за O(n^2). Я сейчас добавил ссылки с детальным описанием задачи в начало статьи, можете там посмотреть.

shybovycha
02.06.2019 16:56Похожую задачу некогда приходилось исследовать. Насколько я понял постановку задачи для вашего случая, нужно найти прямую, на которой лежит наибольшее количество из заданных точек? (https://en.m.wikipedia.org/wiki/Random_sample_consensus)[RANSAC]. Алгоритм мне, как инженеру, кажется немного бредовым, но там уж требования к алгоритму подтягиваются.

RumataEstora
02.06.2019 16:57Метод наименьших квадратов. Попытка переизобрести?

wataru
01.06.2019 23:32+1Он проведет прямую, на которой не лежит ни одна заданная точка. Но, да, все точки будут в среднем ближе всего именно к этой прямой. Вот только задача — не минимизировать среднюю ошибку, а максимизировать число нулевых ошибок.

pop70
02.06.2019 18:46Если нужно точно, то S=1/2|(x1-x3)(y2-y3)-(y1-y3)(x2-x3)|
Т.е., для каждой пары точек строим треугольники со всеми остальными точками и проверяем площадь на равенство 0. (точнее, на равенство 0 того, что под модулем — оно же определитель матрицы 2х2 из соответствующих разниц координат). Всё в целочисленной арифметике.
Если "с точностью до" (например, ± пол "пикселя"), то вычисляем высоту из этой площади по формуле H=2*S/a, где a — расстояние между парой точек для которых делаем перебор, ну и принимаем решение "попали/не попали". Тут уже с плавающей запятой
lair
02.06.2019 21:32для каждой пары точек
O(N^2).

pop70
02.06.2019 07:24На первый взгляд даже хуже. Ведь, для каждой пары точек (O(N^2)) нужно проверять все остальные точки.
Т.е., О(N^3).
Но зато решается именно исходная задача — точки на прямой, а не в секторе. И точно и целочисленно.
Опять же, усложняя выбор точек, можно некоторые проверки не делать многократно.
Т1, Т2 исключает проверку Т2, Т1.
Найденная тройка (или больше) точек на прямой Та, Тb, Tc… исключает проверку всех других перестановок abc...
AivanF Автор
02.06.2019 09:18Нет, за O(n^2) вполне можно решить если заменить «нужно проверять все остальные точки. Т.е., О(N^3)» на хеш-таблицу и грамотную работу с ней (что составляет O(1)). Посмотрите этот коммент, также этот алгоритм конечно же есть в самом коде, а его замеры в таблице сравнения.

naething
02.06.2019 22:16Довольно странно на питоне замерять время работы.
Можно еще смотреть на идею как на поворот прямой, а не поворот точек. Тогда получается, что вы просто приближаете решение в лоб (которое за O(N^3)): вместо перебора N^2 возможных углов, вы выбираете какое-то фиксированное количество углов. Отсюда можно попытаться найти более «умный» способ построения неравномерной сетки.
naething
02.06.2019 22:18Еще наверняка можно придумать, как к вашему приближенному решению прикрутить идею с хеш-таблицей из решения за O(N^2). Тогда получится сделать сложность O(ROT_COUNT + N) вместо O(ROT_COUNT * N)

mamitko
01.06.2019 23:48Если задача настоящая и точек много, т.е. вычислительная сложность важна, я бы попробовал преобразование Хаффа, а потом какой-нибудь пространственный индекс.
Еще, вместо самодеятельности индексом, можно погуглить, как правильно искать область точек с максимальной густотой.

uchitel
02.06.2019 20:00Я конечно могу ошибаться, но мне почему-то кажется, что эта задача является алгебраической. Ее, вполне, можно свести к матричной форме и копать в сторону ее собственных векторов. Не факт, что это получится быстрее (если получится вообще), наверняка, больше чем O(n^2). Возможно, добиться какого-то ускорения поможет тот факт, что получаемая матрица состоит только из 0 и 1, но опять же — это не факт… почти готов поспорить, что в сингулярном разложении должны присутствовать синусы углов искомых прямых.


daiver19
Ну так вы же не решили задачу, т.к. точность не абсолютная. А если решать честно, то и сложность будет не O(n), а O(n^3), т.к. надо перебрать углы создаваемые всеми парами точек.
Кстати, судя по времени в 1+ сек на 300 точек, вы закодили брутфорс за n^3. Я вроде придумал n^2, но не уверен, что можно быстрее.
AivanF Автор
Примерно такого комментария я и ждал! Если делать точно, то алгоритма быстрее чем O(n^2) действительно не получится – я исследовал тему и где-то нашёл англоязычную статью, которая сводит эту задачу к какой-то более фундаментальной математической задаче о поиске коллинеарных векторов, которая не решается за лучшее время. В итоге, у моего «вращательного» алгоритма есть как недостатки, так и достоинства, которые возможно найдут своё применение :)
Сейчас попробовал аппроксимировать зависимость времени выполнения моего брутфорса, действительно не O(n^2), а что-то ближе к 3! Спасибо за наблюдение :) Очевидно дело в этой строке, которая циклом обходит параллельные векторы. Думаю, что легко можно заменить на работу с ассоциативным массивом (оптимистичный O(1), то есть), надо лишь придумать небольшое преобразование (что есть O(n)), которое приведёт параллельные векторы к одному числу. Сделаю в ближайшее свободное время.
ShadowTheAge
Т.е. вместо одной задачи вы решили другую, зато быстрее?
Могли бы тогда уж и какую-нибудь задачу которая решается за о(1) решить :)
AivanF Автор
Не совсем уместный сарказм :) Посмотрите другие ветки комментов, там это уже обсуждали, что алгоритм успешно справляется с большой частью примеров по данной задаче, а если в условие задачи добавить пару слов о допустимой точности, то он станет полностью уместен. То есть как бы да, решение не совсем по задаче, с другой стороны, это решение не какой-нибудь другой задачи, а весьма близкой и в ряде случаев пересекающейся с этой. Признаю, что я не подумал изначально о таком нюансе т.к привык к практической деятельности, а в ней не часто стоит вопрос абсолютной точности и допустимо рассматривать варианты решения с небольшим проигрышем в точности, но выигрышем по времени.
ShadowTheAge
Все-таки задача «найти что-нибудь точно» и «найти что-нибудь примерно» это совсем разные задачи, и с разными оценками по времени и т.п.
пример — любая NP-полная задача, например задача коммивояжёра. Если кто-то найдет решение такой задачи за полиноминальное время — «нобелевка» (или что там вместо нее в математике) гарантирована. При этом полно полиноминальных алгоритмов, дающих приближенный результат.
Кроме того, не согласен про «большой частью примеров по данной задаче». Если говорить про «большую часть примеров» то в примере будут огромные числа (значения координат), т.к. очевидно что примеров с огромными значениями координат больше чем примеров с маленькими (как на крутящейся гифке в статье). А с огромными числами этот алгоритм не работает никак.
Ну и кроме того не согласен что алгоритм О(n). Это алгоритм от O(n * ROT_COUNT). И говорить что «ROT_COUNT равный 1800 хватит всем» нельзя, не зная задачи. ROT_COUNT в общем зависит от абсолютных значений координат (если координаты в миллиардах, то ROT_COUNT должен быть тоже). И если абсолютные значения координат больше чем n то этот алгоритм хуже чем O(n*n).
AivanF Автор
Действительно получилось добавить то преобразование и довести время полного перебора до O(n^2)! Замеры добавил в Гугл-таблицу. Теперь мой алгоритм проявляет преимущество на более крупных числах, но это в принципе лишь вопрос используемых констант и нужной точности.
Alex_ME
А как за O(N^2)? Я придумал очевидное решение за O(N^3), не обязательно для целочисленных координат, но с точностью до ошибок плавающей запятой.
N^2 прямых, образованных парами точек, для каждой прямой проверяем оставшиеся точки на удовлетворение уравнению прямой.
lair
Проще: вы для каждой пары точек вычисляете уравнение прямой, потом прибавляете единичку в словаре, где ключом являются коэфффициенты этого уравнения. Квадратичная сложность.
AivanF Автор
Да, вкратце именно так. Только вычисления в целых числах не позволят нормально рассчитать параметры уравнения, поэтому смещение и особенно наклон надо считать немного запутанным образом.
lair
Ничего особенно запутанного я пока не вижу.
red75prim
В рациональных числах можно рассчитать без погрешностей и не запутанно.
AivanF Автор
Обратного я не утверждал, моя реализация брут-форса как раз работает без ошибок обрабатывая вместо дробных чисел пары целых. Хотя тема статьи всё же о другом… (:
red75prim
Это я к тому, что обработка "пары целых" "запутанным образом" является расчетом в рациональных числах. Сразу становится яснее что происходит, и можно подумать об использовании модуля fractions.
lair
Поправка: не совсем "прибавляете единичку", там надо сложнее считать число точек. Поторопился. Но на сложность не влияет.
AivanF Автор
Я же на ГитХабе всё выложил :) Вкратце сейчас объясню.
Основная задача – представлять отрезки так, чтобы отличать отрезки на параллельных линиях, но объединять отрезки на одной линии. То есть, надо написать функцию вычисления наклона (get_slope), которая двум отрезкам выдаст одинаковое значение, если они параллельны, а в противном случае разные. И функцию расчёта смещения (get_shift), что даст одинаковое значение для отрезков на одной прямой и разные для параллельных. А дальше просто двойной цикл по всем точкам (т.е, линиям) с записью результатов в словарь вида {наклон: {сдвиг: количество}}. Ну пара мелочей для предотвращения повторений и т.п.