Всем привет! Недавно открыл для себя язык Rust. О своих первых впечатлениях поделился в предыдущей статье. Теперь решил копнуть немного глубже, для этого необходимо что-то посерьёзнее списка. Выбор мой пал на дерево Меркла. В этой статье я хочу:

• рассказать про эту структуру данных
• посмотреть на то, что уже есть в Rust
• предложить свою реализацию
• сравнить производительность

Дерево Меркла

Это относительно простая структура данных, и про неё уже есть много информации в интернете, но думаю, моя статья будет неполной без описания дерева.

В чём проблема

Дерево Меркла было изобретено ещё в 1979 году, но приобрело свою популярность благодаря blockchain. Цепочка блоков в сети имеет очень большой размер (для bitcoin это более 200 ГБ), и далеко не все узлы могут её выкачать. Например, телефоны или кассовые аппараты. Тем не менее им нужно знать о факте включения той или иной транзакции в блок. Для этого был придуман протокол SPV — Simplified Payment Verification.

Как устроено дерево

Это бинарное дерево, листьями которого являются хеши любых объектов. Для построения следующего уровня попарно берутся хеши соседних листьев, конкатенируются и вычисляется хеш от результата конкатенации, что проиллюстрировано на картинке в заголовке. Таким образом, корень дерева представляет собой хеш всех листьев. Если убрать или добавить элемент, то корень изменится.

Как работает дерево

Имея дерево Меркла можно построить доказательство включения транзакции в блок как путь от хеша транзакции до корня. Например, нас интересует транзакция Tx2, для неё доказательством будет (Hash3, Hash01). Этот механизм и используется в SPV. Клиент выкачивает только заголовок блока с его хешем. Имея интересующую транзакцию, он запрашивает доказательство у узла содержащего всю цепочку. Затем делает проверку, для Tx2 это будет:

hash(Hash01, hash(Hash2, Hash3)) = Root Hash

Полученный результат сравнивается с корнем из заголовка блока. Этот подход делает невозможным подделку доказательства, т. к. в этом случае не сойдётся результат проверки с содержимым заголовка.

Какие уже есть реализации

Rust молодой язык, но на нём уже написано много реализаций дерева Меркла. Судя по Github, на данный момент 56, это больше чем на С и С++ вместе взятых. Хотя Go делает их как стоячих с 80 реализациями.

SpinResearch/merkle.rs

Для своего сравнения я выбрал эту имплементацию по количеству звёзд у репозитория.

Это дерево построено самым очевидным способом, т. е. представляет собой граф объектов. Как я уже заметил, такой подход не вполне Rust-friendly. Например, невозможно сделать двунаправленную связь от детей к родителям.

Построение доказательства происходит через поиск в глубину. Если лист с нужным хешем найден, то путь до него и будет результатом.

Что можно улучшить

Делать просто (n+1)-ю реализацию мне было неинтересно, поэтому я подумал об оптимизации. Код моего vector-merkle-tree находится на Github.

Хранение данных

Первое что приходит в голову, это переложить дерево на массив. Это решение будет намного лучше с точки зрения локальности данных: больше попаданий в кеш и лучше предзагрузка. Обход объектов, разбросанных по памяти, занимает больше времени. Удобным фактом является то, что все хеши имеют одинаковую длину, т.к. вычисляются одним алгоритмом. Дерево Меркла в массиве будет выглядеть так:

Доказательство

При инициализации дерева можно создать HashMap с индексами всех листьев. Таким образом, когда листа нет, не нужно обходить всё дерево, а если есть, то можно сразу перейти к нему и подняться до корня, строя доказательство. В своей имплементации я сделал HashMap опциональным.

Конкатенация и хеширование

Казалось бы, что тут можно улучшить? Всё ведь и так понятно — берём два хеша, склеиваем их и вычисляем новый хеш. Но дело в том, что эта функция некоммутативная, т.е. hash(H0, H1) ? hash(H1, H0). Из-за этого при построении доказательства нужно запоминать с какой стороны находится соседний узел. Это делает алгоритм сложнее для реализации, и добавляет необходимость хранить лишние данные. Всё очень легко исправить, достаточно просто отсортировать два узла перед хешированием. Для примера я приводил Tx2, c учётом коммутативности проверка будет выглядеть так:

hash(hash(Hash2, Hash3), Hash01) = Root Hash

Когда не надо заботиться о порядке, алгоритм проверки выглядит как простая свёртка массива:

pub fn validate(&self, proof: &Vec<&[u8]>) -> bool {
    proof[2..].iter()
        .fold(
            get_pair_hash(proof[0], proof[1], self.algo),
            |a, b| get_pair_hash(a.as_ref(), b, self.algo)
        ).as_ref() == self.get_root()
}

Нулевой элемент это хеш искомого объекта, первый — его сосед.

Погнали!

Рассказ был бы неполным без сравнения производительности, которое заняло у меня в несколько раз больше времени, чем реализация самого дерева. Для этих целей я использовал фреймворк criterion. Исходники самих тестов находятся тут. Всё тестирование происходит через интерфейс TreeWrapper, который был реализован для обоих подопытных:

pub trait TreeWrapper<V> {
    fn create(&self,
              c: &mut Criterion, counts: Vec<usize>,
              data: Vec<Vec<V>>, title: String);
    fn find(&self,
            c: &mut Criterion, counts: Vec<usize>,
            data: Vec<Vec<V>>, title: String);
    fn validate(&self,
                c: &mut Criterion, counts: Vec<usize>,
                data: Vec<Vec<V>>, title: String);
}

Оба дерева работают с одной криптографией ring. Тут я не собираюсь сравнивать разные библиотеки. Взял самую распространённую.

В качестве объектов хеширования используются случайно сгенерированные строки. Деревья сравниваются на массивах различной длины: (500, 1000, 1500, 2000, 2500 3000). 2500 — 3000 это примерное число транзакций в блоке биткоина на данный момент.

На всех графиках по оси X — число элементов массива (или количество транзакций в блоке), по Y — среднее время на выполнение операции в микросекундах. Т. е. чем больше, тем хуже.

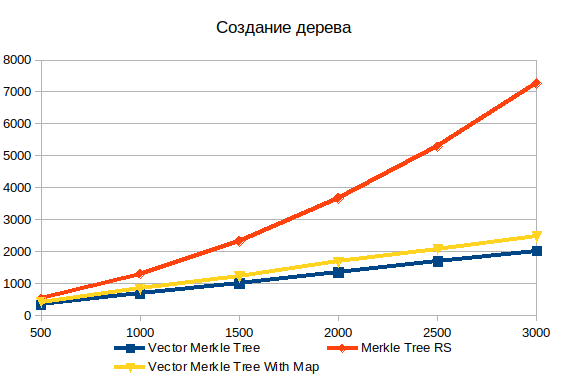
Создание дерева

Хранение всех данных дерева в одном массиве сильно превосходит по производительности граф объектов. Для массива с 500 элементами в 1,5 раза, а для 3000 элементов уже в 3,6 раза. Чётко виден нелинейный характер зависимости сложности от объёма входных данных в стандартной реализации.

Так же в сравнение я добавил два варианта векторного дерева: с HashMap и без него. Заполнение дополнительной структуры данных добавляет где-то 20%, но зато позволяет намного быстрее искать объекты при построении доказательства.

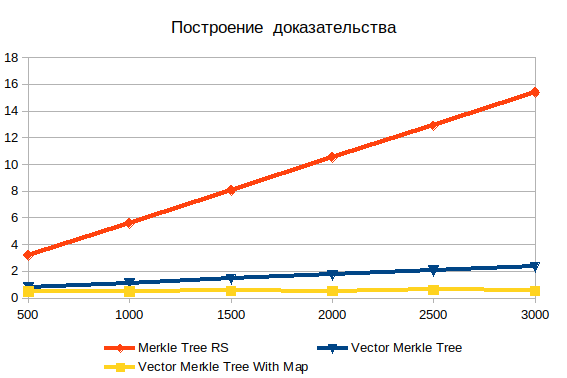
Построение доказательства

Тут видна явная неэффективность поиска в глубину. С увеличением входных данных, она только усугубляется. Важно понимать, что искомыми объектам являются листы, поэтому сложности log(n) быть не может. Если данные предварительно захешированы, то время операции практически не зависит от числа элементов. Без хеширования, сложность растет линейно и заключается в поиске перебором.

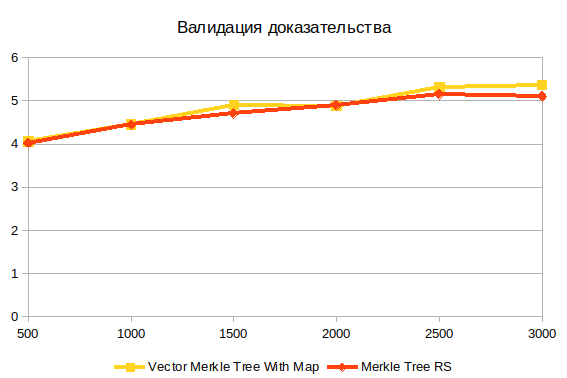
Валидация доказательства

Это последняя операция. Она не зависит от структуры дерева, т.к. работает с результатом построения доказательства. Я полагаю, что основную сложность тут составляет вычисление хеша.

Итог

• Способ хранения данных сильно влияет на производительность. Когда всё в одном массиве — это намного быстрее. И сериализовать такую структуру будет очень просто. Общий объём кода тоже уменьшается.
• Конкатенация узлов с сортировкой сильно упрощает код, но не делает его быстрее.

Немного о Rust

• Понравился фреймворк criterion. Выдает понятные результаты со средними значениями и отклонениями укомплектованные графиками. Умеет сравнивать разные имплементации одного кода.
• Отсутствие наследования не сильно мешает жить.
• Макросы — мощный механизм. Я их использовал в тестах своего дерева для параметризации. Думаю, при плохом их использовании, можно такого натворить, что потом сам не обрадуешься.
• Местами компилятор утомлял своими проверками памяти. Моё первоначальное предположение о том, что так просто начать писать на Rust не получится было верно.
  

Ссылки

• Более полное описание алгоритма работы дерева Меркла
• criterion — фреймворк для нагрузочного тестирования
• merkle.rs — самая популярное дерева под Rust
• vector-merkle-tree — моя реализация дерева
• merkle-tree-test-rs — проект для сравнения производительности двух библиотек