Поисковые подсказки — это здорово. Как часто мы набираем полный адрес сайта в адресной строке? А название товара в интернет-магазине? Для таких коротких запросов обычно хватает ввести несколько символов, если подсказки поиска хороши. И если вы не обладаете двадцатью пальцами или неимоверной скоростью набора текста, то наверняка будете ими пользоваться.
В этой статье мы расскажем о нашем новом сервисе подсказок для поиска по вакансиям hh.ru, который мы сделали в предыдущем выпуске Школы программистов.
У старого сервиса был ряд проблем:

В новом сервисе мы исправили эти недостатки (параллельно добавив новые).
Когда совсем нет подсказок, можно вручную отобрать top-N запросов пользователей и формировать подсказки из этих запросов, используя точное вхождение слов (с учетом порядка или без него). Это неплохой вариант — он прост в реализации, дает хорошую точность подсказок и не испытывает проблем с производительностью. Долгое время наш саджест так и работал, но существенный минус такого подхода — недостаточная полнота выдачи.
Например, в такой список не попал запрос «javascript разработчик», поэтому при вводе «javascript раз» нам нечего показать. Если дополнять запрос, учитывая лишь последнее слово, мы увидим на первом месте «javascript разнорабочий». По той же причине не удастся реализовать исправление ошибок сложнее стандартного подхода с поиском ближайших слов по расстоянию Дамерау-Левенштейна.
Другой подход — научиться оценивать вероятности запросов и для пользовательского запроса генерировать наиболее вероятные продолжения. Для этого используют языковые модели — вероятностное распределение на множестве последовательностей слов.
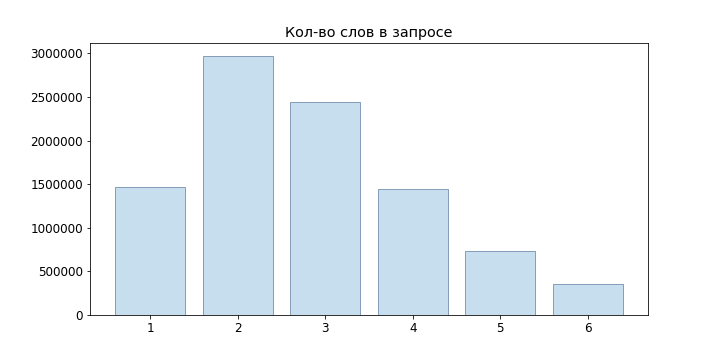
Поскольку запросы пользователей в основном короткие, мы даже не пробовали нейросетевые языковые модели, а ограничились n-граммной:
В качестве простейшей модели можем взять статистическое определение вероятности, тогда
Однако, такая модель не подходит для оценки запросов, которые отсутствовали в нашей выборке: если мы не наблюдали 'junior developer java', то окажется, что
Для решения данной проблемы можно использовать различные модели сглаживания и интерполяции. Мы использовали Backoff:
Где P — сглаженная вероятность (мы использовали сглаживание Лапласа):
где V — наш словарь.
Итак, мы умеем оценивать вероятность конкретного запроса, но как генерировать эти самые запросы? Разумно сделать следующее: пусть пользователь ввел запрос , тогда подходящие нам запросы можно найти из условия
Разумеется, перебирать вариантов и отбирать из них лучшие для каждого входящего запроса не представляется возможным, поэтому используем Beam Search. Для нашей n-граммной языковой модели он сводится к следующему алгоритму:

Здесь узлы, подсвеченные зеленым, — итоговые выбранные варианты, число перед узлом — вероятность , после узла — .
Стало намного лучше, но в generate_candidates необходимо быстро получать N лучших термов для заданного контекста. В случае хранения только вероятностей n-грамм нам необходимо пройти по всему словарю, вычислить вероятности всех возможных фраз, а затем их отсортировать. Очевидно, что для онлайн-запросов такое не взлетит.
Для быстрого получения N лучших по условной вероятности вариантов продолжений фразы мы использовали бор на термах. В узле хранится коэффициент , значение и отсортированный по условной вероятности список термов вместе с . Специальный терм eos обозначает конец фразы.
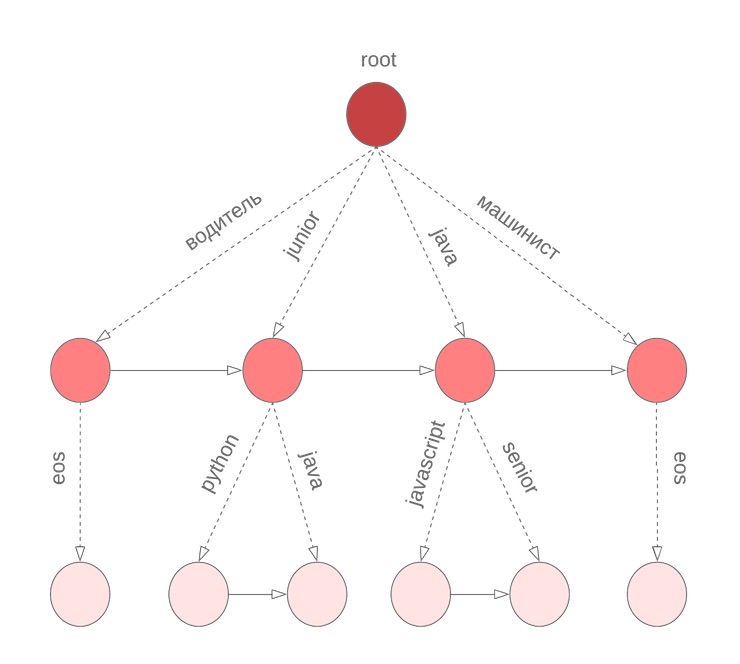
В описанном выше алгоритме мы исходим из того, что в запросе все слова были закончены. Однако, это не верно для последнего слова, которое пользователь вводит его прямо сейчас. Нам снова необходимо пройти по всему словарю, чтобы продолжить текущее вводимое слово. Для решения этой проблемы мы используем посимвольный бор, в узлах которого храним M отсортированных по униграммной вероятности термов. Например, так будет выглядеть наш бор для java, junior, jupyter, javascript при M=3:

Тогда перед началом Beam Search, находим M лучших кандидатов для продолжения текущего слова и отбираем N лучших кандидатов по .
Отлично, мы построили сервис, который позволяет давать неплохие подсказки для пользовательского запроса. Мы даже готовы к появлению новых слов. И все бы хорошо… Но пользовтели опечтыватся и не переключают hfcrkflre клавиатуры.
Как это решить? Первым делом на ум приходит поиск исправлений с помощью нахождения ближайших вариантов по расстоянию Дамерау-Левенштейна, которое определяется как минимальное количество операций вставки/удаления/замены символа или транспозиции двух соседних, необходимых для получения из одной строки другой. К сожалению, данное расстояние не учитывает вероятность той или иной замены. Так, для введенного слова «сапрщик», получим, что варианты «сборщик» и «сварщик» равноценны, хотя интуитивно кажется, что имели в виду второе слово.
Вторая проблема — мы не учитываем контекст, в котором произошла ошибка. Например, в запросе «сапрщик заказов» мы должны все-таки предпочесть вариант «сборщик», а не «сварщик».
Если подойти к задаче исправления опечаток с вероятностной точки зрения, то вполне естественно прийти к модели зашумленного канала:
Затем задача исправления ставится как нахождение правильного слова w для входа s. В зависимости от источника ошибок, мера может строиться по-разному, в нашем случае разумно попробовать оценить вероятность опечаток (назовем их элементарными заменами) , где t, r — символьные n-граммы, а затем оценивать как вероятность получить s из w наиболее вероятными элементарными заменами.
Пусть — разбиение строки x на n подстрок (возможно нулевых). Модель Брилла-Мура предполагает вычисление вероятности следующим образом:
Но нам необходимо найти :
Научившись оценивать P(w|s), мы решим и проблему ранжирования вариантов с одинаковым расстоянием Дамерау-Левенштейна и сможем учитывать контекст при исправлении опечатки.
Для подсчета вероятностей элементарных замен нам вновь помогут пользовательские запросы: составим пары слов (s, w) которые
Для таких пар рассмотрим оптимальное выравнивание по Левенштейну:
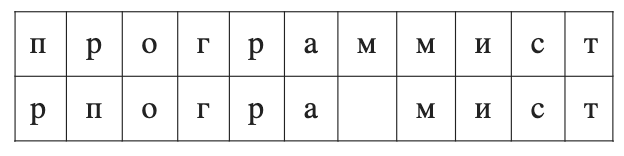
Составим всевозможные разбиения s и w (мы ограничились длинами n=2, 3): п>п, пр>рп, про>рпо, ро>по, м>'', мм>м и т.д. Для каждой n-граммы найдем
Вычисление напрямую занимает : нам нужно перебрать все возможные разбиения w со всеми возможными разбиениями s. Однако, динамикой на префиксе можно получить ответ за , где n — максимальная длина элементарных замен:
Здесь P — вероятность соответствующей строки в k-граммной модели. Если приглядеться, то это очень похоже на алгоритм Вагнера-Фишера с отсечением Укконена. На каждом шаге мы получаем путем перебора всех вариантов исправлений в при условии и выбора из них наиболее вероятного.
Итак, мы умеем вычислять . Теперь нам нужно выбрать несколько вариантов w, максимизирующих . Точнее, для исходного запроса необходимо выбрать такие , где максимальна. К сожалению, честный выбор вариантов не укладывался в наши требования по времени отклика (а срок проекта подходил к концу), поэтому мы решили остановиться на следующем подходе:
Для п.1.2 мы использовали алгоритм FB-Trie (forward and backward trie), основанный на нечетком поиске по прямому и обратному префиксному дереву. Это оказалось быстрее, чем оценивать P(s|w) по всему словарю.
С построением языковой модели все просто: собираем статистику по пользовательским запросам (сколько раз делали запрос данной фразы, какое количество пользователей, какое количество зарегистрированных пользователей), разбиваем запросы на n-граммы и строим боры. Сложнее с моделью ошибок: как минимум, для ее построения необходим словарь правильных слов. Как было сказано выше, для выбора обучающих пар мы использовали предположение, что такие пары должны быть близки по расстоянию Дамерау-Левенштейна, и одно должно встречаться чаще другого в некоторое количество раз.
Но данные все равно слишком шумные: попытки xss-инъекций, неверная раскладка, случайный текст из буфера обмена, опытные пользователи с запросами «программист c not 1c»,запросы от прошедшего по клавиатуре кота.
Поэтому для очистки исходных данных мы исключали:
А также исправляли раскладку клавиатуры, сверялись со словами из текстов вакансий и открытых словарей. Разумеется, всего исправить не удалось, но такие варианты обычно либо совсем отсекаются, либо находятся внизу списка.
Прямо перед защитой проектов запустили сервис в продакшн для внутреннего тестирования, а спустя пару дней — на 20% пользователей. В hh.ru все значимые для пользователей изменения проходят через систему АБ-тестов, что позволяет не только быть уверенным в значимости и качестве изменений, но и находить ошибки.
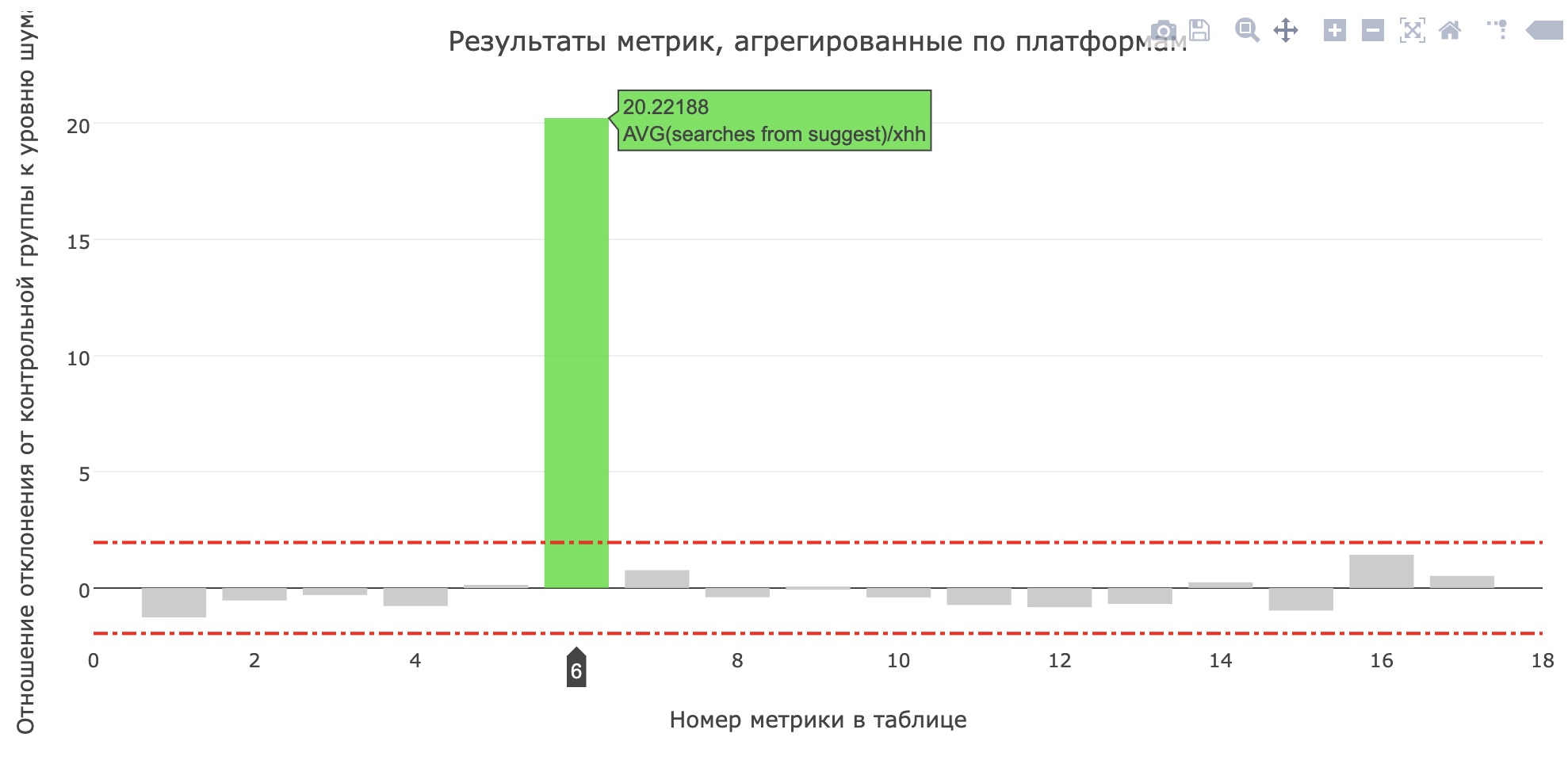
Прокрасилась метрика среднего количества поисков из саджеста на соискателей (увеличилось с 0.959 до 1.1355), а доля поисков из саджеста от всех поисковых запросов увеличилась с 12.78% до 15.04%. К сожалению, основные продуктовые метрики не выросли, но пользователи определенно стали чаще пользоваться подсказками.
В статье не нашлось места для рассказа о процессах Школы, о других опробованных моделях, об инструментах, которые мы написали для сравнений моделей, и о встречах, где решали, какие фичи взять в разработку, чтобы успеть к промежуточным демо. Посмотрите записи прошедшей школы, оставляйте заявку на https://school.hh.ru, выполняйте интересные задачи и приходите учиться. Кстати, сервис для проверки задач также сделали выпускники предыдущего набора.
В этой статье мы расскажем о нашем новом сервисе подсказок для поиска по вакансиям hh.ru, который мы сделали в предыдущем выпуске Школы программистов.
У старого сервиса был ряд проблем:
- он работал на отобранных вручную популярных запросах пользователя;
- не мог адаптироваться под изменение пользовательских предпочтений;
- не умел ранжировать запросы, которые не включены в топ;
- не исправлял опечатки.

В новом сервисе мы исправили эти недостатки (параллельно добавив новые).
Словарь популярных запросов
Когда совсем нет подсказок, можно вручную отобрать top-N запросов пользователей и формировать подсказки из этих запросов, используя точное вхождение слов (с учетом порядка или без него). Это неплохой вариант — он прост в реализации, дает хорошую точность подсказок и не испытывает проблем с производительностью. Долгое время наш саджест так и работал, но существенный минус такого подхода — недостаточная полнота выдачи.
Например, в такой список не попал запрос «javascript разработчик», поэтому при вводе «javascript раз» нам нечего показать. Если дополнять запрос, учитывая лишь последнее слово, мы увидим на первом месте «javascript разнорабочий». По той же причине не удастся реализовать исправление ошибок сложнее стандартного подхода с поиском ближайших слов по расстоянию Дамерау-Левенштейна.
Языковая модель
Другой подход — научиться оценивать вероятности запросов и для пользовательского запроса генерировать наиболее вероятные продолжения. Для этого используют языковые модели — вероятностное распределение на множестве последовательностей слов.

Поскольку запросы пользователей в основном короткие, мы даже не пробовали нейросетевые языковые модели, а ограничились n-граммной:
В качестве простейшей модели можем взять статистическое определение вероятности, тогда
Однако, такая модель не подходит для оценки запросов, которые отсутствовали в нашей выборке: если мы не наблюдали 'junior developer java', то окажется, что
Для решения данной проблемы можно использовать различные модели сглаживания и интерполяции. Мы использовали Backoff:
Где P — сглаженная вероятность (мы использовали сглаживание Лапласа):
где V — наш словарь.
Генерация вариантов
Итак, мы умеем оценивать вероятность конкретного запроса, но как генерировать эти самые запросы? Разумно сделать следующее: пусть пользователь ввел запрос , тогда подходящие нам запросы можно найти из условия
Разумеется, перебирать вариантов и отбирать из них лучшие для каждого входящего запроса не представляется возможным, поэтому используем Beam Search. Для нашей n-граммной языковой модели он сводится к следующему алгоритму:
def beam(initial, vocabulary):
variants = [initial]
for i in range(P):
candidates = []
for variant in variants:
candidates.extends(generate_candidates(variant, vocabulary))
variants = sorted(candidates)[:N]
return candidates
def generate_candidates(variant, vocabulary):
top_terms = []
# сначала отбираем наиболее вероятные термы с контекстом из 1, 2, ... n термов
for n0 in range(n):
top_n = sorted(vocabulary, key=lambda c: P(с|variant[-n0:])
top_terms.extends(top_n)
candidates = [variant + [term] for term in top_terms]
# затем отбираем наиболее вероятные составленные предложения
candidates = sorted(candidates, key=lambda v: P(variant))[:N]
return candidates

Здесь узлы, подсвеченные зеленым, — итоговые выбранные варианты, число перед узлом — вероятность , после узла — .
Стало намного лучше, но в generate_candidates необходимо быстро получать N лучших термов для заданного контекста. В случае хранения только вероятностей n-грамм нам необходимо пройти по всему словарю, вычислить вероятности всех возможных фраз, а затем их отсортировать. Очевидно, что для онлайн-запросов такое не взлетит.
Бор для вероятностей
Для быстрого получения N лучших по условной вероятности вариантов продолжений фразы мы использовали бор на термах. В узле хранится коэффициент , значение и отсортированный по условной вероятности список термов вместе с . Специальный терм eos обозначает конец фразы.

Но есть нюанс
В описанном выше алгоритме мы исходим из того, что в запросе все слова были закончены. Однако, это не верно для последнего слова, которое пользователь вводит его прямо сейчас. Нам снова необходимо пройти по всему словарю, чтобы продолжить текущее вводимое слово. Для решения этой проблемы мы используем посимвольный бор, в узлах которого храним M отсортированных по униграммной вероятности термов. Например, так будет выглядеть наш бор для java, junior, jupyter, javascript при M=3:

Тогда перед началом Beam Search, находим M лучших кандидатов для продолжения текущего слова и отбираем N лучших кандидатов по .
Опечатки
Отлично, мы построили сервис, который позволяет давать неплохие подсказки для пользовательского запроса. Мы даже готовы к появлению новых слов. И все бы хорошо… Но пользовтели опечтыватся и не переключают hfcrkflre клавиатуры.
Как это решить? Первым делом на ум приходит поиск исправлений с помощью нахождения ближайших вариантов по расстоянию Дамерау-Левенштейна, которое определяется как минимальное количество операций вставки/удаления/замены символа или транспозиции двух соседних, необходимых для получения из одной строки другой. К сожалению, данное расстояние не учитывает вероятность той или иной замены. Так, для введенного слова «сапрщик», получим, что варианты «сборщик» и «сварщик» равноценны, хотя интуитивно кажется, что имели в виду второе слово.
Вторая проблема — мы не учитываем контекст, в котором произошла ошибка. Например, в запросе «сапрщик заказов» мы должны все-таки предпочесть вариант «сборщик», а не «сварщик».
Если подойти к задаче исправления опечаток с вероятностной точки зрения, то вполне естественно прийти к модели зашумленного канала:
- задан алфавит ;
- множество всех конечных строк над ним;
- множество строк, являющихся правильными словами ;
- заданы распределения , где .
Затем задача исправления ставится как нахождение правильного слова w для входа s. В зависимости от источника ошибок, мера может строиться по-разному, в нашем случае разумно попробовать оценить вероятность опечаток (назовем их элементарными заменами) , где t, r — символьные n-граммы, а затем оценивать как вероятность получить s из w наиболее вероятными элементарными заменами.
Пусть — разбиение строки x на n подстрок (возможно нулевых). Модель Брилла-Мура предполагает вычисление вероятности следующим образом:
Но нам необходимо найти :
Научившись оценивать P(w|s), мы решим и проблему ранжирования вариантов с одинаковым расстоянием Дамерау-Левенштейна и сможем учитывать контекст при исправлении опечатки.
Вычисление
Для подсчета вероятностей элементарных замен нам вновь помогут пользовательские запросы: составим пары слов (s, w) которые
- близки по Дамерау-Левенштейну;
- одно из слов встречается чаще другого в N раз.
Для таких пар рассмотрим оптимальное выравнивание по Левенштейну:

Составим всевозможные разбиения s и w (мы ограничились длинами n=2, 3): п>п, пр>рп, про>рпо, ро>по, м>'', мм>м и т.д. Для каждой n-граммы найдем
Вычисление
Вычисление напрямую занимает : нам нужно перебрать все возможные разбиения w со всеми возможными разбиениями s. Однако, динамикой на префиксе можно получить ответ за , где n — максимальная длина элементарных замен:
Здесь P — вероятность соответствующей строки в k-граммной модели. Если приглядеться, то это очень похоже на алгоритм Вагнера-Фишера с отсечением Укконена. На каждом шаге мы получаем путем перебора всех вариантов исправлений в при условии и выбора из них наиболее вероятного.
Возвращаемся к
Итак, мы умеем вычислять . Теперь нам нужно выбрать несколько вариантов w, максимизирующих . Точнее, для исходного запроса необходимо выбрать такие , где максимальна. К сожалению, честный выбор вариантов не укладывался в наши требования по времени отклика (а срок проекта подходил к концу), поэтому мы решили остановиться на следующем подходе:
- из исходного запроса получаем несколько вариантов, изменяя k последних слов:
- исправляем раскладку клавиатуры, если у получившегося терма вероятность в несколько раз выше исходного;
- находим слова, расстояние Дамерау-Левенштейна которых не превосходит d;
- выбираем из них top-N вариантов по ;
- передаем на вход BeamSearch вместе с исходным запросом;
- при ранжировании результатов дисконтируем полученные варианты на .
Для п.1.2 мы использовали алгоритм FB-Trie (forward and backward trie), основанный на нечетком поиске по прямому и обратному префиксному дереву. Это оказалось быстрее, чем оценивать P(s|w) по всему словарю.
Статистика запросов
С построением языковой модели все просто: собираем статистику по пользовательским запросам (сколько раз делали запрос данной фразы, какое количество пользователей, какое количество зарегистрированных пользователей), разбиваем запросы на n-граммы и строим боры. Сложнее с моделью ошибок: как минимум, для ее построения необходим словарь правильных слов. Как было сказано выше, для выбора обучающих пар мы использовали предположение, что такие пары должны быть близки по расстоянию Дамерау-Левенштейна, и одно должно встречаться чаще другого в некоторое количество раз.
Но данные все равно слишком шумные: попытки xss-инъекций, неверная раскладка, случайный текст из буфера обмена, опытные пользователи с запросами «программист c not 1c»,
Например, что пытались найти по такому запросу?

Поэтому для очистки исходных данных мы исключали:
- низкочастотные термы;
- содержащие операторы языка запросов;
- обсценную лексику.
А также исправляли раскладку клавиатуры, сверялись со словами из текстов вакансий и открытых словарей. Разумеется, всего исправить не удалось, но такие варианты обычно либо совсем отсекаются, либо находятся внизу списка.
В прод
Прямо перед защитой проектов запустили сервис в продакшн для внутреннего тестирования, а спустя пару дней — на 20% пользователей. В hh.ru все значимые для пользователей изменения проходят через систему АБ-тестов, что позволяет не только быть уверенным в значимости и качестве изменений, но и находить ошибки.

Прокрасилась метрика среднего количества поисков из саджеста на соискателей (увеличилось с 0.959 до 1.1355), а доля поисков из саджеста от всех поисковых запросов увеличилась с 12.78% до 15.04%. К сожалению, основные продуктовые метрики не выросли, но пользователи определенно стали чаще пользоваться подсказками.
Напоследок
В статье не нашлось места для рассказа о процессах Школы, о других опробованных моделях, об инструментах, которые мы написали для сравнений моделей, и о встречах, где решали, какие фичи взять в разработку, чтобы успеть к промежуточным демо. Посмотрите записи прошедшей школы, оставляйте заявку на https://school.hh.ru, выполняйте интересные задачи и приходите учиться. Кстати, сервис для проверки задач также сделали выпускники предыдущего набора.


andreyle
Когда же вы исправите глюк, когда по резюме «Системный администратор» перестанут предлагать вакансии администраторов баров, гостиниц и прочих заведений?
3aBulon
да и не только ) в похожих вакансиях снизу полный бред