В интернете есть много статей с описанием алгоритма градиентного спуска. Здесь будет еще одна.
8 июля 1958 года The New York Times писала: «Психолог показывает эмбрион компьютера, разработанного, чтобы читать и становиться мудрее. Разработанный ВМФ… стоивший 2 миллиона долларов компьютер "704", обучился различать левое и правое после пятидесяти попыток… По утверждению ВМФ, они используют этот принцип, чтобы построить первую мыслящую машину класса "Перцептрон", которая сможет читать и писать; разработку планируется завершить через год, с общей стоимостью $100 000… Ученые предсказывают, что позже Перцептроны смогут распознавать людей и называть их по имени, мгновенно переводить устную и письменную речь с одного языка на другой. Мистер Розенблатт сказал, что в принципе возможно построить "мозги", которые смогут воспроизводить самих себя на конвейере и которые будут осознавать свое собственное существование» (цитата и перевод из книги С. Николенко, «Глубокое обучение, погружение в мир нейронный сетей»).
Ах уж эти журналисты, умеют заинтриговать. Очень интересно разобраться, что на самом деле представляет из себя мыслящая машина класса «Перцептрон».
Двоичная (бинарная) классификация объектов, искусственный нейрон класса «Перцептрон»
Вот наш искусственный нейрон, он делит объекты на два класса (выполняет двоичную классификацию объектов):

Итак, у нас есть:
- На входе: объект выборки — вектор m-мерного пространства
- Весовые коэффициенты по одному на каждый признак объекта выборки (тоже m-мерный вектор)
- Внутри: сумматор — взвешенная сумма входов нейрона
- Дальше: активация
- Еще дальше: квантизатор (порог) — ? [тета]
- Активация+порог — предсказание метки класса объекта по взвешенной сумме входов нейрона (признаков объекта). Эта часть определяет конкретную архитектуру нейрона.
- На выходе: метка класса объекта (одна из двух)
Классификация — потому, что нейрон назначает объекту класс, бинарная (двоичная) — потому, что возможных классов всего два.
[игрек с крышкой] — будем обозначать предсказанное (вычисленное) значение класса для объекта
[обычный игрек без крышки] — истинные (известные) значения класса для объекта из обучающей выборки.
Значения (здесь и дальше и — это не единичные значения, а векторы) меняются от объекта к объекту, весовые коэффициенты (будучи выбраны один раз) остаются неизменны. Для обучающей выборки для каждого объекта известна метка класса . На этапе обучения нужно подобрать весовые коэффициенты так, чтобы модель выдавала правильное значение (совпадающие с ) для максимального количества объектов обучающей выборки. Предположение о полезности обученного таким образом нейрона базируется на надежде на то, что с подобранными коэффициентами он будет выдавать правильные значение для новых объектов , истинное значение класса для которых заранее не известно.
Интуитивный смысл взвешенной суммы входов нейрона заключается в том, что все признаки объекта (каждый из признаков — это один из входов нейрона) оказывают влияние на результат классификации объекта, но не все признаки — в одинаковой степени. В какой именно степени — определяют веса; обнуление какого-то весового коэффициента обнуляет вклад соответствующего признака в общую сумму, т.е. это равносильно удалению у объекта признака.
Адаптивный линейный нейрон ADALINE
Нейрон ADALINE (adaptive linear neuron) — это обычный искусственный нейрон вот с такой функцией активации:
Здесь и дальше верхний индекс в скобках будет обозначать -й элемент обучающей выборки или истинное значение класса или предсказанное значение класса для него же.
Можно сказать, что у такого нейрона функции активации просто нет и на вход квантизатора (порога) подается значение взвешенной суммы входов. Но для единообразия будет удобнее считать, что в качестве активации берется значение взвешенной суммы.
Порог (квантизатор) — предсказывает метку класса:
Если значение активации больше некоторого значения порога ? [тета], то квантизатор назначает объекту метку "1", если значение активации меньше порога ?, то объект получает метку "-1".
Здесь мы можем сформулировать задачу в первом приближении: нам нужно подобрать параметры нейрона
- весовые коэффициенты
- и порог ? [тета]
так, чтобы значения классов , которые нейрон назначает объектам обучающей выборки, совпадали с истинными значениями классов для этих же элементов (или, по крайней мере, давали правильное значение для большинства).
Немного преобразуем пороговую функцию, возьмем случай для класса и перенесем порог в левую часть неравенства:
обозначим и
Как видим, нам удалось избавиться от отдельного параметра ?, внеся его под видом нового весового коэффициента под знак суммы, добавив при этом к описанию объекта новый фиктивный единичный признак .
Скорректируем формулировку задачи с учетом новых обозначений.
Задача': подобрать параметры нейрона — весовые коэффициенты ,
(признак-константа) — фиктивный нейрон (нейрон смещения)
Начиная с этого места нумеруем признаки и весовые коэффициенты c 0, а не с 1. Про вектор будем говорить, как про (m+1)-мерный, а не m-мерный. Вектор в зависимости от контекста можем считать (m+1)-мерным (по большей части в формулах), но при этом помнить, что на самом деле он m-мерный.
Почему нейрон (в нашем случае, правда, это не нейрон, а признак объекта или просто вход, но в случае многослойной сети он превращается в нейрон и обычно его именно так называют) фиктивный — понятно уже сейчас. Почему он еще и смещения станет понятно позднее.
Активация с суммой будут выглядеть теперь так:
Порог теперь всегда 0 (ноль) (реальное значение переехало в параметр ):
Еще раз сформулируем задачу другими словами (геометрический смысл задачи)
Если мы внимательно посмотрим на формулу функции активации, то мы увидим, что она представляется собой параметрическую гиперплоскость в (m+1)-мерном пространстве, при этом в первых m измерениях она сосуществует вместе с точками элементов выборки, а (m+1)-е измерение — пространство значений функции, отдельное от элементов.
Теперь, если мы приравняем значение активации к нулю (значение порога), то это тоже будет гиперплоскость, только уже в m-мерном пространстве, т.е. полностью в пространстве значений элементов . Эта гиперплоскость будет разделять элементы на две непересекающиеся группы.
Обычно в этом месте говорят, что наша задача — подобрать значения параметров , т.е. построить m-мерную гиперплоскость в пространстве элементов так, чтобы элементы обучающей выборки с истинным значением класса "1" оказались по одну сторону плоскости, а элементы с истинным классом "-1" — по другую.
Для тех, кто не совсем понял, что здесь написано, читайте дальше — сейчас мы все увидим, это во-первых. Во-вторых, мы так же увидим, что такая постановка задачи хотя и справедлива, но не совсем полна.
Одномерное пространство (m=1)
Здесь начнет появляться код. Все графики строим с обычной библиотекой Matplotlib, но здесь я еще использую библиотеку Seaborn в одной строчке для настройки области графика, т.к. мне нравится, как у нее это получается, но в принципе можно обойтись и без нее.
# coding=utf-8
import matplotlib.pyplot as plt
import seaborn as sns
# симпатичная сетка на белом фоне
# (без нее русские подписи -> кракозябры)
sns.set(style='whitegrid', font_scale=1.8)
#sns.set(style='whitegrid')
# не будет работать, если включен seaborn
#plt.rcParams.update({'font.size': 16})Берем множество 1-мерных точек и ответов к ним:
import numpy as np
import math
# точки - признаки (одно измерение)
X1 = np.array([1, 2, 6, 8, 10])
# метки классов (правильные ответы)
y = np.array([-1, -1, 1, 1, 1])Здесь у нас каждый i-й элемент массива X1 — это i-й элемент (i-я точка) обучающей выборки (еще точнее — его 1-й и единственный признак): ,
Каждый i-й элемент массива y — правильный ответ, истинная метка, соответствующая i-му элементу обучающей выборки с единственным признаком X1[i].
Возьмем всего 5 точек, первые две отнесем к классу "-1", остальные три — к классу "1".
Нарисуем эти точки на линии:
# ось Ф=0
plt.plot(X1, np.zeros(len(X1)), color='black', lw=2)
# обучающие точки на оси Ф=0
plt.scatter(X1[y==1], np.full(len(X1[y==1]), 0), color='blue', marker='o', s=300,
label=u'объект x (1 признак): класс-1 (y=1)')
plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), 0), color='red', marker='s', s=300,
label=u'объект x (1 признак): класс-2 (y=-1)')
plt.xlabel(u'X1 (единственный признак)')
plt.ylabel(u'Ф (активация)')
plt.legend(loc='upper left')
plt.show()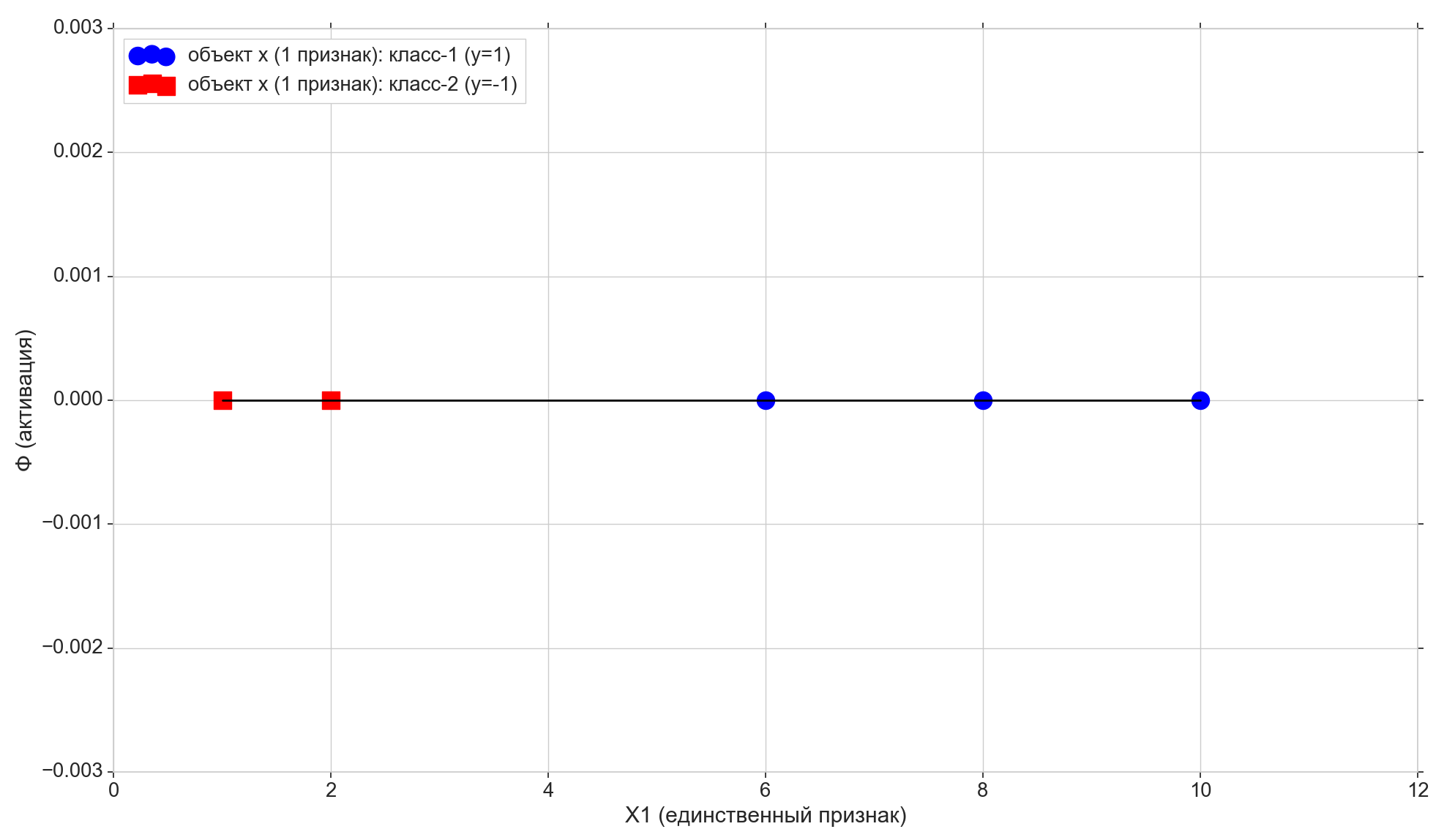
Теперь посмотрим на функцию активации:
Как видим, это обычная параметрическая прямая на плоскости (в 2-мерном, т.е. (m+1)-мерном пространстве):
- на горизонтальной оси у нас лежат точки элементов (они же — значения признака X1)
- на вертикальной — значения активации для каждого элемента
- параметр — задает угол наклона,
- а — сдвиг по вертикальной оси (вот и разгадка к сдвиговому нейрону).
w0 = -1.1
w1 = 0.4
# активация
y_ = w0 + w1*X1
# функция активации (вход для кванзистора - пороговой функции предсказания класса)
plt.plot(X1, y_, color='violet', lw=3,
label=u'активация: w0=%0.2f, w1=%0.2f, sse/2=%0.2f'% (w0, w1, sse/2))
# порог: пересечение активации с Ф=0
plt.scatter([-w0/w1], [0], color='violet', marker='o', s=300, label=u'порог активации')
# проекция обучающих точек на линию активации
plt.scatter(X1[y==1], y_[y==1], color='lightblue', marker='o', s=200,
label=u'активация: класс-1 (y=1)')
plt.scatter(X1[y==-1], y_[y==-1], color='pink', marker='s', s=200,
label=u'активация: класс-2 (y=-1)')
Вспомним еще, что после небольшого преобразования у нас порог активации обратился в ноль. Таким образом, если проекция i-го элемента на линию активации оказывается ниже нуля, мы назначаем элементу класс "-1" (), если выше нуля, назначаем элементу класс "1" ().
Фиолетовая точка — пересечение линии активации с осью , разделяющая элементы из разных классов, — это и есть та самая разделяющая гиперплоскость (для 1-мерного пространства точка — это гиперплоскость), построенная в 1-мерном (т.е. m-мерном) пространстве признаков. Как видим, для того, чтобы разделить элементы на группы, её достаточно, но для того, чтобы назначить группам классы — уже не достатоно. Для того, чтобы назначить элементам классы, нам нужна прямая (2-мерная гиперплоскость) активации, построенная в 2-д (т.е. в (m+1)-д) пространстве «признаки+активация»: направление отклонения активации от вертикальной оси будет определять класс для групп элементов, т.к. от этого зависит, окажутся ли проекции элементов на активацию выше или ниже нуля.
Меняя параметры и мы будем получать разные активационные линии. Нам нужно построить такую линию активации, т.е. найти такую комбинацию параметров , при которой проекция первых двух точек обучающей выборки на линию активации окажется ниже нуля (для них значение ), а проекция оставшихся 3-х точек окажется выше нуля (для них ).
Совершенно очевидно, что в нашем конкретном случае нет ничего сложного в том, чтобы построить такую линию, более того, таких линий вообще можно построить бесконечное количество. Но мы постараемся ее построить так, чтобы удовлетворялся некий критерий оптимальности (может влиять на качество будущих предсказаний), плюс должна быть возможность распространить алгоритм на многомерный случай.
Здесь так же отметим, что мы специально выбрали исходное множество точек так, чтобы его можно было такой линией разделить (для 1-д: все элементы первой группы меньше, все элементы второй группы больше некоторого фиксированного значения), т.е. множество обучающих точек линейно разделимо.
Добавим на график еще две горизонтальные линии, соответствующие классам {1, -1}, и спроецируем на них элементы.
# горизонтальные линии для меток классов (y=1, y=-1)
plt.plot(X1, np.full(len(X1), 1), color='blue', label=u'метка: класс-1 (y=1)')
plt.plot(X1, np.full(len(X1), -1), color='red', label=u'метка: класс-2 (y=-1)')
# обучающие точки на линиях меток классов (y=1, y=-1)
plt.scatter(X1[y==1], np.full(len(X1[y==1]), 1), color='lightblue', marker='o', s=200,
label=u'ответ y: класс-1 (y=1)')
plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), -1), color='pink', marker='s', s=200,
label=u'ответ y: класс-2 (y=-1)')
Точки с классом "-1" проецируем на нижнюю линию , точки с классом "1" проецируем на верхнюю линию .
Обратим здесь внимание на еще один небольшой нюанс. По вертикальной оси мы строим значения активации, пространство значений активации непрерывно. Но результат работы классификатора (функция активации, пропущенная через порог) — дискретное множество из двух элементов {-1, 1}, а не непрерывная шкала. Здесь мы берем дискретное множество классов и накладываем его на непрерывную шкалу активации так, что дискретные значения классов становятся обычными точками на шкале активации — частными случаями значений активации, которые она может непосредственно принимать или приближаться к ним достаточно близко. Строго говоря, мы могли бы изначально в качестве классов взять не числовые значения, а строковые метки "класс-1" и "класс-2", в таком случае мы бы должны были поставить в соответствие строковым меткам числовые значения на шкале активации. Поэтому и в нашем случае значения классов "-1" и "1" следует воспринимать скорее не как метки классов как есть, а как отображение помеченных классов на шкалу активации.
Пришло время ввести метрику ошибки
# линии ошибок - расстояния от точек на линии активации
# до горизонтальных линий меток классов
plt.plot([X1, X1], [y_, y], color='orange', lw=3)#, label='err')
Естественно принять, что чем ближе окажется значение активации для выбранного элемента к значению класса для этого же элемента, тем лучше активация предсказывает для этого элемента его класс. Таким образом, за ошибку для выбранного элемента можно принять расстояние между точками — вертикальной проекцией элемента на линию активации и проекцией элемента на горизонтальную линию его известного (истинного) класса. На графике: ошибки — вертикальные оранжевые линии.
Функция стоимости (потерь)
У нас есть метрика ошибки для каждого отдельного элемента. Мы можем получить из нее метрику качества для всей линии активации. Вполне естественно принять, например, что чем меньше сумма ошибок всех элементов обучающей выборки, тем лучше у нас построена линия активации. Для каждого отдельного элемента ошибка будет не минимальной, но для всей обучающей выборки в целом можно получить некий компромисс.
Но можно взять не простую сумму ошибок, а сумму ошибок, возведенных в квадрат (сумма квадратичных ошибок, sum of squared errors, SSE). Вполне очевидно, что, как и в случае с суммой обычных ошибок, чем ближе линия активации находится к точкам с истинными классами элементов, тем меньше будет и сумма квадратичных ошибок, но в случае с квадратичной ошибкой наиболее удаленные элементы будут получать более серьезный штраф.
На самом деле нас здесь больше интересует не размер штрафа за дальние элементы, а тот факт, что квадратичная функция имеет минимум и при этом везде дифференцируема (у обычной суммы будет минимум, но в этом минимуме она не будет дифференцируема), зачем это нужно, увидим чуть потом.
Итак:
- Ошибка — расстояние от значения метки класса до гиперплоскости активации
- SSE — сумма квадратичных ошибок всех элементов обучающей выборки
- Функция стоимости — метрика качества для выбранной линии активации. Чем меньше значение стоимости, тем лучше активация.
Возьмем в качестве функции стоимости SSE, в общем случае и для линейного нейрона она будет выглядеть так:
( перед SSE, во-первых, не мешает, во-вторых, для удобства — она дальше красиво сократится)
Здесь — номер элемента, а — количество элементов в обучающей выборке. Напомню, что — истинный класс -го элемента обучающей выборки, т.е. заранее известный правильный ответ.
Как мы помним, положение линии активации определяют параметры — весовые коэффициенты , поэтому вектор выступает в качестве параметра функции потерь.
Для 1-мерного случая
Значения и заранее известны (это обучающая выборка), поэтому фиксированы. Мы подбираем параметры , т.е. и так, чтобы значение получилось минимальным. Попробуем построить график, как значение зависит от параметров и
# наиболее удачный по наглядности диапазон
w0 = np.linspace(-10, 10, 200)
w1 = np.linspace(-1, 1, 200)
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.meshgrid.html
# https://stackoverflow.com/questions/36060933/matplotlib-plot-a-plane-and-points-in-3d-simultaneously
ww0, ww1 = np.meshgrid(w0, w1)
sse = []
for j in range(len(w1)):
sse.append([])
for i in range(len(w0)):
sse[j].append(((ww0[j][i]+ww1[j][i]*X1 - y)**2).sum())
sse = np.array(sse)
# https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html
# https://matplotlib.org/api/toolkits/mplot3d.html
from mpl_toolkits.mplot3d import axes3d
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('w0')
ax.set_ylabel('w1')
ax.set_zlabel('J(w)')
#ax.plot_surface(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8)
ax.plot_wireframe(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8,
label='SSE/2')
plt.xlim(-10., 10.)
plt.ylim(-1., 1.)
plt.legend()
plt.show()
В общем, здесь уже видно, что у функции потерь есть минимум, и где он примерно находится. Но давайте сделаем еще один фокус и построим тот же график, только с логарифмической вертикальной шкалой.
#ax.plot_surface(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8)
ax.plot_wireframe(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8,
label='log(SSE/2)')
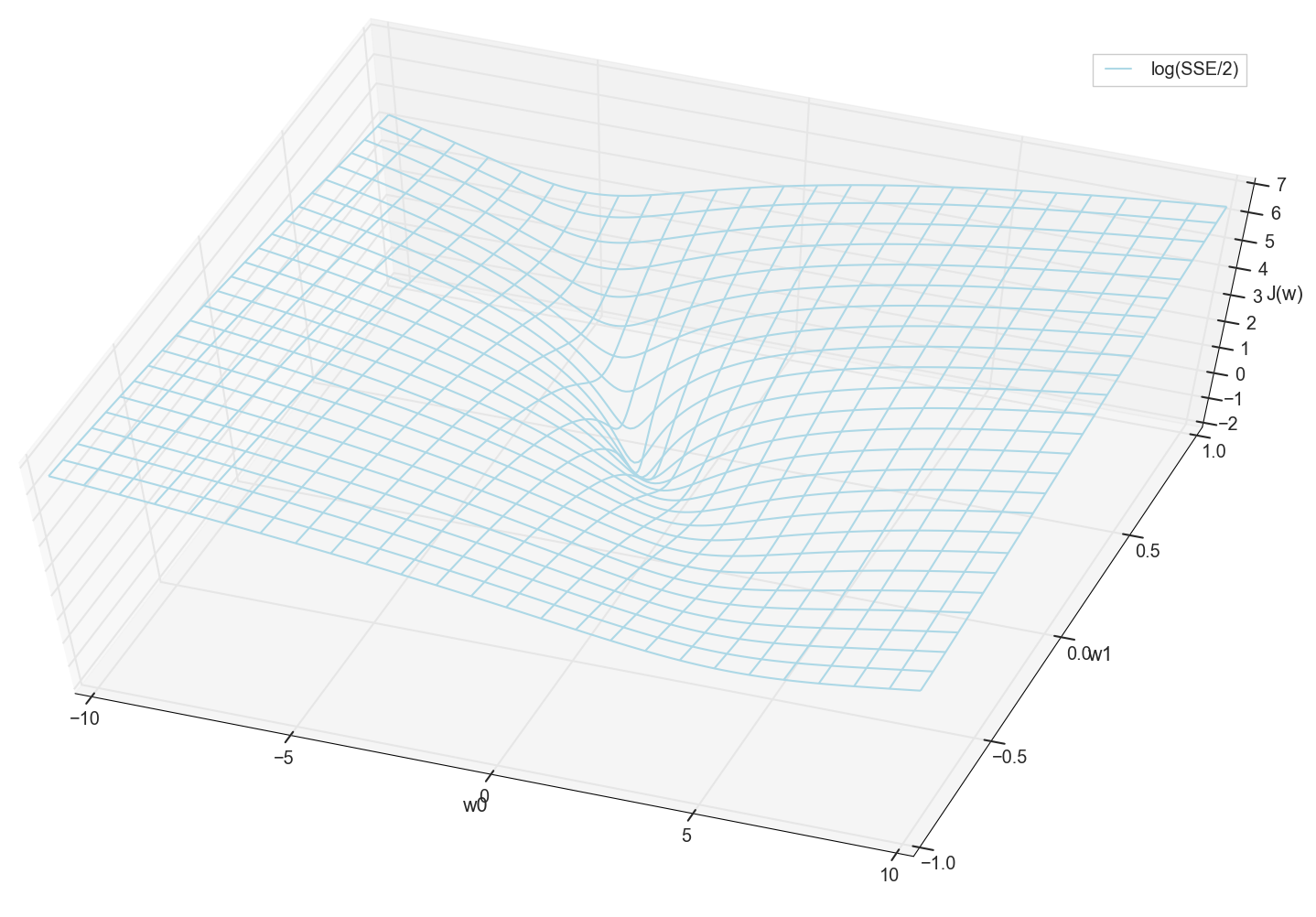
Не знаю, как вы, а лично я, когда увидел этот график в первый раз, испытал просветление. Эта натуральная впадина — не просто образная визуализация многомерных холмов из популярной статьи о нейронных сетях, это реальный график.
Наша задача — подобрать такие значения и , чтобы попасть на дно этой ямы. Получим значения весовых коэффициентов — получим обученный нейрон.
Раз уж мы все равно построили график и воочию наблюдаем его минимум, никто нам не запретит найти его координаты простым перебором на сетке "вручную":
# найдем минимальное значение на сетке
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.min.html
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.amin.html#numpy.amin
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.argmin.html
min_ind = np.unravel_index(np.argmin(sse), sse.shape)
# точка - минимум
#ax.scatter(ww0[min_ind], ww1[min_ind], sse[min_ind]/2, color='red', marker='o', s=100,
ax.scatter(ww0[min_ind], ww1[min_ind], math.log(sse[min_ind]/2),
color='red', marker='o', s=100,
label='min: w0=%0.2f, w1=%0.2f, SSE/2=%0.2f' % (ww0[min_ind], ww1[min_ind], sse[min_ind]/2))
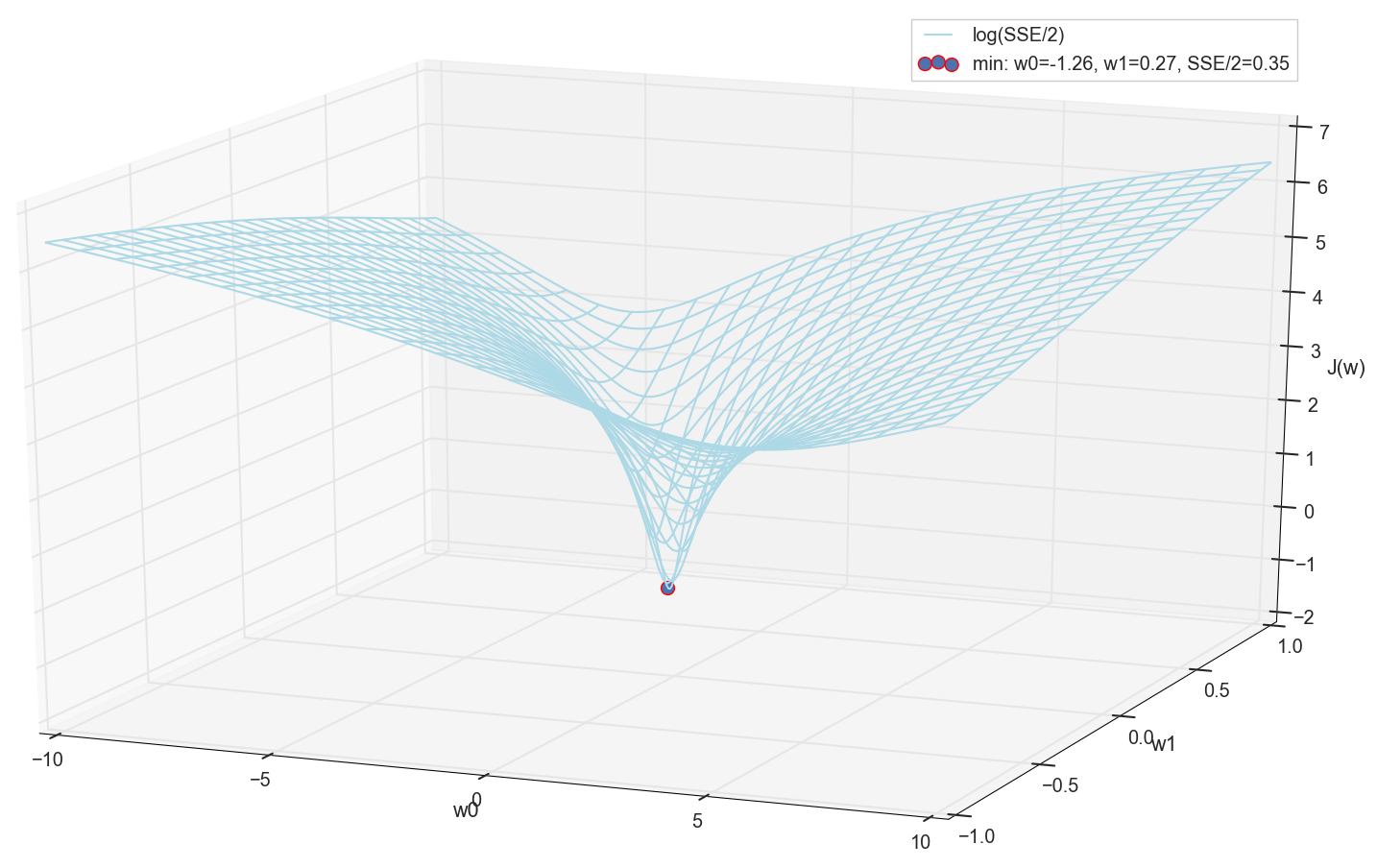
Это значения: и , сумма квадратичных ошибок SSE при этом 0.69, функция стоимости (более точно: 0.3456478371758288).
Посмотрим, как с этими параметрами выглядит активация:
# оптимум "вручную" по сетке (SSE=0.69, sse/2=0.345)
w0 = -1.26
w1 = 0.27
Как по мне, вполне норм. Точка пересечения активации с нулевым порогом разделяет элементы из разных классов, а сама активация назначает им правильные значения. При этом активация, похоже, находится в некотором оптимальном положении.
Перед тем, как двигаться дальше, еще раз полюбуемся на график на сетке пошире:
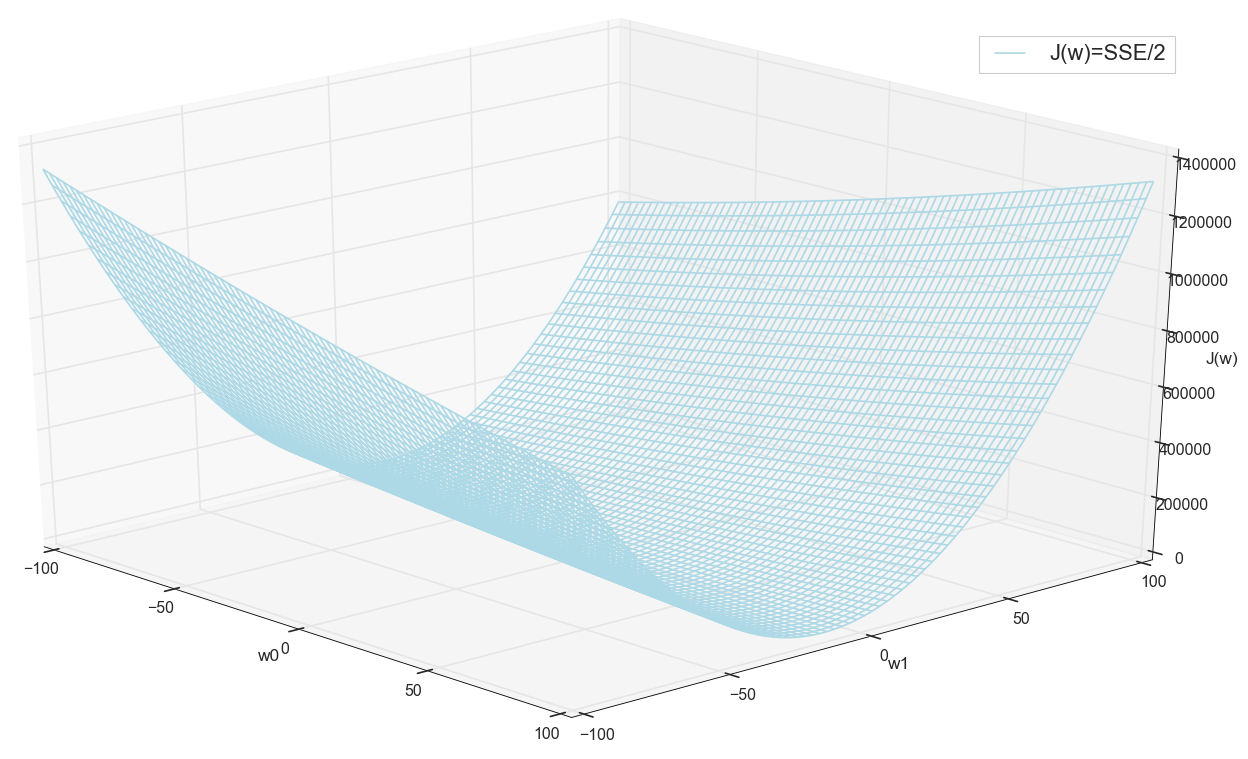
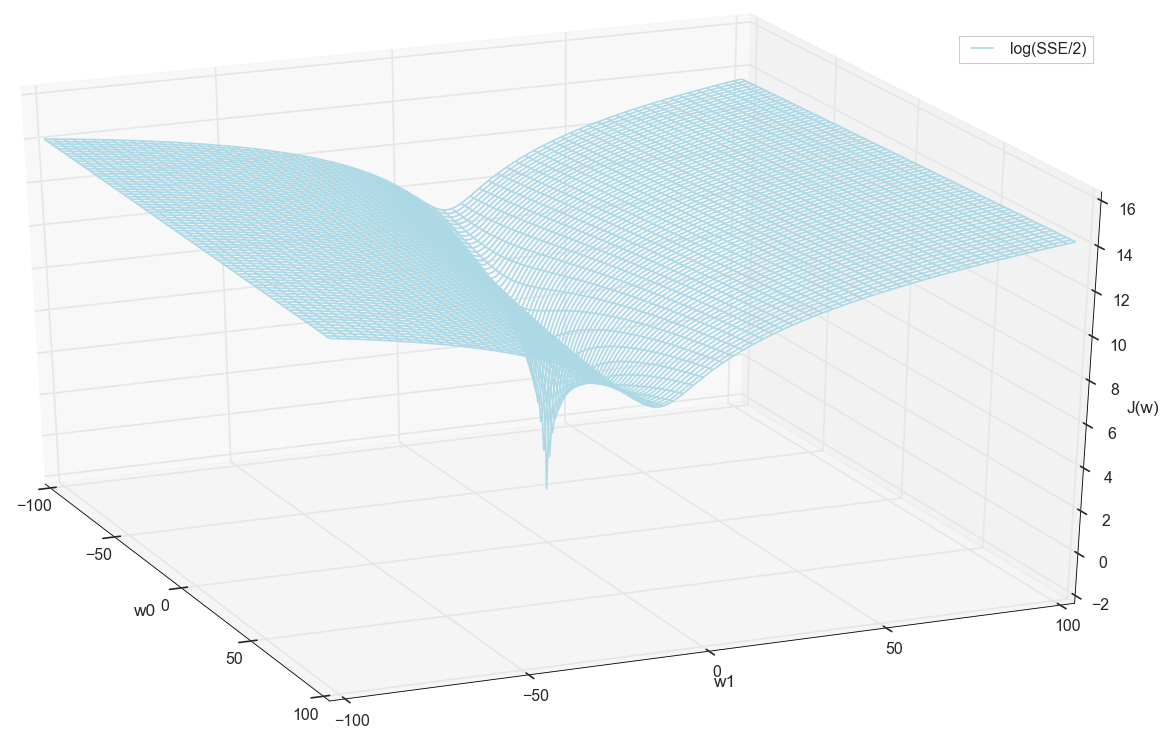
Похоже, что никаких других минимумов поблизости нет, кто бы мог подумать.
Поиск минимума
Итак, мы получили весовые коэффициенты — координаты минимального значения ошибки. Это будет оптимальное значение весовых коэффициентов на обучающей выборке. Вообще говоря, именно это нам и нужно, можно сказать, что нейрон обучен. Может на этом можно и завершить?
Поиск минимума: перебор по сетке
- Вариант на первый взгляд вполне рабочий (как видим)
- Нужно заранее знать область, где искать минимум (можно взять достаточно большие границы, затем сужать область поиска — это только на глаз)
- Для повышения точности нужно уменьшать шаг > еще больше точек (решение: можно итеративно сужать область поиска)
- Слишком много точек (для 2д может и ок, но для многомерных случаев очень быстро упремся в ресурсы)
- Для MNIST (28x28=784 пикселей — столько же входов, весовых коэффициентов столько же плюс смещение, сетка 100 шагов на размерность): 100^785=10^1570.
Значит, если мы захотим обучить один-единственный нейрон (даже не нейросетку) на изображении 28x28=784 пикселей методом поиска минимума прямым перебором на сетке в 100 точек на каждое измерение, нам нужно перебрать 10^1570 комбинаций. Это довольно много и для хранения, и для перебора (в видимой части Вселенной всего 10^80 атомов, Вселенная существует примерно 4*10^17 секунд = 4*10^26 наносекунд).
Попробуем найти вариант побыстрее.
Поиск минимума: спуск с постоянным шагом
Посмотрим на график функции потерь на плоскости: фиксируем , меняем
def sse_(X, y, w0, w1):
return ((w0+w1*X - y)**2).sum()
# фиксируем w0, строим график J(w1)=sse(w1)/2
w1 = np.linspace(-1, 1, 200)
sse = [[], [], []]
for i in range(len(w1)):
sse[0].append(sse_(X1, y, -1, w1[i]))
sse[1].append(sse_(X1, y, 0, w1[i]))
sse[2].append(sse_(X1, y, 1, w1[i]))
sse = np.array(sse)
plt.plot(w1, sse[0]/2, color='orange', label='w0=-1')
plt.plot(w1, sse[1]/2, color='blue', label='w0=0')
plt.plot(w1, sse[2]/2, color='red', label='w0=1')
plt.xlabel('w1')
plt.ylabel('J(w)')
plt.legend()
plt.show()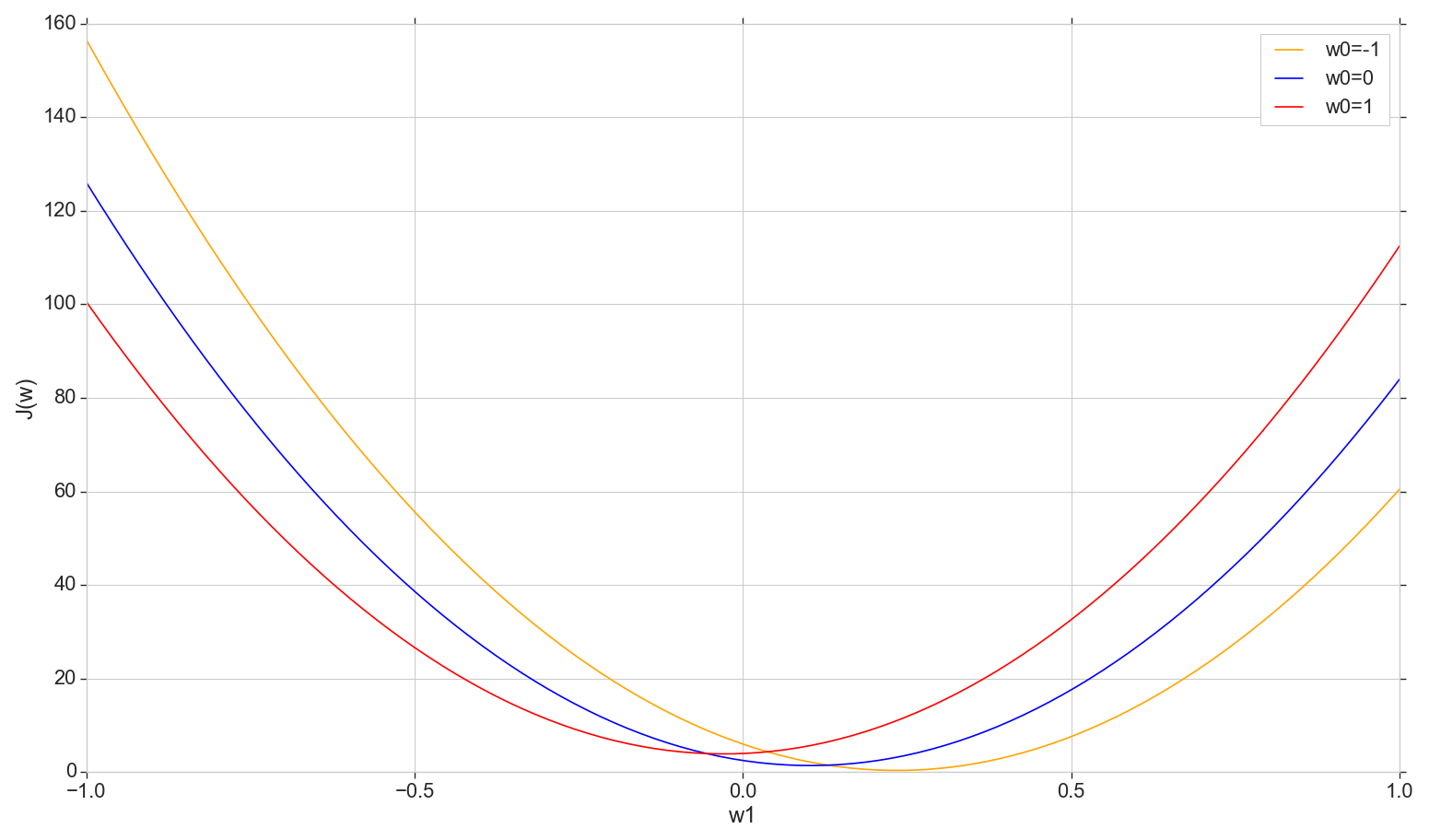
Это обычная парабола (точнее, семейство парабол — они будут немного отличаться в зависимости от того, какое именно значение зафиксировали на ). Чтобы найти минимум параболы, не обязательно перебирать все точки. Мы можем выбрать произвольную точку на горизонтальной оси и двигаться в сторону минимума с некоторым шагом.
Рассмотрим вариант с постоянным шагом
- Если шаг слишком большой, можно промахнуться, так и не подступившись к минимуму (шаг можно уменьшить)
- Если слишком маленький, будет слишком много шагов (больше, чем могло бы быть)
- Точный минимум мы в любом случае не достигнем, но можем достигнуть с произвольной точностью, поменяв около найденного неточного минимума шаг (шаг перестает быть постоянным)
- Не знаем направление спуска (можно решить алгоритмически: не шагать в сторону увеличения ошибки)
- Проблема с поиском диапазона решена (можно спускаться из любой точки — рано или поздно все равно спустимся вниз)
- В принципе, вариант рабочий, но может есть вариант получше?
Замечание: когда я рассказывал про такой вариант спуска на лекции, один студент спросил, зачем нужно двигаться по шагам, если можно сразу найти минимум параболы по формуле? Я сначала ответил что-то в духе, что нам сейчас интересно рассмотреть вариант с итерациями, чтобы потом иметь возможность применить его не только с параболой, но и в других ситуациях. Плюс к этому, на самом деле нам не нужен минимум параболы конкретно на этом срезе — мы будем двигаться к минимуму не по одному измерению, а по всем измерениям поочередно так, что на каждой новой итерации новый шаг будет проходить не по этой параболе, а на параболе с нового среза со сдвинутым значением . Но подумав позднее, я подумал, что в принципе нет ничего плохого, если мы на каждом срезе будем двигаться не шагами, а скатываться сразу к минимуму текущего среза. Так раз за разом измерение за измерением мы должны все равно скатиться к глобальному минимуму, и, похоже, быстрее, чем по шагам. Для единственного нейрона должно сработать, и не только с параболой. Но я пока не стал тратить время на проверку этой теории, поэтому здесь просто двинемся дальше — я обещал рассказать про градиентный спуск.
Поиск минимума: градиентный спуск
В общем так, спускаемся по шагам, но делаем это более умно. Используем для подбора шага производную кривой стоимости (здесь не кривая стоимость, а кривая стоимости).
- У нас несколько измерений и в каждом из них своя кривая: фиксируем все , кроме ,
- будет кривая ошибки в -ом измерении
- Все они — (в нашем случае) параболы, но, вообще говоря, важно только то, что они везде дифференцируемы и имеют минимум
- Для регулировки шага в каждом измерении будем использовать частную производную функции ошибки по этому измерению (изменяющемуся коэффициенту ).
- Вектор из таких частных производных называется градиент
Это всё хорошо, но причем здесь производная? Сейчас разберемся.
Геометрический смысл производной
Для меня производная долгое время оставалась набором специальных формул и правил для ее вычисления, плюс что-то про возрастание, убывание и экстремумы. Здесь будет уместно вспомнить или выяснить, что из себя представляет производная на самом деле.
Производная функции в данной точке — это предел отношения приращения функции к приращению аргумента при приращении аргумента , стремящемся к нулю:

На картинке точка — точка, в которой мы хотим определить производную. Точка — точка, получаемая приращением аргумента . Прямая — секущая, проходящая через эти две точки.
Точка — пересечение секущей с горизонтальной осью .
Рассмотрим два прямоугольных треугольника: треугольник с участком секущей в качестве гипотенузы и треугольник с продолжением секущей до оси — отрезком в качестве гипотенузы. Из графика и школьного курса геометрии очевидно, что углы и равны, а значит равны и их тангенсы:
Добавим на картинку: — касательная к исходной кривой в точке , пересекает ось в точке . Треугольник — прямоугольный треугольник с гипотенузой — участком касетельной, отрезком .
Устремляем приращение к нулю:
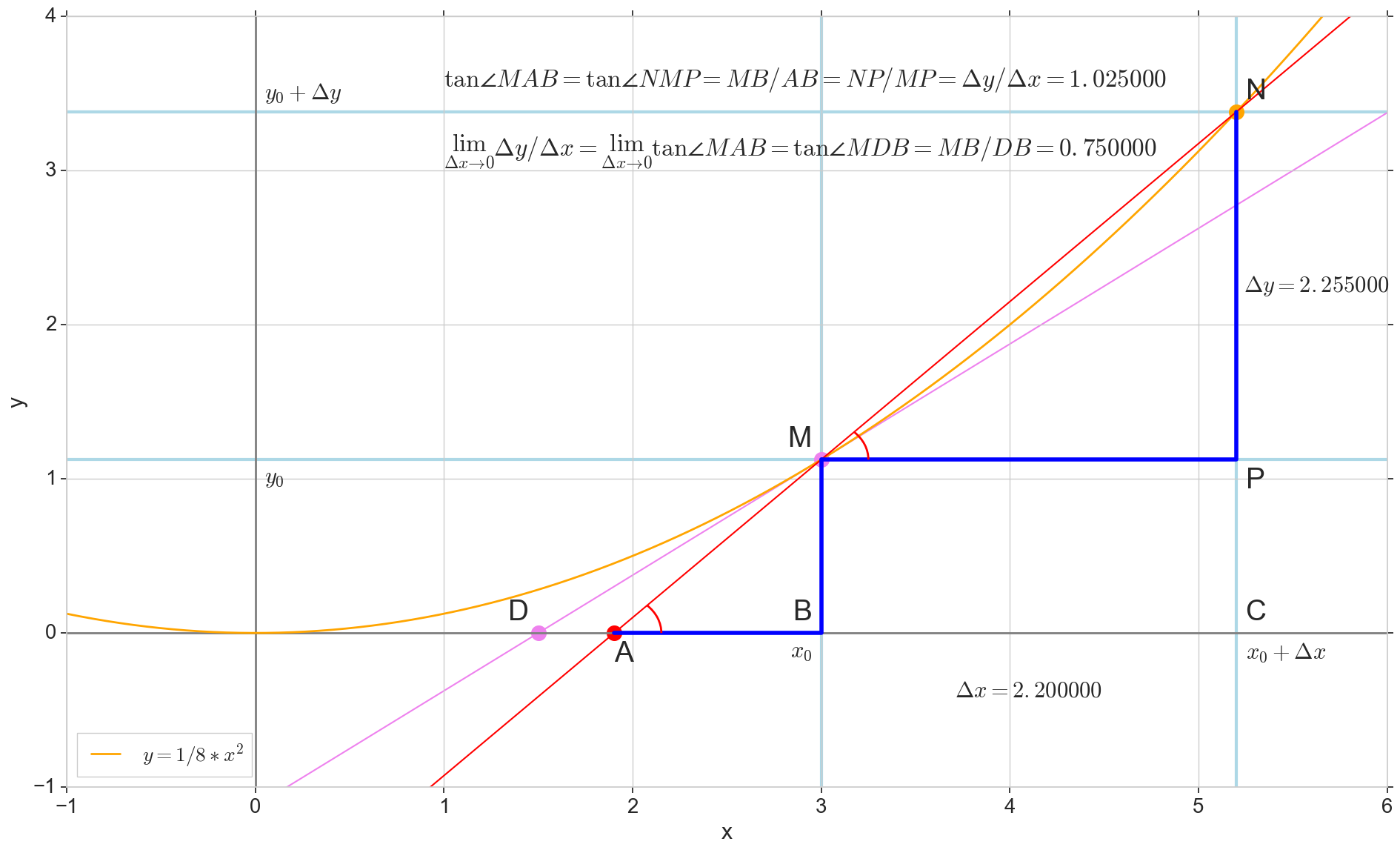
Точка съезжает в точку по функции, точка ползет в точку по оси , секущая превращается в касательную с точкой касания . Исходный треугольник с катетами и сжимается в точку, но подобный ему треугольник превращается в треугольник , сохраняя не только макроскопические габариты, но и равенство углов и .
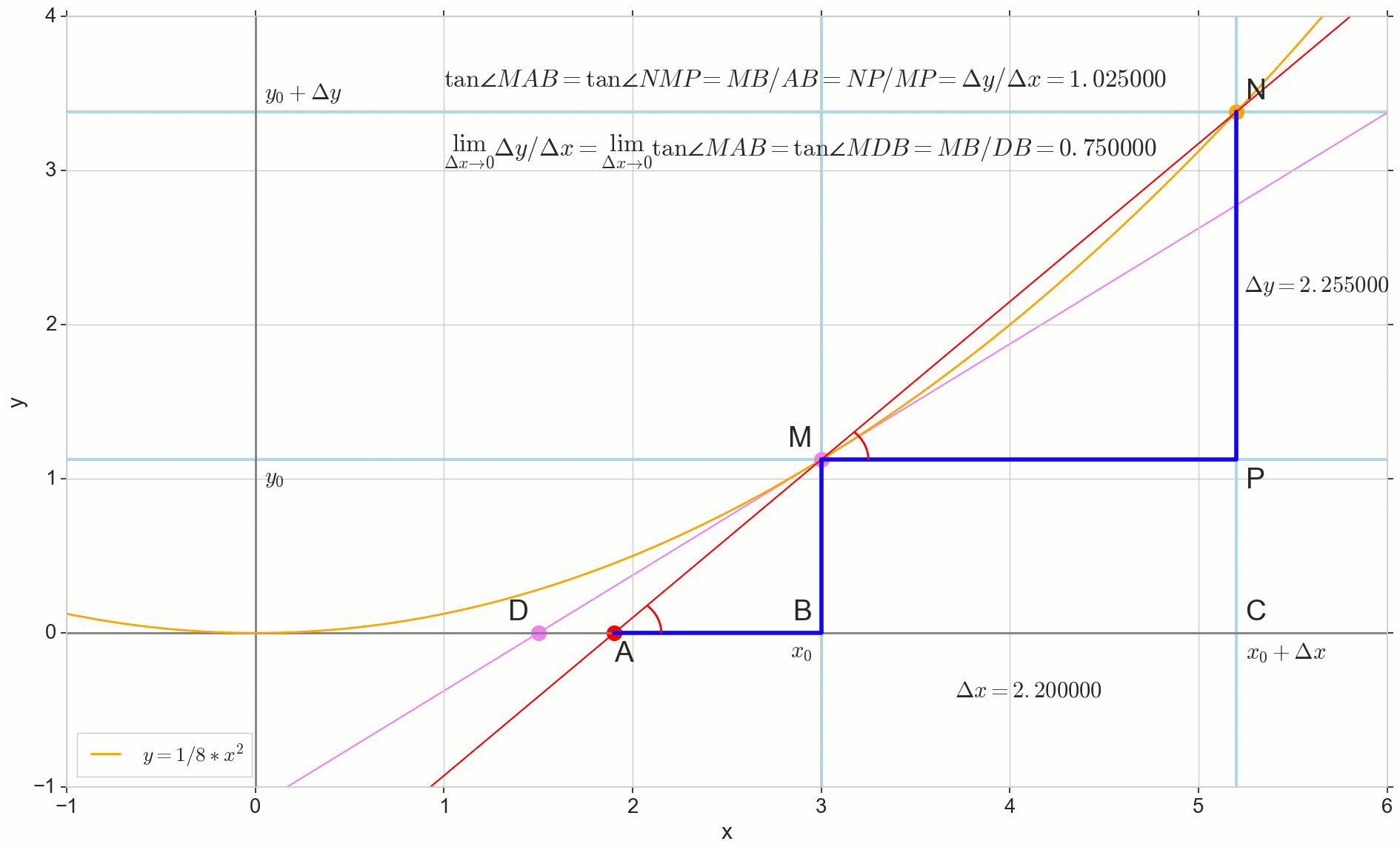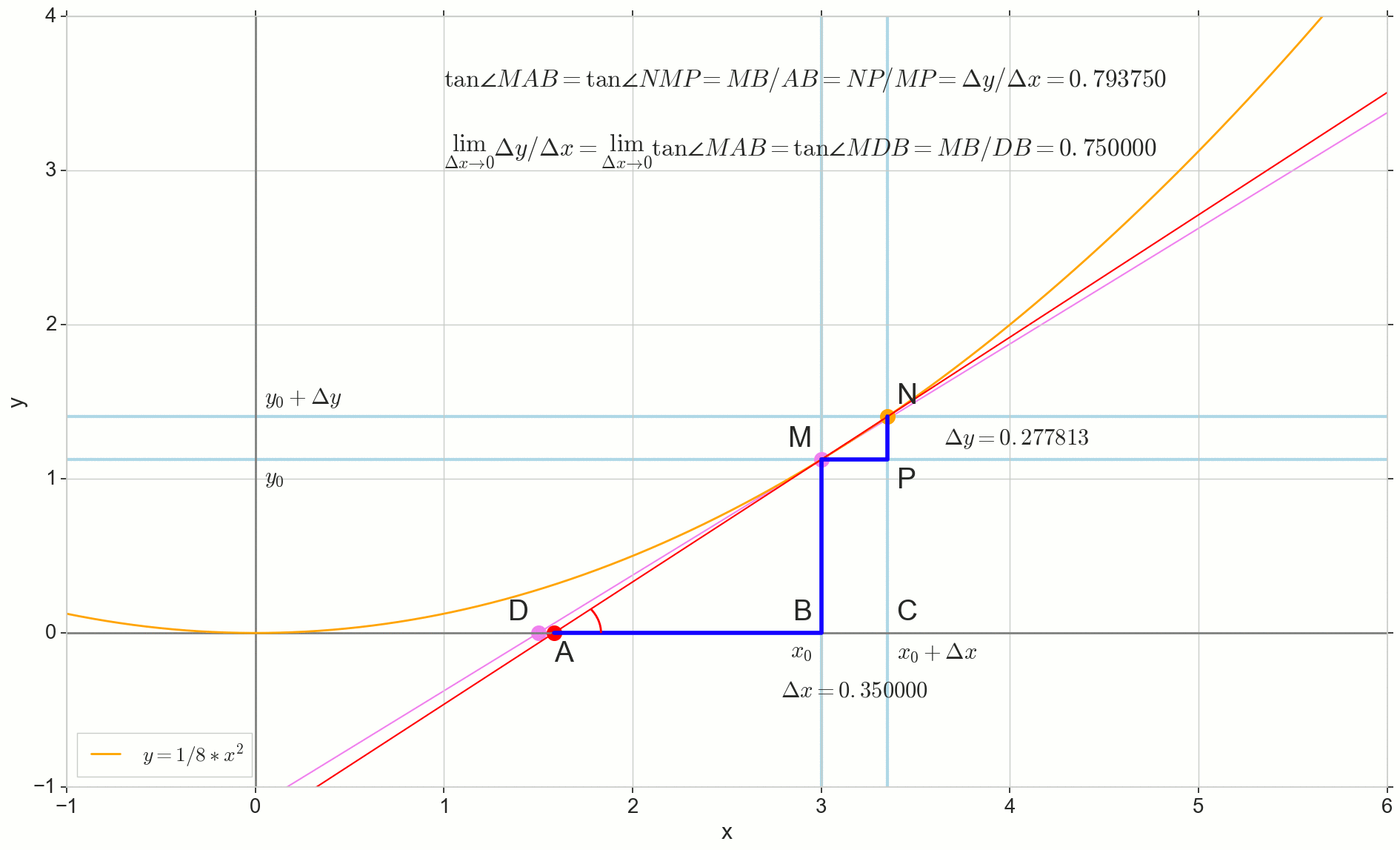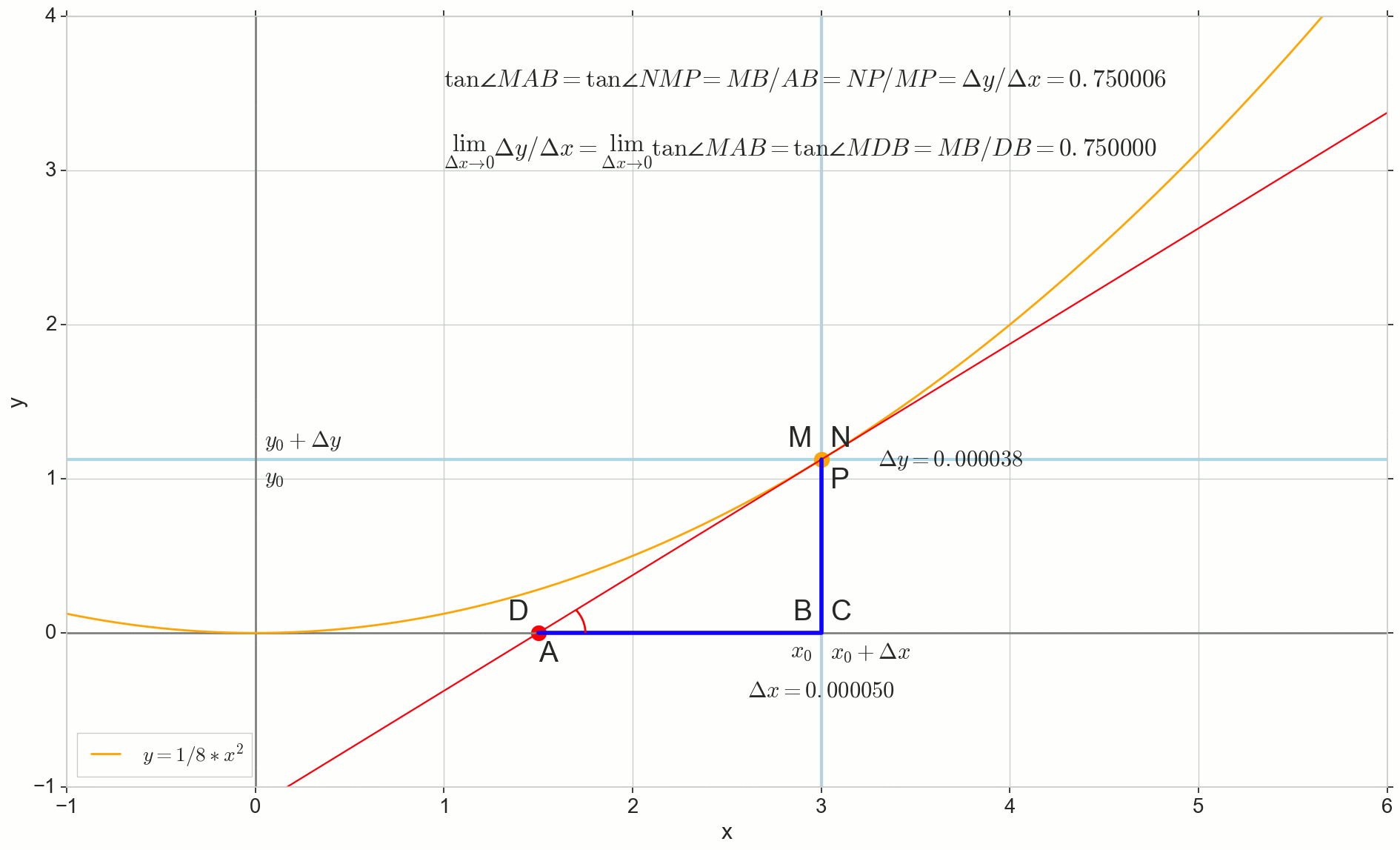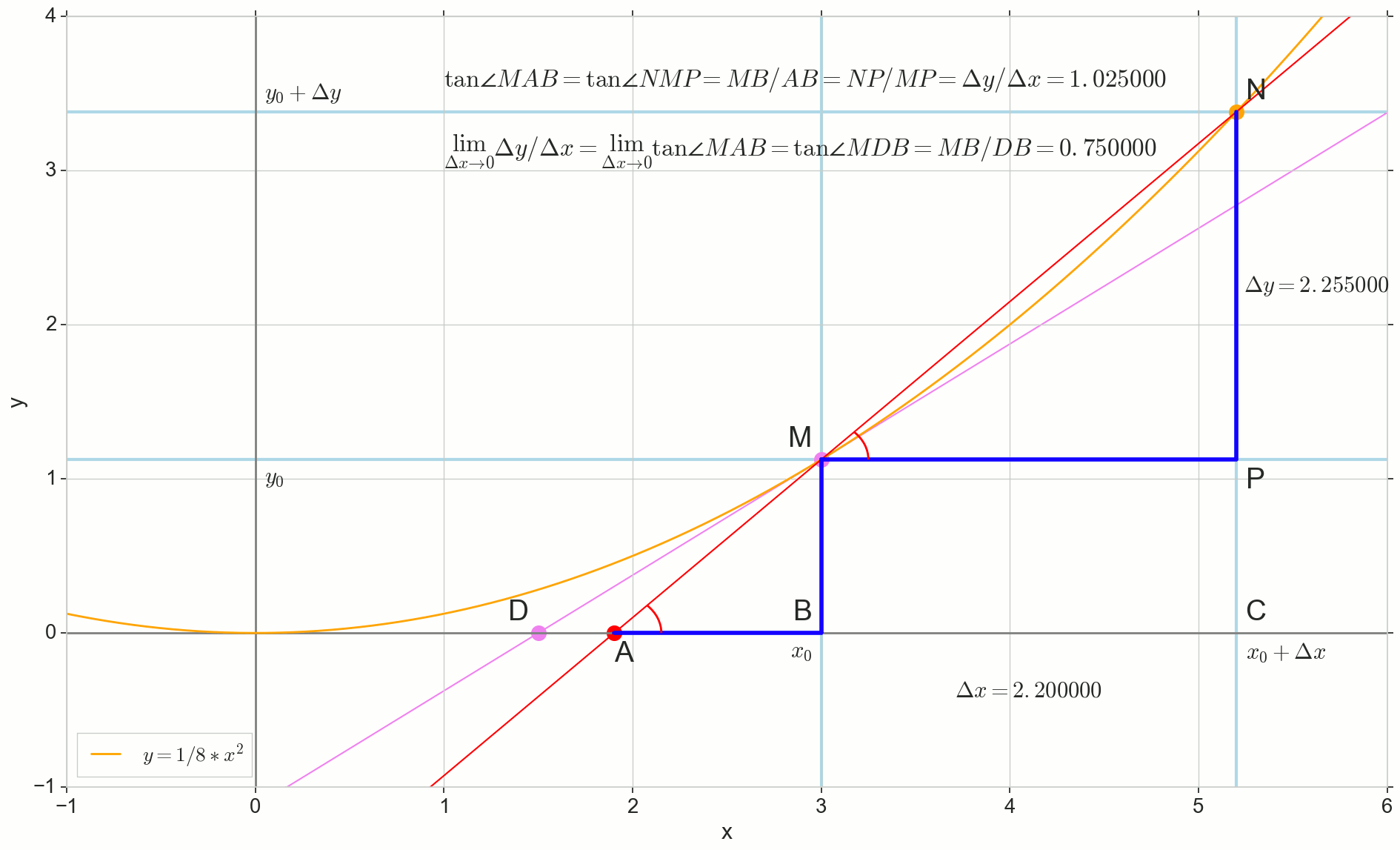
Как приращение , бесконечно приближаясь к нулю, никогда не достигнет нуля, так и точка никогда не встанет на точное место , точка не достигнет точки , треугольник не превратится в . К счастью, мы можем зафиксировать точный пункт назначения для всех этих движений, используя волшебный математический оператор «предел» .
Предел превращения треугольника — в точности треугольник , получаем:
Короче:
Вспоминая определение производной, как мы ее ввели, получаем:
И видим, что производная функции в данной точке равна тангенсу угла между касательной к исходной кривой в данной точке и горизонтальной осью координат . В этом и заключается её геометрический смысл.
Строго говоря, не совсем корректно говорить, что секущая стремится занять положение некоторой заранее известной касательной, которую мы, кстати сказать, добавили на картинку без предварительного определения. Более корректно говорить, что предельное положение секущей при приращении аргумента, стремящемся к нулю, мы будем называть касательной, т.е. мы понятие касательной выводим из определения производной (если вы посмотрите на универсальную формулу касательной, то увидите, что она задается через производную). Но сути дела это не меняет: производная численно равна тангенсу, тангенс характеризует наклон (кстати, в английском языке касательная — это tangent line, может быть интересно разобраться, кто от кого происходит — касательная от тангенса или тангенс от касательной).
В итоге отметим интересные нам свойства производной:
- Производная функции в точке равна тангенсу угла между касательной к исходной кривой в этой точке и горизонтальной осью
- По модулю — это отношение координаты точки по вертикальной оси к длине горизонтального отрезка — расстоянию между точкой на оси и точкой пересечения касательной и оси
- Чем «круче» исходная кривая, тем вертикальное расстояние больше горизонтального, тем больше абсолютное значение тангенса и производной
- Знак производной — направление спуска: слева направо — минус, справа налево — плюс
- (чтобы понять, откуда он берется, посмотрите, как в том и другом случае получается )
Вот, например, наш случай с параболой:

Оранжевая линия — исходная функция, красная линия — касательная к исходной функции в точке , синяя линия — это производная исходной функции в каждой из точек. Две зеленые линии — катеты прямоугольного треугольника с гипотенузой — касательной. Отношение вертикальной зеленой линии к горизонтальной — тангенс острого угла между касательной и горизонтальной осью , оно же — абсолютное значение производной в этой точке.

Как видим, чем ближе минимум исходной функции, тем более пологий спуск, тем меньше вертикальная зеленая линия по сравнению с горизонтальной, тем меньше абсолютное значение производной. В правой части графика (спуск справа налево, функция возрастает) производная везде больше нуля (геометрически: угол между касательной и осью острый, тангенс острого угла больше нуля).

Спуск слева направо (исходная функция убывает): все то же самое, только со знаком минус (геометрически: угол между касательной и осью тупой, тангенс тупого угла меньше нуля).
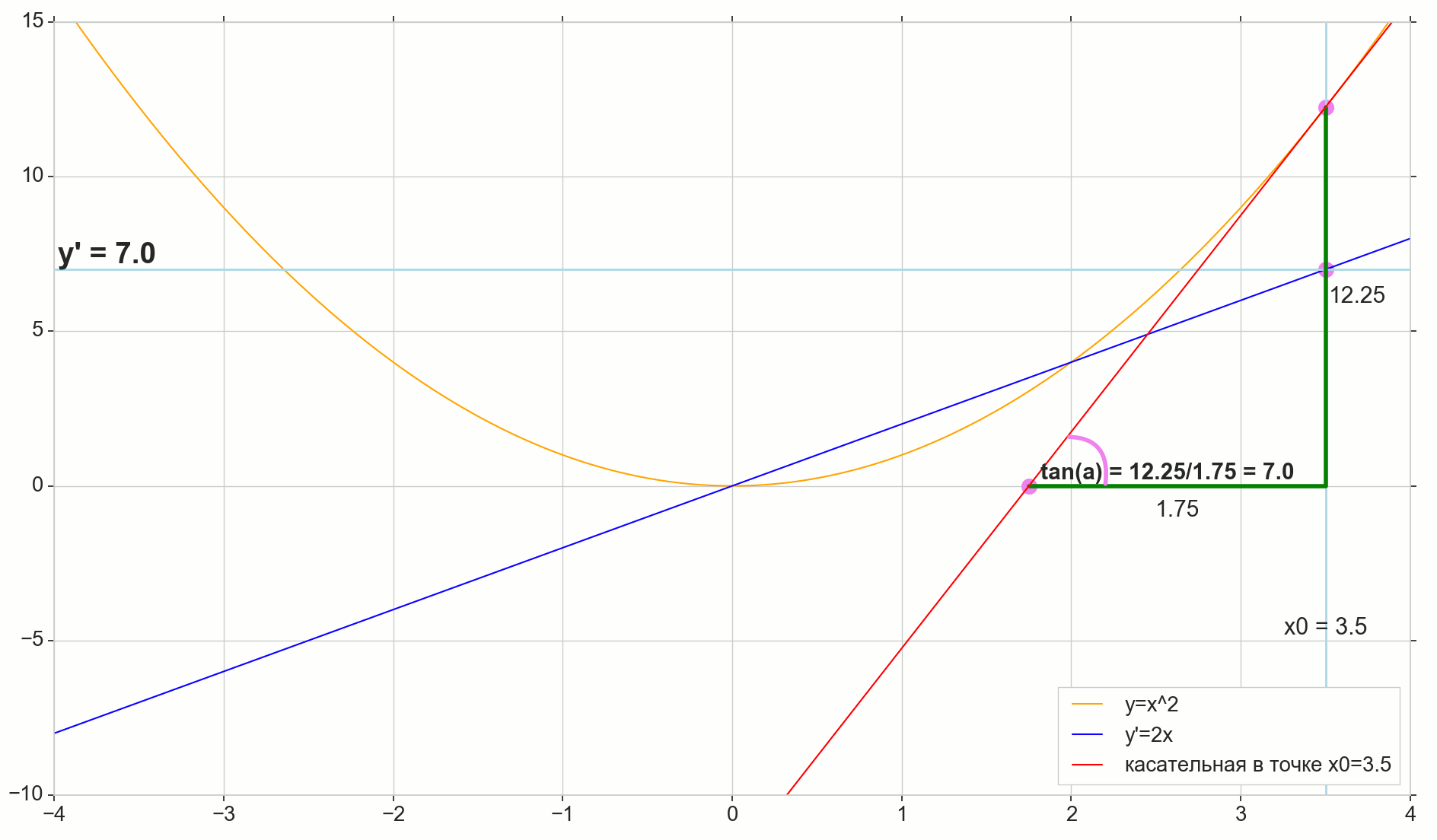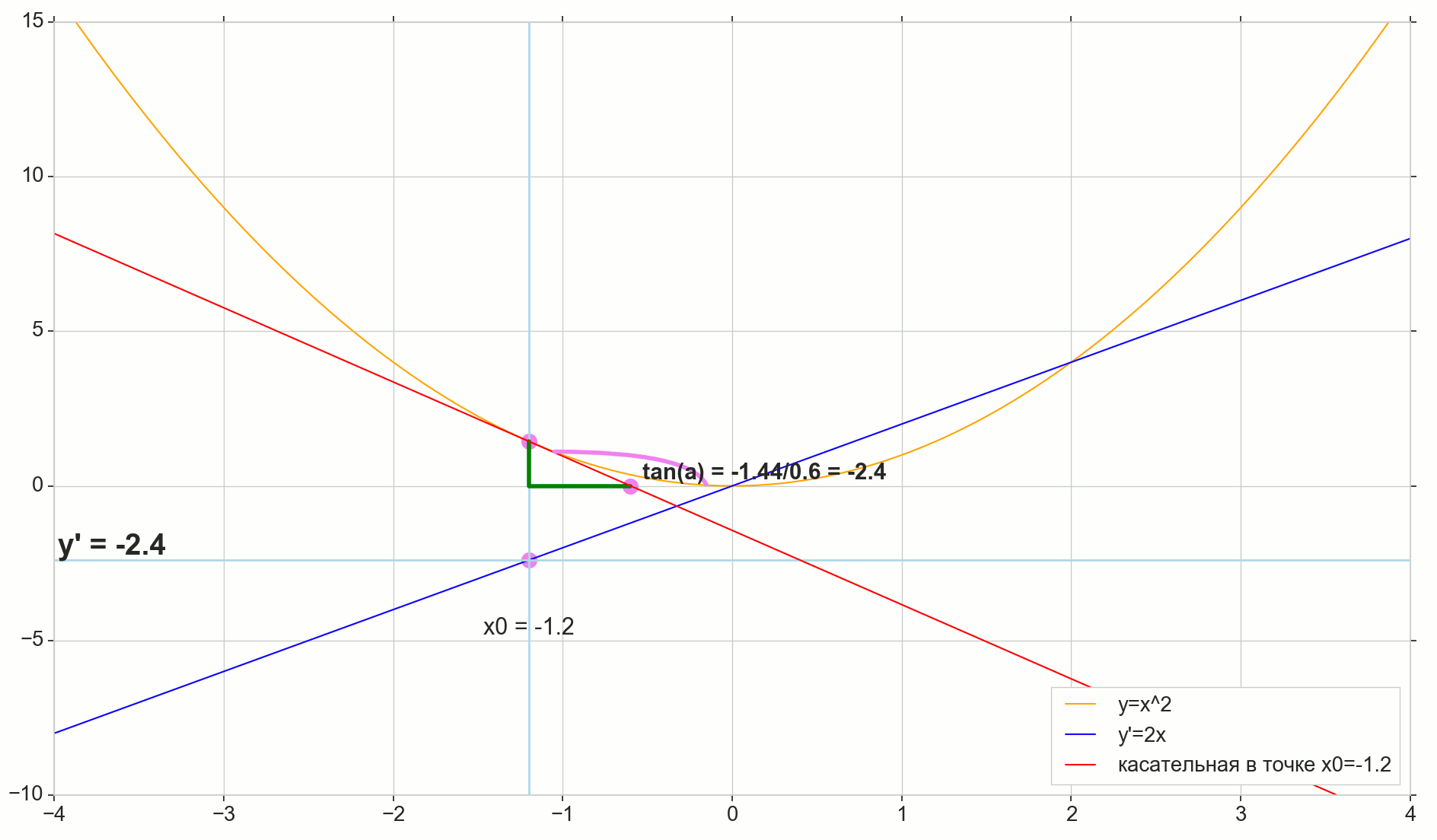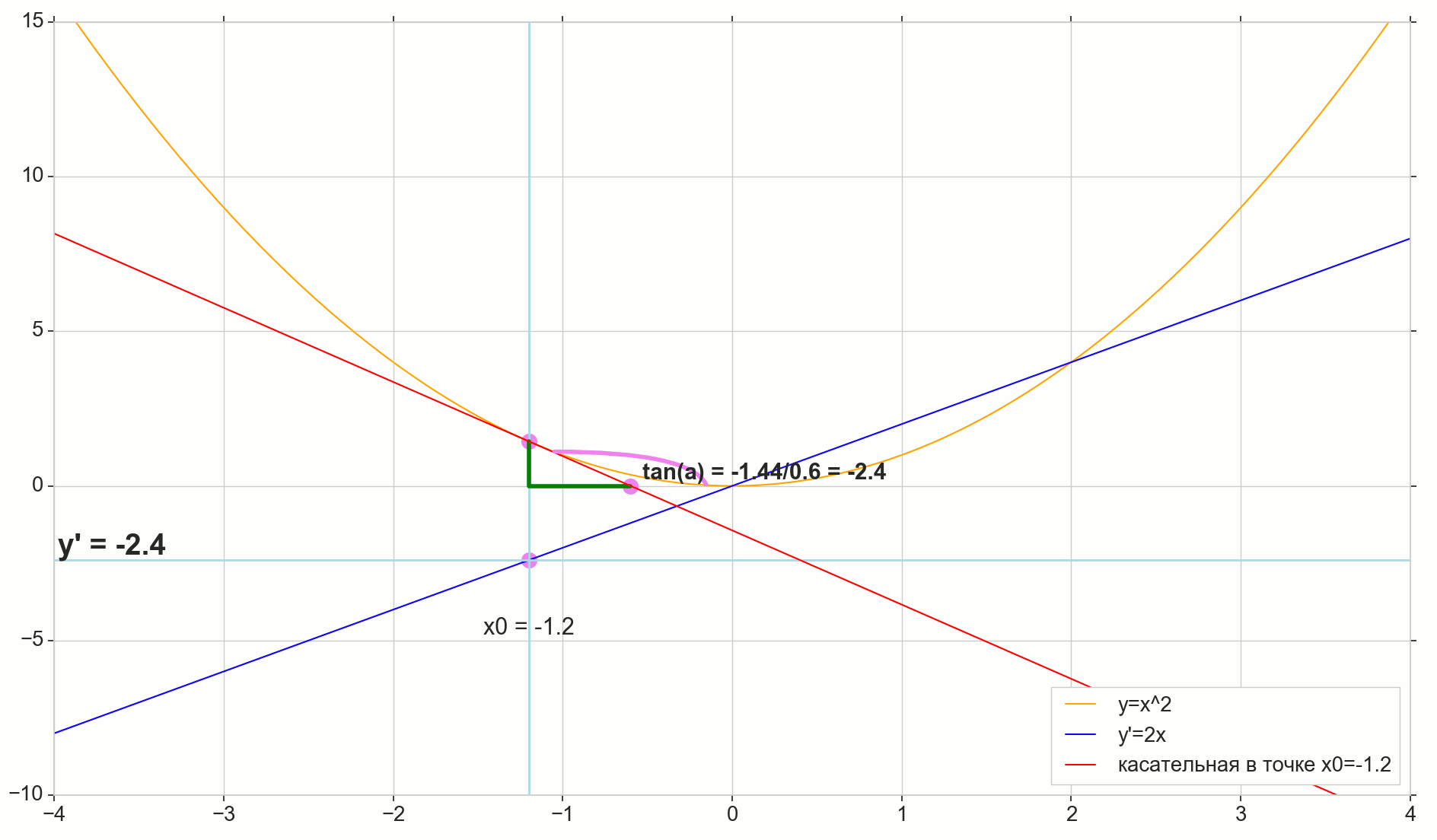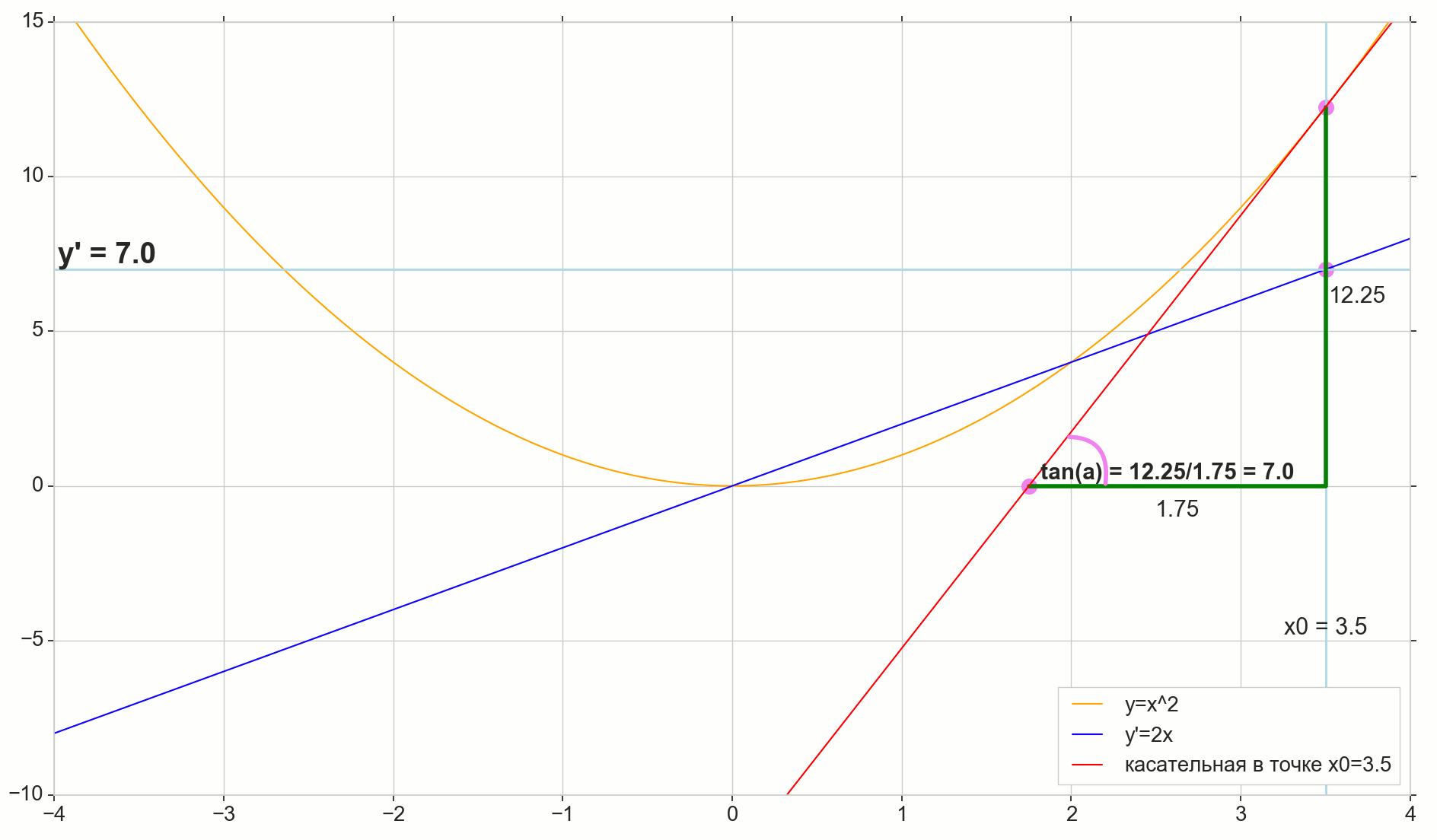
Значит, подытожим: у нас есть универсальный вычислимый индикатор (метрика), который показывает как «крутизну»/«пологость» спуска, так и его направление в каждой из точек. Этот индикатор — производная функции в каждой точке. И, раз у нас есть такой индикатор, почему бы нам не использовать его для вычисления динамического шага при спуске к минимуму данной функции? Ровно это мы сейчас и сделаем.
Частная производная по вектору
Возвращаемся к нашей функции ошибки . Мы уже видели, что, хотя она у нас является многомерной, в каждом из измерений ее можно порезать на параболы.
- Выбираем -й элемент вектора
- Считаем, что он изменяется
- Берем по нему производную
- При этом остальные элементы считаем константами
Кого испугали эти четыре строчки формул, не бойтесь: здесь производная суммы равна сумме производных, производная степенной функции, производная сложной функции, производная константы (равна нулю) и другие правила взятия производной из школьной программы. Все элементы, рядом с которыми нет множителя (обратите внимание, он может прятаться внутри общей суммы), берутся за константы. И еще, кстати, обратите внимание, наша перед SSE сократилась именно здесь.
Получили в общем виде:
И вот наш градиент — вектор из частных производных (обозначается символом [набла], перевернутым треугольником, т.е. перевернутой [дельтой]):
Определяем правило шага:
Оно же для -го измерения:
Здесь обратим внимание на:
- минус перед градиентом
- коэффициент [эта] — коэффициент обучения, некоторая константа
Те из вас, кто не пропустил часть с геометрическим смыслом производной, скорее всего уже поняли, зачем они здесь нужны. В любом случае, и то и другое подробно разберем ниже.
Наш 1-мерный случай:
Частные производные (элементы градиента):
Шаги по каждому из измерений:
Между прочим, у нас уже все готово для спуска. Давайте построим графики и спустимся по одному из измерений.
Разбор спуска по одному () из измерений
Фиксируем , спускаемся к минимуму
Сумма квадратичных ошибок для элементов обучающей выборки с правильными ответами (истинными классами) при выбранных коэффициентах и (будем дальше ссылаться на эту функцию):
def sse_(X, y, w0, w1):
return ((w0+w1*X - y)**2).sum()Посчитаем ошибки на отрезке от -1.5 до 1.5.
# наиболее удачный по наглядности вариант
w0 = 1
w1 = np.linspace(-1.5, 1.5, 200)
# должен быть способ сделать то же самое без цикла с матричной операцией через numpy.dot
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html
# но здесь так нагляднее, так что ок и так
sse = []
for i in range(len(w1)):
sse.append(sse_(X1, y, w0, w1[i]))
sse = np.array(sse)Построим график функции стоимости и заодно отметим первую точку, из которой будем спускаться (вообще говоря, она может быть любая, в том числе случайная):
plt.subplot(3,1,1)
# sse
plt.plot(w1, sse/2, color='red', label='w0=1')
# спуск - первая точка
w1_first = .9
plt.scatter(w1_first, sse_(X1, y, w0, w1_first)/2, color='blue', marker='o', s=100)
plt.xlim(-1.2, 1.2)
plt.xlabel(u'w1')
plt.ylabel(u'J(w1, w0=1)')
plt.legend(loc='lower left')
Градиент, а точнее, частная производная — элемент градиента:
grad_w1 = []
for i in range(len(w1)):
grad = ((w0 + w1[i]*X1 - y)*X1).sum()
grad_w1.append(grad)
plt.subplot(3,1,3)
plt.plot(w1, grad_w1, label=u'градиент ?J(w)/?w1')
plt.xlim(-1.2, 1.2)
plt.xlabel(u'w1')
plt.ylabel(u'?J(w)/?w1')
plt.legend(loc='upper left')
Шаги спуска (да, здесь размер шага зависит от текущего значения , т.е. шаг зависит от того, из какой точки мы шагаем):
eta = 0.001
delta_w1 = []
for i in range(len(w1)):
grad = ((w0 + w1[i]*X1 - y)*X1).sum()
delta = -eta*grad
delta_w1.append(delta)
plt.subplot(3,1,2)
plt.plot(w1, delta_w1,
color='orange', label=u'?w1, ?=%s'%eta)
plt.xlim(-1.2, 1.2)
plt.xlabel(u'w1')
plt.ylabel(u'?w1=-?*?J(w)/?w1')
plt.legend(loc='upper right')
Все вместе
plt.show()
Здесь видим
- Наверху: график выпуклой функции, имеется глобальный минимум
- Внизу: частная производная — показывает степень «крутизны» функции наверху (чем больше производная, тем «круче» функция), знак определяет направление
- Посередине: шаг для спуска — частная производная со знаком минус (чтобы спускаться в сторону минимума), помноженная на коэффициент [эта] (он же коэффициент обучения), определяющий размер шага
Обратите внимание на масштаб по вертикальным осям на двух нижних графиках: экранные размеры у них одинаковые, но абсолютные значения отличаются в 1000 раз.
Ну давайте уже, наконец, спускаться
Исходные веса — обычно это какие-то случайные не очень большие значения или какие-то константы. Мы договорились взять , а исходную точку спуска . Здесь же выберем коэффициент обучения и количество итераций (количество шагов, количество эпох обучения) пусть будет 12:
# норм спуск за 12-14 эпох
eta = 0.001
epochs = 12Посчитаем значения шагов и значения ошибок на каждом новом шаге:
# спуск по точкам по градиенту
w1_epochs = [w1_first]
delta_w1_epochs = []
w1_next = w1_first
for i in range(epochs):
grad = ((w0 + w1_next*X1 - y)*X1).sum()
delta = -eta*grad
w1_next = w1_next + delta
delta_w1_epochs.append(delta)
w1_epochs.append(w1_next)
# последняя дельта - 0
delta_w1_epochs.append(0)
w1_epochs = np.array(w1_epochs)
delta_w1_epochs = np.array(delta_w1_epochs)
# квадратичные ошибки по эпохам
sse_epochs = []
for i in range(len(w1_epochs)):
sse_epochs.append(sse_(X1, y, w0, w1_epochs[i]))
sse_epochs = np.array(sse_epochs)Обозначим точки спуска с длинами шагов по на графике :
# размер точек на графике - уменьшается от первой эпохи к последней
size_epochs = [10 + (250-100)*epoch/epochs for epoch in reversed(range(epochs+1))]
plt.scatter(w1_epochs, sse_epochs/2, color='blue', marker='o', s=size_epochs,
label=u'спуск по градиенту, ?=%s'%eta)
# длины шагов по w1
plt.plot([w1_epochs, w1_epochs+delta_w1_epochs], [sse_epochs/2, sse_epochs/2],
color='orange')#, label='?w1')
И те же точки спуска с длинами шагов на графике
plt.scatter(w1_epochs, delta_w1_epochs, color='blue',
marker='o', s=size_epochs,
label=u'спуск по градиенту, ?=%s'%eta)
plt.plot([w1_epochs, w1_epochs],
[delta_w1_epochs, np.zeros(len(delta_w1_epochs))],
color='orange')
Да, это он, спуск по градиенту (по одному из его измерений), градиентный спуск. В этом месте можно тоже испытать просветление, не такое сильное, как первое, конечно.
Процедура спуска: для текущей точки на верхнем графике смотрим длину и направление шага на среднем графике, на верхнем графике откладываем шаг из текущей точки, движемся по линии шага на верхнем графике, «падаем» с нее на график, место падения — новая отправная точка, повторяем процедуру.
- На всех графиках горизонтальная ось — параметр на одном и том же отрезке, вертикальные оси — разные
- Движемся справа налево, от самой большой точки к самой маленькой
- Размер шага и направление — оранжевые отрезки на графике: на верхнем графике горизонтальные, на среднем — вертикальные
- Длина вертикального отрезка на среднем графике равна длине соответствующего горизонтального отрезка на верхнем графике, но на экране они могут не совпадать — обратите внимание на масштабы по осям
- На среднем графике отрезки с шагами, расположенные ниже нуля (правая половина), дают отрицательный шаг справа налево, выше нуля (левая половина) — положительный шаг слева направо, пересечение с нулем — строгий минимум функции ошибки
- (говоря проще и строже, здесь шаг — это просто значение вертикальной координаты на среднем графике).
- Знак перед шагом на среднем графике полностью соответствует направлению спуска на верхнем графике: в правой половине графика мы спускаемся справа налево — шаг отрицательный, в левой половине графика мы спускаемся слева направо — шаг положительный
- Откуда мы его берем? Из нижнего графика производной — она попадает на средний график со знаком минус. Вспоминаем про геометрический смысл производной.
- Посмотрим еще ближе на нижний график производной и средний график с шагом. По горизонтальной оси у них одни и те же значения , а по вертикали масштаб существенно отличается. Из геометрического смысла производной мы помним, что значение производной в данной точке можно использовать как метрику «крутости»/«пологости» исходной кривой. Чем круче кривая, тем мы дальше от минимума, тем дальше в этом месте можем шагать. Чем кривая более пологая, тем мы ближе к минимуму, тем короче нужно делать шаги, «сбавить обороты». Но посмотрите на диапазон значений на вертикальной оси нижнего графика с производной, а потом на диапазон на горизонтальной оси на верхнем графике с функцией: для исходной точки значение производной получается примерно 200, при том, что расстояние до минимума, судя по графику, в районе 1. Это значит, что значение производной как есть мы в качестве шага брать не можем, но мы можем легко отмасштабировать его так, чтобы оно попадало в нужный нам диапазон. Для этого используем специальный коэффициент — тот самый коэффициент обучения . В нашем случае нужно подобрать его значение так, чтобы значение производной 200 стало меньше 1. Берем , получаем для точки длину шага 200*0.001=0.2 (с учетом домножения на -1, точный шаг получается -0.2) — в самый раз.
- Значение ошибки в первой точке , в последней точке через 12 эпох (шагов, итераций)
- Это не реальный минимум, но мы можем приблизиться к реальному минимуму сколь угодно близко, увеличивая количество эпох
В общем, именно в этом и заключается метод градиентного спуска. С таким уточнением, что здесь мы спустились только по одной координате и попали в локальный минимум на одном срезе. Чтобы попасть в глобальный минимум многомерной функции, мы будем на каждой итерации делать по одному шагу по каждой из координат (или один шаг, но многомерный). Коэффициент обучения нужно подобрать таким образом, чтобы он обеспечил подходящий масштаб сразу для всех срезов.
Замечание: возможно, можно представить модификацию алгоритма с разными коэффициентами обучения для каждого из измерений, не скажу сейчас, есть ли в этом реальный практический смысл.
В принципе, на этом можно было бы и закончить, но давайте разберем и разжуем все совсем до жидкой кашицы, раз уж все равно до сюда добрались.
Подбираем темп обучения
Подытожим
- [эта] — коэффициент (темп) обучения
- Влияет на длину шага на каждой эпохе
- Чем меньше шаг, тем выше точность
- Но тем больше эпох требуется для спуска в минимум
- Алгоритм подбора коэффициента «наощупь»: начать с достаточно маленького значения так, чтобы алгоритм сходился, и начать увеличивать до тех пор, пока алгоритм не начнет расходиться
- Это удобнее делать, если построить график сходимости по эпохам
- Или строго осмысленно: посмотреть на диапазон значений для каждого из измерений и на значение градиента, подобрать так, чтобы отмасштабированный градиент попал в масштаб окрестности вблизи минимума
Возьмем значение
# алгоритм не сходится
eta = 0.01
epochs = 6
Здесь еще раз обратите внимание на диапазон значений по вертикальной оси на среднем графике и диапазон на горизонтальной оси наверху. Вертикальные отрезки на среднем графике по длине равны соответствующим горизонтальным отрезкам шагов на верхнем графике, хотя при экранном масштабе это не бросается в глаза. Здесь начинаем движение из точки 3-й справа, дальше перепрыгиваем через минимум в 3-ю слева, потом опять через минимум направо, налево и т.п. Каждый раз забираемся все выше по параболе, т.е. с каждым шагом ошибка возрастает. Это значит, что алгоритм расходится, нужно выбрать [эту] поменьше.
Для выбора коэффициента удобно построить график сходимости при разных по эпохам
# спускаемся по градиенту к минимуму J(w0, w1) одновременно по w0 и w1
# норм спуск за 12-14 эпох
eta = 0.001
epochs = 12
# спуск - первая точка
# берем начальные w0 и w1 - можно случайные, но возьмем так,
# чтобы спуститься за 10-15 эпох
# NB: (ответ будет зависеть от знака, а, точнее, от того,
# с какой стороны минимума начнется спуск)
w0_first = -.9
w1_first = -.9
# спуск по точкам по градиенту
w0_epochs = [w0_first]
w1_epochs = [w1_first]
delta_w0_epochs = []
delta_w1_epochs = []
w0_next = w0_first
w1_next = w1_first
for i in range(epochs):
grad_w0 = (w0_next + w1_next*X1 - y).sum()
delta_w0 = -eta*grad_w0
grad_w1 = ((w0_next + w1_next*X1 - y)*X1).sum()
delta_w1 = -eta*grad_w1
w0_next = w0_next + delta_w0
w1_next = w1_next + delta_w1
delta_w0_epochs.append(delta_w0)
delta_w1_epochs.append(delta_w1)
w0_epochs.append(w0_next)
w1_epochs.append(w1_next)
# квадратичные ошибки по эпохам
sse_epochs = []
for i in range(len(w1_epochs)):
sse = sse_(X1, y, w0_epochs[i], w1_epochs[i])
sse_epochs.append(sse)
print('epoch=%d, w0=%f, w1=%f, SSE/2=%f' % (i, w0_epochs[i], w1_epochs[i], sse/2))
sse_epochs = np.array(sse_epochs)
# график - ошибка от эпохи при выбранном ? (-эта-)
plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, ?=%s'%eta)
plt.xlabel(u'epoch (?=%s)'%eta)
plt.ylabel(u'J(w)')
plt.legend(loc='upper right')
plt.show()
Так сходимся: ошибка падает на каждой эпохе, причем в первые эпохи довольно быстро, дальше падение замедляется. Кстати, здесь уже спускаемся по всем координатам сразу — это реальный многомерный алгоритм, градиентный спуск, уже совсем без оговорок.
Эпох можно взять чуть побольше с запасом:
# пятьдесят попыток
eta = 0.001
epochs = 50
А вот так расходимся:
# алгоритм не сходится
eta = 0.01
epochs = 8
Ошибка растет.
Подбираем количество эпох
Алгоритм должен успеть спуститься вниз при заданном темпе обучения . Идеальный минимум получить не можем, но можем приблизиться к нему настолько близко, насколько захотим.

Здесь темп ок, эпох маловато.
На практике количество эпох удобнее выбрать одним из двух способов:
- Строго: сравнить ошибку на текущем шаге с ошибкой на предыдущем шаге, остановиться тогда, когда разница будет меньше некоторого заранее заданного значения (уровень точности). Чтобы избежать бесконечного цикла, останавливаться также, если нужная точность не достигнута после максимального количества итераций, или в том случае, если ошибка растет.
- На глаз: по графику сходимости.
Кстати, ответ (конкретное значение ошибки) будет зависеть от исходных значений весов , в том числе от того, с какой стороны минимума начнется спуск. Если, например, первоначальные веса задаются случайно, мы будем каждый раз получать разные значения ошибки через одно и то же количество эпох. Нас интересует не точное значение ошибки, а то, насколько близко к минимуму оно приблизилось.
Воронка потерь, одеяло потерь
Вернемся к графику функции потерь, понаблюдаем спуск воочию.
Начальная позиция, начинаем спуск:

Первый шаг — движемся в сторону воронки:
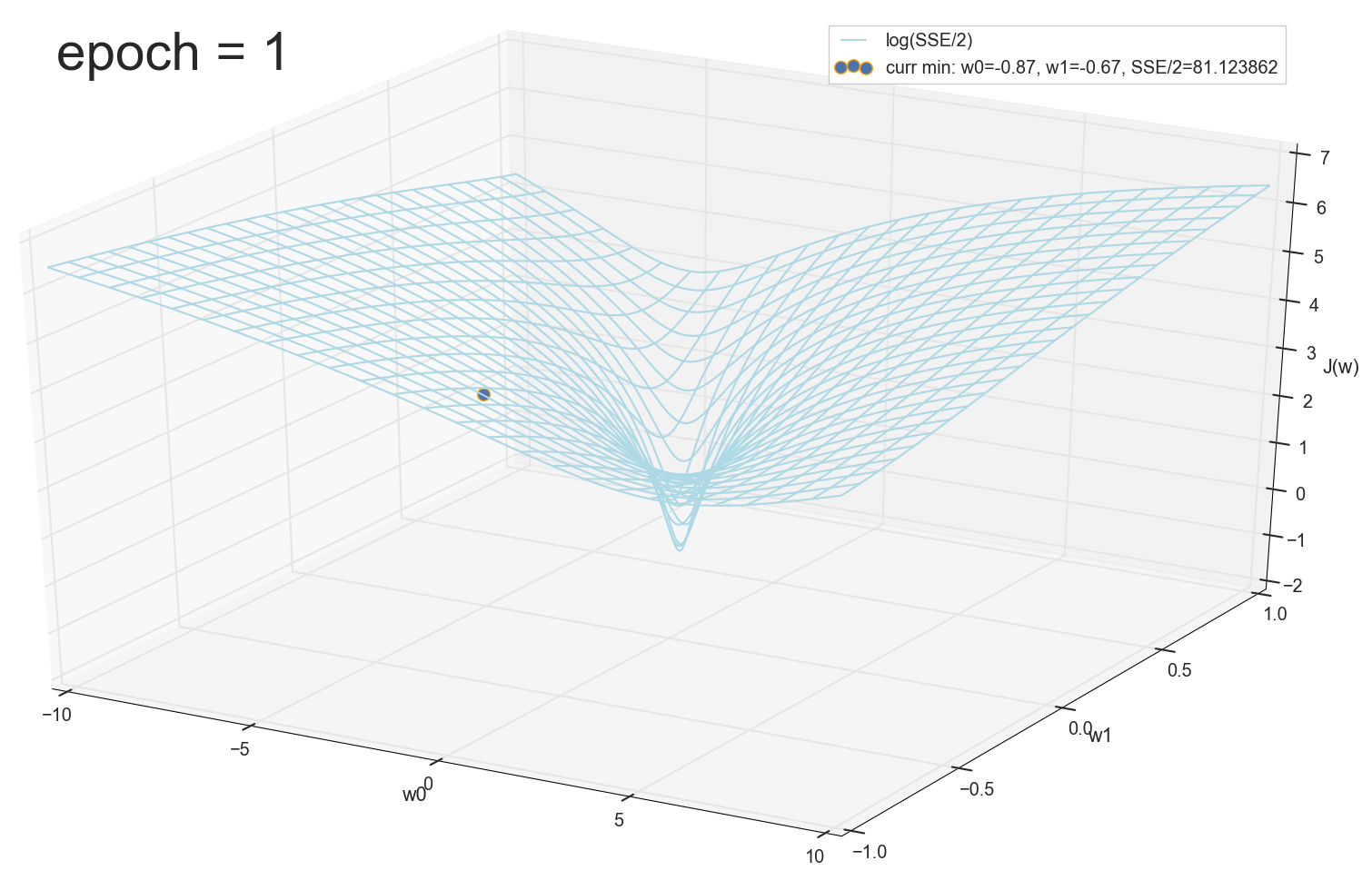
Через 12 эпох — глубоко внутри воронки, но не на самом дне:

Через 50 эпох:

Через 1767 эпох — получаем первый раз ошибку меньше, чем поиск по сетке:

Это фактически и было дно, через 62000 эпох результат лучше не сильно:

По шагам:
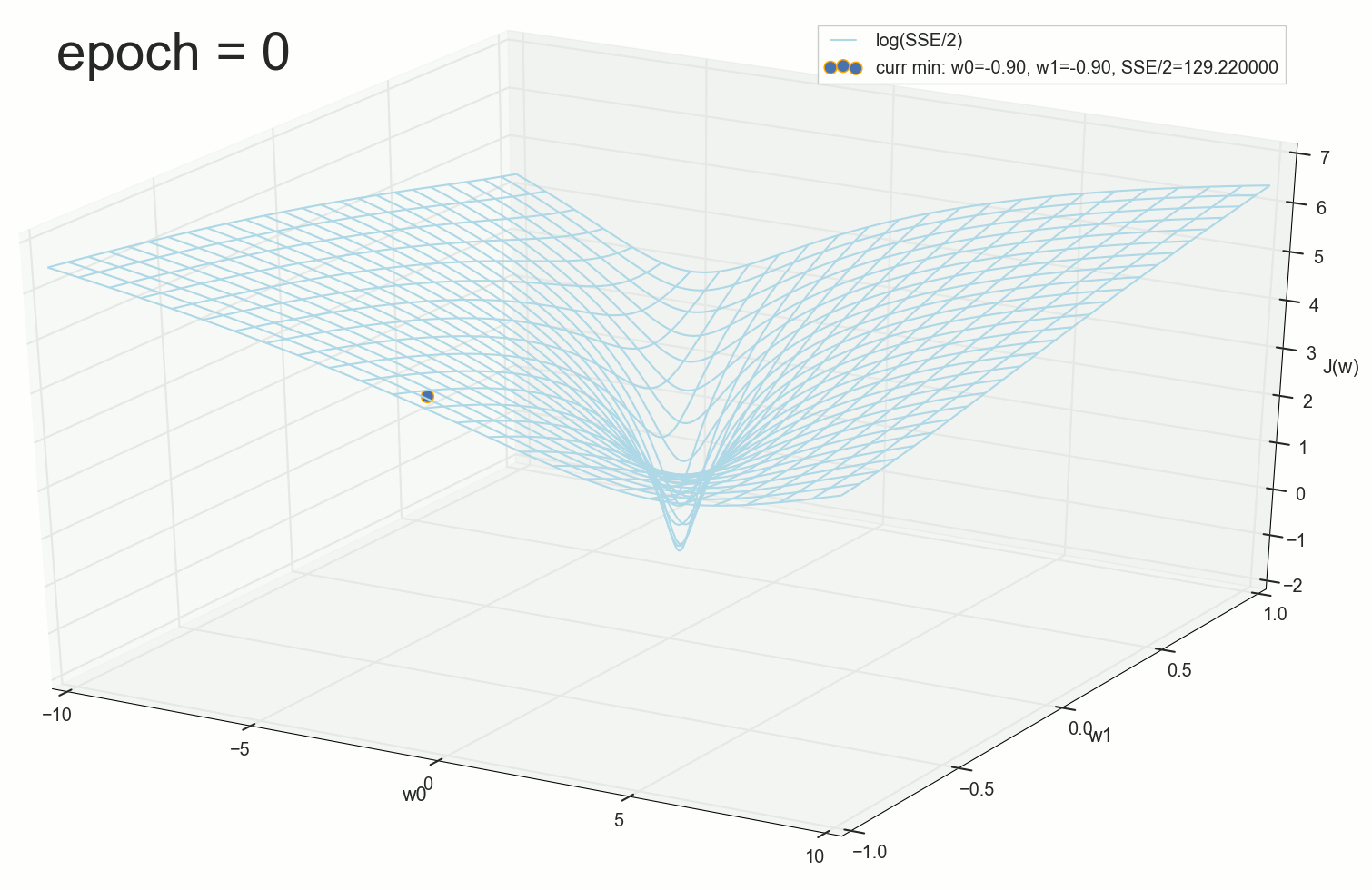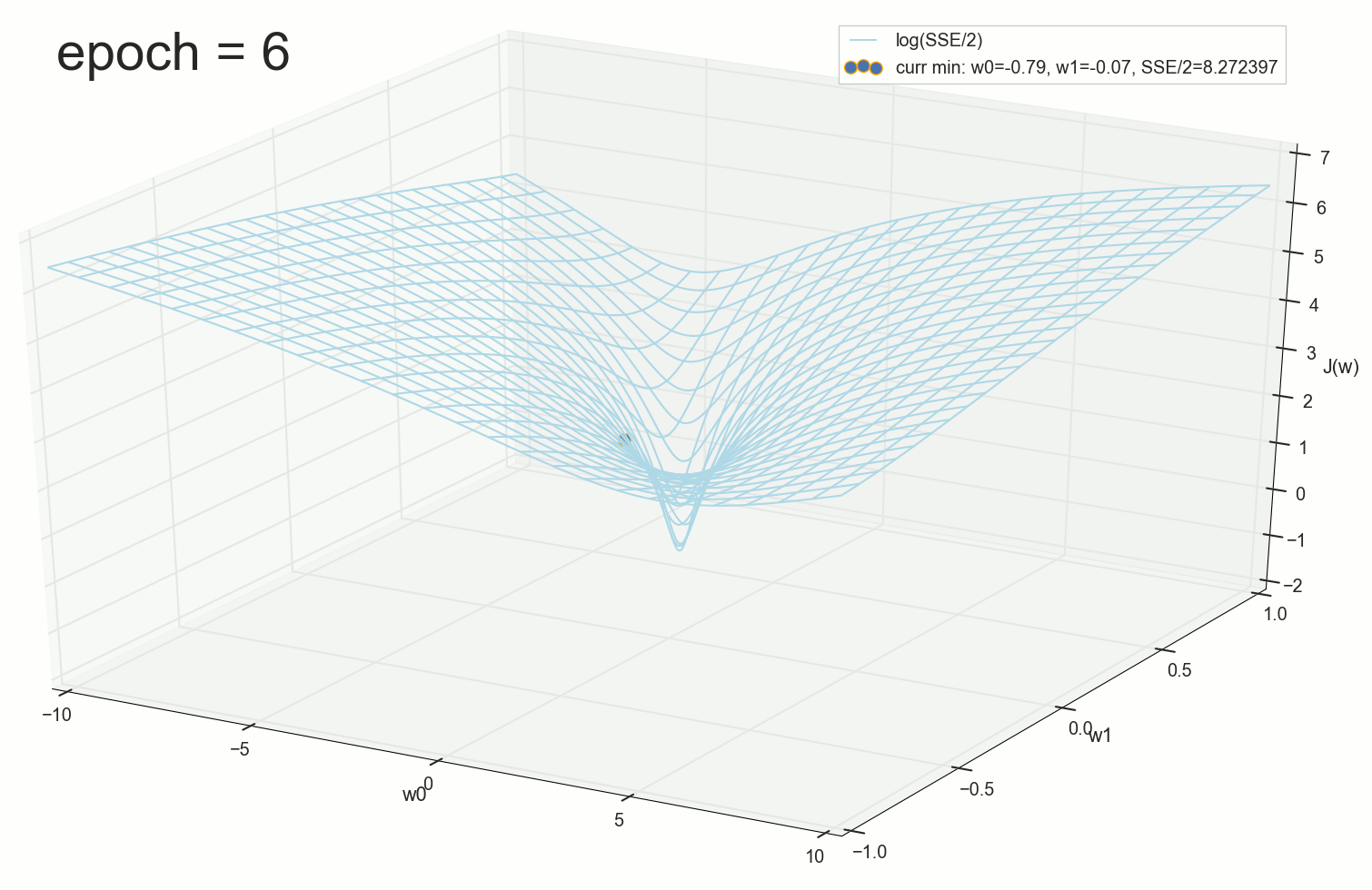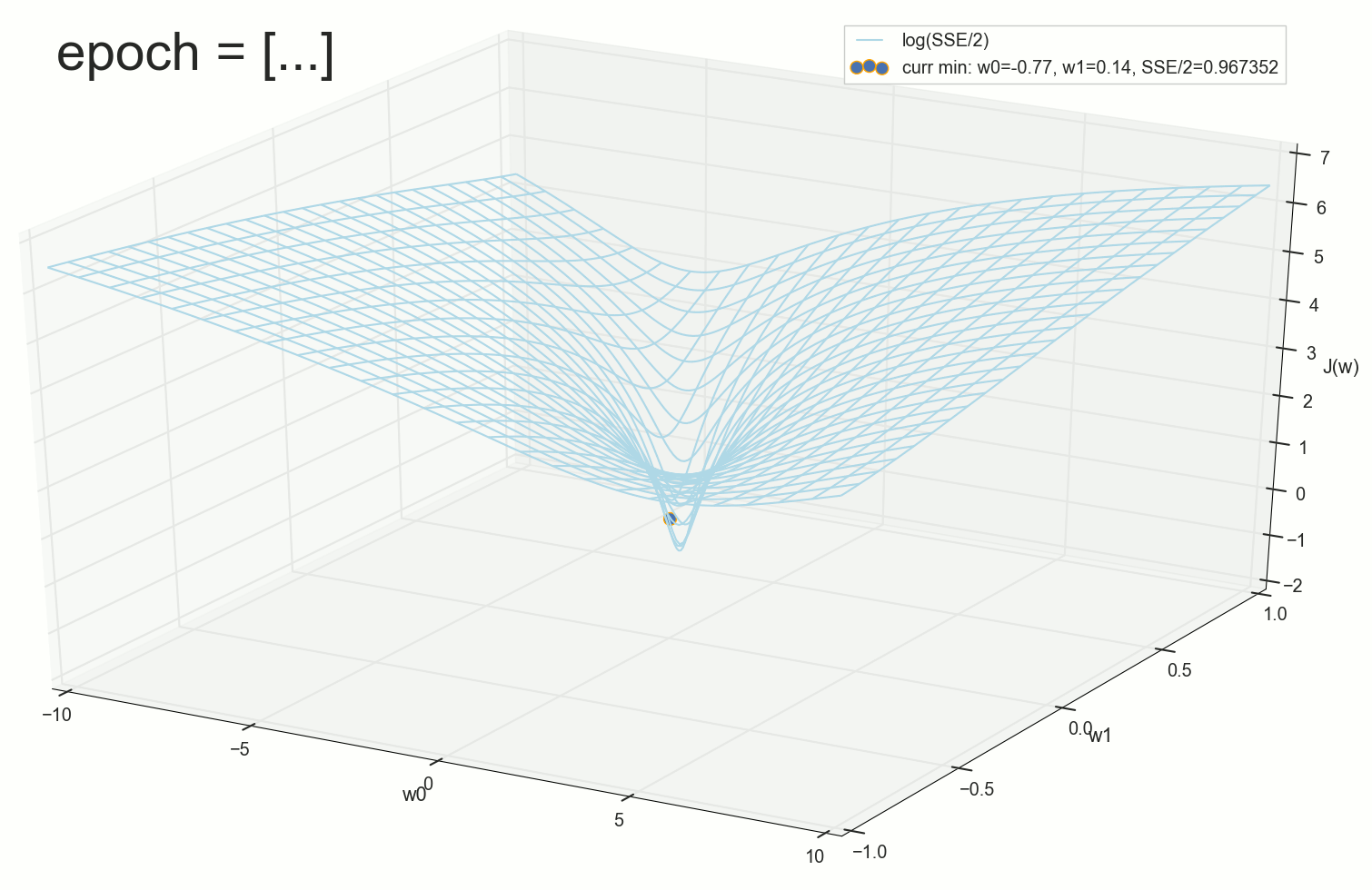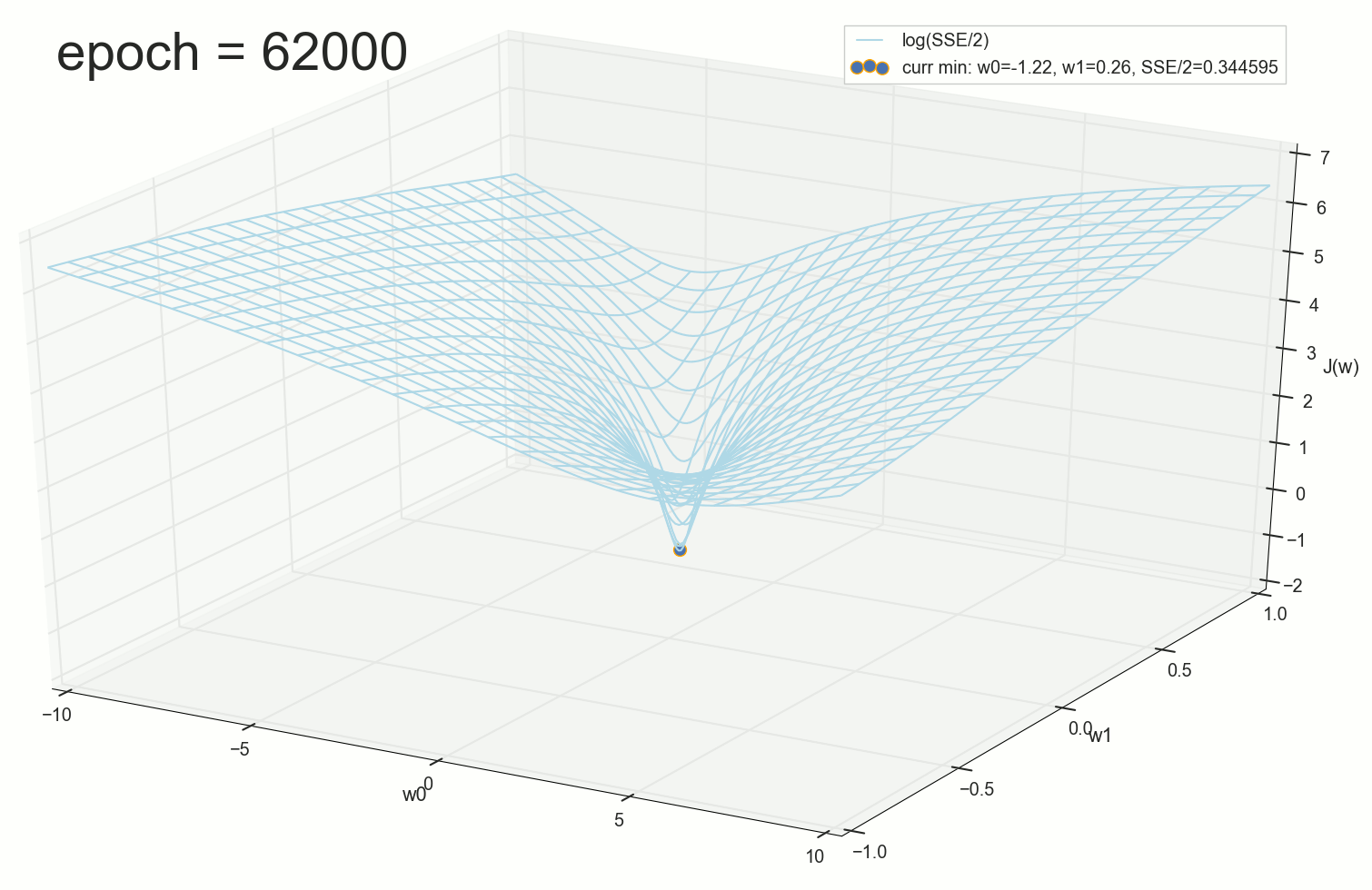
Шарик неотвратимо скатывается на дно воронки. Кажется, что в этом нет ничего удивительного: вот мы видим шарик, вот видим воронку, совершенно логично шарику катиться по стенкам вниз. Однако, здесь стоит вспомнить, что шарик здесь скатывается по стенке не потому, что нам так захотелось его нарисовать, а потому, что такие шаги подбирает для него наш алгоритм, основанный на математике градиентного спуска. Нам теперь понятно, почему так происходит, но в этом все-таки заключается небольшое математическое волшебство.
И еще, возможно, кто-то сейчас заметил, что на этом графике в процессе скатывания есть что-то не то: на верхней пологой части склона шарик катится очень быстро и достигает воронку за несколько шагов, после чего внутри самой воронки с почти отвесными стенками замедляется на несколько порядков и дно достигает вообще через полторы тысячи шагов, хотя, по идее, на пологой части движение должно быть медленнее, а на крутых склонах — максимально быстрое. Понятно, что у нас здесь никакая не гравитация, но, если мы вспомним геометрический смысл производной и принцип, по которому мы подбирали шаг, то все равно, на крутых склонах шаг должен быть большим, на пологих спусках — все меньше и меньше. В чем же дело?
А просто вспомним, что на этом графике вертикальная шкала у нас логарифмическая. На самом деле поверхность спуска выглядит так:
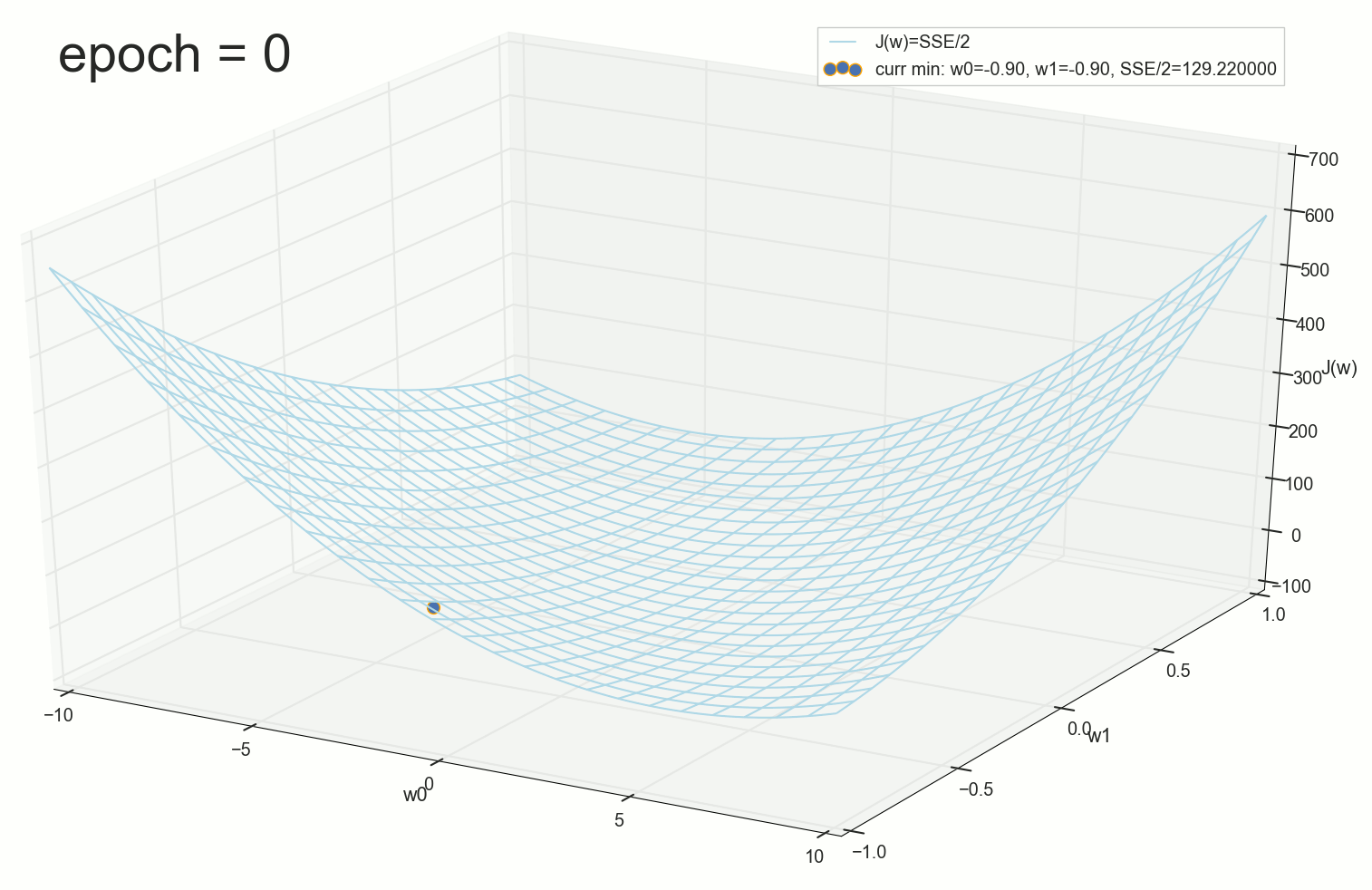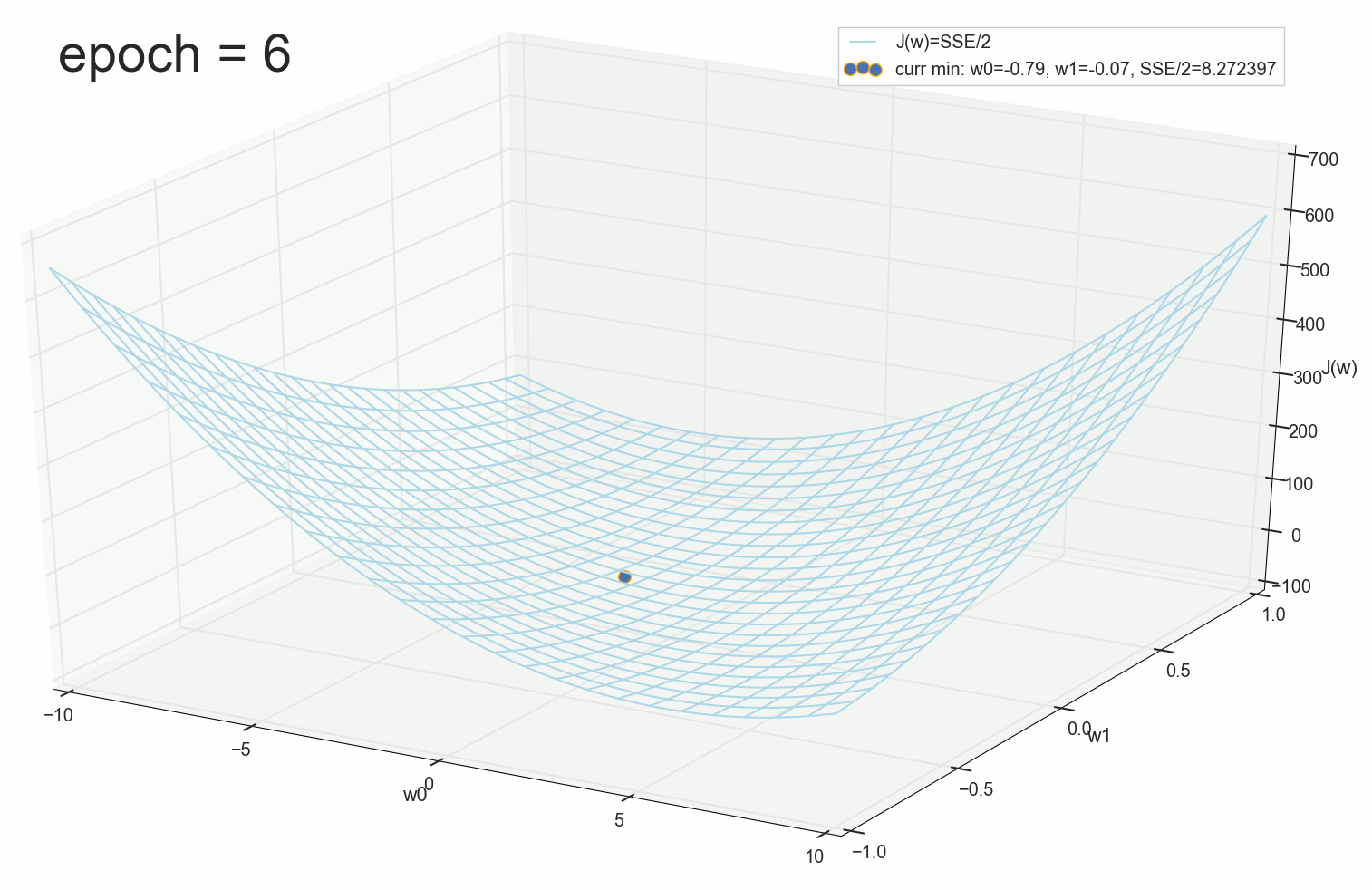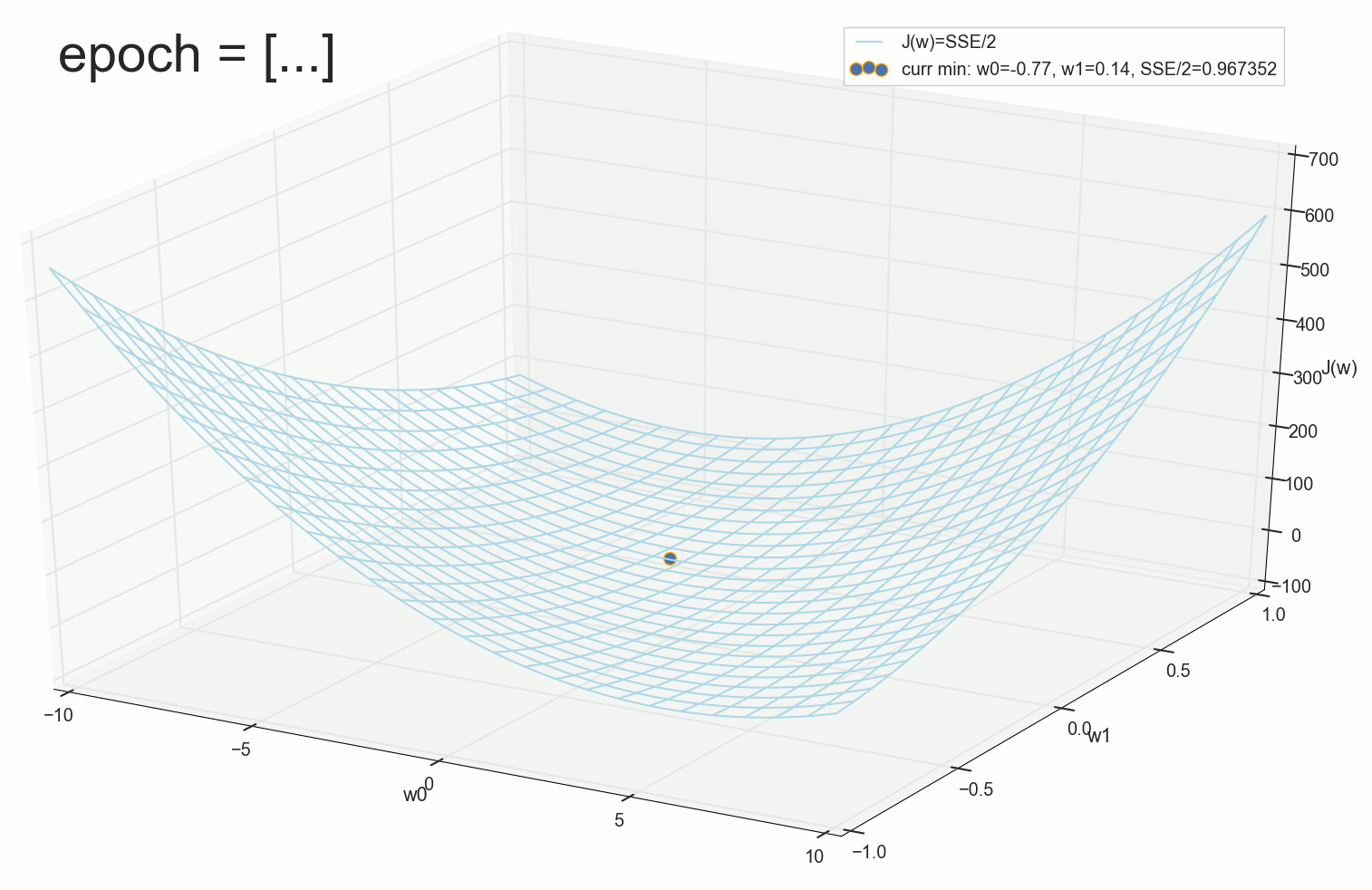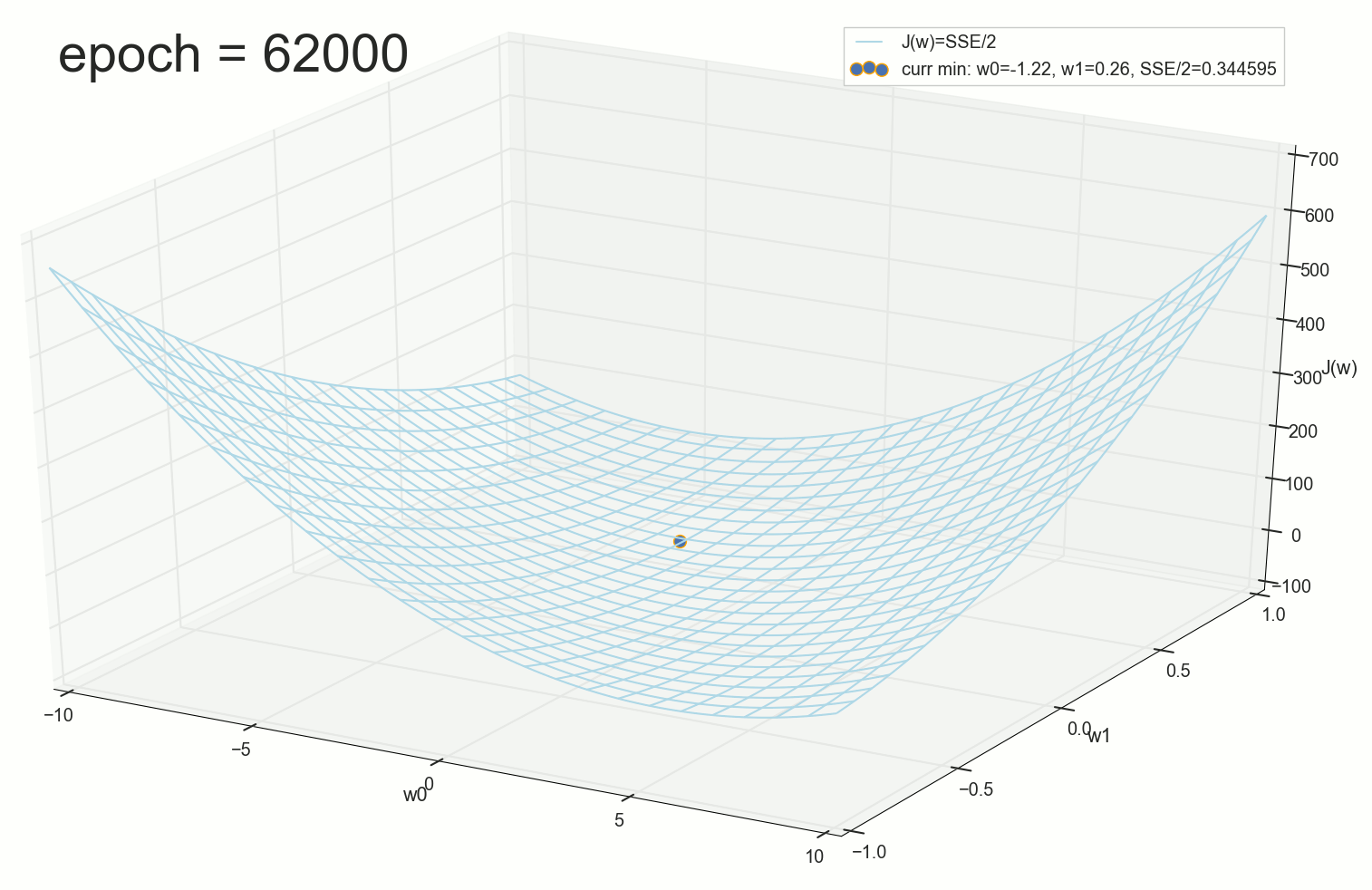
Короче, поверхность спуска у нас не воронка, а гамак (или подвешенное за концы провисшее одеяло). Для интуитивного понимания геометрического смысла спуска по производной лучше смотреть на этот график: чем круче наклон функции, тем быстрее спуск. Хотя воронка, конечно, живописнее.
Активация на резиночках
Посмотрим еще на функцию активации. С нее начинали, к ней вернулись.
Начальная позиция. То, что линии ошибок неплохо укоротить, видно невооруженным глазом. Для всех синих точек активация предсказывает неправильный класс, для красных — правильный.

Первый шаг — ошибки потихоньку начинают ужиматься:

К 11-му шагу активация заметно уехала наверх и сменила направление наклона: двум синим точкам теперь назначает правильный класс, но для одной синей точки класс все еще неправильный; правильный класс для красных точек сохранился:

12-й шаг: классы для всех точек назначены правильно, но есть ощущение, что можно лучше:

50-я попытка: лучше, чем 12-я

Шаг 1766: вот линия активации лежит уже довольно красиво. Функция ошибки на этой эпохе — это все еще больше, чем ошибка, найденная вручную по сетке (там была : разницу видно только в 6-м знаке, причем, если до него не округлять)

Шаг 1767: ошибка — это лучше, чем ручной результат (разница в 6-м знаке, можно с округлением). Искомые коэффициенты , ( заметно отличается от посеточных вариантов в пределах 2-х знаков: , )

Шаг 62000: ошибка — получше, но совсем не радикально (в 2-х знаках после запятой разницы не видно). По внешнему виду графики почти не отличить:

в динамике:
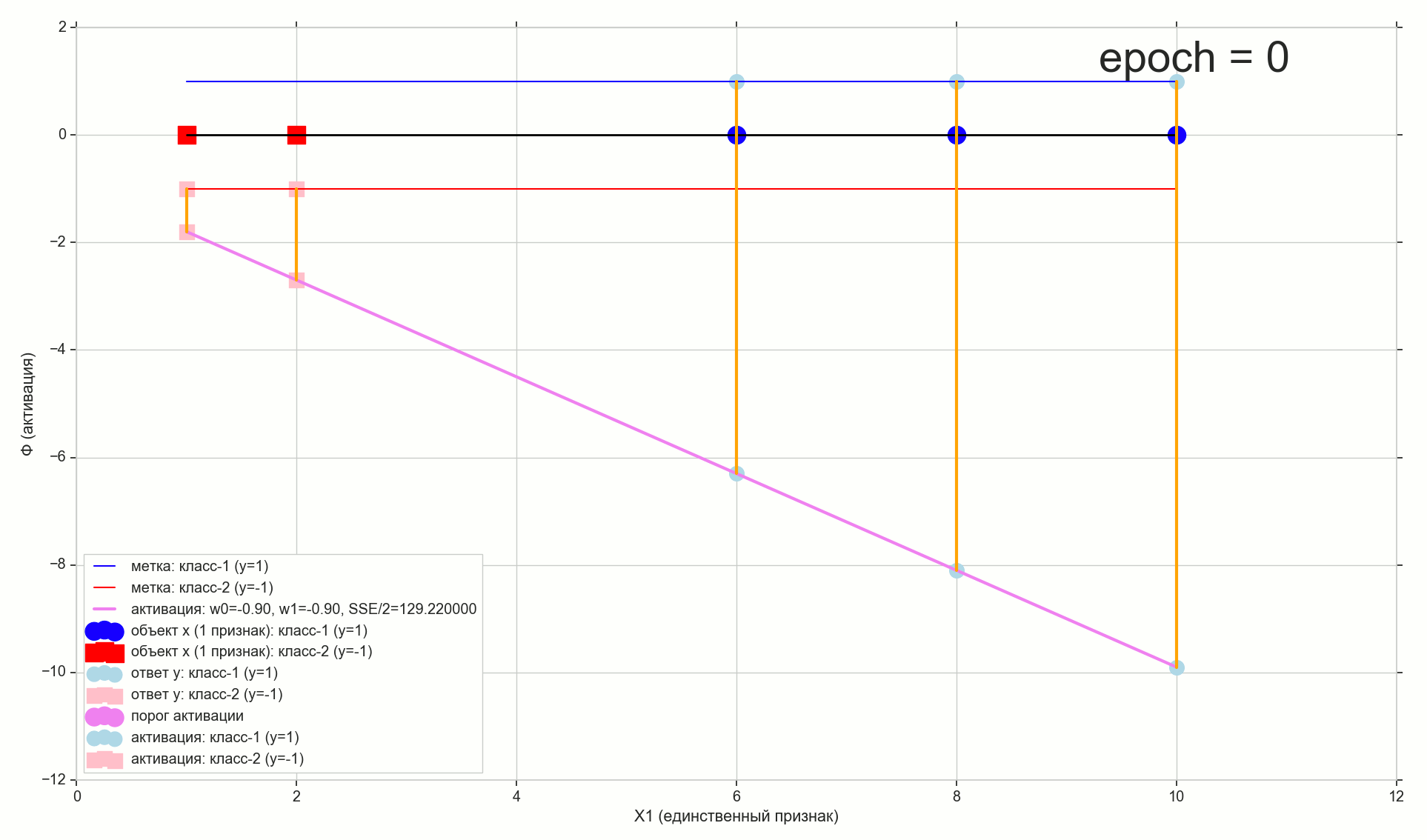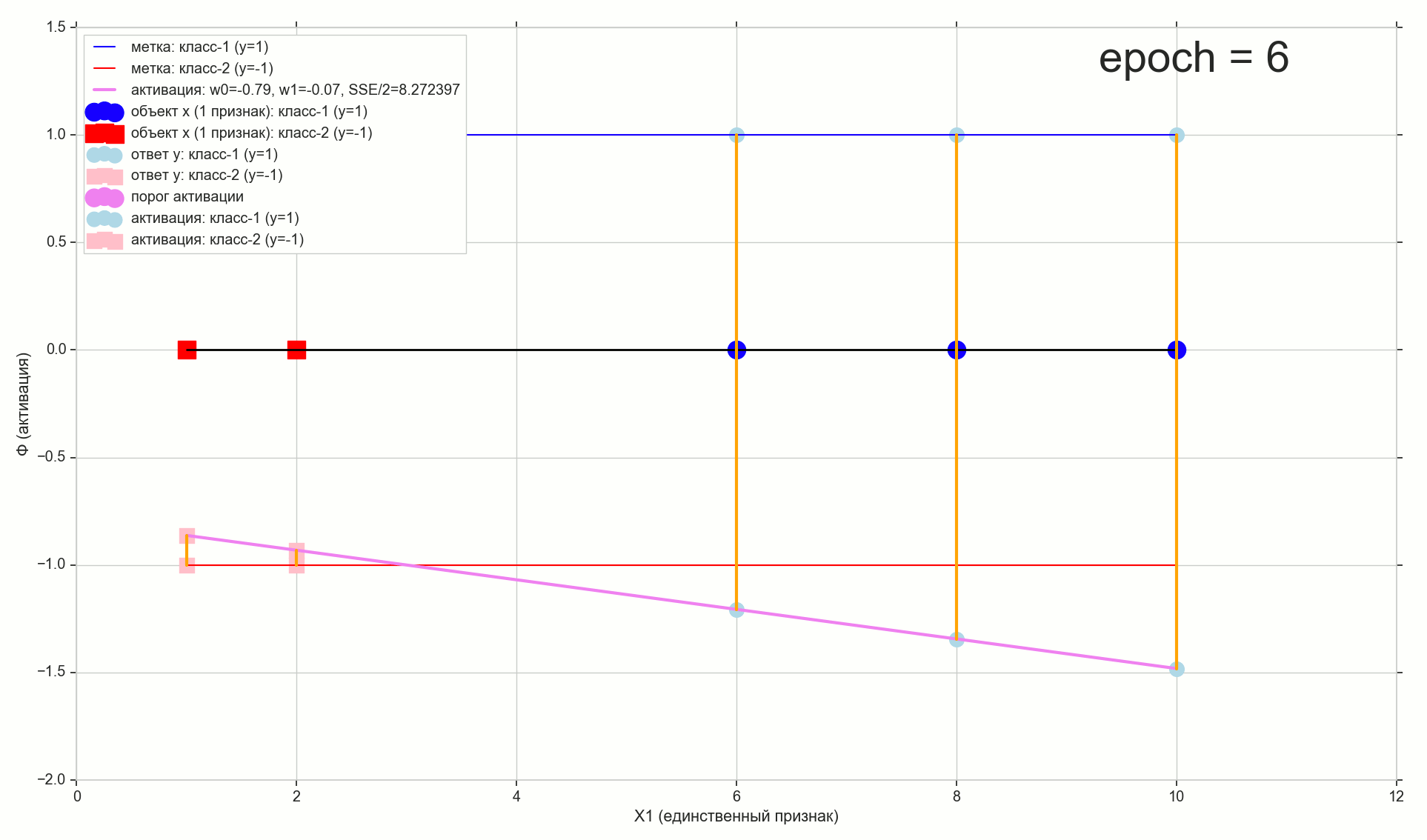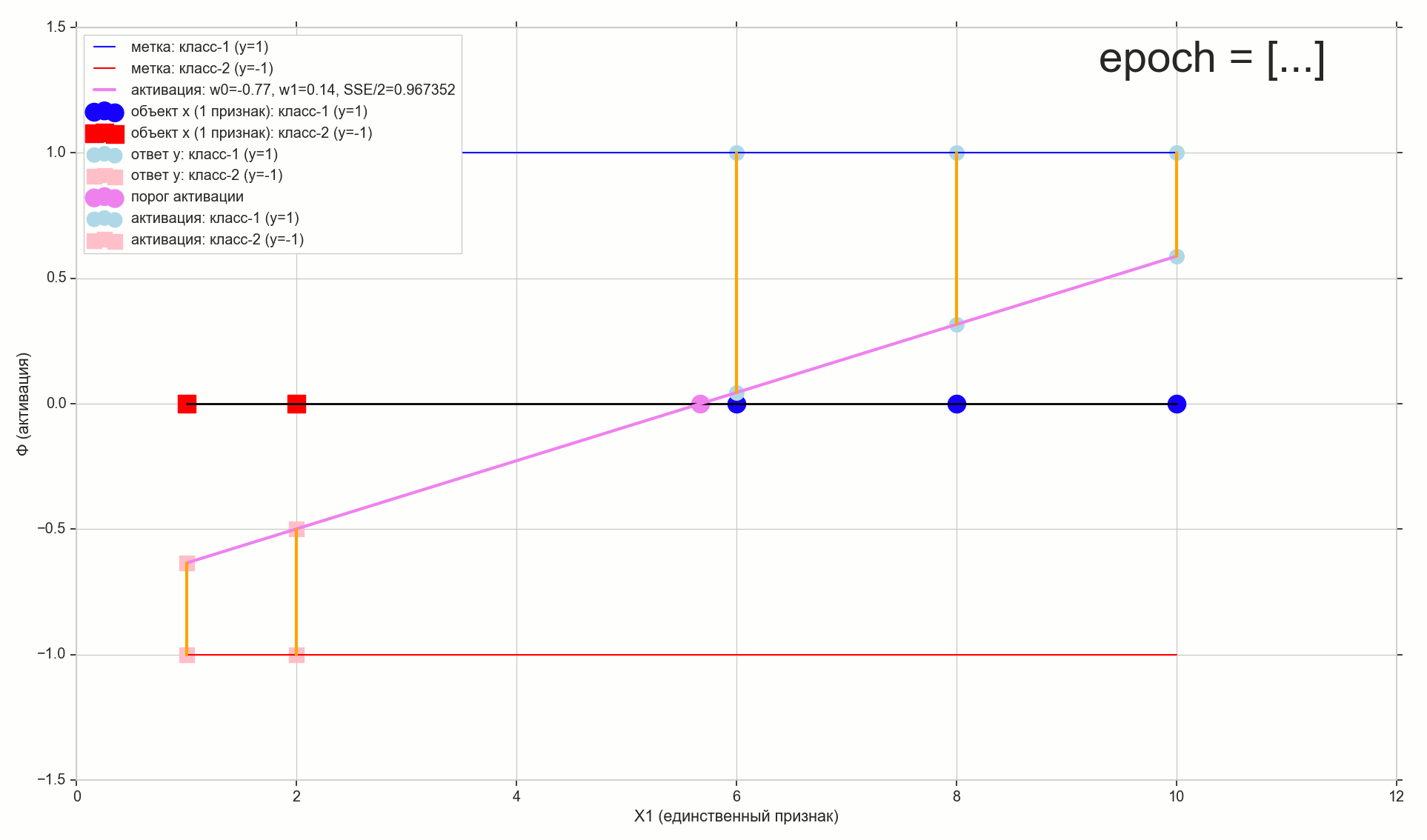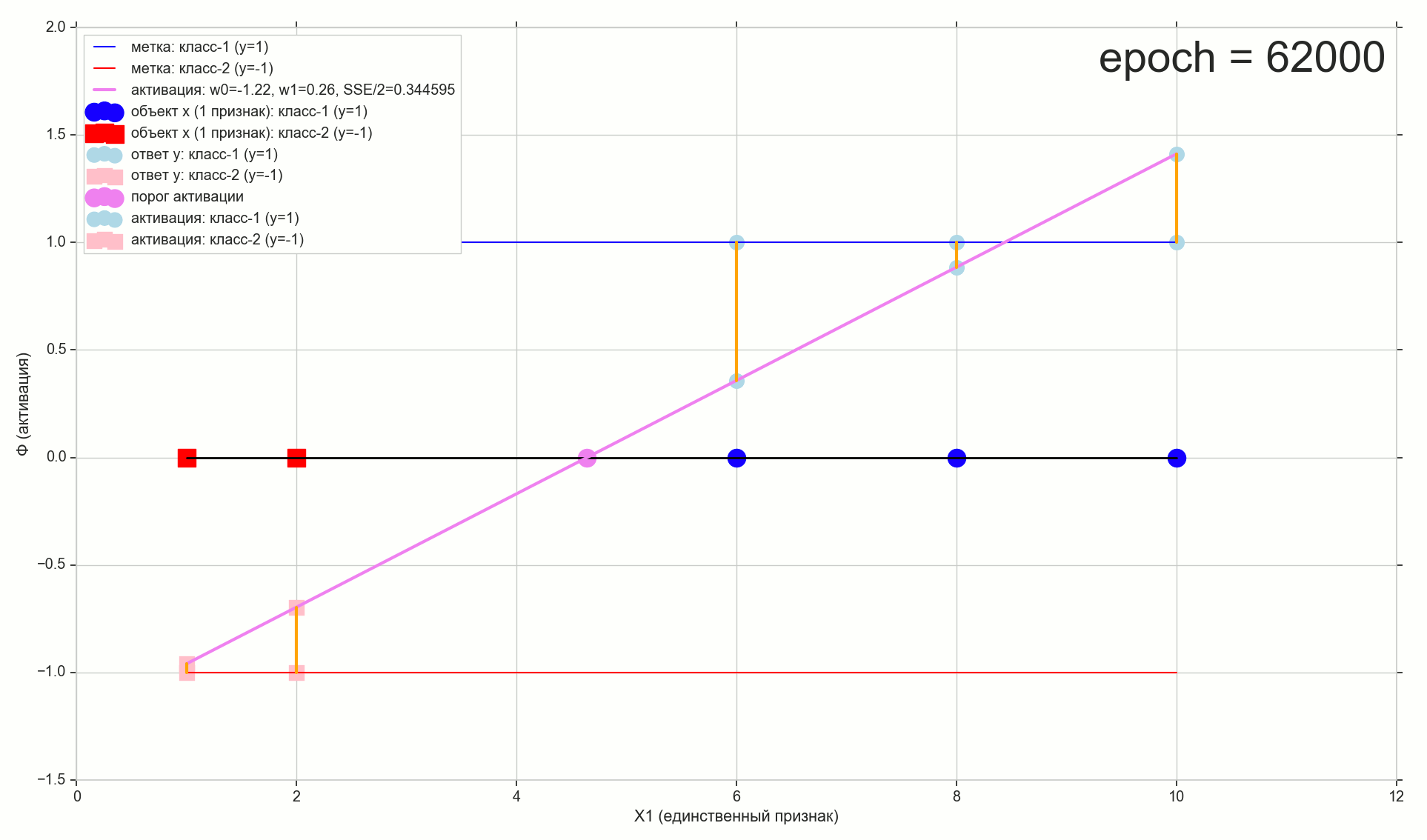
Как стержень на резиночках. Не удивлюсь, если реальная не слишком тяжелая, но жесткая палочка займет такое же положение, если привязать ее к таким же гвоздикам специальными короткими резиночками или пружинками, которые тянутся только по вертикали.
Подытожим
- При на графике сходимости видно, что алгоритм сходится к 10-12-й эпохе (значение ошибки перестает уменьшаться сильно)
- Но, чтобы получить такую же точность, как при ручном поиске минимума по сетке, с таким же коэффициентом нужно отработать почти две тысячи (1767) эпох
- Еще дальше гонять обучение не имеет смысла — ошибка почти не уменьшилась спустя еще 60 тыс эпох
- Нужна ли такая точность или можно довольствоваться еще меньшим — вопрос задачи
Результат обучения — нашли коэффициенты (при условии, что остановились на эпохе 1767): , .
Протестируем наш обученный нейрон.
Возьмем объект с заранее неизвестным классом (будем считать, что — это объекты тестовой выборки). Но, т.к. он находится между двумя красными точками из обучающей выборки, будем ожидать, что обученный нейрон назначит ему класс , т.е. отнесет его к группе красных точек слева.
взвешенная сумма
активация
квантизатор
Как видим, наши ожидания оправдались.
Попробуем еще один вариант:
Это точка находилась между двумя синими точками справа и нейрон назначил ей класс , т.е. отнес ее к группе синих точек справа. Наше мнение и мнение нейрона совпало и в этот раз.
Между прочим, мы с вами только что научили искусственный нейрон (так же известный как мыслящая машина класса «Перцептрон») отличать красные точки слева от синих точек справа и нам потребовалось на это всего 12 попыток. Как по мне, отличный результат!
Двумерное пространство (m=2)
В общем, градиентный спуск, как алгоритм, мы разобрали. Посмотрим еще на вариант с двумерными объектами. Конечно, уже не так подробно, здесь просто есть еще несколько интересных картинок.
Элементы выборки — точки на плоскости (две координаты). Каждый элемент принадлежит к одному из 2-х классов.
- (два признака, а не один, как раньше)
- (как и раньше, классов два)
# точки - признаки (два измерения)
X1 = np.array([2, 3, 1, 5, 10, 1, 6, 7, 10, 6, 7])
X2 = np.array([1, 1, 2, 2, 3, 5, 6, 6, 7, 8, 8])
# метки классов - правильные ответы
y = np.array([-1, -1, -1, -1, 1, -1, 1, 1, 1, 1, 1])plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u'класс: -1')
plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u'класс: 1')
# весовые коэффициенты модели
# вручную - более-менее наглядно
w0 = -2.7
w1 = .3
w2 = .4
# разделяющая линия (порог активации) - пересечение плоскости активации и плоскости Ф=0:
# 0=w0+w1*X1+w2*X2
# X2=-(w0+w1*X1)/w2
plt.plot(np.linspace(0,12), -(w0+w1*np.linspace(0,12))/w2, label=u'порог активации')
plt.xlim(0, 11)
plt.ylim(0, 9)
plt.legend(loc='upper left')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
Здесь могли быть длина и ширина чашелистика ириса, но это просто несколько удобных точек.
Активация
Видим, что у нас активация — это параметрическая плоскость в трёхмерном пространстве, значит мы не можем нарисовать ее на плоскости, как для 1-мерного случая, нужно переходить в 3-д:

Плоскость активации с проекциями элементов:

Плоскости классов с проекциями элементов:

Ошибка для каждого элемента — расстояние от проекции элемента на плоскость активации до проекции этого же элемента на плоскость истинного класса:

Обратите внимание на линию пересечения плоскости активации (сиреневая) и нулевой плоскости (матово-белая). Вот она же на двумерном графике с точками элементов:

В статьях, описывающих градиентный спуск или рассказывающих про нейросети, обычно рисуют такую линию и говорят, что вот ее нам нужно построить, конечно, если множество еще линейно разделимо (оно линейно разделимо, если группы элементов можно разделить вот такой линией). Это правда, но это не вся правда. На самом деле, как мы только что увидели, нам нужно построить не линию в пространстве m=2, а плоскость в пространстве (m+1)=3: пересечение плоскости активации с нулевой координатой активации и даст нам эту линию, хотя все равно одной линии не достаточно — она разделит элементы на две части, но значения классов назначает не линия, а плоскость — в зависимости от того, выше или ниже нуля оказывается проекция элемента на ней (см квантизатор).
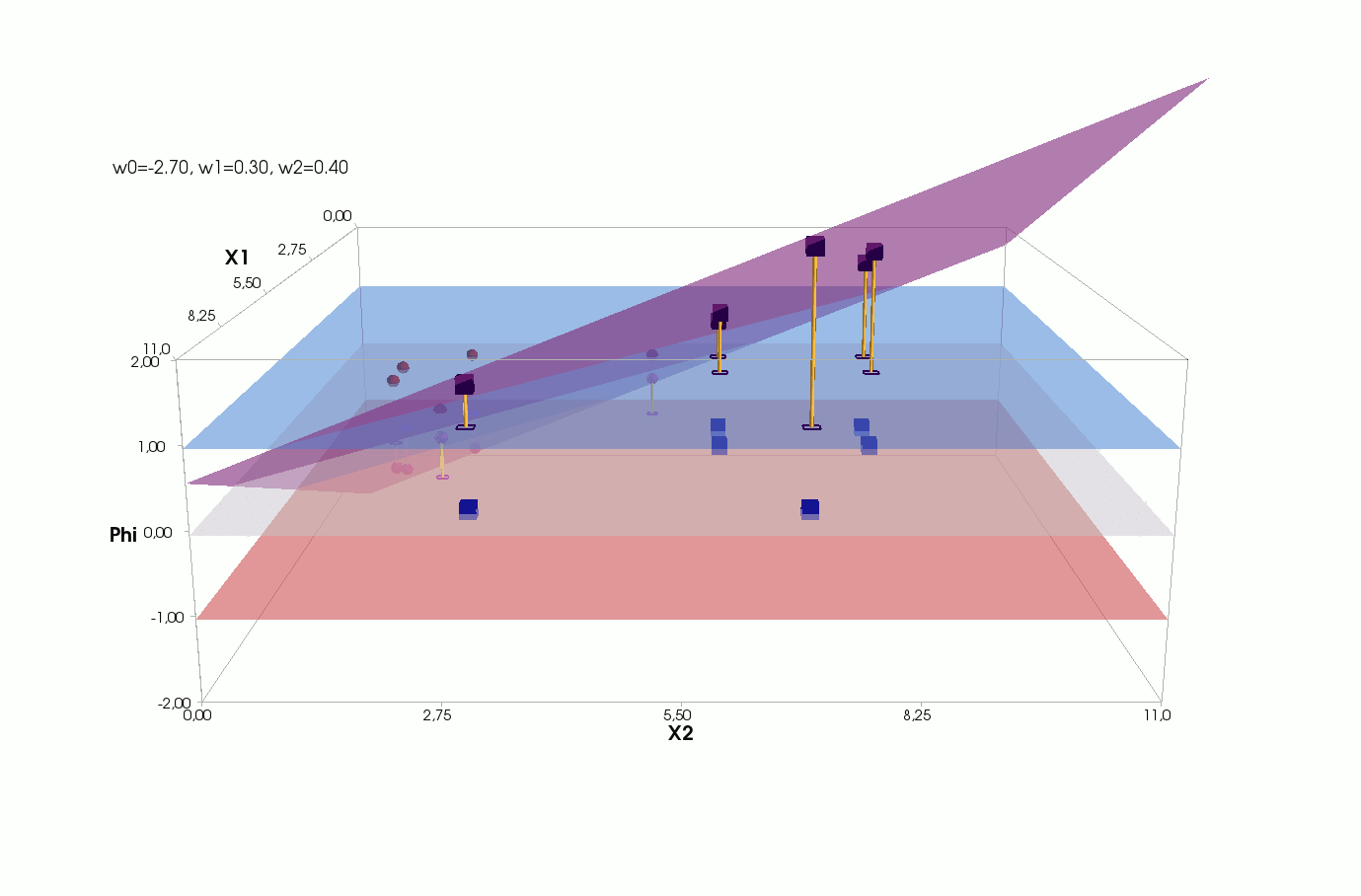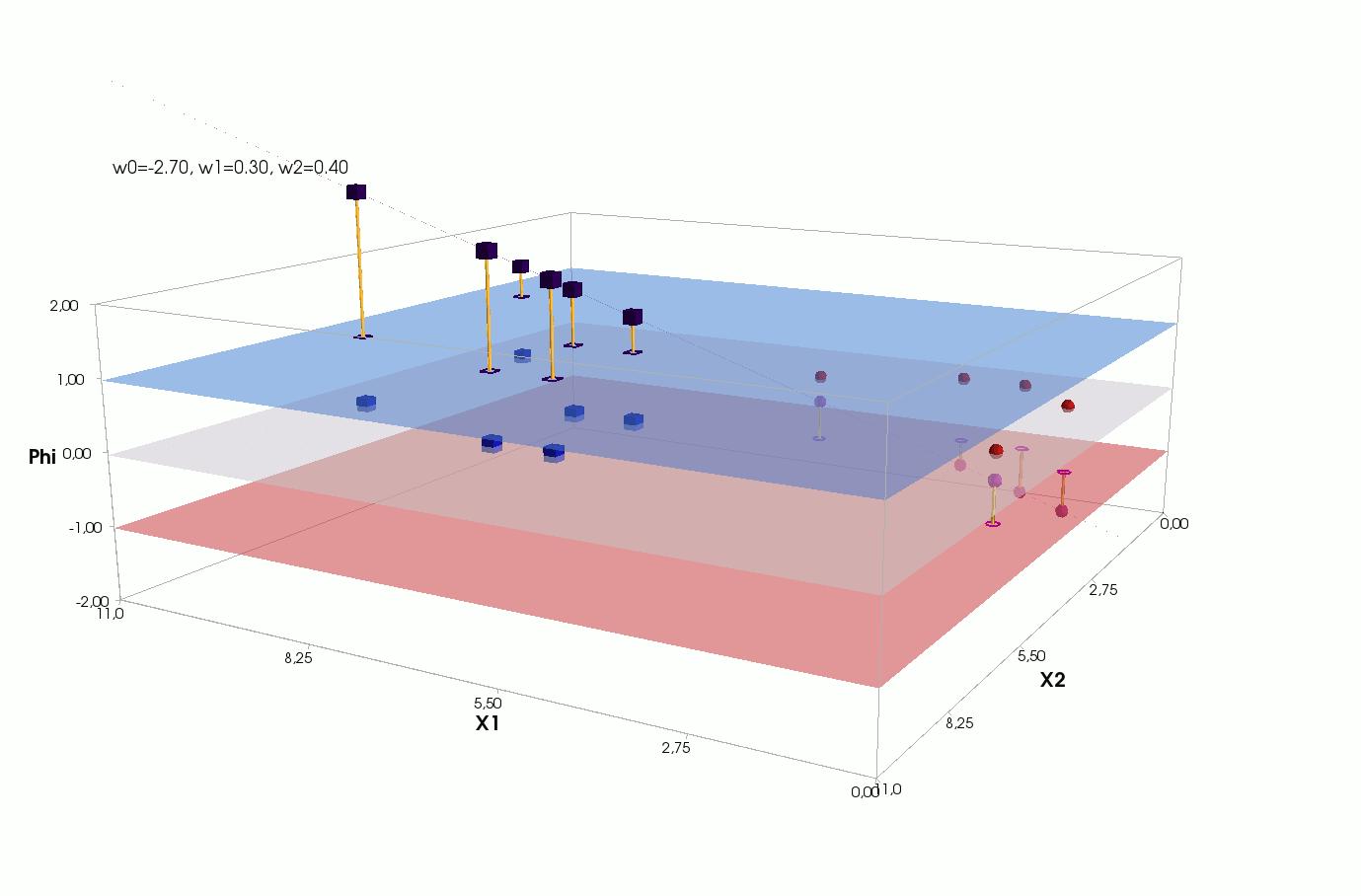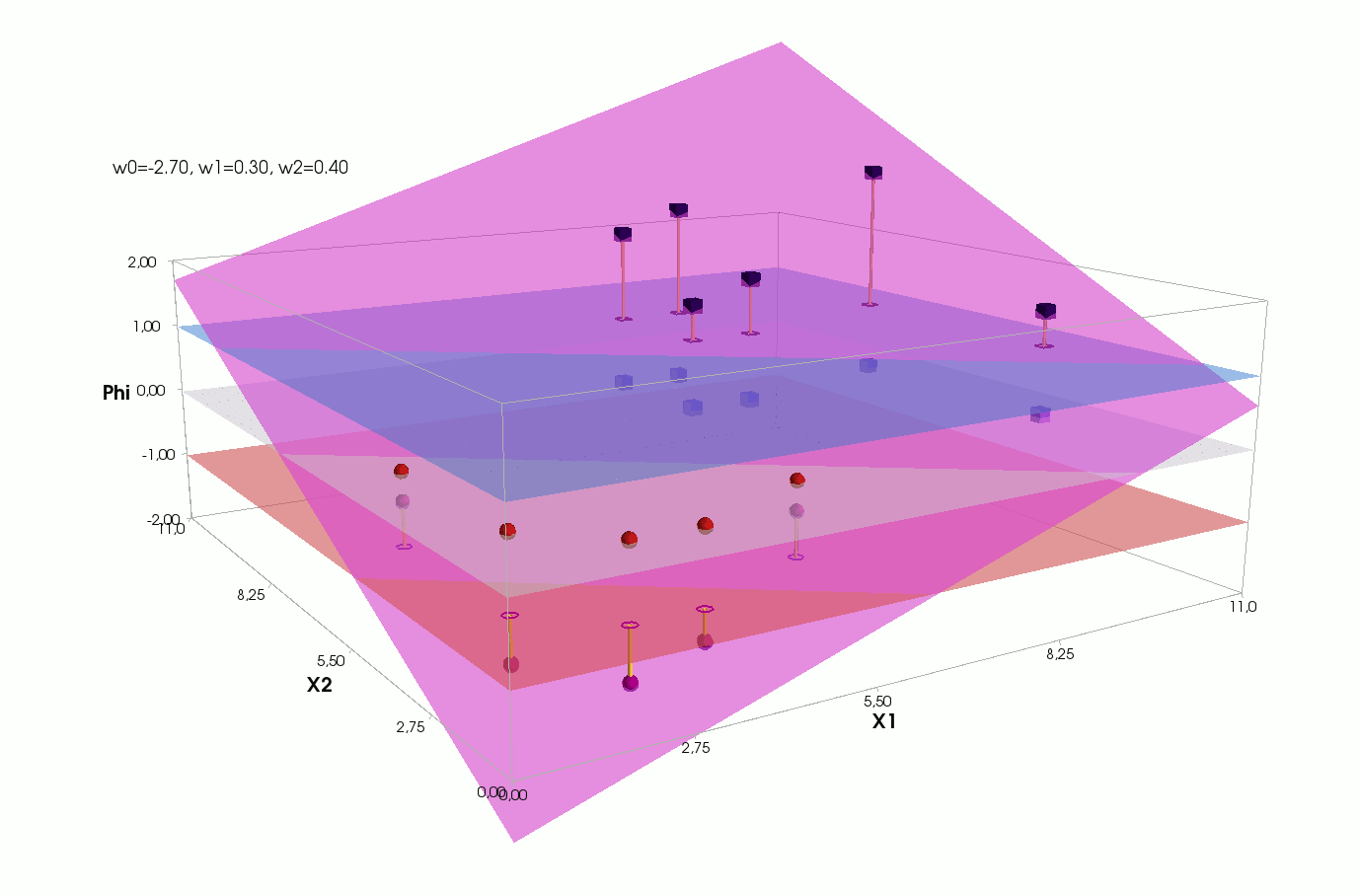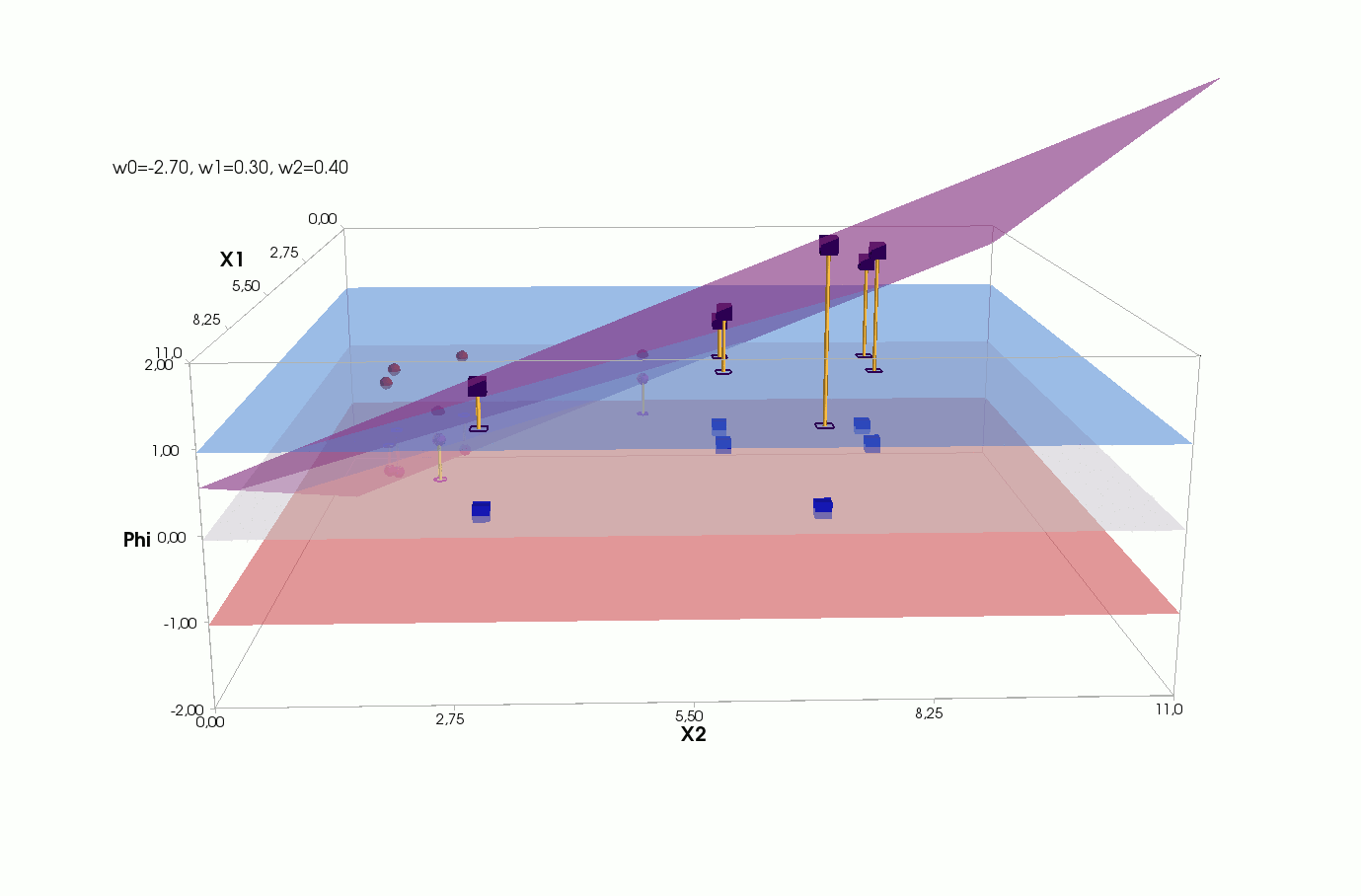
Ошибка
Красивую воронку функции потерь (стоимости) мы здесь нарисовать уже не можем, т.к., как видим, у нас исходных параметра 3 + значение функции — получается 4 измерения. Кому интересно, попробуйте сделать отдельные 2-д или 3-д срезы или придумать что-нибудь с цветовым кодированием нескольких поверхностей на одном 3д-графике, добавить динамику, или воспользоваться какими-нибудь другим приемом изображения 4-мерных поверхностей в 3-д, если вы такие знаете и если они есть.
И это уже для простейшего случая для элементов с 2-мя признаками. Для элементов с большим количеством признаков у впадины будет еще больше измерений, но в нее все равно получится спуститься по градиенту, как в 1-д и как в 2-д.
Спуск по градиенту
Градиент
Частные производные (элементы градиента):
Шаги по каждому из измерений:
Спускаемся одновременно по 3-м параметрам (градиент из 3-х измерений), коэффициент обучения , начальные значения небольшие фиксированные , , .
Начальная позиция — плоскость активации, зацепившись уголком за вертикальную ось на краю видимой области, свисает далеко вниз:


Уже на первом шаге стремительно подлетает вверх:

Крышка захлопнулась:

К 3-му шагу линия пересечения активации с нулевой плоскостью элементов уже проходит плюс-минус сквозь группы элементов:

На 4-м шаге она назначает неправильный класс только одному красному элементу:

На 60-м шаге положение еще не поменялось — плоскость активации постепенно доворачивается, но с неправильным классом остался все тот же один красный элемент:

Примерно к 70-му шагу он, наконец, тоже попал в свою группу:

Шаг 200-й — все элементы по своим группам с некоторым запасом:

Шаг 400-й — радикальных изменений уже нет:

В динамике:

Здесь интересно наблюдать, как плоскость активации стремительно подлетает наверх по всем параметрам одновременно, а потом начинает всё медленнее доворачиваться почти только по .
Код
Библиотека matplotlib (её расширение mpl_toolkits.mplot3d.axis3d) не умеет в пересекающиеся поверхности (все приведенные выше графики можно построить, но они будут выглядеть, как плохо читабельная каша в антураже 3д). Поэтому для построения красивых трёхмерных графиков выше мы воспользовались замечательной библиотекой Mayavi.
import numpy
from mayavi import mlab
# не показывать окно - для режима mlab.savefig
#mlab.options.offscreen = True
# здесь нужен size для нормальной работы mlab.savefig
fig = mlab.figure(fgcolor=(10./256., 10./256., 10./256.),
bgcolor=(255./256., 255./256., 255./256.), size=(1650, 950))
X1_ = range(0, 12)
X2_ = range(0, 12)
XX1_, XX2_ = np.mgrid[X1_, X2_]
# Палитра из Блендера
# оранжевый: color=(255./256., 191./256., 71./256.)
# бордовый: color=(171./256., 0./256., 130./256.)
# красный: color=(255./256., 101./256., 107./256.)
# розовый: color=(252./256., 79./256., 245./256.)
# голубой: color=(84./256., 148./256., 247./256.)
# фиолетовый: color=(45./256., 0./256., 82./256.)
# желтый: color=(254./256., 255./256., 87./256.)
# Яркие
# красный: color=(.7, .1, .1)
# синий: color=(.1, .1, .7)
# горизонтальные плоскости меток: Ф=1 (y=1), Ф=-1 (y=-1) и нулевая плоскость Ф=0
mlab.surf(XX1_, XX2_, np.full((12, 12), -1),
color=(255./256., 101./256., 107./256.), opacity=0.6)
mlab.surf(XX1_, XX2_, np.full((12, 12), 1),
color=(84./256., 148./256., 247./256.), opacity=0.5)
mlab.surf(XX1_, XX2_, np.full((12, 12), 0),
color=(247./256., 243./256., 246./256.), opacity=0.5)
# точки на нулевой плоскости
# (их тоже нужно нарисовать, т.к. искомая плоскость должна разделить именно их, а не
# их проекции на плоскостях меток: мы работаем в 2-мерном пространстве, 3е измерение -
# измерение функции активации, включаещее метки классов)
mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, 0),
color=(.7, .1, .1), mode='sphere', scale_factor=.2)
mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 0),
color=(.1, .1, .7), mode='cube', scale_factor=.2)
# точки на плоскостях меток
mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, -1),
color=(171./256., 0./256., 130./256.), mode='2dcircle', scale_factor=.2)
mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 1),
color=(45./256., 0./256., 82./256.), mode='2dsquare', scale_factor=.2)
# весовые коэффициенты модели
# Спуск по градиенту по эпохам
# ...
epoch=12
w0=-0.762718
w1=0.165023
w2=0.040271
sse=3.598883
# активация - разделяющая плоскость y=w0+w1*X1+w2*X2
yy_ = w0 + w1*XX1_ + w2*XX2_
actsurf = mlab.surf(XX1_, XX2_, yy_, color=(252./256., 79./256., 245./256.), opacity = 0.6)
# проекции обучающих точек на плоскость активации
y_ = w0 + w1*X1 + w2*X2
mlab.points3d(X1[y==-1], X2[y==-1], y_[y==-1],
color=(171./256., 0./256., 130./256.), mode='sphere', scale_factor=.2)
mlab.points3d(X1[y==1], X2[y==1], y_[y==1],
color=(45./256., 0./256., 82./256.), mode='cube', scale_factor=.2)
# линии ошибок - расстояния от точек на плоскости активации
# до горизонтальных плоскостей меток классов
for i in range(len(X1[y==-1])):
mlab.plot3d(
[X1[y==-1][i], X1[y==-1][i]],
[X2[y==-1][i], X2[y==-1][i]],
[y[y==-1][i], y_[y==-1][i]],
color=(255./256., 191./256., 71./256.))
for i in range(len(X1[y==1])):
mlab.plot3d(
[X1[y==1][i], X1[y==1][i]],
[X2[y==1][i], X2[y==1][i]],
[y[y==1][i], y_[y==1][i]],
color=(255./256., 191./256., 71./256.))
# область видимости - на нее будем насаживать оси координат
# (координатам обязательно нужен объект на рабочем поле)
zmin=-2.
zmax=2.
vis_area = mlab.points3d(
[np.min(X1_), np.max(X1_)],
[np.min(X2_), np.max(X2_)],
[zmin, zmax],
mode='point')
# установить камеру с центром вращения в геометрическом центре графика
mlab.view(
focalpoint=((np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2),
distance=25, azimuth=-50, elevation=75)
mlab.move((0,0,10))
# без этого у пересекающихся поверхностей не будет видно линий пересечений
fig.scene.renderer.use_depth_peeling = 1
# оси
mlab.outline(vis_area, color=(.7, .7, .7))
# здесь пять меток, чтобы было аккуратно на вертикальной оси: -2, -1, 0, 1, 2
axes = mlab.axes(vis_area, nb_labels=5, color=(.7, .7, .7),
ranges=[np.min(X1_), np.max(X1_), np.min(X2_), np.max(X2_), zmin, zmax],
#xlabel=u'X1', ylabel=u'X2', zlabel=u'Ф(SUM) - активация')
xlabel=u'X1', ylabel=u'X2', zlabel=u'Phi') # юникод здесь тоже не работает
#from pprint import pprint
#pprint(vars(axes))
axes._label_text_property.bold = False
axes._label_text_property.italic = False
axes._title_text_property.bold = True
axes._title_text_property.italic = False
# свойство есть, но оно не работает
#axes._title_text_property.font_size = 34
# размер шрифтов для шкалы и меток осей регулируем так:
axes.axes.font_factor = .7
# заголовок раскосопиздит при масштабировании с параметром size в mlab.figure,
# если не задать ему здесь вручную размер
title = mlab.title("epoch=" + str(epoch))
title.actor.text_scale_mode='none'
title.property.justification='right'
title.property.font_size=48
legend = mlab.text(.6, .8, 'w0=%0.2f, w1=%0.2f, w2=%0.2f, sse/2=%0.6f'%(w0, w1, w2, sse/2))
legend.actor.text_scale_mode='none'
legend.property.font_size=18
# показать окно
mlab.show()
# сохранить в файл
#mlab.savefig("epoch" + str(epoch) + ".png")
# для вызова в цикле: дадим файлу сохраниться перед тем, как очищать ресурсы
# (так делать не очень красиво, правильнее, конечно, не убивать,
# а очищать рабочую область, но здесь ок и так)
#mlab.clf()
#mlab.close()
# вращение вокруг центра - посмотреть активацию со всех сторон
'''
fpoint = ( (np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2 )
for i in range (0, 360, 2):
mlab.view(focalpoint=fpoint, distance=25, elevation=75,
azimuth=i)
mlab.move((0,0,10))
mlab.savefig("act-2d-azimuth" + str(i) + ".png")
'''Тот факт, что Mayavi является глючной инопланетянской поделкой, нисколько не отменяет заложенный в неё потенциал нереальной мощщи. Часы и нервы, потраченные во время её первичной установки, а потом освоения, в конечном итоге стоят того.
Mayavi, в отличие от Matplotlib/axes3d, использует на 3д-сцене полноценный OpenGL. Однако, он будет работать нормально (рисовать пересекающиеся плоскости) только в том случае, если использовать с ним бэкэнд для рендера на основе Qt. По умолчанию этот бэкэнд вместе с mayavi не устанавливается и не включается. Я установил через pip пакеты PyQt5 и python-qt (возможно, еще какие-то пакеты, содержащие в имени строку 'qt'). Честно, не знаю, какой из них сработал, но в конечном итоге у меня получилось успешно запустить скрипт, корректно рисующий пересекающиеся плоскости, вот так:
env QT_API=pyqt python3 gradient-2d.pyСходимость по эпохам — график спуска стоимости вниз по шагам
def sse_(X1, X2, y, w0, w1, w2):
return ((w0+w1*X1+w2*X2 - y)**2).sum()
# спускаемся по градиенту к минимуму J(w0, w1, w2)
# одновременно по w0, w1 и w2
# норм спуск
eta = 0.001
# у всех точек правильные классы (впритык)
epochs = 70
w0_first = -.9
w1_first = -.9
w2_first = -.9
# спуск по точкам по градиенту
w0_epochs = [w0_first]
w1_epochs = [w1_first]
w2_epochs = [w2_first]
delta_w0_epochs = []
delta_w1_epochs = []
delta_w2_epochs = []
w0_next = w0_first
w1_next = w1_first
w2_next = w2_first
for i in range(epochs):
grad_w0 = (w0_next + w1_next*X1 + w2_next*X2 - y).sum()
delta_w0 = -eta*grad_w0
grad_w1 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X1).sum()
delta_w1 = -eta*grad_w1
grad_w2 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X2).sum()
delta_w2 = -eta*grad_w2
w0_next = w0_next + delta_w0
w1_next = w1_next + delta_w1
w2_next = w2_next + delta_w2
delta_w0_epochs.append(delta_w0)
delta_w1_epochs.append(delta_w1)
delta_w2_epochs.append(delta_w2)
w0_epochs.append(w0_next)
w1_epochs.append(w1_next)
w2_epochs.append(w2_next)
# квадратичные ошибки по эпохам
sse_epochs = []
for i in range(len(w1_epochs)):
sse = sse_(X1, X2, y, w0_epochs[i], w1_epochs[i], w2_epochs[i])
sse_epochs.append(sse)
#print('epoch=%d, w0=%f, w1=%f, w2=%f, SSE=%f, SSE/2=%f' %
# (i, w0_epochs[i], w1_epochs[i], w2_epochs[i], sse, sse/2))
sse_epochs = np.array(sse_epochs)
# график - ошибка от эпохи при выбранном ? (-эта-)
plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, ?=%s'%eta)
plt.xlabel(u'epoch (?=%s)'%eta)
plt.ylabel(u'J(w)')
plt.legend(loc='upper right')
plt.show()12 эпох:

70 эпох:

Здесь отметим, что из этих графиков уже не очень понятно, в какой момент нужно останавливаться: ошибка радикально падает уже к 6-12-й эпохе, а полностью корректная классификация всех точек обучающей выборки наступает только в районе 70-го шага — почему стоит остановиться именно на 70-м шаге, а не на 30-м, 40-м или 200-м, этот график, по крайней мере, в представленном виде, ответ не дает.
Заключение
Архитектура ADALINE (adaptive linear neuron — адаптивный линейный нейрон) — искусственный нейрон с линейной функцией активации на текущий момент считается устаревшей. Разработчики библиотеки scikit-learn не хотят включать алгоритм ADALINE (вариант в веб-архиве для тех, у кого роскомнадзор) в свою библиотеку, ссылаясь на то, что они предпочитают не тратить время и силы на поддержку ретро-алгоритмов «из 80-х» (ADALINE из 60-х), которые для решения современных практических задач больше никому не нужны.
Автор замечательной книги «Python и машинное обучение» Себастьян Рашка (он же начал приведенное выше обсуждение в рассылке разработчиков scikit-learn) приводит свою реализацию алгоритма в бумажной книге, онлайн-версии книги и на гитхабе в образовательных целях и в качестве музейного экспоната.
Но мы с вами провели всё это время с нейроном ADALINE не зря.
Во-первых, линейная активация — отличная подопытная функция для изучения алгоритма градиентного спуска, который используется и с другими вариантами активаций: устарела конкретная комбинация нейрона и линейной активации, но сам нейрон и метод его обучения градиентным спуском, тем более, сам алгоритм градиентного спуска никак не устарел.
Во-вторых, если мы отрежем от нашего нейрона порог (квантизатор) так, что на выходе будет не двоичная метка класса, а значение активации на непрерывной шкале, мы вместо нейрона получим алгоритм построения линейной регрессии в чистом виде (значение активации будет значением целевой переменной, да, в качестве истинных значений тоже вместо меток взять непрерывные значения) — это вполне себе актуальный метод машинного обучения, реализация которого присутствует в том числе в библиотеке scikit-learn.
P.S. У меня так сходу не получилось проследить, чем отличается нейрон ADALINE от перцептрона Розенблатта с линейной функцией активации и отличаются ли они вообще. Перцептрон Розенблатта по времени появился раньше, архитектурно, судя по описанию, они идентичны, но в статьях про ADALINE почему-то не ссылаются на Розенблатта, а ссылаются на других людей. Поэтому здесь я осторожно предполагаю, что ADALINE можно считать специальным названием для единичного перцептрона Розенблатта с линейной функцией активации. Возможно, кто-то в комментариях сможет этот момент прояснить.
Комментарии (12)

slavos1sss
22.10.2019 01:34Я подобного математического шедевра еще не видел. В хорошем смысле. Очень круто! ))

mayorovp
22.10.2019 09:36P.S. У меня так сходу не получилось проследить, чем отличается нейрон ADALINE от перцептрона Розенблатта с линейной функцией активации и отличаются ли они вообще.
Насколько я помню, нейрон ADALINE от перцептрона Розенблатта отличается тем, что в перцептроне есть дополнительный случайный необучаемый слой с нелинейной функцией активации. То есть анализируются не входные признаки, а их случайные комбинации. И есть теорема, которая утверждает что любое множество точек станет линейно разделимым если "накидать" достаточное число нейронов в промежуточном слое.

sadr0b0t Автор
22.10.2019 13:14Да, перцептроном Розенблатта обычно называют многослойную структуру с нелинейной активацией, но в литературе, когда начинают рассказывать про нейросетки, повсеместно говорят об однослойном перцептроне, который по сути есть единичный нейрон.

mayorovp
22.10.2019 13:30Так я как раз про "однослойный" перцептрон и писал. Слово "однослойный" в кавычках потому что у него всё равно два слоя, просто только один слой обучаемый.

mgoffeeyv
22.10.2019 13:11Как такое сделать на JS?

sadr0b0t Автор
22.10.2019 13:18+2Код здесь приведен в учебных целях для наглядности. Для практических применений лучше взять какую-нибудь готовую библиотеку с реализацией нейросетки, должно быть что-то и для JS.
Если хотите строить на JS такие же графики, то не знаю, возможно и для JS есть что-то подобное, но, вообще, именно за такие графики и манипулирование многомерными массивами многие любят как раз Пайтон.

Costic
22.10.2019 16:44Статья мощная, фундаментальная. Не знаю, сможет ли человек без подготовки, который «не в теме», разобраться в её содержимом. Математические основы изложенного метода лет 60 как хорошо описаны. И за эти годы продвинулись вперёд, особенно с появлением мощных ЭВМ. Я бы интересующимся этой темой рекомендовал читать «Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий, 1971» или более свежую «Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: учебное пособие, 1999 (2002)». Последняя книжка отсканирована и доступна. Там и градиент, и тяжёлый шарик, и случайный поиск и много всего.
Я тоже занимался подобной тематикой, только называлось это не нейросети, а моделирование, прогнозирование, оптимизация. Сначала я встроил чужой компонент (ActiveX). Выглядело примерно вот так: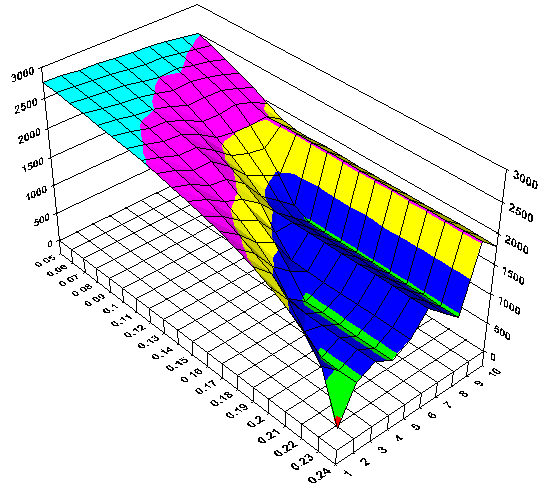
Но этого оказалось недостаточно и появилось такое чудо:
Которое было анимировано:
Это из моих публикаций 1999 года.

SergeySib
22.10.2019 18:32Автор, спасибо за статью! Хабр торт :)
Я давно не следил за прогрессом в нейросетях, потому задам несколько празндых вопросов не совсем по теме статьи:
1) Современные нейросети глубинного обучения построены на таких же нейронах (быть может, с более хитрой функцикей активации), или на чём-то принципиально ином?
2) Насколько я знаю, современные нейросети многослойны. Чем отличается нейрон многослойной сети от нейрона однослойной сети? Отсутствием пороговой функции?
3) Какие методы оптимизации используются в машинном обучении на практике? Такой же градиентный спуск?
CheY
22.10.2019 20:171) В первом приближении таких же. Разве что функция суммации может быть изощренней из-за тех же свёрток, например. И да, чем глубже сеть, тем больше внимания уделяют функциям активации, наряду с другими ухищрениями (архитектурой, регуляризацией, инициализацией весов, нормировкой выходов слоёв и т.д.), чтобы обеспечить стабильную работу градиентного спуска.
2) Ничем. Многослойность говорит только о том, сколько слоёв нейронов соединены друг с другом.
3) Да, градиентные методы остаются наиболее универсальными. Разумеется у них много вариаций и улучшений по сравнению с самым наивным вариантом, но суть остаётся той же.
malkovsky
23.10.2019 17:25По 3) есть один важный момент: на самом деле в ML используются стохастический градиентный спуск и его модификации, обычный градиентный спуск в ML бесполезен. Просто оказывается гораздо эффективней разбить данные скажем на 100 частей и сделать 100 итераций градиентного спуска учитывая на каждом шаге только одну часть нежели сделать одну итерацию на всех данных. В обоих случаях вычислительные затраты практически идентичны.


Norsat
Да уж.
А реальный нейрон просто возбуждается, не зная про весь этот математический и вычислительный ужас.
Просмотрев пост, хочется стать нейроном.