В геймдеве часто нужно что-нибудь завязать на рандоме: у Unity для этого есть свой Random, а параллельно с ним существует System.Random. Когда-то давно на одном из проектов сложилось впечатление, что оба могут работать по-разному (хотя должны иметь равномерное распределение).

Тогда в детали углубляться не стали — хватило того, что переход на System.Random исправил все проблемы. Сейчас решили разобраться подробнее и провести небольшое исследование: насколько «предвзяты» или предсказуемы ГСЧ, и какой выбрать. Тем более, я не раз слышал противоречивые мнения об их «честности» — попробуем разобраться, как реальные результаты соотносятся с заявленными.

Краткий ликбез или ГСЧ это на самом деле ГПСЧ

Если вы уже знакомы с генераторами случайных чисел, то можете сразу переходить к разделу «Тестирование».

Случайные числа (СЧ) — это последовательность чисел, генерируемая с помощью некоторого случайного (хаотического) процесса, источника энтропии. То есть это такая последовательность, элементы которой не связаны между собой каким-либо математическим законом — у них отсутствует причинно-следственная связь.

То, что создает СЧ называется генератором случайных чисел (ГСЧ). Казалось бы, все элементарно, но если от теории перейти к практике, то на самом деле реализовать программный алгоритм генерации такой последовательности не так просто.

Причина кроется в отсутствии той самой хаотичности в современной потребительской электронике. Без нее случайные числа перестают быть случайными, а их генератор превращается в обычную функцию от заведомо определенных аргументов. Для целого ряда специальностей в IT-сфере это серьезная проблема (например, для криптографии), для остальных же есть вполне допустимое решение.

Нужно написать алгоритм, который возвращал бы пусть и не истинно случайные числа, но максимально приближенные к ним — так называемые, псевдослучайные числа (ПСЧ). Алгоритм в этом случае называется генератором псевдослучайных чисел (ГПСЧ).

Есть несколько вариантов создания ГПСЧ, но для всех будет актуально следующее:

1. Необходимость предварительной инициализации.
   
   ГПСЧ лишен источника энтропии, поэтому перед использованием ему необходимо указать начальное состояние. Оно задается в виде числа (либо вектора) и называется зерном (seed, random seed). Нередко в качестве seed используется счетчик тактов процессора или числовой эквивалент системного времени.
2. Воспроизводимость последовательности.
   
   ГПСЧ является полностью детерминированным, поэтому заданный при инициализации seed однозначно определяет всю будущую последовательность чисел. Это значит, что отдельно взятый ГПСЧ, проинициализированный одинаковым seed (в разное время, в разных программах, на разных устройствах) будет генерировать одну и ту же последовательность.

Еще нужно знать характеризующее ГПСЧ распределение вероятностей — какие числа он будет генерировать и с какой вероятностью. Чаще всего это либо нормальное распределение (normal distribution), либо равномерное распределение (uniform distribution).

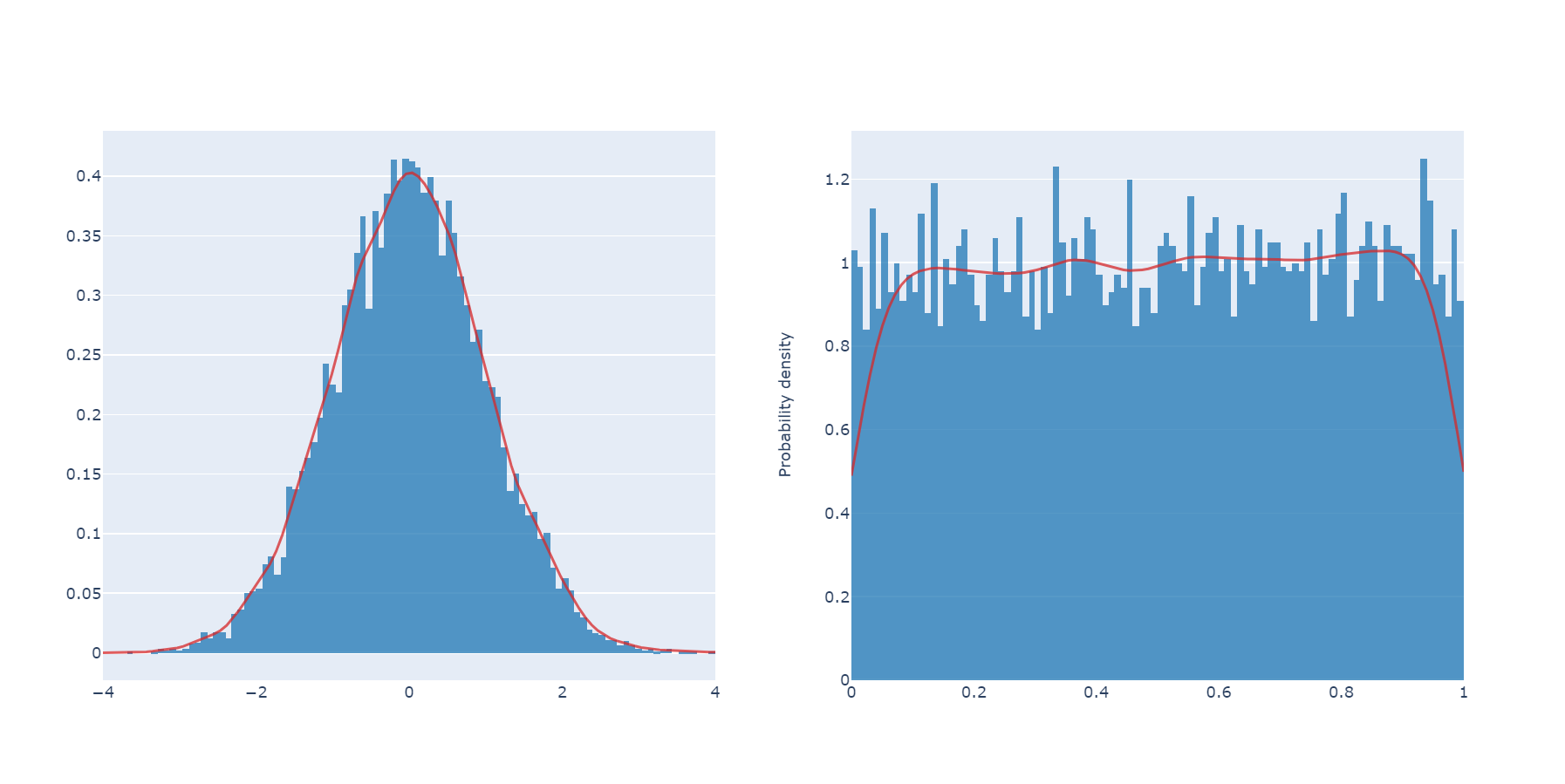
Нормальное распределение (слева) и равномерное распределение (справа)

Допустим, у нас есть честная игральная кость с 24 гранями. Если ее подбросить, то вероятность выпадения единицы будет равна 1/24 (как и вероятность выпадения любого другого числа). Если совершить множество бросков и записывать результаты, то можно заметить, что все грани выпадают примерно с одной и той же частотой. По сути эту игральную кость можно считать ГСЧ с равномерным распределением.

А если подбрасывать сразу 10 таких костей и считать общую сумму очков? Будет ли для неё сохраняться равномерность? Нет. Чаще всего сумма будет близка к 125 очкам, то есть к некоторому среднему значению. И как следствие — еще до совершения броска можно примерно оценить будущий результат.

Причина в том, что для получения средней суммы очков существует наибольшее количество комбинаций. Чем дальше от нее, тем меньше комбинаций — и соответственно, меньше вероятность выпадения. Если эти данные визуализировать, то они будут отдаленно напоминать форму колокола. Поэтому с некоторой натяжкой систему из 10 костей можно назвать ГСЧ с нормальным распределением.

Еще один пример, только уже в плоскости — стрельба по мишени. Стрелком будет ГСЧ, генерирующий пару чисел (x, y), которая отображается на графике.

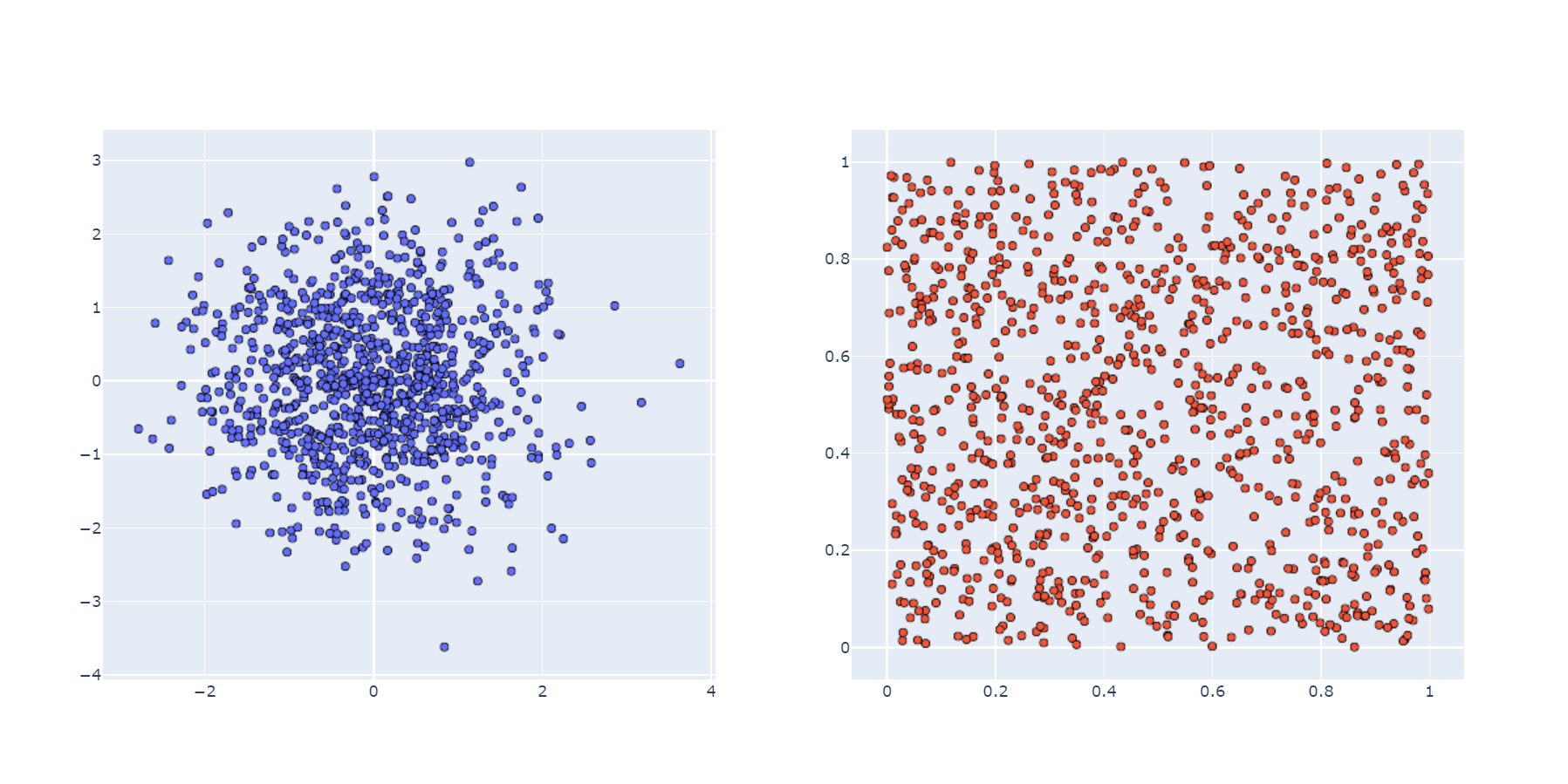
Согласитесь, что вариант слева более приближен к реальной жизни — это ГСЧ с нормальным распределением. Но если нужно разбросать звезды на темном небе, то лучше подойдет правый вариант, полученный с помощью ГСЧ с равномерным распределением. В общем, выбирайте генератор в зависимости от поставленной задачи.

Теперь поговорим про энтропию последовательности ПСЧ. Например, есть последовательность, которая начинается так:

89, 93, 33, 32, 82, 21, 4, 42, 11, 8, 60, 95, 53, 30, 42, 19, 34, 35, 62, 23, 44, 38, 74, 36, 52, 18, 58, 79, 65, 45, 99, 90, 82, 20, 41, 13, 88, 76, 82, 24, 5, 54, 72, 19, 80, 2, 74, 36, 71, 9, …

Насколько эти числа случайны на первый взгляд? Начнем с проверки распределения.

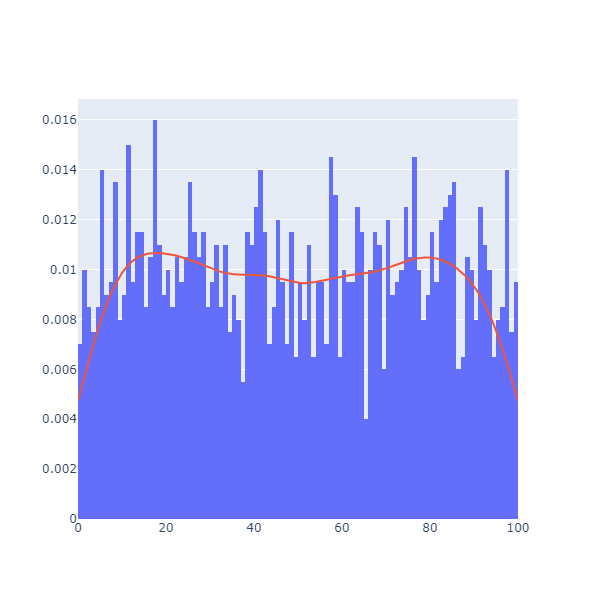
Выглядит как близкое к равномерному, но если считывать последовательность по два числа и интерпретировать их как координаты на плоскости, то получится это:

Становятся отчетливо видны паттерны. А раз данные в последовательности определенным образом упорядочены (то есть обладают низкой энтропией), то это может порождать ту самую «предвзятость». Как минимум, такой ГПСЧ не очень то подходит для генерации координат на плоскости.

Другая последовательность:

42, 72, 17, 0, 30, 0, 15, 9, 47, 19, 35, 86, 40, 54, 97, 42, 69, 19, 20, 88, 4, 3, 67, 27, 42, 56, 17, 14, 20, 40, 80, 97, 1, 31, 69, 13, 88, 89, 76, 9, 4, 85, 17, 88, 70, 10, 42, 98, 96, 53, …

Вроде бы тут все хорошо даже на плоскости:

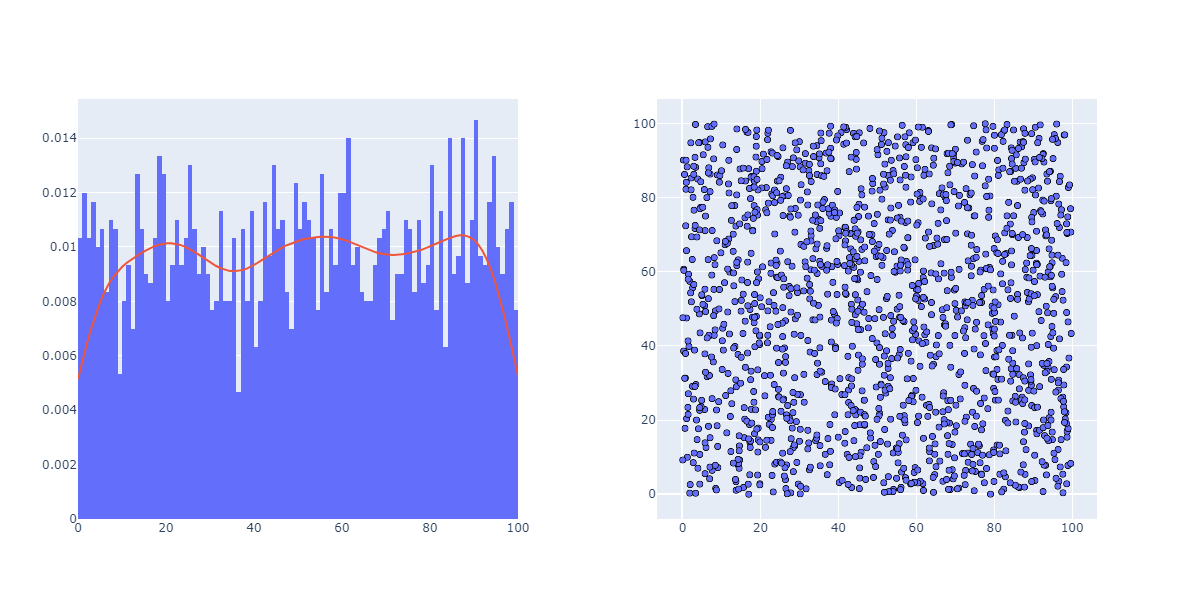
Посмотрим в объеме (считываем по три числа):

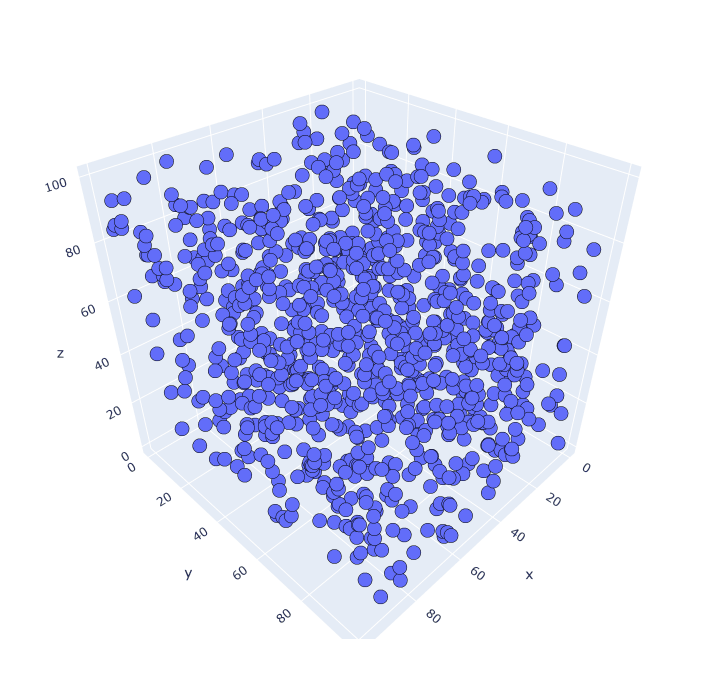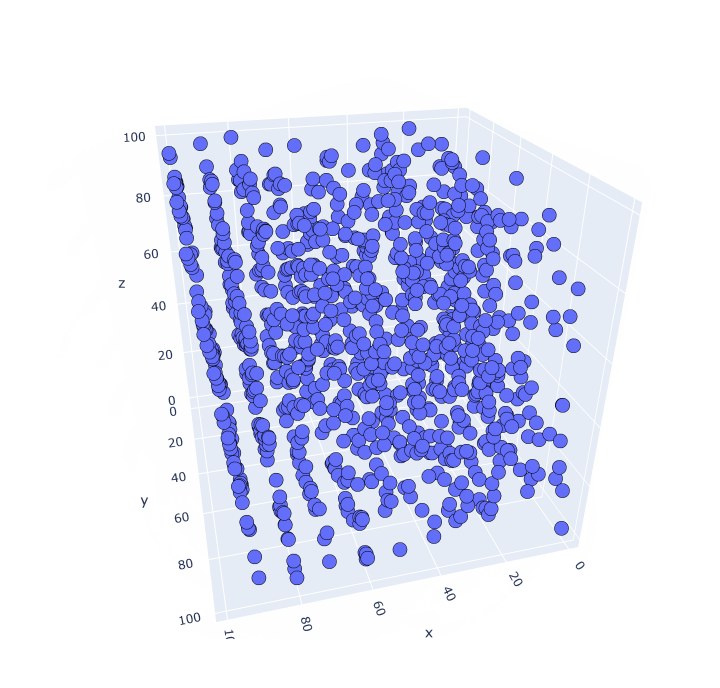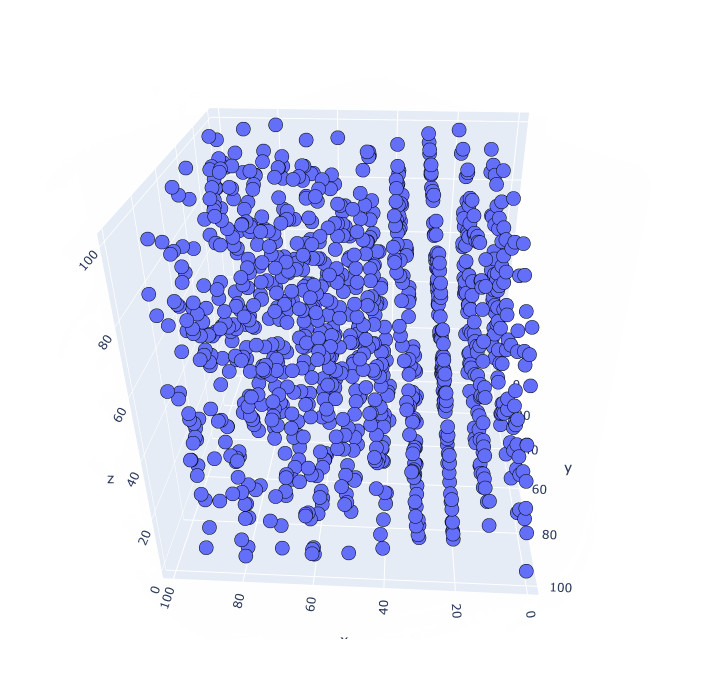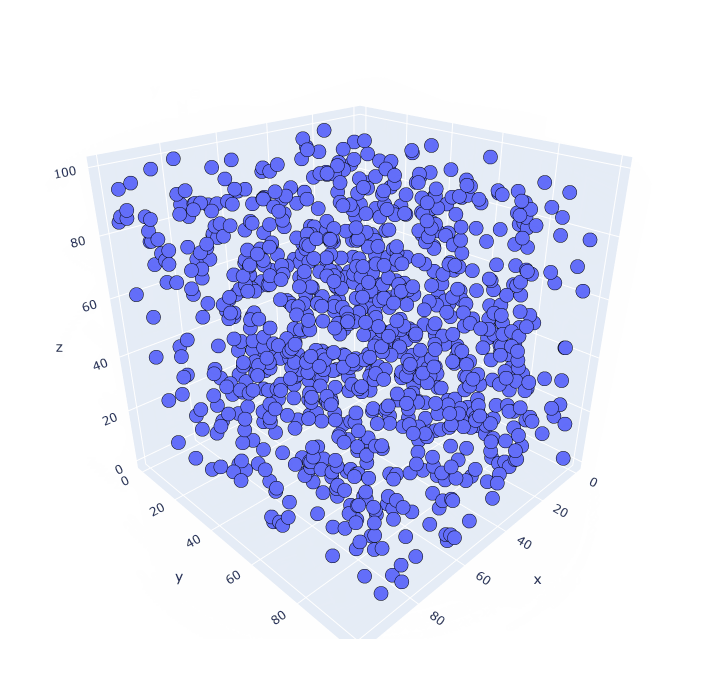
И снова паттерны. Построить визуализацию в четырех измерениях уже не получится. Но паттерны могут существовать и на этой размерности, и на больших.

В той же криптографии, где к ГПСЧ предъявляются самые жесткие требования, подобная ситуация категорически недопустима. Поэтому для оценки их качества разработаны специальные алгоритмы, касаться которых мы сейчас не будем. Тема обширная и тянет на отдельную статью.

Тестирование

Если мы чего-то не знаем наверняка, то как с этим работать? Стоит ли переходить дорогу, если ты не знаешь какой сигнал светофора это разрешает? Последствия могут быть разные.

То же самое касается пресловутого рандома в Unity. Хорошо, если документация раскрывает необходимые подробности, но упомянутая в начале статьи история произошла как раз из-за отсутствия желанной конкретики.

А не зная, как работает инструмент, не сможешь его корректно применить. В общем, настало время проверить и провести эксперимент, чтобы окончательно убедиться хотя бы на счет распределения.

Решение было простым и эффективным — собрать статистику, получить объективные данные и посмотреть на результаты.

Предмет исследования

В Unity существует несколько способов генерации случайных чисел — мы протестировали пять.

1. System.Random.Next(). Генерирует целые числа (integer) в заданном диапазоне значений.
2. System.Random.NextDouble(). Генерирует числа двойной точности (double) в диапазоне от [0; 1).
3. UnityEngine.Random.Range(). Генерирует числа одинарной точности (float) в заданном диапазоне значений.
4. UnityEngine.Random.value. Генерирует числа одинарной точности (float) в диапазоне от [0; 1).
5. Unity.Mathematics.Random.NextFloat(). Часть новой библиотеки Unity.Mathematics. Генерирует числа одинарной точности (float) в заданном диапазоне значений.

Практически везде в документации было указано равномерное распределение, за исключением UnityEngine.Random.value (где распределение не указано, но по аналогии с UnityEngine.Random.Range() также ожидалось равномерное) и Unity.Mathematics.Random.NextFloat() (где в основе лежит алгоритм xorshift, а значит, снова нужно ждать равномерное распределение).

По умолчанию за ожидаемые результаты брали те, что указаны в документации.

Методика

Мы написали небольшое приложение, которое генерировало последовательности случайных чисел каждым из представленных способов и сохраняло результаты для дальнейшей обработки.

Длина каждой последовательности — 100 000 чисел.
Диапазон значений случайных чисел — [0, 100).

Данные собирали с нескольких целевых платформ:

• Windows
  — Unity v2018.3.14f1, Editor mode, Mono, .NET Standard 2.0
• macOS
  — Unity v2018.3.14f1, Editor mode, Mono, .NET Standard 2.0
  — Unity v5.6.4p4, Editor mode, Mono, .NET Standard 2.0
• Android
  — Unity v2018.3.14f1, сборка на устройство, Mono, .NET Standard 2.0
• iOS
  — Unity v2018.3.14f1, сборка на устройство, il2cpp, .NET Standard 2.0

Реализация

У нас есть несколько разных способов генерации случайных чисел. Для каждого из них напишем отдельный класс-обертку, который должен предоставить:

1. Возможность задать диапазон значений [min/max). Будет задаваться через конструктор.
2. Метод, возвращающий СЧ. В качестве типа выберем float, как более общий.
3. Наименование способа генерации для маркировки результатов. Для удобства в качестве значения будем возвращать полное имя класса + имя метода, используемого для генерации СЧ.

Сначала объявим абстракцию, которая будет представлена интерфейсом IRandomGenerator:

namespace RandomDistribution
{
    public interface IRandomGenerator
    {
        string Name { get; }

        float Generate();
    }
}

Реализация System.Random.Next()

Этот метод позволяет задать диапазон значений, но он возвращает целые числа (integer), а нужны float. Можно просто интерпретировать integer как float, а можно расширить диапазон значений на несколько порядков, компенсируя их при каждой генерации СЧ. Получится что-то вроде fixed-point с заданной порядком точностью. Будем использовать этот вариант, так как он более близок к настоящему float значению.

using System;

namespace RandomDistribution
{
    public class SystemIntegerRandomGenerator : IRandomGenerator
    {
        private const int DefaultFactor = 100000;
        
        private readonly Random _generator = new Random();
        private readonly int _min;
        private readonly int _max;
        private readonly int _factor;


        public string Name => "System.Random.Next()";


        public SystemIntegerRandomGenerator(float min, float max, int factor = DefaultFactor)
        {
            _min = (int)min * factor;
            _max = (int)max * factor;
            _factor = factor;
        }


        public float Generate() => (float)_generator.Next(_min, _max) / _factor;
    }
}

Реализация System.Random.NextDouble()

Здесь фиксированный диапазон значений [0; 1). Чтобы спроецировать его на заданный в конструкторе используем простую арифметику: X * (max ? min) + min.

using System;

namespace RandomDistribution
{
    public class SystemDoubleRandomGenerator : IRandomGenerator
    {
        private readonly Random _generator = new Random();
        private readonly double _factor;
        private readonly float _min;


        public string Name => "System.Random.NextDouble()";


        public SystemDoubleRandomGenerator(float min, float max)
        {
            _factor = max - min;
            _min = min;
        }


        public float Generate() => (float)(_generator.NextDouble() * _factor) + _min;
    }
}

Реализация UnityEngine.Random.Range()

Этот метод статического класса UnityEngine.Random позволяет задать диапазон значений и возвращает СЧ типа float. Никаких дополнительных преобразований делать не придется.

using UnityEngine;

namespace RandomDistribution
{
    public class UnityRandomRangeGenerator : IRandomGenerator
    {
        private readonly float _min;
        private readonly float _max;


        public string Name => "UnityEngine.Random.Range()";


        public UnityRandomRangeGenerator(float min, float max)
        {
            _min = min;
            _max = max;
        }


        public float Generate() => Random.Range(_min, _max);
    }
}

Реализация UnityEngine.Random.value

Свойство value статического класса UnityEngine.Random возвращает СЧ типа float из фиксированного диапазона значений [0; 1). Спроецируем его на заданный диапазон тем же способом, что и при реализации System.Random.NextDouble().

using UnityEngine;

namespace RandomDistribution
{
    public class UnityRandomValueGenerator : IRandomGenerator
    {
        private readonly float _factor;
        private readonly float _min;


        public string Name => "UnityEngine.Random.value";


        public UnityRandomValueGenerator(float min, float max)
        {
            _factor = max - min;
            _min = min;
        }


        public float Generate() => (float)(Random.value * _factor) + _min;
    }
}

Реализация Unity.Mathematics.Random.NextFloat()

Метод NextFloat() класса Unity.Mathematics.Random возвращает СЧ типа float и позволяет задать диапазон значений. Нюанс лишь в том, что каждый экземпляр Unity.Mathematics.Random придется инициализировать некоторым seed — так мы избежим генерации повторяющихся последовательностей.

using Unity.Mathematics;

namespace RandomDistribution
{
    public class UnityMathematicsRandomValueGenerator : IRandomGenerator
    {
        private Random _generator;
        private readonly float _min;
        private readonly float _max;


        public string Name => "Unity.Mathematics.Random.NextFloat()";


        public UnityMathematicsRandomValueGenerator(float min, float max)
        {
            _min = min;
            _max = max;
            _generator = new Random();
            _generator.InitState(unchecked((uint)System.DateTime.Now.Ticks));
        }


        public float Generate() => _generator.NextFloat(_min, _max);
    }
}

Реализация MainController

Несколько реализаций IRandomGenerator готовы. Далее нужно сгенерировать последовательности и сохранить результирующий датасет для обработки. Для этого создадим в Unity сцену и небольшой скрипт MainController, который будет выполнять всю необходимую работу и попутно отвечать за взаимодействие с UI.

Зададим размер датасета и диапазон значений СЧ, а также обзаведемся методом, который возвращает массив настроенных и готовых к работе генераторов.

namespace RandomDistribution
{
    public class MainController : MonoBehaviour
    {
        private const int DefaultDatasetSize = 100000;

        public float MinValue = 0f;
        public float MaxValue = 100f;

        ...

        private IRandomGenerator[] CreateRandomGenerators()
        {
            return new IRandomGenerator[]
            {
                new SystemIntegerRandomGenerator(MinValue, MaxValue),
                new SystemDoubleRandomGenerator(MinValue, MaxValue),
                new UnityRandomRangeGenerator(MinValue, MaxValue),
                new UnityRandomValueGenerator(MinValue, MaxValue),
                new UnityMathematicsRandomValueGenerator(MinValue, MaxValue)
            };
        }

        ...
    }
}

А вот теперь формируем датасет. В данном случае генерация данных будет совмещена с записью результатов в текстовый стрим (в формате csv). Для хранения значений каждого IRandomGenerator отводится своя отдельная колонка, а первая строка содержит Name генератора.

namespace RandomDistribution
{
    public class MainController : MonoBehaviour
    {
        ...
		
        private void GenerateCsvDataSet(TextWriter writer, int dataSetSize, params IRandomGenerator[] generators)
        {
            const char separator = ',';
            int lastIdx = generators.Length - 1;

            // write header
            for (int j = 0; j <= lastIdx; j++)
            {
                writer.Write(generators[j].Name);
                if (j != lastIdx)
                    writer.Write(separator);
            }
            writer.WriteLine();

            // write data
            for (int i = 0; i <= dataSetSize; i++)
            {
                for (int j = 0; j <= lastIdx; j++)
                {
                    writer.Write(generators[j].Generate());
                    if (j != lastIdx)
                        writer.Write(separator);
                }

                if (i != dataSetSize)
                    writer.WriteLine();
            }
        }

        ...
    }
}

Осталось вызвать метод GenerateCsvDataSet и сохранить результат в файл, либо сразу передать данные по сети с конечного устройства на принимающий сервер.

namespace RandomDistribution
{
    public class MainController : MonoBehaviour
    {
        ...
		
        public void GenerateCsvDataSet(string path, int dataSetSize, params IRandomGenerator[] generators)
        {
            using (var writer = File.CreateText(path))
            {
                GenerateCsvDataSet(writer, dataSetSize, generators);
            }
        }


        public string GenerateCsvDataSet(int dataSetSize, params IRandomGenerator[] generators)
        {
            using (StringWriter writer = new StringWriter(CultureInfo.InvariantCulture))
            {
                GenerateCsvDataSet(writer, dataSetSize, generators);
                return writer.ToString();
            }
        }

        ...
    }
}

Исходники проекта лежат на GitLab.

Результаты

Чуда не произошло. Что ожидали, то и получили — во всех случаях равномерное распределение без намека на заговоры. Отдельные графики по платформам прикладывать не вижу смысла — они все показывают примерно одинаковые результаты.

Действительность такова:


Визуализация последовательностей на плоскости от всех пяти способов генерации:


И визуализация в 3D. Оставлю только результат System.Random.Next(), чтобы не плодить кучу одинакового контента.


Рассказанная во вступлении история про нормальное распределение UnityEngine.Random не повторилась: либо она изначально была ошибочной, либо что-то с тех пор изменилось в движке. Зато теперь мы уверены.