Одна из самых труднорешаемых задач в системах автоматизированного проектирования – скругления при моделировании объектов сложных форм. За построение скруглений, как и за всю геометрию в САПР, отвечает геометрическое ядро.

С точки зрения разработчика ядра охватить все варианты скруглений невозможно ввиду их бесконечного разнообразия. Наши математики постоянно добавляют в ядро C3D новые частные случаи, а недавно сделали скругление трех граней (или полное скругление).

В чем его сложность и как работает алгоритм, рассказывает Анна Ладилова, математик-программист C3D Labs.

Что такое «полное скругление»

Допустим, у нас есть тело с тремя цепочками граней – центральной (верхней) и боковыми (правой и левой). Требуется заменить центральную грань поверхностью скругления, которая бы гладко стыковалась с соседними боковыми гранями. Эта новая поверхность и будет полным скруглением. В общем случае она имеет переменный радиус, определяемый автоматически.



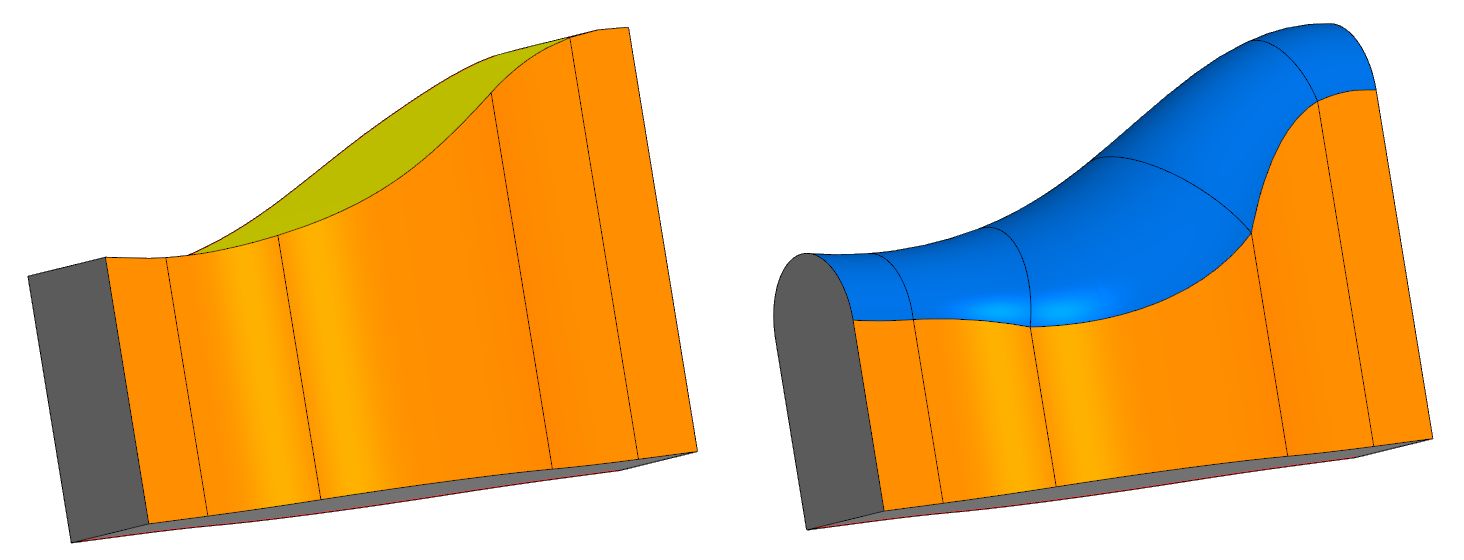
Во многих известных CAD-системах операция полного скругления (full-round fillet) реализована, но ее математика не раскрывается.


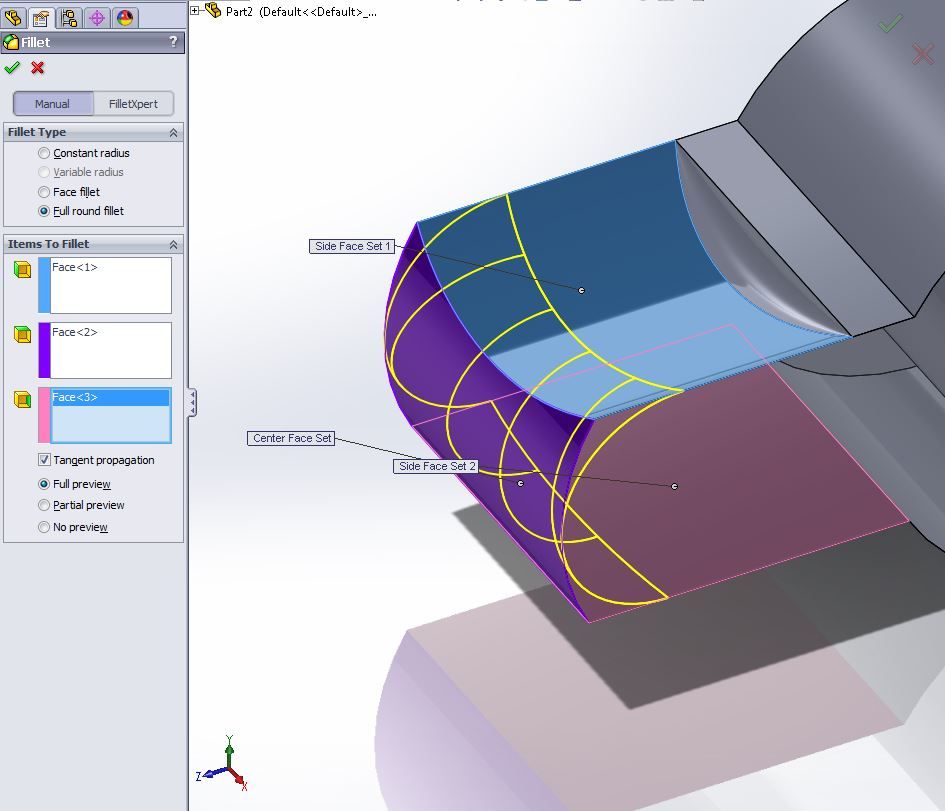
Операция Full round fillet в Solidworks

Поэтому мы разработали собственный алгоритм. И он отличается от алгоритмов других разработчиков.

Операции, хотя и называются одинаково, но приводят к немного разным результатам. Это говорит о том, что в SolidWorks скруглению трех граней дается другое определение.


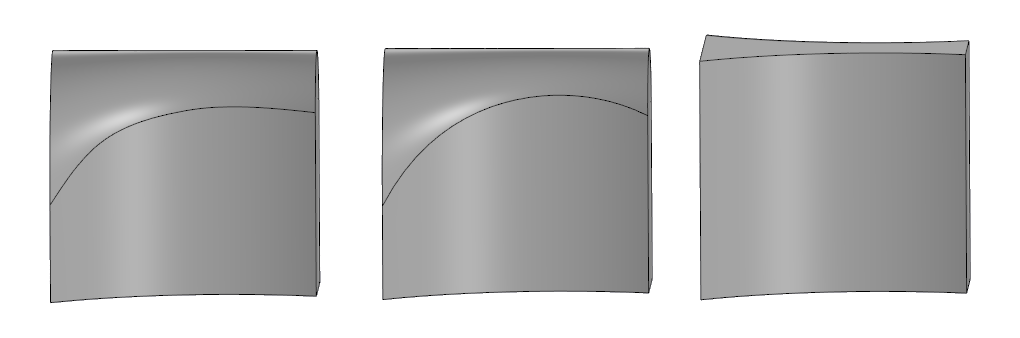
Справа — исходная модель, в центре полное скругление в SolidWorks, слева — в C3D.

Алгоритм построения полного скругления

Задача построения любого вида скруглений включает в себя несколько этапов:

1. Разбить заданную цепочку на элементарные составляющие (для скругления трех граней это ровно три грани: левая, правая и центральная).
2. Последовательно упорядочить элементарные составляющие.
3. Построить поверхность скругления для каждой элементарной составляющей.
4. «Сшить» ребрами соседние поверхности скругления.
5. Обработать торцевые участки цепочки скруглений, т. е. корректно соединить их с модифицируемым телом.

Ключевым моментом в этой процедуре является третий шаг: построить поверхность скругления для трех заданных граней.

Для построения искомой поверхности первоначально необходимо определить кривые, по которым скругление касается каждой из трех граней. В общем случае эти кривые можно построить только как сплайны, проходящие через известные точки, которые рассчитаны заранее.

Рассмотрим, как можно вычислить тройку точек – по одной на каждом сплайне.


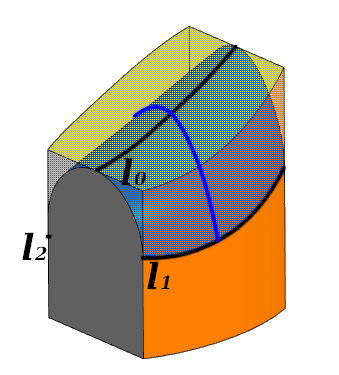
Обработка элементарной составляющей. Скругление касается каждой из трех граней по кривым l₀; l₁; l₂. Синей линией изображено поперечное сечение

В каждом поперечном сечении $$:

• $$ – рассчитывается автоматически
• $$ ортогональны касательным плоскостям поверхностей в соответствующих точках
• $$₀ – точка привязки, лежит в плоскости $$.

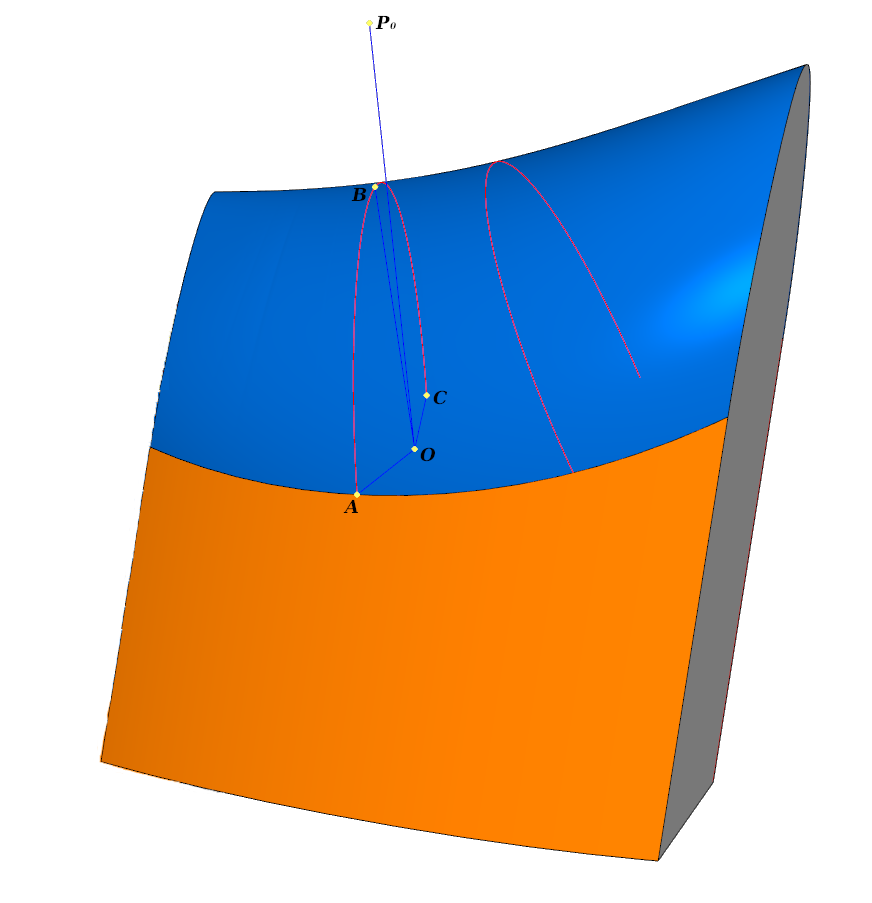
Определим исходные поверхности центральной, левой и правой граней радиус-векторами в некоторой области определения. Пусть боковые поверхности задаются радиус-векторами $$₁$$ и $$₂$$, а центральная – $$₀$$. Введем положительный числовой параметр $$.

Обозначим через $$₀$$, $$₁$$, $$₂$$ единичные нормали к соответствующим поверхностям, направленные «внутрь».


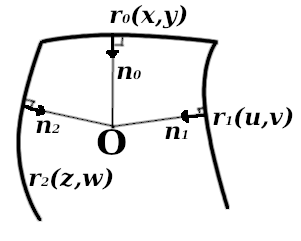
Поперечное «сечение» при построении скругления

Потребуем, чтобы концы этих нормалей, растянутых в $$ раз, попали в одну точку – точку $$.

В терминах дифференциальной геометрии наши требования можно сформулировать системой из семи уравнений с семью параметрами:

$$₀$$ = $$₁$$,
$$₀$$ = $$₂$$,
($$₀$$ — $$₀, $$₁$$ — $$₀, $$₂$$ — $$₀) = $$,

где

• $$ — переменный радиус
• $$₀ — точка привязки
• $$ — переменные из области определения параметров.

Используя алгоритмы численных методов (например, метод Ньютона), мы находим решение этой системы: $$₀, $$₀, $$₀, $$₀, $$₀, $$₀, $$₀.

Решение определяет точки касания с поверхностями:

• $$₀($$₀, $$₀),
• $$₁($$₀, $$₀),
• $$₂($$₀, $$₀),

а также радиус $$₀.

Пробегая некоторый набор точек $$₀, мы получаем наборы троек точек касания с поверхностями, по которым можно восстановить «кривые касания» $$₀, $$₁, $$₂ как сплайны Эрмита, проходящие через рассчитанные точки.

Область определения [$$_min, $$_max] у всех кривых одна и та же, причем параметру $$_i соответствуют точки $$_0i, $$_1i, $$_2i. Далее по этим кривым производится расчет нужного сечения скругления.

Зафиксируем некоторый параметр $$ и вычислим для него точки:

• $$₀$$
• $$₁$$
• $$₂$$.

Построим сплайновую кривую, проходящую через эти точки и ортогональную в них векторам нормали $$₀$$, $$₁$$, $$₂$$ соответственно.

Если слегка изменить постановку задачи и искать кривую по заданным точкам и касательным векторам в этих точках, то методы, которыми можно реализовать такой сплайн, можно найти, например, в книге Николая Голованова «Геометрическое моделирование».

В книге подробно описаны методы скругления ребра тела, в частности, показано, что поперечное сечение скругления может быть реализовано как NURBS-кривая, определенная тремя точками. В случае скругления трех граней аналогичная кривая будет определяться пятью точками.

Итак, для каждого параметра $$ мы можем определить набор точек для построения NURBS, а следовательно, определить каждую точку поперечного сечения поверхности скругления. Таким образом, задача построения поверхности полностью решена.

В описании этой части алгоритма остался небольшой вопрос — как «правильно» выбрать набор точек $$₀, соответствующих поперечному сечению, по которым можно будет легко восстановить «кривые касания» $$₀, $$₁, $$₂?

Представляется разумным брать их с некоторой заранее выбранной кривой. В детали построения этой кривой мы вдаваться не будем, отметим только, что она должна быть гладкой, без самопересечений и «усреднять» цепочки ребер, ограничивающих слева и справа центральную грань.


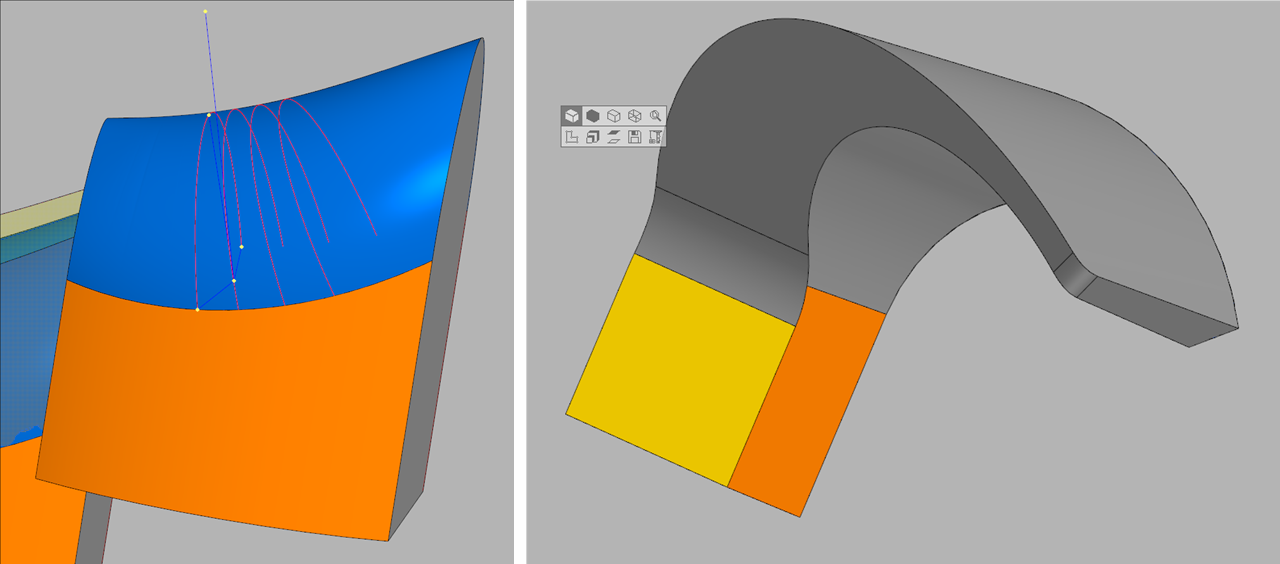
Слева поперечные сечения, зависящие от точки $$₀.
Справа фигуры могут быть достаточно сложными, поэтому правильно выбрать «вспомогательную» кривую — это отдельная задача.

Теперь, когда мы умеем строить поверхности скругления для простейших элементарных случаев, можно перейти к более сложной задаче: построить поверхность для цепочки граней.
Здесь основная проблема — «сшить» соседние поверхности гладким образом. Это четвертый шаг алгоритма.

Трудность заключается именно в гладкости сшивки, поскольку поверхности построены при разных начальных данных. Чтобы обеспечить гладкость, приходится прибегать к различным ухищрениям: менять направление и длину векторов производных в продольном направлении на некотором расстоянии от границы, менять значения производных весовых функций на границах и т.д. Результаты видны на рисунке: более гладкие линии «зебры» соответствуют более гладкой поверхности.




Вверху модель без алгоритма сглаживания. Внизу — после применения алгоритма.

Итог

В результате наших изысканий геометрическое ядро C3D умеет строить поперечное сечение скругления, опорные кривые, скругление трех граней; умеет сглаживать поверхность за счет выбора параметризации; частично умеет гладко стыковать соседние поверхности скругления.


Автор — Анна Ладилова, к.ф.-м.н., математик-программист C3D Labs