Перевод: Привет, Хабр! Представляю вашему вниманию перевод статьи "A Quick Intro to Recursion in Javascript" Yazeed Bzadough.

Примечание. Рекурсия не единожды обсуждалась на хабре, но данная статья даёт базовое понимание рекурсии. Это будет полезно начинающим разработчикам. Также, данная статья является моим первым переводом, поэтому прошу оставлять свои комментарии с конструктивной критикой по переводу и статье.

Функция продолжает вызывать себя пока не будет остановлена.

Начинающие разработчики часто плохо понимают рекурсию. Возможно, это вызвано тем, что в обучающих материалах часто используются алгоритмические примеры (числа Фибоначчи, связные списки).

В данной статье мы будем использовать всего один простой пример.

Основная идея

Рекурсией называется функция, которая вызывает сама себя пока не будет остановлена. Если она не будет остановлена, то продолжит вызывать себя бесконечно.

Рекурсивные функции позволяют выполнить одно и тоже действие несколько раз. Это как раз то, для чего используются циклы for и while. Иногда рекурсия является более элегантным решением задачи.

Функция обратного отсчёта

Давайте создадим функцию обратного отсчёта, которая будет вести отсчёт от заданного числа.
Использовать данную функцию мы будем следующим образом:

countDownFrom(5);
// 5
// 4
// 3
// 2
// 1

Алгоритм решения задачи можно описать так:

1. Получаем параметр number. Это наша отправная точка.
2. Идём от значения параметра number до 0, логируя результат.

Сначала рассмотрим решение с помощью цикла, а затем рекурсивное решение.

Императивный подход (циклы)

function countDownFrom(number) {
    for (let i = number; i > 0; i--) {
        console.log(i);
    }   
}

countDownFrom(5);
// 5
// 4
// 3
// 2
// 1

Это решение содержит оба шага алгоритма, описанного выше.

1. Получаем параметр number. Это наша отправная точка.
2. Идём от значения параметра number до 0, логгируя результат.

Рекурсивный подход

function countDownFrom(number) {
    if (number === 0) {
        return;
    }

    console.log(number);    
    countDownFrom(number - 1);
}

countDownFrom(5);
// 5
// 4
// 3
// 2
// 1

Это решение также содержит все шаги:

This one also passes.

1. Получаем параметр number. Это наша отправная точка.
2. Идём от значения параметра number до 0, логгируя результат.

Оба варианта приводят к одному результату, но разными путями.

Отладка императивного решения

Для большей наглядности добавим debugger в наше императивное решение и проследим за выполнением, используя Chrome Developer Tools.

function countDownFrom(number) {
    for (let i = number; i > 0; i--) {
        console.log(i);
        debugger;
    }   
}

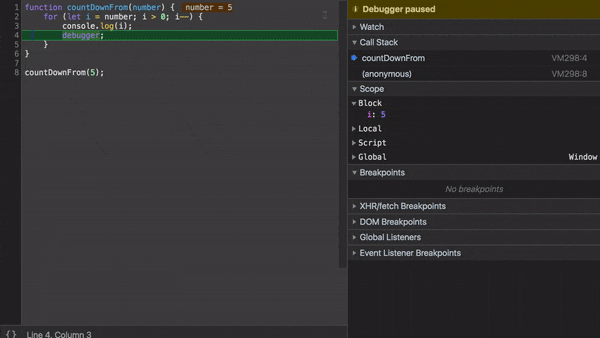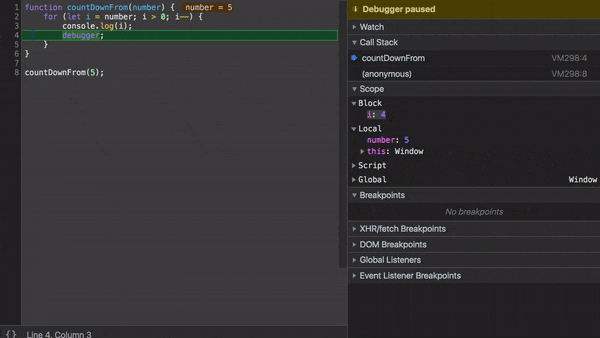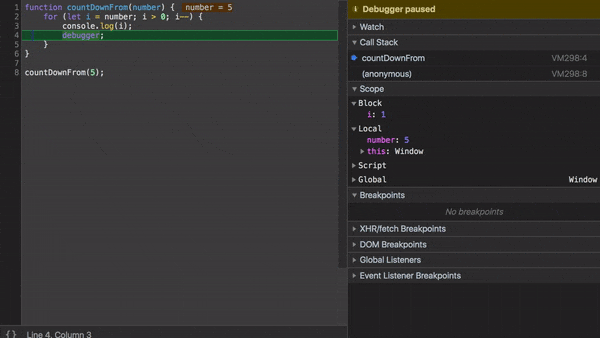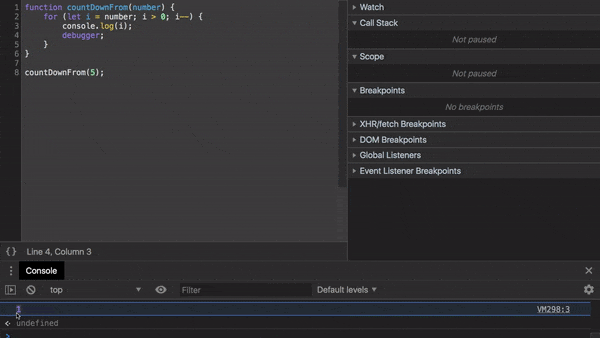
Видите как дополнительная переменная i используется для отслеживания текущего значения number?

Вы уменьшаете значение i, а когда она достигает значения 0, выполнение прекращается.

Отладка рекурсивного решения

function countDownFrom(number) {
    if (number === 0) {
        return;
    }

    console.log(number);

    debugger;

    countDownFrom(number - 1);
}

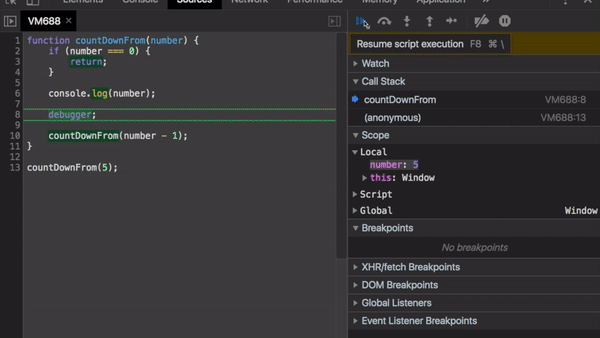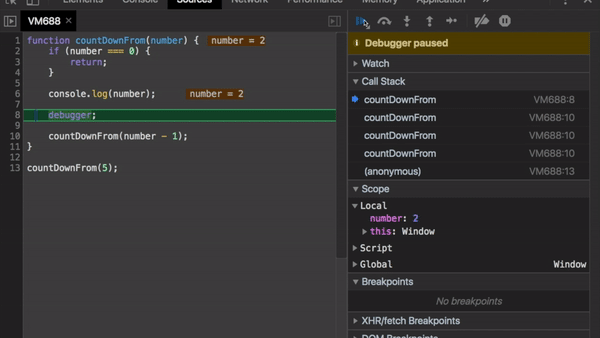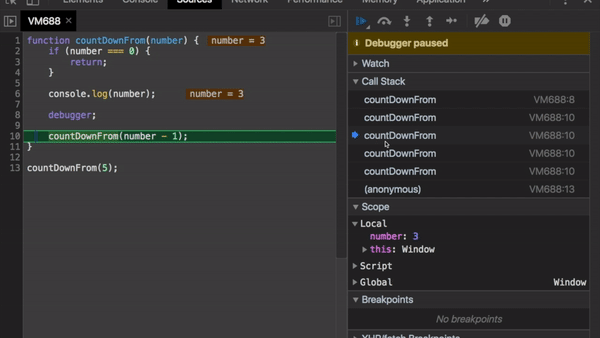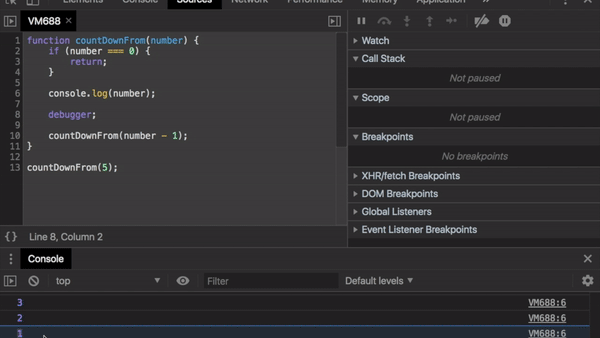
Рекурсивной версии не нужна дополнительная переменная для отслеживания прогресса выполнения. Обратили внимание на то, как растёт стек вызовов?

Это вызвано тем, что каждый вызов countDownFrom добавляется в стек со значением number - 1.

Так мы каждый раз передаём обновленное значение number. И нам не нужны дополнительные переменные!

Это основное отличие между двумя версиями.

Итеративное решение использует внутреннее состояние (дополнительные переменные для отсчёта и т. д.), а рекурсивное решение просто создает новый вызов с обновленным параметром.

Но как обе версии узнают когда необходимо остановиться?

Бесконечные циклы

Возможно, вы уже знаете о ужасных бесконечных циклах:

 THIS RUNS FOREVER, BE WARNED 
while (true) { console.log('WHY DID YOU RUN THIS?!' }

 THIS RUNS FOREVER, BE WARNED 
for (i = 0;;) { console.log('WHY DID YOU RUN THIS?!') }

В теории, они будут выполняться бесконечно, но, скорее всего, программа и браузер завершат свою работу.

Примечание переводчика: завершение работы будет связано с достижением максимального размера стека вызовов. Максимальный размер стека вызовов зависит от конкретного браузера и может сильно варьироваться. Перейдя по ссылке Вы можете оценить предел рекурсивных вызовов функции в вашем браузере и сравнить его с результатами других пользователей

Вы можете предотвратить это добавив условие выхода из цикла.

 This does not run forever
x = 0;
while (x < 3) { console.log(x); x++; }

 This does not run forever
for (x = 0; x < 3; x++) { console.log(x); }

В обоих случаях мы логируем значение x, инкрементируем x, и останавливаем выполнение когда значение x становится равно 3. Наша функция countDownFrom использует схожую логику:
Our countDownFrom function had similar logic.

// Stop at 0
for (let i = number; i > 0; i--)

Повторим. Циклам необходима дополнительная переменная, чтобы они могли остановиться.

Бесконечная рекурсия

Рекурсия также представляет опасность. Очень легко написать рекурсивную функцию, которая приведёт к завершению работы браузера.

THIS RUNS FOREVER, BE WARNED
function run() {
    console.log('running');
    run();
}

run();
// running
// running
// ...

Без условия остановки, функция run будет бесконечно вызывать сама себя. Вы можете исправить это с помощью условия(if):

 You can fix that with an if statement.

 This does not run forever

function run(x) {
    if (x === 3) return;

    console.log('running');
    run(x + 1);
}

run(0);
// running
// running
// running

// x is 3 now, we're done.

Базовое условие

Наша рекурсивная функция countDownFrom имеет одно базовое условие

if (number === 0) {
    return;
}

Здесь та же идея, что и в цикле. Всегда нужно помнить, что необходимо базовое условие.

Выводы

• Рекурсией называется процесс когда функция вызывает сама себя пока не будет остановлена
• Рекурсию можно использовать вместо циклов
• Если не остановить рекурсию, она приведёт к "падению" вашей программы
• Базовое условие останавливает рекурсию. Не забывайте о нём!
• Циклы используют переменные состояния для отслеживания и отсчёта. В рекурсии используются только переданные параметры.
  

Примечание переводчика: в оригинальной статье нет упоминания хвостовой рекурсии. Хвостовая рекурсия представляет из себя частный случай рекурсии и заключается в том, что рекурсивный вызов является последней оперецией перед выходом из функции. Стоит отметить, что решение, использующее хвостовую рекурсию, всегда может быть преобразовано в итерационное решение.