Как-то раз я случайно увидел, как мой коллега решает джуниорскую задачку разворачивания двусвязного списка на C++. И в тот момент странным мне показалось не то, что он лид и давно перерос подобное, а само решение.
Вернее, не так.
Решение было стандартным: тот же линейный проход с заменой указателей в каждом узле, как и писали сотни тысяч людей до него. Ничего необычного или сложного, но при взгляде на него у меня возникло два вопроса:
- Почему по умолчанию все решают задачу именно так?
- Можно ли сделать лучше?
Вкратце о матчасти. Если вы знаете, что такое двусвязный список, следующий абзац можно пропустить.
Двусвязный список ― одна из базовых структур данных, знакомство с ней обычно происходит на ранних этапах обучения программированию. Это коллекция, состоящая из последовательности узлов, которые содержат некие данные и попарно связаны друг с другом ― то есть, если узел A ссылается на B как на следующий, то узел B ссылается на A как на предыдущий. На практике вы можете встретить эту структуру в таких контейнерах, как std::list в C++, LinkedList в C# и Java. Скорее всего, вы найдёте её реализацию в стандартной библиотеке любого другого языка.
Далее в тексте будут описаны основные свойства и операции над таким списком с указанием вычислительной сложности.
Теперь вернёмся к озвученным ранее вопросам.
Я заглянул в условие задачи и увидел ответ на первый. Вот он:
struct node
{
int data;
node* next;
node* prev;
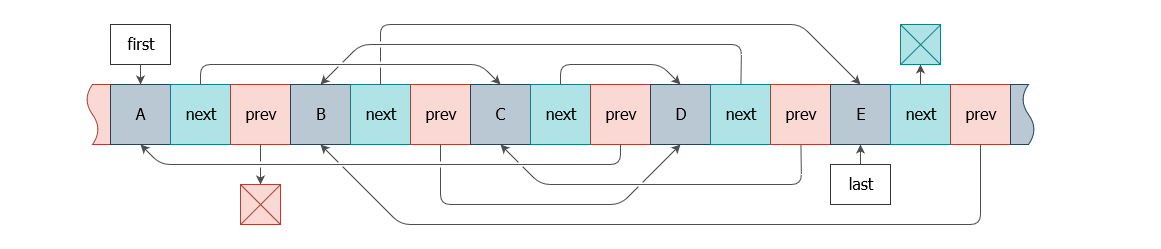
};Эта структура уже была в самом условии. Не видите проблемы? Тогда посмотрите на схему:

Объясню. Код структуры узла выше ― некий канон, который повторяет схему на изображении. Мало кто сомневается, что эта структура должна существовать и выглядеть именно так в любой реализации этого списка, с поправкой на синтаксис языка и кодстайл.
Попробуйте в таких условиях получить список EBDCA. Линейный разворот всего списка тут ― решение очевидное и логичное, других вариантов нет. На первый взгляд.
Несколько минут я думал над ответом на вопрос, так ли это, и во время рабочего перерыва вбросил, что смогу выдать решение, у которого будет разворот за O(1), а результатом всё ещё останется двусвязный список. Спорили всей командой за обедом, мне никто не поверил. К тому времени я уже всё придумал, нужно было только расписать.
Вместо схемы и навязанного лейаута узла я решил отталкиваться от самих свойств структуры данных. Всё, что вы ожидаете от двусвязного списка, можно описать так:
- Список состоит из узлов, с каждым из которых связаны данные.
- Каждый узел связан с предыдущим узлом. Если такой связи нет, то это начальный узел списка.
- Каждый узел связан со следующим узлом. Если такой связи нет, то это конечный узел списка.
- Можно получить начальный и конечный узлы списка за константное время.
- Можно вставить и удалить узлы (из/в середину/начало/конец) за константное время.
- За константное же время можно получить следующий/предыдущей узел для исходного или убедиться, что такого нет и мы у границы коллекции.
- Как следствие предыдущего пункта – можно обойти список в любую сторону. За линейное время, разумеется.
Ключевой элемент здесь ― связи. А связь ― это не всегда указатель/ссылка в прямом смысле. Реализация должна позволять получать связанные данные и информацию о соседях узла, и совсем не обязательно в виде полей какого-то экземпляра. Более того, каноничный лейаут может даже вредить производительности. Например, во время прямого прохода по списку в классической реализации процессору на каждом шаге приходится подгружать в кэш-линии все поля узла, и существует совсем небольшая вероятность того, что соседние узлы окажутся в одной линии, даже если вы используете какой-то особый аллокатор.
«Что? Какие кэш-линии?» ― спросите вы: «Я кликнул почитать про разворот списка!»
Краткое отступление, чтобы вы не потеряли нить к этому моменту, узнав о такой заботе по отношению к каким-то там кэш-линиям с моей стороны. Я занимаюсь разработкой игр, поэтому у меня профдеформация: я пытаюсь оптимизировать всё, что плохо лежит. В последнее время я стараюсь следовать принципам Data-Oriented Design: это не название секты, а набор рекомендаций, помогающих машинам эффективнее справляться с задачами, которые мы перед ними ставим. На Хабре статьи по теме можно найти по тегу DOD. И соблюдение этих правил действительно даёт плоды. Это тема для отдельной статьи, или серии статей, или даже книги.
Дело в том, что в первое мгновение я даже не думал об эффективности разворота списка, когда смотрел на решение коллеги. Я думал об оптимизации всего лейаута коллекции. А константный разворот оказался интересным побочным продуктом.
Итак, можно повысить вероятность попадания соседних узлов в одну кэш-линию, упаковав их в один блок памяти. В таком случае вставлять новые узлы нужно в конец или любое другое свободное место, так как при удалении будут возникать «дырки» в блоке. Но тут есть свои проблемы:
- Любая операция вставки/удаления потенциально делает недействительным полученный ранее экземпляр узла, так как указатели на соседние узлы могут измениться.
- Даже если при обходе в кэш-линию попадут нужные узлы, рядом вы обнаружите поля с данными и поля с обратным указателем. Обратные указатели бесполезны при обходе и просто занимают ценнейшее пространство кэш-линии.
Да, часть проблем можно решить. Заменить указатели на индексы, например. Но лейаут остаётся прежним, и из-за этого всё ещё нельзя развернуть список за O(1), а это моя основная цель.
Тогда я решил пойти ещё дальше ― использовать структуру массивов (SoA) вместо массива структур (AoS), как было в предыдущем шаге. Получим представление примерно как на схеме:
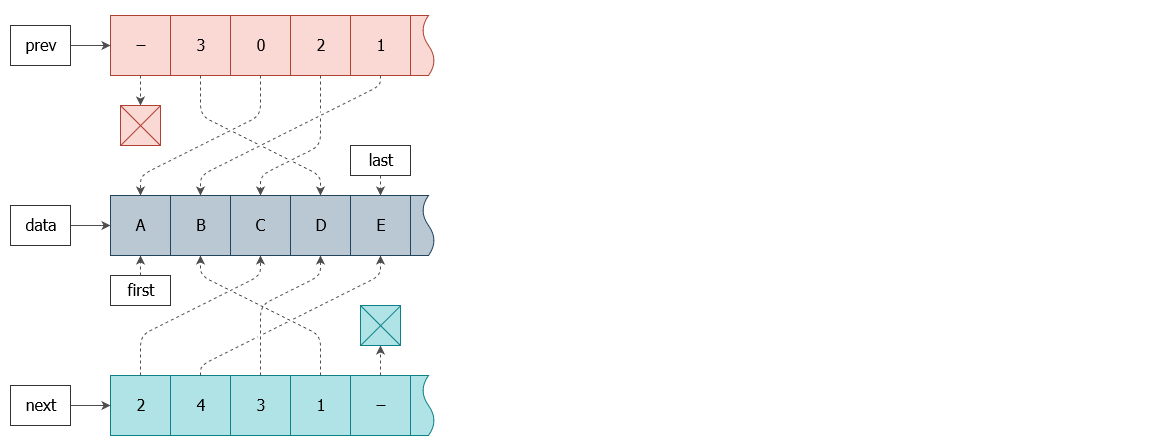
Что вам это даст? А вот что:
Узел ― это просто индекс в массиве. Его данные можно получить из data, а соседей из prev/next.
После вставки/удаления мы всё ещё имеем возможность продолжить работу с ранее полученным узлом-индексом.
Во время прохода процессор будет погружать только те данные, которые для этого прохода нужны ― то есть, prev или next в зависимости от направления. Вероятность более эффективной утилизации кэш-линии сильно повышается. А для не перемешанных участков списка она будет стопроцентной.
И знаете ещё, что?
На схеме выше изображён список ACDBE. Теперь взгляните на схему для EBDCA, в которой массив данных остаётся прежним:
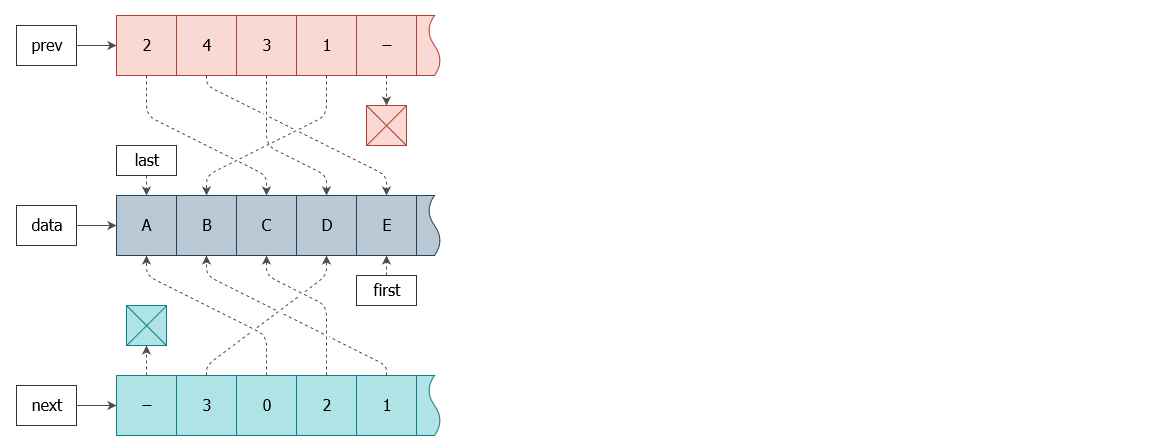
Как симметрично! Если вы думаете, что я специально подобрал такой список, чтобы всё работало, как надо, можете попробовать повторить те же операции на любой другой последовательности.
Итак, если мы будем хранить prev и next в виде указателей на блоки индексов, а first и last в виде самих индексов, что никто нам не запрещает делать, то операция разворота списка превратится в простой обмен значениями в следующих парах:
prev <-> next
last <-> first
Я не стал заморачиваться с менеджментом памяти, сделал всё на стеке. Также отсутствуют операции удаления узлов и проверки. Демонстрации работы кода это не помешает. Если кому-то будет нужно, этот кто-то может реализовать всё это под себя без особых проблем.
Итак, что в итоге получилось, без купюр и причёсывания:
template <class T, size_t Cap>
struct doubly_linked_list
{
struct node { size_t index; };
// API получения данных и соседей для узлов
T& get(node n) { return data_[n.index]; }
const T& get(node n) const { return data_[n.index]; }
node first() const { return { first_ }; }
node last() const { return { last_ }; }
node next(node n) const { return { next_[n.index] }; }
node prev(node n) const { return { prev_[n.index] }; }
bool is_valid(node n) const { return n.index < length_; }
// Алгоритмы добавления и вставки от смены лейаута сильно не пострадали
node add(T v)
{
auto index = length_;
if (length_ == 0) first_ = 0;
data_[index] = v;
next_[index] = INVALID_INDEX;
prev_[index] = last_;
next_[last_] = index;
last_ = index;
length_++;
return { index };
}
node insert_before(T v, node n)
{
auto index = length_;
data_[index] = v;
next_[index] = n.index;
auto prev = prev_[index] = prev_[n.index];
prev_[n.index] = index;
next_[prev] = index;
length_++;
if (n.index == first_) first_ = index;
return { index };
}
// …тут должны быть методы удаления, они не сильно будут отличаться от псевдокода в любом туториале,
// разве что придётся вести учёт «дырок» в отдельном массиве. Это также затронет и add/insert_before -
// там вместо length_ нужно будет забирать первую «дырку».
// Вишенка на торте – то, ради чего всё это было сделано:
void reverse()
{
std::swap(first_, last_);
std::swap(next_, prev_);
}
private:
static constexpr size_t INVALID_INDEX = SIZE_T_MAX;
T data_[Cap];
size_t indirection_[Cap * 2];
size_t *next_ = indirection_;
size_t *prev_ = indirection_ + Cap;
size_t first_ = INVALID_INDEX;
size_t last_ = INVALID_INDEX;
size_t length_ = 0;
};Тестовый запуск показал успех:
auto list = doubly_linked_list<int, 10>();
auto pos = list.add(0);
for (int i = 0; i < 5; ++i) pos = list.insert_before(i + 1, pos);
std::cout << "list";
for (auto n = list.first(); list.is_valid(n); n = list.next(n))
std::cout << list.get(n) << " ";
// > list 5 4 3 2 1 0
list.reverse();
std::cout << std::endl << "reversed";
for (auto n = list.first(); list.is_valid(n); n = list.next(n))
std::cout << list.get(n) << " ";
// > reversed 0 1 2 3 4 5На самом деле, я соврал о том, что при AoS лейауте нельзя было развернуть список так же эффективно. Можно провернуть подобный трюк и там, но уже если захотите поупражняться сами: от лишних данных в кэш-линиях это всё равно не спасёт, поэтому я не стал этим заниматься.
Для меня решение задачи с разворотом было всего лишь челленджем, так что я не планирую развивать эту реализацию в будущем. Может быть, кто-то найдёт в этом практическую пользу и сделает что-то хорошее для себя и других ― например, cache-friendly дэк или оптимальную реализацию DCEL, который можно мгновенно вывернуть наизнанку. Словом, следуйте своему воображению.
А теперь к выводам:
Для объяснения своих идей друг другу мы часто используем схемы. Это неплохо и зачастую действительно удобнее. Но иногда мы становимся заложниками такого изложения идей. В случае с двусвязным списком проблема не в схеме ― она всё ещё хороша в академическом смысле, как и классический лейаут. Проблема в том, что эту схему, как и любую другую, часто понимают буквально – как постулат, а не как одну из концепций.
В качестве второго вывода приведу базовый постулат Data-Oriented Design: знайте свои данные и то, что вы собираетесь с ними делать. Это действительно помогает повысить эффективность ваших решений. Пример с двусвязным списком и его разворотом – это всего лишь игрушка, зарядка для ума. Попробуйте взглянуть на свои решения с подобной точки зрения и обнаружите очень много интересных ходов, о которых раньше даже и не думали.
Вот и всё. И поменьше вам кэш-миссов в новом году.
Комментарии (124)

Deosis
16.12.2019 12:04+38Приведенный код — это не связный список, хотя бы потому, что сверх лимита узлы в него не добавляются.
Если уж делать разворот за константное время, то в самом списке надо дополнительно хранить куда на самом деле ссылаются указатели в узле (в прямом или инверсном порядке). но от этого пострадает скорость других операций со списком.
nshalimov Автор
16.12.2019 12:23-8Приведённый код – это всго лишь proof of concept, а не полноценная реализация. Я упомянул это в тексте. Можно убрать этот лимит и увеличивать капасити массивов при переполнении. И да, в некоторых случаях это может повлиять на время добавления нового узла. Иногда нет. Всё опять же зависит от ваших данных, и от задачи. Иногда вы просто знаете капасити наперёд.

mamont80
16.12.2019 12:52+31Только опять же. Получится не двусвязный список, а нечто вроде обычного массива. У двусвязного списка есть ряд важных свойств, из-за которых его используют, которые вы нарушили.
Например, легкое вставка кортежей одного списка в другой за O(1), добавление/удаление кортежа за O(1), и т.п.
Но идея хорошая. Не всегда требуется использовать абстракции в чистом виде.
nshalimov Автор
16.12.2019 13:12-14Вы правы, при вставке кортежа тут будет O(размер кортежа). Но для подобной задачи я бы что-нибудь иное придумал. Первое, что приходит в голову – делить эти массивы между списками, с которыми так придётся поступить (смержить).
Опять же, всё зависит от задачи, не всегда есть возможность написать эффективное общее решение.
trapwalker
17.12.2019 10:00+2И в сухом остатке ваш двусвязный список — это уже не классический двусвязный список ввиду наложения ряда ограничений на его использование и снятия ряда преимуществ.

pvl_1
16.12.2019 13:16-3Невыполнение этих требований верно только в случае, если элементы этих списков лежат в разных пулах. А если для всех списков данного типа использовать один пул (то есть три: пул данных, пул prev и пул next)? Тогда пострадает утилизация кэша, но вставки и удаления других списков в данном станут за O(1).

vassabi
08.05.2020 16:15еще можно менять функции (Если лениво сделать обертки над структурой в памяти, то как минимум лямбды нынче работают даже для компилирующихся языков) — и тогда просадка будет минимальной.

Biblusha
16.12.2019 12:19+23В этой реализациия метод add сможет добавлять элементы только до CAP.
При удалении элемента, нужно будет сдвигать массив или оставлять «мёртвые ячейки» (которые кстати потом можно заполнять, но опять их нужно будет искать).
Имхо, это не двусвязанный список, а обёртка над массивом.
netricks
16.12.2019 12:26+5Несовсем.
При удалении элемента целесообразно свопать его с последним элементом массива (и пересчетом next/prev индексов соседних элементов списка). Тогда операция будет О(1). В реализации автора это вполне возможно.
force
16.12.2019 17:19Спасибо за идею. Мне для других целей надо было, но идея интересная (я больше думал про связный список из дырок, раз уж у нас массив фиксированный и так), но тут в некоторых случаях будет эффективнее.

tangro
16.12.2019 12:30+112Что это вообще за дичь такая — «разворот двусвязного списка»? Какой смысл разворачивать двусвязные списки? По ним и так можно ходить в любом направлении — что от начала в конец, что из конца в начало. Это свойство двусвязного списка. Если на собеседовании просят двусвязный список «развернуть», то просто объясняешь, что ничего в данных менять не нужно, а нужно просто правильно воспользоваться (ну или реализовать, если их нет) реверсные итераторы типа std::rbegin и std::rend. И всё. Никаких тут нет даже О(1).

nshalimov Автор
16.12.2019 12:36+3И меня это тоже смутило, я и сам не понимаю. Сама постановка задачи. Но я её встречал множество раз со времён университета. Меня смутило само решение, которое все пишут одинаково.
Ну и ещё, кстати, в стандарте есть такой метод: en.cppreference.com/w/cpp/container/list/reverse и он работает за O(N)
wataru
17.12.2019 00:20Поддержу других комментаторов. Разворот двусвязного списка — бесполезная вещь. На интервью когда-то был смысл спрашивать про односвязные списки (когда это стало баяном — смысл пропал).
Я на многих сайтах встречал задачу именно про односвязный список. Двусвязных же не видел ни разу.

stan_volodarsky
17.12.2019 00:40А если один надо развернуть а затем конкатенировать с другим? Конкатенация классических списков делается за O(1). Разворот за O(1) очень бы помог. К сожалению, предложенная структура делает конкатенацию медленной.
Задача: придумать двусвязный список с разворотом и конкатенацией за O(1).
wataru
17.12.2019 01:08А если один надо развернуть а затем конкатенировать с другим.
Очень специфичная задача.
Не понимаю, правда, откуда такие ограничения. Ведь по списку, в конце-концов, придется пройтись — иначе зачем нам данные, которые мы никогда не трогаем. А значит, можно разворачивать все что вам надо за линию — все-равно в конце пройдемся по элементам за линию.Но соглашусь — я выразился слишком категорично. Я не имел ввиду что такой задачи вообще не может быть. Хотел лишь сказать, что разворот двусвязного списка на интервью нигде, по идее, не спрашивают. Если только интервьювер не перепутал задачу (слышал где-то про разворот списка и спросил про тот список, который знал).
Есть другая задача, где нужно быстро разворачивать часть элементов в "списке".
Вот только быстрый разворот может быть нужен в виде "разверни элементы с 10-ого по 15-ый". Тут уже нужно неявное сбалансированное дерево и будет все за логарифм, а не O(1). Такая задача может быть на олимпиаде, но никак не на интервью. Разворот же под-списка, опять же, можно делать за линию, ведь элементы в этом самом списке придется сначала найти — а это уже линейный проход.
stan_volodarsky
17.12.2019 01:17А я и имел ввиду задачу как задачу. Это может быть полезно, может быть нет. Иногда такие вещи стреляют, как фибоначчиевы кучи, например.

wataru
17.12.2019 11:46+1Кстати, решение автора эту задачу не решает. "Прямой" и "развернутый" списки нельзя хранить в одном пуле, а значит их не сканкатенировать. Нужно будет делать ссылки на внешние списки и городить условные операторы. В этом случае проще в каждом элементе держать флаг "поменяй направление движения" или тупо смотреть на обе ссылки и помнить предыдущий элемент при обходе.

Arqwer
17.12.2019 12:01Мне кажется я помню такую задачу в каком-то контесте. Там это оправдывалось тем, что операции ведутся над цепочками ДНК, и ДНК как раз часто разворачивается и конкатенируется. О биологической правдоподобности судить не могу. Задача кажется была такой: даётся N =100 000 пар чисел (i; j), и начальная последовательность. Каждую пару надо обработать так: развернуть подпоследовательность от i до j. И длинна последовательности кажется около M = 1 000 000. Если развороты делать за линейное время, то общее время получится о(NM), что не годится. Правильное решение не помню, но кажется задача не очень сложная. И про величину N и M я возможно ошибся на пару порядков.

wataru
17.12.2019 12:31Эта задача не решается списком. Потому что найти i-ую позицию в списке можно только за линию.
Тут, как я и описывал надо делать балансированное бинарное дерево по неявному ключу. Пилить его на три части в позициях i и j, потом разворачивать среднее дерево за константу через отложенный разворот (типа как делается отложенное добавление в дерево отрезков, только разворот), затем сливать 3 дерева назад. Решение будет за O((M+N) log N). Очень просто делается с помощью Treap — там есть реализация через Split и Merge.

khim
17.12.2019 03:06+2Задача: придумать двусвязный список с разворотом и конкатенацией за O(1).
Всё упрётся в определения. Возьмите обычный XOR-связный список. Его и развернуть за O(1) можно и сконкатенировать… Но является ли он двусвязным списком? Вот в чём вопрос…
Можно спорить до посинения…
stan_volodarsky
17.12.2019 09:54Не надо спорить. Надо определить что такое двусвязный список. Например:
доступ к первому и последнему элементам (O(1));
переход к следующему/предыдущему элементу (O(1));
вставка в любое место (O(1));
удаление из любого места (O(1)).
Дальше по желанию:
конкатенация (O(1));
разрезание (O(1));
разворот (O(1));
условия на сохранение указателей при модификации списка.
Разные комплекты условий будут порождать разные задачи. XOR список (почти) подходит по всем пунктам.
khim
17.12.2019 13:40Обычно считается, что «двусвязный список» — это «список с двумя связями» (банально, да?). То есть это не про «O большое», а про особенности реализации.
И вот тут уже начнётся спор — можно ли считать одно поле в элементе XOR-связаного списка двумя связями или нет.
А главное спор абсолютно бессмысленный: люди, способные в этом споре участвовать уже точно все ньюансы понимают и речь идёт только об «интеллектуальной мастурбации» — можно ли что-то назвать словом ____ или нет.
Практического выхлопа нуль…

force
16.12.2019 17:20+6Думаю, есть человеческая задача: «развернуть односвязный список», но т.к. в реальности двусвязные обычно удобнее и реализованы в языках, задача сформировалась в такого Франкенштейна.

AVI-crak
16.12.2019 17:52-4Простая файловая система — односвязный список. Реальность иногда заставляет его разворачивать в обратном направлении, это и есть человеческая задача.
А для собеседований нужно предлагать развернуть двусвязный кольцевой список. Особо одарённых нужно отстреливать на низком старте.

Static_electro
16.12.2019 12:30+25Если список двусвязный — то его можно не разворачивать. Достаточно хранить оба "конца" :)

pdima
16.12.2019 12:40+8медленное но тривиальное решение — добавить bool/enum direction_ в контейнер/итераторы;

risentveber
16.12.2019 12:47+2Ага порядок в данном случае — это лишь одно из двух направлений обхода, вообще ничего менять не нужно — просто direct_iterator и reverse_iterator сделать.

unC0Rr
16.12.2019 23:22Потеряется возможность обмениваться цепочками элементов с другими списками за О(1), если направления не совпадают.

AEP
16.12.2019 12:42+36Разговоры о кеш-линиях и массивах prev и next не нужны. Хотя бы потому, что с массивами prev и next, как уже было отмечено выше, структура не имеет права называться двусвязным списком.
Есть более «чистое» решение. Вместо указателей prev и next хранить в каждом элементе списка указатели link1 и link2. Глобально на весь список (т.е. вместе с указателями end1 и end2 на голову и хвост) хранить один битовый флаг, который отвечает за интерпретацию, какой из указателей link1 и link2 играет роль prev, а какой — next. Он же определяет, какой из двух концов считать головой, а какой — хвостом. Тогда переворот будет состоять в перевороте этого флага.
Ну или как уже заметили, если у вас C++, то итераторы std::rbegin и std::rend уже делают что-то подобное.
Ну и стандартная задача на интервью — это все-таки разворот односвязного, а не двусвязного списка.
nshalimov Автор
16.12.2019 13:00-9Как вы быстро и безапелляционно отмели разговоры о кеш-линиях и не дали права называться этому двусвязным списком.
Если это снаружи выглядит для пользователя как список, ведёт себя как список – то это список.
Да, вариант с флажком тоже имеет право на существование, кто-то мне его предлагал, но это показалось мне слишком простым. Плюс интепрпретация указателей в зависимости от состояния этого флажка – ещё один уровень перенаправления (level of indirection). В виде бранча (return is_reversed? link1: link2) или в виде взятия по индексу (return links[is_reversed]). Не сказал бы, что это решение будет «чище».
Кто-то даже предлагал редактировать виртуальную таблицу (!) ноды, но это уж совсем экзотика
playermet
16.12.2019 14:26+17Если это снаружи выглядит для пользователя как список, ведёт себя как список – то это список.
Неа. То что может как-то выглядеть снаружи, являясь чем угодно внутри — это абстрактный тип данных, который описывает внешнее поведение. Например, стек, очередь или ассоциативный массив. Но список — не абстрактный тип данных, это структура данных, и описывает она как ни странно структуру данных в памяти и операции над ней. Такое деление нужно потому что АТД выбирают по интерфейсу (FIFO/LIFO/etc.), а структуры данных по внутренним свойствам (сложности операций по времени и памяти).
А так-то немного магии и обертка позволит хоть стандартной библиотечной хеш-таблице снаружи выглядеть как список, но это совершенно определенно не будет список. Ну или например префиксное дерево которое снаружи выглядит как хеш-таблица точно не является хеш-таблицей.
alex_zzzz
16.12.2019 15:14+1Но список — не абстрактный тип данных
Просто "список" — вполне себе абстрактный. Двусвязный — другое дело.

playermet
16.12.2019 18:17+3Такой АТД как список действительно есть. Но связный список (одно или двух) — это именно структура данных. Под «списком» в комментарии выше я подразумевал связный список. И задача разворота тоже подразумевает именно его.

vitaliy2
17.12.2019 10:03Мне всегда казалось, что двусвязный список описывает структуру так:
Храним:
— Для каждого элемента: Значение
— Для каждого элемента: Ссылку на предыдущий элемент
— Для каждого элемента: Ссылку на следующий элемент
— Общую ссылку на первый элемент
— Общую ссылку на последний элемент
— Как результат, возможно добавление/удаление за O(1), обход за O(n)
(по крайней мере если менеджер памяти позволяет добавлять и удалять элементы за O(1), а также позволяет за O(1) получить значение по ссылке на него).
Список из статьи удовлетворяет этим условиям. Но из-за особенностей используемого менеджера памяти (выделение памяти на массиве поверх стандартных менеджеров ОС и программы) добавление делается за амортизированное O(1), а не гарантированное O(1), что в принципе в большинстве случаев норм. Т. е. если придираться, то только по поводу амортизации.
playermet
17.12.2019 23:12Конкретно та структура данных, что сейчас представлена в статье не может расширяться после исчерпания вместимости. Чтобы дойти до обсуждения амортизированной сложности нужно сначало модифицировать ее чтобы она обходила это ограничение, а уже потом смотреть как именно она это делает. Плюс нужно как-то обрабатывать удаление элементов и операции над двумя списками (объединение как минимум). Но вообще я не столько оспаривал принадлежность представленной структуры к семейству списков, сколько конкретное процитированное утверждение.

vitaliy2
18.12.2019 12:05нужно обрабатывать удаление
Это легко делается за O(1). Элемент удаляется, а на его место ставится просто последний.Чтобы дойти до обсуждения амортизированной сложности
Вообще да, если так подумать, можно сделать вставку даже за гарантированное O(1), а не амортизированное. Тогда это точно будет связный список (но опять же, за счёт того, что теперь выделение памяти будет за гарантированное O(1), т. е. возвращаемся к менеджеру памяти).объединение
Я не уверен, что всякий связный список поддерживает эту операцию. Но если что, сделать её несложно.
playermet
18.12.2019 18:36Элемент удаляется, а на его место ставится просто последний.
И тут итератор ломается, и его нужно чинить. В любом случае интерфейс в этом месте уже не будет совпадать с двусвязным списком.можно сделать вставку даже за гарантированное O(1)
И при этом все другие свойства останутся такими же? Как минимум разворот для которой эта структура и затевалась перестанет быть O(1). А еще очень интересно насколько «легким» станет реализация удаления элементов после такой модификации.Я не уверен, что всякий связный список поддерживает эту операцию.
Во всякий код двусвязного списка ее можно добавить, и получить O(1) хоть за вставку списка в середину списка, если средний узел заранее известен.Но если что, сделать её несложно.
Только сложность будет не как у двусвязных списков.
То что получится в итоге с вашего описания скорее всего будет Unrolled Linked List с Structure Peeling.
vitaliy2
19.12.2019 01:29И тут итератор ломается, и его нужно чинить.
Почему это ломается? Всё норм.интерфейс уже не будет совпадать
А причём тут интерфейс? Интерфейсов можно придумать много каких. К структуре данных это отношения иметь не будет.И при этом все другие свойства останутся такими же?
Вроде, да. Просто когда память кончилась, выделяем новый кусок, а куски складируем в массив. Чтобы обратиться к нужному куску, например, делаем битовый сдвиг, а к элементу в куске — битовое И. На удаление это не влияет, сама реализация не должна сильно поменяться.можно добавить
Можно много чего добавить в разные реализации. Связный список тут не при чём.
Но реализация автора всё-равно позволяет добавлять элементы в середину, почему бы и нет… Соединение списков тоже, наверное, можно сделать. А если все списки хранить на одном массиве, то тем более (просто хранение в одном массиве менее эффективно).Только сложность будет не как у двусвязных списков.
Почему? Думаю, Вы не так поняли алгоритм автора. Все операции за O(1). Просто вместо выделения памяти с помощью стандартного менеджера память выделяется на массиве. Поэтому, наверное, Вы и строите претензии, что полагаете о каком-то другом списке, не который опубликовал автор.
khim
19.12.2019 04:50+1Почему это ломается? Всё норм.
Это как это «всё норм»? Итератор, указывавший ранее на тот элемент, который, случайно, оказался в конце массива — таки сломается. А в двусвязном списке такого быть не должно.Интерфейсов можно придумать много каких. К структуре данных это отношения иметь не будет.
Погодите: если вы не фиксируете ни интерфейс, ни реализацию, то как вы вообще отличаете односвязный список от двусвязного или их оба — от фибоначчевой кучи?Поэтому, наверное, Вы и строите претензии, что полагаете о каком-то другом списке, не который опубликовал автор.
То, что опубликовал автор — это не двусвязный список, извините. Структура достаточно интересная — но не двусвязный список ни разу…
vitaliy2
19.12.2019 11:19таки сломается
Если правильно реализовать, ничего не ломается.
Например, можно хранить номер элемента по ссылке. При физическом перемещении элементов менять этот номер. Все остальные куски кода будут получать уже новый номер мгновенно.
Это только самый простой пример, можно сделать и лучше.Погодите: если вы не фиксируете ни интерфейс, ни реализацию, то как вы вообще отличаете
По списку доступных операций. Просто одна и та же операция может иметь разный интерфейс.
Взять даже очередь — кто-то назовёт функцию добавления в конец очереди push, кто-то rpush, кто-то add, кто-то put, кто-то epush и т. д. Названия разные, но делают эти методы одно и то же. Это не значит, что если мы назовём метод add вместо push, это перестанет быть очередью. По-моему, это очевидно.
Также частично учитывается и внутренняя структура. Но не реализация один в один: на чём реализован двусвязный список, на обычных выделениях памяти или на массиве — не имеет разницы. Но если мы вдруг начнём внутри поддерживать операции, допустим, от сортированного множества, даже если мы не добавим их в интерфейс, это уже будет не совсем двусвязный список, т. к. мы его сильно прокачали. Хотя частично это останется и двусвязным списком тоже.
Впрочем, если все улучшения будут сделаны именно для операций от двусвязного списка, наверное, это всё-таки останется двусвязным списком (но одновременно может быть и чем-то новым, например, одновременно деревом).
Также можно воспользоваться Википедией. Структура данных — это:- Либо абстрактный тип данных, где тип данных определяется поведением с точки зрения пользователя данных, а именно в терминах возможных значений, возможных операций над данными и поведением этих операций. Вот это определение похоже на моё.
- Либо реализация какого-либо абстрактного типа данных. Тут уже имеется конкретная реализация. Но реализаций может быть несколько. Это определение тоже совпадает с моим, т. к. код, который написал автор, я тоже считаю структурой данных (хоть это и немного противоречит русскому языку,
т. к. это код, а не структура). - Либо экземпляр типа данных, например, конкретный список. Не соответствует ни моему, ни вашему пониманию, но логично, т. к. в экземпляре данные находятся в определённой структуре, значит их можно назвать структурой данных.
- Либо в контексте функционального программирования — уникальная единица (англ. unique identity), сохраняющаяся при изменениях.
Вашего понимания там нет. А моё есть, т. е. я всё-таки не ошибся, хоть и говорил по интуиции.
Также можно воспользоваться определением Связного списка:
Связный список — структура данных, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка.
Реализация автора попадает под это определение (по крайней мере если её дописать, т. к. это прототип).
khim
19.12.2019 14:37+2Например, можно хранить номер элемента по ссылке. При физическом перемещении элементов менять этот номер. Все остальные куски кода будут получать уже новый номер мгновенно.
Во-первых — сделайте (я вот нифига не монимаю как вы собрались «мгновенно» что-то менять в итераторах, доступа к которым у вас нет).
Это только самый простой пример, можно сделать и лучше.
Во-вторых — это уже не будет тем, что описывал топикстартер.Вашего понимания там нет.
Серьёзно? А вот это вот что тогда:Реализация какого-либо абстрактного типа данных;
Реализация автора попадает под это определение (по крайней мере если её дописать, т. к. это прототип).
Ну так допишите, блин. Получите одно из двух: ваша стратура будет либо дико транжирить память (после добавления в структуру миллиона элементов и удаления всех, кроме первого и последнего вы всё равно будете тратить память на хранение их всех — иначе «протухнут» указатели на первый и последний элемент), либо в ней список нельзя будет развернуть за O(1) (даже XOR-список не даст этого сделать — опять-таки из-за хранения итераторов «где-то ещё»), либо, ещё будут какие-нибудь проблемы. Например если в одном массиве расположить несколько списков — то нельзя будет развернут один из них, можно только все сразу…

vitaliy2
20.12.2019 14:59-1я вот нифига не монимаю как вы собрались «мгновенно» что-то менять в итераторах, доступа к которым у вас нет
Я же привёл самый простой пример — хранить номер по ссылке.
Допустим в ячейке у нас лежал номер 5. Итератор хранил указатель на ячейку памяти, где лежит число 5. Во время итерирования 5-й элемент и 2-й поменялись местами. Пишем в эту ячейку памяти число 2 (ссылка на ячейку должна быть сохранена внутри двусвязного списка тоже).
Всё. В следующий раз, когда итератор обратится к этой ячейке, там уже будет число 2. При этом сам указатель не меняется, меняется только значение, которое лежит по этому указателю. Указатель выделяется с помощью стандартного менеджера памяти, например, средствами языка. Все указатели для одного и того же элемента равны (т. е. ссылаются на одно и то же место в памяти).
По поводу расхода памяти — да, это увеличит расход. Но даже 100 тыс элементов могут потратить, к примеру, только 1.2 МБ лишней памяти.
1 тыс элементов — 12 КБ. Вероятно, можно сократить до 8.Серьёзно? А вот это вот что тогда:
Имеется ввиду конкретная реализация. Иначе связный список будет только один во всём мире, т. к. если даже 1 символ кода бы отличался, это уже был бы не связный список.
Реализация какого-либо абстрактного типа данных;либо дико транжирить память
Не будет. Объяснил выше (хотя думал, это итак очевидно).либо в ней список нельзя будет развернуть за O(1)
Можно, автор же показал как.
Но придётся на каждый элемент, к примеру, хранить указатель на ячейку, где лежит номер для итерирования, что может занимать 4–8 + 4 байта на каждый элемент.

khim
20.12.2019 18:02Всё. В следующий раз, когда итератор обратится к этой ячейке, там уже будет число 2.
Нет, там не будет чисто 2. Там всё, что угодно может быть, так как после удаления мы ещё и добавить элементы можем, знаете ли.По поводу расхода памяти — да, это увеличит расход. Но даже 100 тыс элементов могут потратить, к примеру, только 1.2 МБ лишней памяти.
Там появятся новые телодвижения, новая деятельность. И, с огромной вероятностью, какая-нибудь ещё операция, которая обычно бывает в O(1) у вас станет более дорогой.Объяснил выше (хотя думал, это итак очевидно).
Как может быть очевидно то, что неверно?
Пока что вся дискуссия выглядит так: в ответ на ваше очередное «очевидное» предложение кто-нибудь объясняет, что оно — работать не будет. Вы добавляете ещё один костыль — после чего оно всё равно не работает — но уже по-другому.
Вообще же вся эта история напоминает старую цитату Энтони Хоара: There are two methods in software design. One is to make the program so simple, there are obviously no errors. The other is to make it so complicated, there are no obvious errors. (Существует два подхода к дизайну ПО. Один заключается в том, чтобы сделать программу настолько простой, что в ней, очевидно, не будет ошибок. Другой — сделать её настолько сложной, чтобы в ней не было очевидных ошибок.)
Вот вы явно — мастер второго подхода… но я вот совершенно не уверен в том, что вы сможете в принципе довести вот то самое «очевидное гуано», в которое превратилось уже изначальная конструкция из статьи в что-то хотя бы близко похожее на двусвязный список, а главное — у меня совершенно нет уверенности что полученное «гуано» будет хоть когда-то хоть в чём-то превосходить очевидную реализацию.Но придётся на каждый элемент, к примеру, хранить указатель на ячейку, где лежит номер для итерирования, что может занимать 4–8 + 4 байта на каждый элемент.
Ну вот сделайте, хотя бы, std::list интерфейс, а дальше уже можно будет что-то обсуждать.
Потому что пока что каждый раз когда вас макают лицом в ваше «гуано» в нём, вдруг, появляется очередной костылик, про который в предыдыщих сообщениях — ни слова.
А мы ж тут говорим не о гуманитарном полёте мысли, а о том, что, как бы, надо бы конкретный код для конкретного компилятора, в конечном-то итоге, написать…

vitaliy2
20.12.2019 19:46-1Нет, там не будет чисто 2. Там всё, что угодно может быть, так как после удаления мы ещё и добавить элементы можем, знаете ли.
Вероятно, Вы абсолютно не поняли, что я делаю.
Если мы удалили какой-то другой элемент, тут всегда будет лежать 2. Этот кусок памяти для хранения этого числа выделен не на нашем массиве, а стандартными средствами языка. Таким образом, даже несмотря на то, что обычные элементы постоянно меняют своё расположение в массиве, это число будет находиться всегда в одной и той же области памяти.
Именно за счёт этого итерирование будет происходить успешно. Т. к. мы никогда не перемещаем это число в другое место. Но при перемешивании элементов можем заменить на другое число, но в том же самом месте.сделайте std::list
Сразу говорю: я не привязываюсь ни к каким конкретным интерфейсам.
Я уже говорил ранее, что от того, что мы, к примеру, переименуем метод, у нас структура данных не превратится в другую.
Реализация конкретного интерфейса — это уже прихоть программиста. Интерфейсы в деталях, естественно, будут отличаться друг от друга. Главное, чтобы они выполняли одни и те же операции.
Естественно, это относится и к интерфейсу итератора. Я рассуждаю в терминах итераторов вообще, а не реализации в каком-то языке программирования. Языков много. И даже в пределах одного языка обычно может быть сразу несколько популярных вариантов реализации и много менее популярных.И, с огромной вероятностью, какая-нибудь ещё операция, которая обычно бывает в O(1) у вас станет более дорогой.
Разумеется, удаление и вставка станут работать немного дольше, но так и останутся O(1).Вы добавляете ещё один костыль — после чего оно всё равно не работает — но уже по-другому.
Вы даже не понимаете, как работают ссылки в языках программирования, и говорите, что не работает. Я объяснил достаточно просто алгоритм. То ли Вы просто тупите (что иногда у всех бывает), то ли не знаете принцип работы ссылок.Вот вы явно — мастер второго подхода…
Нет. Вы сказали, что это не двусвязный список просто лишь потому, что он реализован на массиве. Я лишь сказал, что нет, это двусвязный список. Если мы говорим о выборе реализаций для проекта, нужную реализацию я выберу исходя из требований. Чаще всего достаточно самого простого списка.Потому что пока что каждый раз когда вас макают лицом в ваше «гуано» в нём, вдруг, появляется очередной костылик, про который в предыдыщих сообщениях — ни слова.
Мда. Мы о чём спорили то. Приведите хоть одно доказательство то уже наконец, что это не двусвязный список.
Лично я могу привести свои:
Вставка — O(1)
Удаление — O(1)
Обход — O(n)
Ни одна из операций не обладает никакими проблемами. В т. ч. обход или итерирование.каждый раз когда
Вы так ни одного рабочего аргумента не привели. Это не похоже на «каждый раз».надо бы конкретный код для конкретного компилятора, в конечном-то итоге, написать
Вопрос был, является ли это двусвязным списком. Код для этого не нужен вообще, достаточно описание алгоритма. Привязки к конкретному языку программирования тоже не нужно. Поэтому реализация не нужна, и даже может быть вредна из-за привязки к определённому языку.

khim
20.12.2019 21:22+1Таким образом, даже несмотря на то, что обычные элементы постоянно меняют своё расположение в массиве, это число будет находиться всегда в одной и той же области памяти.
Замечательно. То есть для каждого элемента у вас будет ещё один «теневой элемент», указываеющий на ваш элемент? И ещё отсылка с «основного» элемента на теневой? Три ссылки вместо одной? И кто-то будет после этого разговаривать о кеш-линиях?
Вам не кажется, что ваша конструкция стремительно удаляется как от того, что описано в статье, так и от концепции «двусвязного списка» в принципе? А эффективность всей конструкции всё так же стремительно падает?Я уже говорил ранее, что от того, что мы, к примеру, переименуем метод, у нас структура данных не превратится в другую.
Да, но нет. Если у вас та же самая структура — то у вас не должно возникнуть сложностей с тем, чтобы переименовать методы обратно. Если же у вас с этим возникают проблемы — то это и значит, собственно, что вы реализовали какую-то другую структуру.Главное, чтобы они выполняли одни и те же операции.
И вот с этим — у вас пока проблемы.И даже в пределах одного языка обычно может быть сразу несколько популярных вариантов реализации и много менее популярных.
Конечно. Есть libstdc++, есть libc++, есть StlPort. Важно что они реализуют стандартный интерфейс, детали реализации могут и отличаться…Я объяснил достаточно просто алгоритм.
Извините — но вы, пока ещё, ничего не объяснили. Сказали что будет ещё одна ячейка для итератора — но не объяснили даже привязана ли эта ячейка к итератору или к элементу. Если к элементу — то у вас тут, невзначай, требования к памяти раза так в полтора-два выросли (а ведь автор статьи так заботился о кеше), а если к итераторам — то что вы будете делать, если итераторов будет много?Вы сказали, что это не двусвязный список просто лишь потому, что он реализован на массиве
Нет — я сказал, что это не двусвязный список потому что он не реализует ни интерфейса двусвязного списка (то есть не реализуется интерфейс соотвествующего АТД), ни повторяет реализацию (в этом случае до реализации интерфейса всё достраивается более-менее автоматически).
А тогда в каком именно смысле — это «двусвязный список»?Лично я могу привести свои:
Извините — но вы пока ещё даже не объяснили как у вас итерирование работает в сочетании со вставками и удалением. Что вы будете делать если у вас будет список на 1000 элементов и на него 1000 итераторов на каждый второй элемент? А как это вся конструкция работает если все 1000 итераторов указывают на один элемент — причём именно тот, который мы будем двигать?
Вставка — O(1)
Удаление — O(1)
Обход — O(n)
Ни одна из операций не обладает никакими проблемами. В т. ч. обход или итерирование.
А итерирование с параллельной модификацией списка — это, как раз, то, ради чего они обычно и используются.Код для этого не нужен вообще, достаточно описание алгоритма.
Вот только описания алгорима-то у вас и нет. Только размахивания руками и обвинения всех вокруг в том, что они идиоты.Поэтому реализация не нужна, и даже может быть вредна из-за привязки к определённому языку.
Извините — но вы сейчас чушь тут пишите. Если вы не можете реализовать ваш алгоритм на конкретном языке — то алгоритма у вас просто нет.
Недаром Кнут для рассмотрения алгоритмов использует даже не какой-то язык программирования, а прямо машинный код.
В некоторых случаях можно обойтись без написания кода — да… но для этого нужно, чтобы алгоритм был нормально описан. У вас же нет ни нормального описания, ни кода. Да и вообще не факт, что есть полное понимаете того, что вы пытаетесь выдать за «двусвязный список» — ясно только что ваша гипотетическая структура имеет мало общего с описанной в статье…

vitaliy2
21.12.2019 12:30-1И кто-то будет после этого разговаривать о кэш-линиях?
Вообще тут наконец Вы правы.
Хотя если список не изменяется, можно сделать простой обход без обращения к моим дополнительным указателям и получить полную выгоду от кэшей. Обращение нужно только при изменении списка.
Но наконец Вы сказали что-то аргументированное =)Да, но нет. Если у вас та же самая структура — то у вас не должно возникнуть сложностей с тем, чтобы переименовать методы обратно.
Названия методов я привёл только как пример.
Например, в JS обход чего-либо с длиной можно сделать с помощью for (let i = 0; i < a.length; i++), а можно с помощью for (const value of a). Оба этих варианта реализуют обход за O(n) (обычно), но интерфейс разный, и реализация тоже.
При этом ни в коем случае нельзя сказать, что если мы вдруг вместо одного варианта реализуем другой, это перестанет быть этой структурой данных.И вот с этим — у вас пока проблемы.
Где? Пример в студию =)
Я Вас похвалил за аргумент вначале, но это касалось только коэффициента производительности, сложность так и осталась O(1).Конечно. Есть libstdc++, есть libc++, есть StlPort. Важно что они реализуют стандартный интерфейс, детали реализации могут и отличаться…
Я имел ввиду, что они могут реализовывать не «стандартный» интерфейс в этом языке, а вообще разные интерфейсы.то у вас тут, невзначай, требования к памяти раза так в полтора-два выросли (а ведь автор статьи так заботился о кэше)
Дополнительная ссылка на каждый элемент, а не итератор. Я уже ответил выше — если во время обхода список не изменяется, можно использовать более простой обход, который будет эффективно использовать кэш.
В противном случае придётся делать обход с полурандомными обращениями к памяти, откатываясь к производительности обычного списка.не реализует ни интерфейса двусвязного списка, т. к. не работает норм итерирование
Ответил, но отвечу ещё раз: ссылка на элементы, а не итераторы (как Вы подумали), поэтому всё норм.
На следующие 3 Ваших ответа ответ такой же, т. к. Вы писали их с учётом того, что подумали, что дополнительные ссылки будут на итераторах.чтобы алгоритм был нормально описан
Достаточно просто сказать, что мы добавляем указатели на элементы, чтобы итерирование не сломалось и все операции работали за O(1).
Хотя даже это можно было не говорить — изначально итак понятно, что легко сделать итерирование нормально. Но я сказал.
По поводу Кнута — естественно, если бы я писал книгу, а не комментарий на каком-то сайте, то объяснил бы намного подробнее. Но это не книга, поэтому очевидные вещи объясняться не будут, предполагается, что читатель итак понимает их изначально. Но Вы не поняли.

khim
21.12.2019 19:25+2Но это не книга, поэтому очевидные вещи объясняться не будут, предполагается, что читатель итак понимает их изначально. Но Вы не поняли.
потому что предполагалось, что я общаюсь с нормальным человеком, не идиотом, который «за базар» отвечает.
С чего вся дискуссия началась, напомнить? Я могу:Список из статьи удовлетворяет этим условиям.
Извините, но ваша конструкция вот ни разу не похожа на то, что описано в статье.
Похоже на то, как если бы кто-то попытался решать проблему разворота автомобиля на месте путём откручивания от него колёс — а когда, после долгих разговоров и объяснений, что после такого действия автомобиль просту упадёт на дорогу — выяснилось бы, что «на самом деле» вы обсуждаете автомобиль с открученными колёсами, но при этом подвешенным под мостовым краном на тросе.
Извините — но эта конструкция это просто верх идиотизма. Да, создать её возможно… но зачем? Тут сразу вспомнинается картинка про троллейбус из буханки хлеба.Дополнительная ссылка на каждый элемент, а не итератор. Я уже ответил выше — если во время обхода список не изменяется, можно использовать более простой обход, который будет эффективно использовать кэш.
Не будет он эффективно использовать кэш. Потому что «прыжки» всё равно сохранятся. Эффективно вы сможете только лишь пройти весь массив, где у вас элементы лежат. И вы забыли про ещё один массив — со ссылками от элементов «к теневым указателям». Без них всё это работать не будет.
Однако есть у всей этой конструкции «фатальный недостаток»: все эти массивы в этой конструкции — лишние. Гораздо проще выкинуль все эти индексы и прочее и взять простоstd::list<int*, SpecialAlloc>— гдеSpecialAllocбудет выделять элементы в массиве, хранить в другом массиве ссылки итератор для этого самого списка и при удалении — делатьswap. И, собственно, всё — получим всё что умеет ваш «мостовой кран с подвешенным левитирующим автомобилем» за вычетом дурацких, никому не нужных тросов.
А если хотите ещё и разворачивать за O(1) — ну добавьте булевский флаг к этому всему… хуже всё равно уже не будет.

vitaliy2
22.12.2019 13:02Не будет он эффективно использовать кэш. Потому что «прыжки» всё равно сохранятся. Эффективно вы сможете только лишь пройти весь массив, где у вас элементы лежат. И вы забыли про ещё один массив — со ссылками от элементов «к теневым указателям». Без них всё это работать не будет.
Вы не поняли. Этот дополнтельный массив с теневыми указателями нужно использовать, только если во время обхода есть удаление элементов.
Если удаления нет, массив можно не использовать, и никаких прыжков не будет.
Т. е. будет два способа обойти список — один быстрый, и другой более медленный.Извините, но ваша конструкция вот ни разу не похожа на то, что описано в статье.
В статье прототип. То, что я мысленно дополнил его — это уже придирки.
Да, чисто формально конструкции разные. Но это придирки, т. к. зачем автору статьи прорабатывать детали, особенно если большинству они итак понятны. Их нужно просто мысленно представить.создать её возможно… но зачем?
Это совсем другой вопрос. Может и незачем. Но мы ведь не это обсуждали.
Но если отвечать на него, то на практике да, такая конструкция редко нужна. Но я и не говорил, что это не так.

khim
22.12.2019 16:08В статье прототип.
Серьёзно? Вы правда верите что автор «имел в виду» вот эти вот дополнительные построения, два типа итераторов и прочее?
Как-то я ну очень сильно сомневаюсь.Но это придирки, т. к. зачем автору статьи прорабатывать детали, особенно если большинству они итак понятны.
Большинству — они непонятны. Натурный эксперимент показал. Если для вас «большинство — это группа людей, в которую вхожу я» (и неважно что вас двое, а в другой группе — 100 человек), то у меня для вас плохие новости.Это совсем другой вопрос. Может и незачем. Но мы ведь не это обсуждали.
А что мы тогда, извините, обсуждали? Любая структура данных (в программе или где-либо ещё) ведь создаётся не просто так — а для решения определённых задач.
И в тот момент, когда вы пристроили к «машине бес колёс» кран (== добавили «теневые» элементы, которые нужно поддерживать в рабочем состоянии всегда и память на них тратить всегда) — вы получили другую структуру данных. С другими свойсвами.Этот дополнтельный массив с теневыми указателями нужно использовать, только если во время обхода есть удаление элементов.
То есть у нас теперь есть «быстрые итераторы», «медленные итераторы» и вообще чёрт знает что. Но время и память на поддержание «теневых списков» мы тратим всегда (иначе у нас O(1) для «медленного»beginне получится).
Жуть какая. Я бы эту структуру «двусвязным списком» не назвал. Это больше похоже на его эмуляцию. То есть снаружи — да, немного похоже (хотя и менее эффективно), но внутри… «индусский код» напоминает.b.toString() == "false"для булевского типа. А что? Тоже ведь O(1).

vitaliy2
22.12.2019 17:36А что мы тогда, извините, обсуждали?
Мы обсуждали не полезность, а является ли это двусвязным списком.индусский код
Если мы уж начали говорить на эту тему, то изначально разворот списка за O(1) не нужен. Тут у автора был спортивный интерес.
Я не буду спорить, что это, возможно, индусский код. Я бы и сам не поюзал такую структуру, т. к. она редко нужна (только если списки очень большие, очень сильно важна производительность, часто делаются обходы и при обходах не делаются удаления — соблюдение всех этих условий редкая вещь).
Я уже написал выше, процитирую ещё раз:Но если отвечать на него, то да, на практика такая конструкция редко нужна. Но я и не говорил, что это не так.
и память на них тратить всегда
Трата памяти обычно критична только если важна производительность кэшей, размер которых ограничен.
Здесь же дополнительные указатели практически никогда не будут использоваться, т. к. человек, которому нужно удалять элементы внутри обхода, изначально не будет использовать описанную структуру. А вот при обходе без удалений данная структура будет работать быстрее за счёт кучности.
Как итог, здесь производительность кэшей не ухудшается. Остаётся только обычный расход памяти, но это некритично. Даже огромный список из 100 тыс элементов может потратить чуть больше мегабайта лишней памяти. Пользователь с 32 ГБ памяти сможет запустить 22 тыс таких программ. Не тот случай, когда нужно париться о памяти.

khim
22.12.2019 18:00Мы обсуждали не полезность, а является ли это двусвязным списком.
Только вот это — это то, что описано в статье, а не то, что вы тут наизобретали.
Можно говорить о том, то автор что-то недописал (скажем у него нет функции удаления), но когда мы начинаем добавлять дополнительные конструкции (ваши «теневые» ссылки от из связи с основным списком) и менять (причём существенно менять), то что там описано — то это перестаёт быть «тем что описано в статье» и начинает напоминать обсуждление цвета травы на известной картине. «Корова на лугу есть траву». Помните? Там где траву сьела корова и ушла.
Вот и у нас тут примерно то же самое — какие-то воображаемые дополнительные элементы (о которых в статье ни слова), перевыделение памяти (которого там тоже нет) и т.д. и т.п.
Вот только в статье про кэши говорилось совершенно явно — в отличие от «теневых ссылок», которых там нет.и память на них тратить всегда
Трата памяти обычно критична только если важна производительность кэшей, размер которых ограничен.
Здесь же дополнительные указатели практически никогда не будут использоваться
Извините, но у вас нет выбора. Если вы не бужете поддерживать вашу теневую строктуру «в рабочем состоянии» при добавлении и удалении элементов, то вы не выдержите обещанные O(1) для операций с «медленными» итерторами. То есть вы вынуждены добавлять код даже в те функции, которые явно прописаны в статье и тратить память — даже если вы ни разу «медленные» указатели не используете.Не тот случай, когда нужно париться о памяти.
Если бы автор не говорил о кэш-линиях, тогда да. Но он говорит. То есть нас интересуют уже не 32GiB нафантазированной вами памяти, а вовсе даже 32-64KiB кеша L1. Заметим, что это число вообще никак со временем не меняется: как появился 32KiB кеш четверть века назад — так он и сегодня в 32KiB. Иногда увеличивают до 64KiB (многие процессоры AMD), потом всё равно назад откатывают (в Zen2 опять вернулись от 64KiB к 32KiB).

vitaliy2
22.12.2019 18:18Извините, но у вас нет выбора. Если вы не бужете поддерживать вашу теневую строктуру
Я имел ввиду случай, когда у нас часто выполняется обход (без удаления), но нечасто удаление, а также добавление элементов.
Я так и написал, что в таком случае список будет работать быстрее, а в других медленнее.Вот только в статье про кэши говорилось совершенно явно
Да. Перечитайте, что я написал выше. Кэши действительно будут использоваться эффективнее, чем в стандартном алгоритме, если много обходов без удаления и мало остального.
В противном случае кэши будут использоваться менее эффективно.Не тот случай, когда нужно париться о памяти.
Вы снова неверно прочитали моё сообщение.
Если бы автор не говорил о кэш-линиях, тогда да
Цитирую:Как итог, здесь производительность кэшей не ухудшается.
…
Не тот случай, когда нужно париться о памяти.
а также:Трата памяти обычно критична только если важна производительность кэшей, размер которых ограничен
В данном случае нам удаётся использовать лишнюю память, не оказав негативного воздействия на кэши (когда мало удалений и добавлений, но много обходов без удалений). Это достигается за счёт того, что при обходах без удаления к этим теневым ссылкам даже не будет никакого обращения.
Раз нет обращения к памяти, значит нет и негативного влияния на производительность кэшей.

khim
22.12.2019 18:55Я имел ввиду случай, когда у нас часто выполняется обход (без удаления), но нечасто удаление, а также добавление элементов.
В этом случае, как я уже писал, выгоднее выкинуть все эти дополнительные связи (оставив их для добавления/удаления) и просто обходить массив где лежат все элементы.Кэши действительно будут использоваться эффективнее, чем в стандартном алгоритме, если много обходов без удаления и мало остального.
Однако ещё эффективнее они будут использоваться в том случае когда мы будем использовать обычный список, указывающий на элементы в массиве.
Вообще при обсуждении структур я обычно стараюсь придерживаться того же принципа, что и создалени C++: конструкция должна быть расширяема, но не изменяема.
Ну просто потому что если вы разрешаете изменять что-то без ограничений — то уже становится неясно чем дерево отличается от списка и от вектора…
Вы же неявно, но существенно, изменили функции которые явно приведены в статье — отсюда вся путаница.
В сухом остатке:
1. Мне и для структуры-то описанной автором статьи не удаётся придумать задачу, где на была бы полезна, а для этой вашей странной конструкции — так и подавно.
2. То что описано в статье и то что наворотили вы — это существенно отличные вещи.
И вот пункт #2 тут, на само деле, гораздо важнее пункта #1.

mSnus
17.06.2020 00:25Ох, почитал ваши диалоги и стал образованнее на 3 левела. Спасибо, люблю Хабр за это.

khim
17.06.2020 23:25Хабр — это одно из редких мест, где достаточно много спорщиков стараются установить истину. Не всегда это получается, но попытки есть.
На большинстве же сайтов подавляющее большинство участников спорят, чтобы «почувствовать себя хорошо». Истину они уже «познали» (ну или им так кажется), осталось только «чужаков» «комками грязи закидать» — и дело сделано.

playermet
19.12.2019 23:00А причём тут интерфейс?
При том что автор утверждает что «все что выглядит как список — список». Но даже если взять двусвязный список и представленную структуру данных с идентичными сигнатурами методов при замене первого на второй начнут возникать ошибки. Потому что первому не нужно чинить итераторы, а второму — нужно.Вроде, да. На удаление это не влияет
Увы, но нет. Модификация добавляющая чанки автоматом меняет сложности и создает необходимость в обработке ситуаций которых раньше не было.
Даже о вставке за O(1) можно забыть, потому что теперь возникает необходимость пробегать по чанкам в поиске свободной позиции. Т.е. если capacity 100 элементов, у нас миллион элементов, и все чанки кроме последнего заняты, то для вставки в конец нужно будет пробежаться по всем десяти тысячам чанков. Можно конечно увеличить capacity, но тогда усугубятся проблемы с перерасходом памяти. В любом случае, асимптотика уже другая.
И на удаление это еще как влияет, потому что теперь нужно удалять и сами чанки. А тут может возникнуть отдельная веселуха — если удалять чанк как только он опустеет то может возникнуть ситуация, когда зацикленная вставка и удаление одного элемента вызывает аллокацию и освобождение памяти под полный capacity дополнительного чанка. А исправление этой ситуации означает хранение пустого чанка когда он возможно и не нужен.Связный список тут не при чём.
Как это не при чем? Возможность манипуляций (джойн, сплит, и т.д.) над связными списками за O(1) это одно из их важных свойств.Думаю, Вы не так поняли алгоритм автора.
Во-первых я уверен что понял все правильно. Во-вторых структура данных автора не реализует ни чанков, ни удаления элементов, ни других операций, их вы сейчас мысленно добавили сами, автор тут не при чем. А в-третьих у списка с чанками сложность просто не может быть как у двусвязного списка, так же как нельзя отсортировать сравнениями быстрее чем за O(nlogn). Про сложность по памяти вообще молчу, там будет ад — n*capacity памяти под n элементов в худшем случае.
vitaliy2
20.12.2019 20:12-1Даже о вставке за O(1) можно забыть
Асолютно неверно.
У нас все чанки уплотнённые. Поэтому пробегать чанки не нужно, вставка возможна только в конец, других мест просто нет, они заняты.
Это достигается за счёт того, что при удалении элемента из середины на его место перемещается последний элемент. Таким образом, дырок нет.Потому что первому не нужно чинить итераторы, а второму — нужно.
Есть конкретная реализация интерфейса, и если нужна её поддержка, её да, вероятно, придётся чинить.
А есть просто список поддерживаемых операций. Например, мы говорим, что нам доступна операция вставки за O(1), но не говорим, как именно надо будет производить её, а уж тем более название метода.
Когда мы хотим охарактеризовать структуру данных, используется второй подход. Потому что иначе было бы глупо, что если мы вдруг назвали метод push, а не add, то это уже стало бы не списком. Понятное дело, что решения о конкретном интерфейсе останутся за программистом.И на удаление это еще как влияет, потому что теперь нужно удалять и сами чанки.
Свободными могут быть только последние чанки. Как только стало 2 полностью свободных чанка, удалить один, и всё.
Работает это за O(1).
Цикл со вставкой и удалением тоже ничего не испортит вообще, т. к. мы не будем удалять чанк сразу после освобождения, а только когда освободится ещё один чанк или, к примеру, половина чанка.Как это не при чем? Возможность манипуляций (джойн, сплит, и т. д.) над связными списками за O(1) это одно из их важных свойств.
Первый раз слышу об обязательной поддержке этих операций. Они идут как бонус.
Но даже если бы требовалось, то всё-равно никаких проблем с указанными Вами операциями за O(1) тут не вижу. Правда копирование списка за O(1) не сделать, но это относится и к обычному списку.
Чтобы сделать копирование за O(1) надо использовать персистентный связный список.А в-третьих у списка с чанками сложность просто не может быть как у двусвязного списка, так же как нельзя отсортировать сравнениями быстрее чем за O(nlogn). Про сложность по памяти вообще молчу, там будет ад — n*capacity памяти под n элементов в худшем случае.
Надеюсь, когда Вы перечитываете это после моего комментария, смеётесь =))))))
Вообще говорить «невозможно» просто основываясь на интуицию опасно, т. к. она часто подводит. И ещё ненаучно, т. к. утверждение такое требует доказательств, которые зачастую очень тяжело или невозможно отыскать. Хотя в математике часто доказывают невозможность вещей. Но это сложнее, чем доказывать возможность. И там доказывают строго.
khim
20.12.2019 21:32Это достигается за счёт того, что при удалении элемента из середины на его место перемещается последний элемент. Таким образом, дырок нет.
Если дырок нет — то нет и двусвязного списка. Потому как это его основное свойство: вы можете удалять из него элементы по одному, а все остальные — остаются доступными по тому же адресу. Ваше предложение завести наряду с вашим замечетльным «специальным» списком рядышком ещё один, теневой, обычный — нигде в статье не описано и я очень сомневаюсь, что автор статьи имел в виду именно это.Например, мы говорим, что нам доступна операция вставки за O(1), но не говорим, как именно надо будет производить её, а уж тем более название метода.
Дык вопрос не в названиях. Вопрос в том, как вы собираетесь делать удаления и вставки без инвалидации итераторов. И неважно: называете вы итераторы «указателями», «ссылками» или, как в C++ итераторами — семантика двусвязного смысла такова, что они не «протухают» если другие элементы удаляются или вставляются.
Чего у автора в статье нет и в поминие, извините.Цикл со вставкой и удалением тоже ничего не испортит вообще, т. к. мы не будем удалять чанк сразу после освобождения, а только когда освободится ещё один чанк или, к примеру, половина чанка.
C «теневым списком» вы что собрались, при этом, делать?Вообще говорить «невозможно» просто основываясь на интуицию опасно, т. к. она часто подводит.
Тем не менее когда этим же занимаетесь вы — то все должны вам верить наслово. Откуда двойные стандарты?

vitaliy2
21.12.2019 12:42C «теневым списком» вы что собрались, при этом, делать?
Ничего, за ним следят стандартный менеджер памяти и сборщик мусора (если есть).

playermet
20.12.2019 23:54Таким образом, дырок нет.
Но у вас ведь джойн списков «без проблем реализованный за O(1)». А значит копирования элементов между чанками при джойне нет. А значит неполные чанки остаются неполными, и образуют дырки в середине. Вы уже сами запутались что там у вас и как должно быть реализовано.Потому что иначе было бы глупо, что если мы вдруг назвали метод push, а не add, то это уже стало бы не списком
Имена методов тут вообще не при чем. У операций двусвязного списка и вашего винегрета отличается семантика, а потому это фактически разные операции. А поэтому уже не важно какие будут выбраны имена, эта структура не является двусвязным списком даже в контексте АТД.Надеюсь, когда Вы перечитываете это после моего комментария, смеётесь
Так и есть, но повод у этого смеха явно не тот что вам кажется.Вообще говорить «невозможно» просто основываясь на интуицию
Интуиция здесь не при чем, это закон сохранения энергии. Нельзя получить что-то не пожертвовам чем-то другим, если только изначальная версия не содержит избыточного кода (а она не содержит). А потому я еще раз повторю, вы не сможете получить на представленной структуре данных сложностей двусвязного списка. Вам придется пожертвовать частью его свойств, чтобы реализовать другие.

vitaliy2
21.12.2019 12:40-2Но у вас ведь джойн списков
Ага, это проблема. Чтобы не было дырок, придётся тогда хранить все списки в одном массиве чанков. Но тогда потеряем производительность кэшей. А раз так, смысла в этом сложном списке никакого. Если только не юзать джойн.У операций двусвязного списка и вашего винегрета отличается семантика
У каких именно? Я сказал выше, что смысла никакого, но это не делает его не двусвязным списком, а просто убирает смысл в его существовании.
Хотя и джойн списков не является обязательной операцией. Насколько я знаю, обязательные вставка в любое место за O(1), удаление за O(1), обход за O(n) и возможность получения следующих и предыдущих элементов от любого за O(1).
Все данные 4 операции поддерживаются.

playermet
23.12.2019 22:34Чтобы не было дырок, придётся тогда хранить все списки в одном массиве чанков
Дыры в чанках можно убрать только переносом в эти самые дыры элементов из других чанков. А это уже O(capacity) при джойне. Либо так, либо O(n) при вставке.Если только не юзать джойн.
Важен не сам джойн, он тут просто для примера. Важно то что у двусвязного списка есть определенные свойства, за счет которых существует возможность реализации таких операций как джойн/сплит/т.д. за O(1). Представленная структура данных эти свойства нарушает.У каких именно?
У тех которые ломают итераторы. Код в котором двусвязный список заменен этой структурой будет вести себя иначе, а это и есть «иная семантика». При этом модификации которые чинят итераторы привносят свои собственные проблемы, делающие саму структуру нецелесообразной. И это я еще не касался такой типичной особенности двусвязных списков, как неизменность адреса элемента в памяти.

khim
24.12.2019 02:13И это я еще не касался такой типичной особенности двусвязных списков, как неизменность адреса элемента в памяти.
Я коснулся. В качестве решения было предложено завести ещё один список (уже более-менее обычный) с дополнительными отсылками от него на элементы вот этого вот «оптимизированного» списка. И обратно.
При этом мне объяснялось, что это — вот именно то, что имел в виду автор. Вот эта вот куча ссылок в разные стороны, аллоцируемые отдельно элементы, но, в добавление к ним — ещё и элементы в массивы… вот это вот всё, оказывается — было частью задумки… просто это было «очевидно».

vitaliy2
24.12.2019 13:57Дыры в чанках можно убрать только переносом в эти самые дыры элементов из других чанков.
Нет. Если всё хранить в одном массиве чанков, дыр изначально не будет.
При удалении будет всегда переноситься 1 последний элемент из последнего чанка.

khim
24.12.2019 16:09+1Если всё хранить в одном массиве чанков, дыр изначально не будет.
Если хранить всё в одном массиве чанков, то вы не сможете «развернуть список» за O(1) — а это было одним из условий в статье.

vitaliy2
24.12.2019 16:38Если хранить всё в одном массиве чанков, то вы не сможете «развернуть список» за O(1) — а это было одним из условий в статье.
Разумеется, имелся ввиду один массив чанков для каждого из направлений, суммарно два массива чанков. Можно добавить и третий для более быстрой отработки некоторых операций (и более медленной других). Элементы в них будут на одинаковых позициях, поэтому всё норм.

CorvOrk
16.12.2019 14:27Тут дело в том, что двусвязанный список не оперирует индексами, он использует связи. Все удобство и все свойства двусвязанного списка заключаются в использовании узла, который знает о соседних узлах, которые в свою очередь могут находиться в памяти где угодно. В Вашем случае у меня, например, есть объект D — но я не могу просто использовать этот объект D для работы, я обязан отобразить его на индекс, который скажет, где он располагается в data (struct node { size_t index; }) — это все к тому, что предложенная структура не является double linked list. Структура это не просто интерфейс, важно ее устройство.
Проблема дыр — это основная проблема Вашего способа — простое запоминание индексов дыр тут не поможет — для быстродействия это ничто, но в плане памяти — нужно помнить обо всех дырах, что в случае большого capacity очень накладно.
Соответственно структуру лучше выбирать, когда известна задача — статья больше полезна для разминки мозгов, за что автору спасибо.
nshalimov Автор
16.12.2019 17:16+4Ответ на этот комментарий и на комментарий выше.
Тут дело в том, что двусвязанный список не оперирует индексами, он использует связи.
Именно связи. Связи != указатели. И указатели в принципе – это тоже индексы, смещение которых скрывает от вас контекст (рантайм). Здесь просто более явный контекст – конкрретный экземпляр DLL.
Все удобство и все свойства двусвязанного списка заключаются в использовании узла, который знает о соседних узлах, которые в свою очередь могут находиться в памяти где угодно.
Да, для данного конкретного юзкейса DLL предложенный вариант не подходит. Но не все так работают со списком.
Например такой сценарий: вам нужно просто получить данные, скажем, 2762 элемента списка. Вы просто итерируете 2762 раз вперед от начала (не подгружая ненужные поля) и забираете данные по индексу из массива с данными.
Для такого сценария предложенный вариант будет эффективнее.Структура это не просто интерфейс, важно ее устройство.
В том-то и дело, что устройство логически не поменялось, поменялся просто лейаут. Он из вертикального (AoS) превратился в горизонтальный (SoA). Мне очень часто приходится так делать, для разделения горячих и холодных данных, например.
Заметьте так же, что даже алгоритмы вставки в примере не так уж отличаются от примеров в той же википедии.Проблема дыр — это основная проблема Вашего способа — простое запоминание индексов дыр тут не поможет — для быстродействия это ничто, но в плане памяти — нужно помнить обо всех дырах, что в случае большого capacity очень накладно.
И тут я могу обойтись без дыр с помощью свопа из конца в удалённую позицию. Жертвуя валидностью итератора. Который, впрочем, я могу вернуть из метода удаления обновлённым и дейсвтительным.
Соответственно структуру лучше выбирать, когда известна задача — статья больше полезна для разминки мозгов, за что автору спасибо.
Всё, кроме этого вывода в статье – детали. Спасибо, что обратили внимание на главное

wataru
17.12.2019 00:24И тут я могу обойтись без дыр с помощью свопа из конца в удалённую позицию. Жертвуя валидностью итератора. Который, впрочем, я могу вернуть из метода удаления обновлённым и дейсвтительным.
Тут не надо даже свопа. В этих массивах можно хранить сразу несколько списков. Соответственно, в аллокаторе храните начало списка пустых элементов и максимально использованный индекс. Если нужно выделить элемент, берете его из списка пустых. Если список пуст — берете новый сначала неразмеченной области. При удалении элемента добавляйте его в список пустых.

InterceptorTSK
16.12.2019 15:39Автор, да скажите же уже банальность. :) Всё что есть — один фиг нынче хранится в куче, что и есть массив, который на самом деле множество. И куча отображается в это множество, вообще-то. Если полезть ещё дальше, то вся опиративка — это тоже множество. В которое что-то да отображается. И всё что есть — в любом случае куски этого множества. Ну а как вы представляете абстракции — это уже ваше дело. В принципе вы правы, если это снаружи выглядит для пользователя как список, ведёт себя как список – то это список и есть. Абстракции — это конечно же только и только абстракции. А как они реализованы — вообще не имеет значения. Впрочем, технически вы создаёте что-то действительно отличающееся от классического списка, потому что опять же технически оно будет чем-то большим, чем классический список, а значит это уже не список, а что-то другое. Однако же родительской абстракцией относительно вашей новой абстракции в данном случае будет классический список, плюс какие-то добавки, что собственно и отличает вашу новую абстракцию.
Почему будет что-то другое? Так это тоже банальность. Т.к. вы технически всё это дело организуете иначе, то и возможности появятся на что-то ещё. Это что-то ещё в принципе даст это самое отличие, которое не позволит вашей абстракции называться списком.

0xd34df00d
16.12.2019 19:35+3ведёт себя как список – то это список.
Оно не ведёт себя как список, так как те же гарантии сложности и инвалидации итераторов вы не получите. Впрочем, вам про это уже писали.
Да, вариант с чанками может помочь (но это ещё надо доказать), но это будет другая структура данных.
Плюс интепрпретация указателей в зависимости от состояния этого флажка – ещё один уровень перенаправления (level of indirection). В виде бранча (return is_reversed? link1: link2) или в виде взятия по индексу (return links[is_reversed]). Не сказал бы, что это решение будет «чище».
Бранч предиктор очень быстро научится это предсказывать. Да и в ряде случаев можно вынести это на уровень темплейтов, например, компилятор все свернет.

cher-nov
17.12.2019 01:37Можно по идее сделать и без дополнительной памяти. Так как двусвязный список обычно состоит не только из узлов, но и ещё структуры для хранения количества элементов и указателей на первый и последний узлы.
Тогда добавляем два условия:
- Адрес первого узла в памяти меньше, чем адрес последнего.
- Память под первый и последний узлы выделяется при создании списка и остаётся вплоть до его уничтожения.
В таком случае роль предлагаемого Вами бита будет играть сравнение указателей на первый и последний узлы. А роль его инверсии — обмен значений этих указателей.
Можно пойти дальше и отказаться от второго условия, выполняя первое не при создании списка, а при операциях добавления/удаления элемента.Другой вопрос, что в том же Си сравнение указателей, не являющихся частью одного объекта — это то ли неуточняемое (unspecified), то ли вообще неопределённое (undefined) поведение (behavior). В случае с двумя условиями это по идее можно обойти, выделяя память под оба узла одним вызовом
malloc(). А вот для случая с одним условием понадобится свой менеджер памяти (?), причём весьма специфичный. Например.Поправьте меня, если не прав.

RyDmi
16.12.2019 12:48+8Хорошее начало. Теперь жду разворот односвязного списка за О(1).

kryvichh
16.12.2019 14:13+7Взять двухсвязный список, и публиковать только ссылку First, и ссылки Next в узлах. Ну а далее, как написал автор чуть выше, [с моей добавкой]:
«Если это снаружи выглядит для пользователя как [односвязный] список, ведёт себя как [односвязный] список – то это [односвязный] список».

a5b
16.12.2019 19:19+1Или взять XOR-список https://en.wikipedia.org/wiki/XOR_linked_list (и хранить 2 ссылки входа в список)

somurzakov
19.12.2019 01:08это классический trade-off между дополнительной памятью (хранить дополнительные N ссылок) и быстродействием и именно к этому и подводит этот вопрос на техническом интервью при обсуждении реализации.
Классические вопросы от интервьювера: а теперь представь что двухсвязный список это список всех страниц в интернете или список белков в геноме, что-угодно большое и занимает огромное место и твой алгоритм не подойдет по требованиям памяти т.д. и т.п…
и если интервьювируемый может спокойно рассуждать об этом trade-off и менять свой алгоритм от медленного, но жрущего мало памяти, к более быстрому, но жрущему больше памяти, оценивать сложность алгоритма в О-нотации — то это говорит об определенном уровне зрелости и такого надо нанимать.
именно это и хочет увидеть интервьювер, а не просто самую популярную реализацию двойного списка из книги cracking the code interview которая лежит на первой ссылке в гугле на стековерфлоу

netricks
16.12.2019 12:49+5Вообще, идея упаковать элементы списка в массив и использовать индексы вместо указателей довольно древняя. Эта структура хороша как пул объектов, которые используются в виде списка. Например, так можно выделять объекты задач для диспетчера процессов.
Такой список с одной стороны имеет достоинство (он не фрагментирован), а с другой недостаток, поскольку, как тут заметили, свыше cap выделить память можно только если пул работает в страничном режиме, а индексы работают по принципу «страница-смещение».
Приём вынесения индексов next/prev за пределы пула объектов довольно интересен. Поскольку позволяет работать над индексами как отдельной сущностью без итерирования по коллекции. Спасибо. Сомнительно конечно, но это может быть полезным.
aamonster
16.12.2019 14:39+1Обычно эта идея реализуется сама собой, когда объекты уже лежат в каком-то массиве, и надо их просто связать между собой.
А за пределами такого применения односвязные/двусвязные списки не очень хороши (массив или массив/список массивов их рвёт по производительности).
dimkss
16.12.2019 12:52+10Ваша новая структура имеет свойства двусвязного списка?
Например удаление узла/добавление узла в любую точку списка за константное время?
vsb
16.12.2019 13:07+1Простой вариант: хранить данные "чанками", не слишком большими и не слишком маленькими, например по 64 байта. Чанк это просто массив + длина, а также ссылка на следующий чанк (ну и на предыдущий, если нужен двусвязный список). Для вставки или сдвигаем все элементы чанка, если в нём осталось свободное место, или создаём новый чанк с одним элементом и вставляем его, как в обычном списке. Для удаления тоже сдвигаем все элементы или удаляем весь чанк, если там ничего не осталось (тут желательно сделать оптимизацию и не просто удалять весь чанк, а проверять соседние и если они полные — делить элементы между ними, чтобы не попасть на патологический случай, когда идёт вставка/удаление в одно место и мы постоянно создаём/удаляем один чанк).
За счёт того, что чанк имеет фиксированный максимальный размер, асимптотическая сложность этих операций будет равна O(1). И с процессорным кешем такая структура будет хорошо сочетаться.

Lirein
16.12.2019 13:46+3Вы почти СУБД изобрели. Я подобную штуку делал для in-memory базы данных оперативно-расчетной подсистемы ОКО.
MacIn
18.12.2019 08:16Подобные структуры данных уже есть. Гуглится по «массив списков» или «список массивов». Как вариант — unrolled list.
Есть структура VList:
rosettacode.org/wiki/VList
В последней чанки разной длины с интересным обоснованием (длина изменяется двукратно в зависимости от того, куда «дороже» вставлять).

pvl_1
16.12.2019 13:09+1Я не автор, но, очевидно, да.
Пруф — работы по Structure Layout Optimizations и (в частности) Structure Peeling и Structure Splitting. То, что сделал автор, — как раз Structure Peeling в версии разрезания не на 2 структуры, а на раздельные поля, с обходом вопросов по корректности указателей после разрезания с помощью замены на индексы. Такого рода оптимизации обязаны сохранять логику использования, так как применяются в компиляторах.

nshalimov Автор
16.12.2019 13:22-3Да, конечно. Если вы не переполните капасити. Но на этот случай, например, подойдёт предложенный выше вариант с чанками.

a-tk
16.12.2019 13:26+7А что мешает иметь враппер поверх двусязного списка, который считает, что тот направлен в другую сторону?

GCU
16.12.2019 14:11+5А можно как-то более развёрнуто про кэш-линии?
В AoS допустим я каждый элемент промазываю, но при этом хотя-бы читаю значение элемента из кэша.
В SoA я точно так же промазываю, но уже целых два раза — для самого значения и ещё для указателя.
В чём профит?
khim
17.12.2019 03:20В том, что треть структуры вообще не загружается в память, если вам «в одну сторону» ходить.
А если нужно обработать все элменты (и неважно в каком порядке) — то ссылки не нужно загружать в память совсем.
Но вообще странное какое-то требование: если вам в одну сторону только и надо ходить — к вашим услугам односвязный список… хотя, конечно, чисто теоретически и вот под эту странную конструкцию можно задачу придумать… жаль только не наоборот… очень сложно себе представить не «высосанную из пальца», а реальную задачу где что-нибудь одно (массив, односвязный список, двусвязный список) не годится — а хорошо ложиться только… вот это…
GCU
17.12.2019 12:46Т.е. при условиях, когда «двусвязный список» в основном последовательный и очень похож на массив и при некоторых операциях «в одну сторону ходить, не глядя на значение» (для которых в массиве вообще прямая адресация) это будет в три раза (но возможно больше, значение может занимать больше указателя) эффективнее.
P.S. Всё равно не покидает ощущение лёгкой высанонасти :)
khim
17.12.2019 13:42Т.е. при условиях, когда «двусвязный список» в основном последовательный и очень похож на массив
Он по-построению таким будет: дырки при добавлении/удалении элементов уничтожаются…

pvl_1
17.12.2019 11:41Вообще говоря, профита может и не быть, а может быть и деградация. Это сильно зависит от того, как мы эту структуру данных используем. Поэтому к оптимизации AoS->SoA нужно подходить с осторожностью.
Почему оная оптимизация вообще может сработать на утрированном примере: допустим, у нас есть массив структур с 8 4-байтовыми полями, а в некоем цикле мы обращаемся к 3-му полю каждого элемента массива в цикле, причём итерируемся по индексу элемента массива. Допустим, размер кэш-линии L1 у нас 64 байта. Тогда мы можем загружать в кэш-линию по 2 элемента массива, из которых реально в данном конкретном цикле будем трогать 2 4-байтовых поля. Итог: каждые 2 итерации получаем промах кэша L1. После преобразования (именно в SoA, хотя обычно делают несколько AoS с элементами меньшего размера и связями между структурами, чтобы нормально обрабатывать обращения к структурам по указателю) получим промах кэша L1 на каждые 16 итераций — в 8 раз реже. Профит!
А если мы в другом цикле трогаем все поля структуры в течение итерации? Тогда до преобразования был 1 кэш-промах на 2 итерации. После преобразования у нас получится, что все поля лежат в разных кэш-линиях (если нам повезло обойтись без коллизий, но такие коллизии — всё же редкость), что даёт по 1 кэш-промаху на 16 итераций в каждой кэш-линии — 8 кэш-промахов на 16 итераций. Никакого профита, если нам повезло. А если не повезло, то вообще деградацию получили.
Ну и пример с деградацией, подобный Вашему: при случайном доступе, как обычно делается в списках, у нас вместо одного кэш-промаха на всю нашу структуру по 1 промаху на каждое поле, которое трогаем.
Как следствие всего вышесказанного, для проведения оптимизации AoS->SoA крайне желательно исследовать код на такие сценарии использования.
GCU
17.12.2019 12:58Выигрыш для последовательной обработки массивов понятен, благодарю.
Но «двусвязный список» по логике не последователен.

nshalimov Автор
17.12.2019 17:30Тут вам уже немного наотвечали. Я думаю, что стоит посвятить этому отдельный пост в будущем.

aamonster
16.12.2019 14:36+4Сложно как-то. Можно же просто в объекте списка хранить флаг — прямой список или развёрнутый. Инверсия флага – O(1).
А на собеседованиях задачка вроде про односвязный список всегда ставилась...
Jogger
16.12.2019 14:37А разве у двусвязного списка обязательно хранение ссылки на последний элемент? Мне казалось что нет, и тогда в случае если ссылка не хранится — приведенный трюк не сработает.
Но идея хороша.

Deranged
16.12.2019 15:22+4Не пойму. Это статья троллинг? Как предусмотрительно вы не стали писать remove.
У вас получился вектор, ухудшенный в 3 раза. Основное назначение списка — быстрая вставка в середину ценой памяти и скорости итерации. А реверс, как написали выше, решается элементарно std::reverse_iterator.
P.S. Не знаю как у других, но на моей практике в 99.9% всех случаев, когда нужен линейный контейнер, лучше всего подходит вектор, т.к. львиная доля операций с ним — операции чтения данных. Бывает, конечно, что приходится и удалять из середины, но я обычно борюсь
с этим поддержкой «дырок», параллельным вектором индексов и т.д. уловками, когда это возможно.
stan_volodarsky
16.12.2019 18:17Элементы в трёх списках не обязаны быть записаны последовательно. Для добавления нового элемента вы помещаете его в конец списков и ссылками вставляете в нужное место. Для удаления элемента вы убираете его, образуется дырка. В дырку перемещается последний элемент. Ссылки обновляются соответственно.
Все операции за O(1), правда, амортизированный. Надо перевыделять массивы иногда. На деках будет лучше.
Deranged
16.12.2019 19:46Т.е. это для того, что бы отсортировать коллекцию «на лету»? Вы добавили штуку под названием карта индексов (index map). Это по сути «ленивая» сортировка коллекции. Вы платите вектор индексов и косвенную адресацию, за то, что не вызывали std::sort. Ну в принципе да, если элементы натикивают в список один за другим неторопясь, то решение полезное. А если приходит пачка данных, а потом с ней идет работа, я бы перешел на std::vector/std::array + std::sort. Сортировать конечно же 1 раз после получения пачки данных.
Я юзаю такую структурку при наложении фильтров на список элементов (сообщений в списке сообщений и т.д.). Чем перечитывать блок данных с фильтром, куда проще пройтись по уже прочитанному и сформировать вектор индексов элементов, прошедших фильтр. И работает очень быстро. А еще можно распараллелить.
В общем у вас получился уже не двусвязный список. Это вектор с индексной картой. При этом:
— Можно использовать индексную адресацию. Совершенно нет причин делать интерфейс только последовательного доступа. Вектор-то уже всё равно есть.
— Зачем использовать 2 индексных карты (2я для prev_)? 1 вполне достаточно.
— А как же resize? На практике ситуация с известным максимальным размером списка крайне редка.
— В чем профит объединения 2х векторов индексов в 1 (indirection)?
— next_ и prev_ никогда не переприсваиваются. Зачем хранить их как поля? В виде inline функций будет не медленнее.
Я бы это назвал lazy_vector, или как-то так. Можно было бы добавить метод arrange, который бы раскидывал элементы в правильном порядке и вырубал бы косвенную адресацию.
stan_volodarsky
16.12.2019 20:10Индексная адресация не позволяет убрать элемент из середины контейнера за 0(1). Все индексы после удаляемого надо будет сдвинуть. Обратное надо будет делать при вставке элемента в середину.
Контейнер из статьи позволяет удаление и вставку за константу.
Про resize я упомянул, когда сказал что константа амортизированная.
Next и prev изменяются при вставке и удалении.
Несмотря на использование массивов, этот контейнер проявляет все свойства двусвязного списка. Амортизированность немного портит дело, но его можно поправить перейдя с векторов на деки.
В итоге мы имеем контейнер, который работает как двусвязный список и ещё память экономит.

nshalimov Автор
17.12.2019 00:21Не стал писать remove потому, что это не имело отнишения к делу. Специально для вас быстренько накидал. Без дырок. Можно лучше, но быстренько вот так:
void remove(node n) { auto prev = prev_[n.index]; auto next = next_[n.index]; if (prev == INVALID_INDEX) first_ = next; else next_[prev] = next; if (next == INVALID_INDEX) last_ = prev; else prev_[next] = prev; if (--length_ == n.index) return; prev = prev_[length_]; next = next_[length_]; data_[n.index] = data_[length_]; prev_[n.index] = prev; next_[n.index] = next; if (prev == INVALID_INDEX) first_ = n.index; else next_[prev] = n.index; if (next == INVALID_INDEX) last_ = n.index; else prev_[next] = n.index; }

S-e-n
16.12.2019 15:25+2Строго говоря, может это и не двусвязный список. Но решение имееет применение в определённых случаях. Автору спасибо.

CryptoPirate
16.12.2019 17:56Можно вставить и удалить узлы (из/в середину/начало/конец) за константное время.
В начало — да. В конец — да. В середину — только если у вас туда уже есть указатель, если у вас есть просто сам объект, то до серидины нужно ещё «доползти».

chapuza
16.12.2019 20:17+2Скорее всего, вы найдёте её реализацию в стандартной библиотеке любого другого языка.
А ничё, что ни в одном функциональном (иммутабельном) языке двусвязный список построить просто физически невозможно? Ни в стандартной библиотеке, ни в нестандартной.

0xd34df00d
17.12.2019 22:37+1Вы просто не любите узлы:
import qualified Data.IntMap as IM data DList a = Nil | DCons a (DList a) (DList a) deriving (Eq, Show) toDList :: [a] -> DList a toDList [] = Nil toDList lst = knots IM.! 0 where knots = IM.fromList [ (idx, DCons elt (leftOf idx) (rightOf idx)) | (idx, elt) <- zip [0..] lst ] len = length lst leftOf 0 = Nil leftOf k = knots IM.! (k - 1) rightOf k | k == len - 1 = Nil | otherwise = knots IM.! (k + 1)Примерimport qualified Data.IntMap as IM import Data.Maybe data DList a = Nil | DCons a (DList a) (DList a) deriving (Eq, Show) toDList :: [a] -> DList a toDList [] = Nil toDList lst = knots IM.! 0 where knots = IM.fromList [ (idx, DCons elt (leftOf idx) (rightOf idx)) | (idx, elt) <- zip [0..] lst ] len = length lst leftOf 0 = Nil leftOf k = knots IM.! (k - 1) rightOf k | k == len - 1 = Nil | otherwise = knots IM.! (k + 1) dlast :: DList a -> Maybe (DList a) dlast Nil = Nothing dlast elt@(DCons _ _ Nil) = Just elt dlast (DCons _ _ r) = dlast r collectRight :: DList a -> [a] collectRight Nil = [] collectRight (DCons elt _ r) = elt : collectRight r collectLeft :: DList a -> [a] collectLeft Nil = [] collectLeft (DCons elt l _) = elt : collectLeft l main :: IO () main = do let dlist = toDList [1..10] print $ collectRight dlist print $ collectLeft $ fromJust $ dlast dlistвыводит
[1,2,3,4,5,6,7,8,9,10] [10,9,8,7,6,5,4,3,2,1]как и ожидалось.
И никакой грязи.

malishich
16.12.2019 22:16+2Положим есть список и его last элемент:
struct node { int data; node* next; node* prev; };
Для разворота за O(1) пишемstruct rnode { int data; node* prev; node* next; };
И код:node * realLast = somePointer; rnode * reverseFirst = (rnode*)realLast; // O(1) , кээп!
;-)
nshalimov Автор
17.12.2019 00:51Это, конечно, элегантно) Только, во-первых, у вас опечатка
struct rnode { int data; rnode* prev; rnode* next; };Во вторых, вам придётся писать по две реализации любой функции, которая принимает ваш список.
Но попытка хороша)
chapuza
17.12.2019 08:51-1по две реализации любой функции, которая принимает ваш список
Зачем? При развороте за
O(1)можно хоть в коллере, хоть в колли хоть пять раз развернуть входной параметр куда надо.

twaikyont
17.12.2019 12:27Мне понравилось как реализован двусвязный список в libwayland. Если кратко — обычные prev/next, но у первого элемента prev указывает на последний элемент, у последнего next указывает на первый элемент. Что-то вроде кольцевого списка.
Описание структуры, связанный код.
mayorovp
17.12.2019 12:55Это называется "кольцевой двусвязный список с заголовком". Точнее, то что вы описали называется "кольцевой двусвязный список без заголовка", но libwayland всё-таки использует отдельный заголовок.

nickolaym
17.12.2019 18:53+1Ладно. Раз уж тут пошли читерские решения, то давайте я покажу, как это делается на честных списках, а не на массивах-с-индексами.
(писал с листа, если где накосячил — извиняйте, компилировать и тестировать было влом)
struct list { struct node { node* siblings[2]; // обезличиваю prev/next для МАГИИ SOME data; }; node terminator; // для простоты алгоритмов, список с заглушкой bool direction; // МАГИЯ bool back() const { return !direction; } bool forth() const { return direction; } list() : terminator{{&terminator, &terminator}}, direction{true} // не имеет значения, на самом деле {} void reverse() { direction = !direction; // МАГИЯ } struct iterator { list* domain; node* item; bool operator==(const iterator& another) const { assert(domain == another.domain); return item == another.item; } void assert_dereferenceable() const { assert_valid(); assert(domain); assert(item); assert(item != &domain.terminator); } SOME& operator*() const { assert_dereferenceable(); return item->data; } iterator& operator++() { assert_dereferenceable(); item = item->siblings[domain->forth()]; // МАГИЯ return *this; } iterator& operator--() { assert_dereferenceable(); item = item->siblings[domain->back()]; // МАГИЯ return *this; } }; iterator begin() { return iterator {this, terminator.siblings[forth()]}; // МАГИЯ } iterator end() { return iterator {this, &terminator}; } // вставка нового элемента в точку перед итератором iterator insert(const iterator& it, SOME data) { node* new_node = new node{{nullptr, nullptr}, data}; // МАГИЯ node* prev_node = it->node.siblings[back()]; node* next_node = it->node; new_node->siblings[back()] = prev_node; new_node->siblings[forth()] = next_node; prev_node->siblings[forth()] = next_node->siblings[back()] = new_node; return iterator{this, new_node}; } };
niktomsk
24.12.2019 11:43А теперь соединить надо два списка с разным направлением. Можно это за O(1) сделать?
А вот задача переворота двухсвязоного списка скорее всего нужна перед соединением этих списков. Иначе зачем его разворачивать.
Автор молодец спасибо дал возможность немного подумать.
nickolaym
26.12.2019 03:12Можно подумать в сторону склеивания cons- и snoc-списков.
Список — это вырожденное дерево. Но если мы рассмотрим, например, невырожденное дерево, в котором существует возможность обхода за O(1), то можем притвориться, что это и есть список.
Я сейчас только направления накидаю.1) Это, конечно же, функциональные структуры Криса Окасаки.
Там даже не деревья, а какие-то леса могут появиться.
Дешёвые копирования-с-изменением иммутабельных деревьев, вот это вот всё.2) Обобщение биди-текста с управляющими скобками.
Вот чисто для дальнейшей работы, концепция.
Пусть каждый узел содержит флажок, как интерпретировать указатели на его соседей.
Но не влево-вправо / вправо-влево (зачем нам такой флажок? обменяли значения, и всё),
а "как у предыдущего узла" / "наоборот".
Генеральное направление задаётся в шапке списка. Дальше, для обхода вправо, идём по первому указателю и дальше ксорим флажки.
Разворот списка — инверсия флажка в шапке.
Склеивание списков — у одного из списков может потребоваться инверсия флажка головного элемента.
Вот время жизни итераторов, конечно, пострадает… Но нужны ли живые итераторы при инверсии/склеивании? Или же мы должны в этот момент оперировать списками только как единым целым?


Max173
Я один ржал на работе увидев картинку к посту?
Druu
deleted
softaria
да