Главная
Магия тензорной алгебры: Часть 18 — Математическое моделирование эффекта Джанибекова

Магия тензорной алгебры: Часть 18 — Математическое моделирование эффекта Джанибекова +25

08.08.2015 13:02

maisvendoo 14 9446 Источник

Содержание

Введение

Прошлая статья должна была быть о численном моделировании эффекта Джанибекова, но мне внезапно пришла в голову мысль, что этот эффект можно исследовать качественно, пусть и довольно приближенным первым методом Ляпунова. Однако, численное моделирование тоже весьма интересный вопрос, тем более лежащий в плоскости моих исследовательских задач. Поэтому, сегодня мы

Окончательно определимся с тем, как использовать параметры Родрига-Гамильтона для описание ориентации тела в пространстве
Рассмотрим формы представления уравнений движения свободного тела: покажем как тензорные уравнения можно превратить в матричные и компонентные.
Выполним моделирование движения свободного твердого тела при различных соотношениях между главными моментами инерции и покажем, как проявляет себя эффект Джанибекова.

1. Дифференциальные уравнения свободного движения в тензорной форме

Мы уже не раз рассматривали эти уравнения в векторном виде

$\begin{align*} &m \, \vec a_{c} = \sum \vec F_k^{\,e} \&\mathbf I_c \, \vec\epsilon + \vec\omega \times \left(\mathbf I_c \, \vec\omega \right) = \sum \vec M_{c}(\vec F_k^{\,e}) \end{align*}$

Векторная форма записи удобна для общего анализа характера зависимостей, она привычна и в ней видно, что означает конкретное слагаемое. Однако, для дальнейшего преобразования уравнений в форму, удобную для моделирования, перейдем к тензорной записи

$\begin{align*} &m \, \left(\ddot x^{\,i} + \Gamma_{\,kl}^{\,i} \, \dot x^{\,k} \, \dot x^{\,l} \right) = X^{\,i} \&I_{\,j}^{\,i} \, \dot\omega^{j} + \varepsilon^{\,ijk} \, \omega_{\,j} \, g_{\,kl} \, I_{\,p}^{\,l} \, \omega^{\,p} = M^{i} \end{align*}$

где $x^{\,i}$ — контравариантные координаты центра масс тела; $X^{\,i}$ — контравариантные компоненты главного вектора внешних сил, приложенных к телу; $M^{\,i}$ — контравариантные компоненты главного момента внешних сил, приложенных к телу.

Система уравнений (2) уже является замкнутой, интегрируя её можно получить закон движения центра масс и зависимость угловой скорости тела от времени. Но, нас ещё будет интересовать ориентация тела, поэтому дополним данную систему уравнений

$2 \, \varepsilon^{\,ijk} \, \lambda_{\,j} \, \dot\lambda_{\,k} + 2 \, \lambda_0 \, \dot\lambda^{\,i} - 2 \, \lambda^{\,i} \, \dot\lambda_0 = \omega^{\,i}$

Уравнение (3) есть ничто иное как представление компонент угловой скорости через параметры ориентации Родрига-Гамильтона. Это выражение мы уже получали в предыдущих статьях. Теперь мы будем рассматривать его как дифференциальное уравнение, связывающее параметры ориентации с компонентами угловой скорости.

Однако, параметры Родрига-Гамильтона являются избыточными — их четыре, а для описания ориентации тела в пространстве достаточно трех координат. И число неизвестных в системе (2), (3) превышает число уравнений на единицу. Значит нам придется дополнить уравнения (2) и (3) уравнением связи между параметрами ориентации. В статье о параметрах Родрига-Гамильтона мы показали, что поворот тела удобно описывать единичным кватернионом, что есть

$\lambda_0^2 + \lambda_1^2 + \lambda_2^2 + \lambda_3^2 = 1$

или, в тензорном виде

$\lambda_0^2 + \lambda_{\,i} \, \lambda^{\,i} = 1$

Продифференцируем (4) по времени

$2\, \lambda_0 \, \dot\lambda_0 + \dot\lambda_{\,i} \, \lambda^{\,i} + \lambda_{\,i} \, \dot\lambda^{\,i} = 0$

С учетом коммутативности скалярного произведения полагаем $\dot\lambda_{\,i} \, \lambda^{\,i} = \lambda_{\,i} \, \dot\lambda^{\,i}$ , тогда

$\lambda_0 \, \dot\lambda_0 + \lambda_{\,i} \, \dot\lambda^{\,i} = 0$

и есть искомое уравнение связи. Полная система уравнений движения свободного твердого тела в тензорной форме будет иметь вид

$\begin{align*} &\dot x^{\,i} - v^{\,i} = 0 \&m \, \left(\dot v^{\,i} + \Gamma_{\,kl}^{\,i} \, v^{\,k} \, v^{\,l} \right) = X^{\,i} \&2 \, \varepsilon^{\,ijk} \, \lambda_{\,j} \, \dot\lambda_{\,k} + 2 \, \lambda_0 \, \dot\lambda^{\,i} - 2 \, \lambda^{\,i} \, \dot\lambda_0 - \omega^{\,i} = 0 \&\lambda_0 \, \dot\lambda_0 + \lambda_{\,i} \, \dot\lambda^{\,i} = 0 \&I_{\,j}^{\,i} \, \dot\omega^{j} + \varepsilon^{\,ijk} \, \omega_{\,j} \, g_{\,kl} \, I_{\,p}^{\,l} \, \omega^{\,p} = M^{i} \end{align*}$

Довольно страшновато — (6) содержит 13 нелинейных дифференциальных уравнений первого порядка с 13 неизвестными величинами. Страшно выглядит из-за общей тензорной записи, но при переходе к конкретным координатам, в нашем случае декартовым, система (6) значительно упростится.

2. Матричная форма дифференциальных уравнений движения твердого тела в декартовом базисе

Введем вектор-столбец фазовых координат тела

$\mathbf y = \begin{bmatrix} \mathbf x^T && \mathbf q^T && \mathbf v^T && \mathbf \omega^T \end{bmatrix}^T$

где $\mathbf x = \begin{bmatrix} x_c && y_c && z_c \end{bmatrix}^T$ и $\mathbf v = \begin{bmatrix} v_{cx} && v_{cy} && v_{cz} \end{bmatrix}^T$ — положение и скорость центра масс тела; $\mathbf q = \begin{bmatrix} \lambda_0 && \lambda_1 && \lambda_2 && \lambda_3 \end{bmatrix}^T$ и $\mathbf \omega = \begin{bmatrix} \omega_x && \omega_y && \omega_z \end{bmatrix}^T$ — ориентация и угловая скорость тела.

В декартовом базисе метрический тензор представлен единичной матрицей а символы Кристоффеля равны нулю, поэтому система уравнений (6) в матричной форме запишется так

$\begin{align*} &\mathbf{\dot x} - \mathbf v = \mathbf 0 \& 2\, \mathbf B \, \mathbf{\dot q} - \mathbf D \, \mathbf \omega = \mathbf 0 \\ &m \mathbf{\dot v} = \mathbf X \&\mathbf I_c \, \mathbf{\dot\omega} + \mathbf \Omega \, \mathbf I_c \, \mathbf \omega = \mathbf M_c \end{align*}$

где введены матрицы

$\mathbf B = \begin{bmatrix} \lambda_0 && \lambda_1 && \lambda_2 && \lambda_3 \-\lambda_1 && \lambda_0 && -\lambda_3 && \lambda_2 \-\lambda_2 && \lambda_3 && \lambda_0 && -\lambda_1 \-\lambda_3 && -\lambda_2 && \lambda_1 && \lambda_0 \\end{bmatrix}, \quad \mathbf D = \begin{bmatrix} \mathbf 0^T \\mathbf E \end{bmatrix}, \quad \mathbf \Omega = \begin{bmatrix} 0 && -\omega_z && \omega_y \\omega_z && 0 && -\omega_x \-\omega_y && \omega_z && 0 \end{bmatrix}$

Разрешая систему (7) относительно первых производных, получаем

$\begin{align*} &\mathbf{\dot x} = \mathbf v \& \mathbf{\dot q} = \frac{1}{2} \, \mathbf B^{-1} \, \mathbf D \, \mathbf \omega \\ &\mathbf{\dot v} = \frac{1}{m} \, \mathbf X \&\mathbf{\dot\omega} = \mathbf I_c^{-1} \, \left(\mathbf M_c - \mathbf \Omega \, \mathbf I_c \, \mathbf \omega \right) \end{align*}$

систему уравнений движения в форме Коши.

3. Моделирование эффекта Джанибекова

В отсутствие внешних силовых факторов правая часть системы (8) равна нулю, и уравнение движения центра масс интегрируется легко, с учетом начальных условий

$\mathbf x(t) = \mathbf x_0 + \mathbf v_0 \, t$

Вращение гайки описывается системой семи уравнений первого порядка, которые получаем из (8), вводя безразмерные моменты инерции $i_y = \frac{I_y}{I_x}$ и $i_z = \frac{I_z}{I_x}$

$\begin{align*} &\dot\lambda_0 = -\frac{1}{2} \, \left( \lambda_1 \, \omega_x + \lambda_2 \, \omega_y + \lambda_3 \, \omega_z \right) \&\dot\lambda_1 = \frac{1}{2} \, \left( \lambda_0 \, \omega_x + \lambda_3 \, \omega_y - \lambda_2 \, \omega_z \right) \\ &\dot\lambda_2 = -\frac{1}{2} \, \left( \lambda_3 \, \omega_x - \lambda_0 \, \omega_y - \lambda_1 \, \omega_z \right) \\ &\dot\lambda_3 = \frac{1}{2} \, \left( \lambda_2 \, \omega_x - \lambda_1 \, \omega_y + \lambda_0 \, \omega_z \right) \&\dot\omega_x = \left(i_y - i_z) \, \omega_y \, \omega_z \&\dot\omega_y = \frac{i_z - 1}{i_y} \, \omega_x \, \omega_z \&\dot\omega_z = \frac{1 - i_y}{i_z} \, \omega_x \, \omega_y \end{align*}$

Для численного интегрирования системы (9) зададим начальные условия

$\begin{align*} &\lambda_0(0) = 1, \quad \lambda_1(0) = \lambda_2(0) = \lambda_3(0) = 0 \&\omega_x(0) = \omega_0, \quad \omega_y(0) = \Delta\omega_y, \quad \omega_z(0) = 0 \end{align*}$

где $\omega_0$ — угловая скорость гайки после схода с резьбы; $\Delta\omega_y$ — начальное возмущение угловой скорости

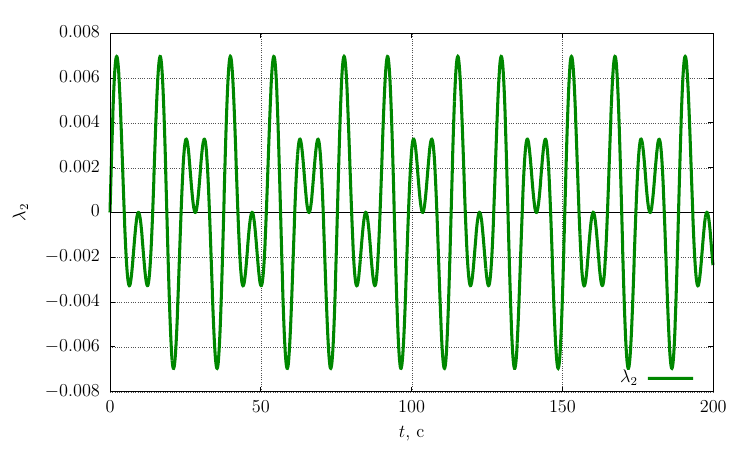
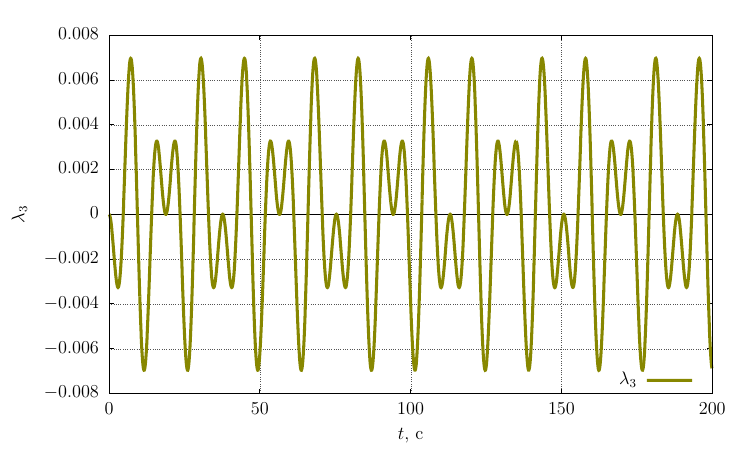
При значениях параметров $i_y = 2.0, \, i_z = 0.5, \, \omega_0 = 1.0$ , рад/с, $\Delta\omega_y = 1 \cdot 10^{-10}$ , рад/с, движение гайки происходит следующим образом

Параметры ориентации Родрига-Гамильтона

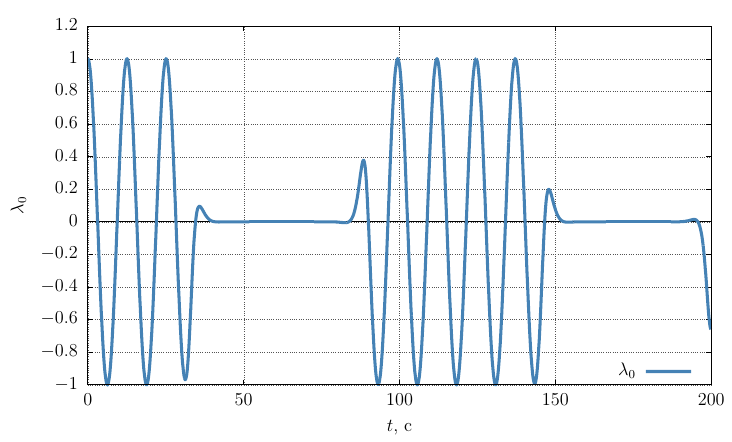
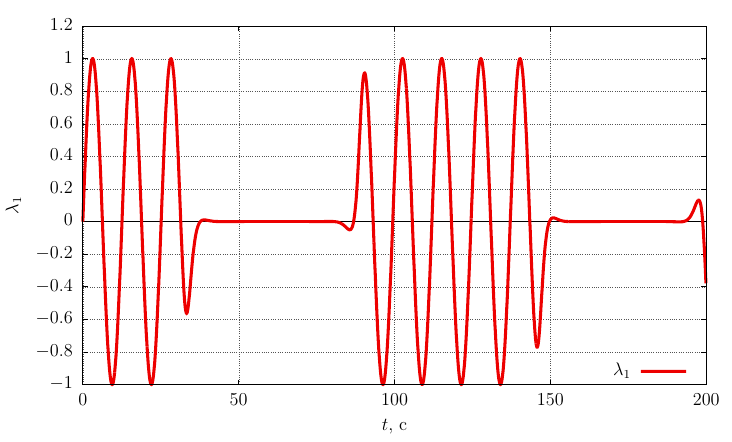
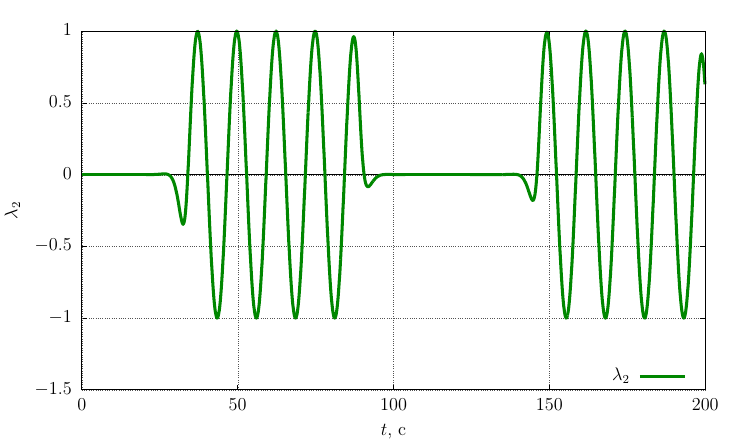
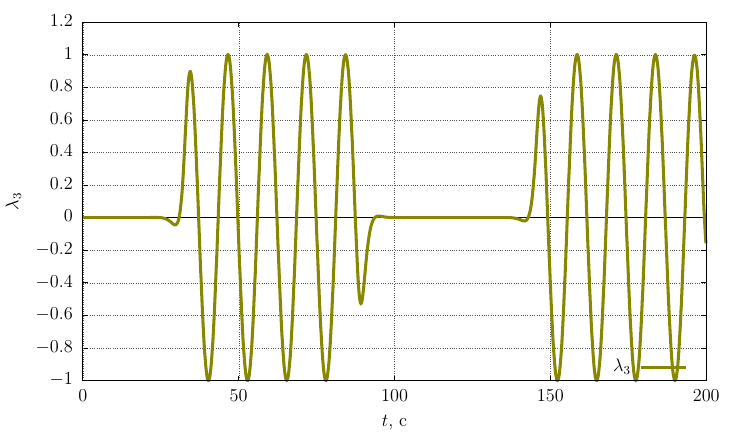
Проекции угловой скорости на собственные оси

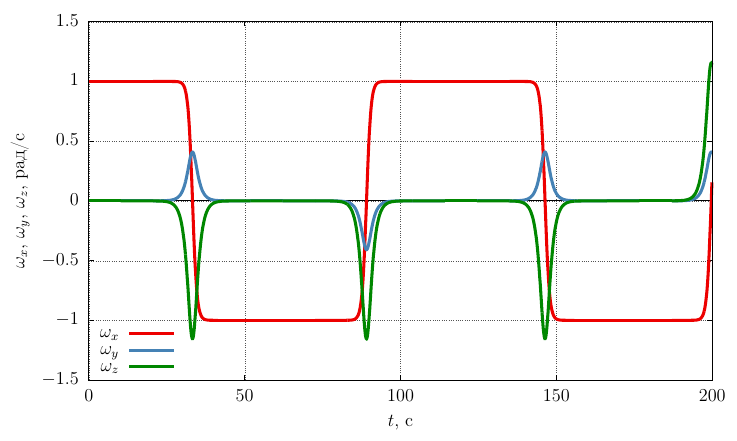
Из графиков видно, что при $I_y > I_x > I_z$ , весьма незначительное возмущение вектора угловой скорости приводит к периодическому лавинообразному изменению ориентации гайки в пространстве.

Сравним полученный результат с движением тела, закрученным вокруг оси с максимальным моментом инерции, то есть положим $I_x > I_y = I_z$ , задав следующие значения параметров $i_y = 0.5, \, i_z = 0.5, \, \omega_0 = 1.0$ , рад/с, $\Delta\omega_y = 1 \cdot 10^{-2}$ , рад/с

Параметры ориентации Родрига-Гамильтона

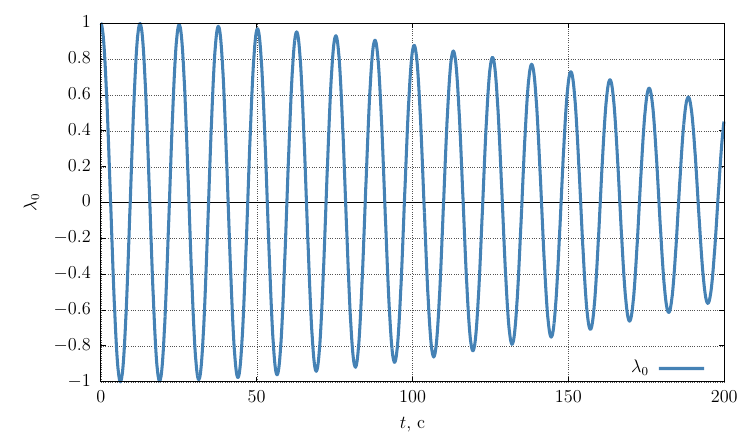
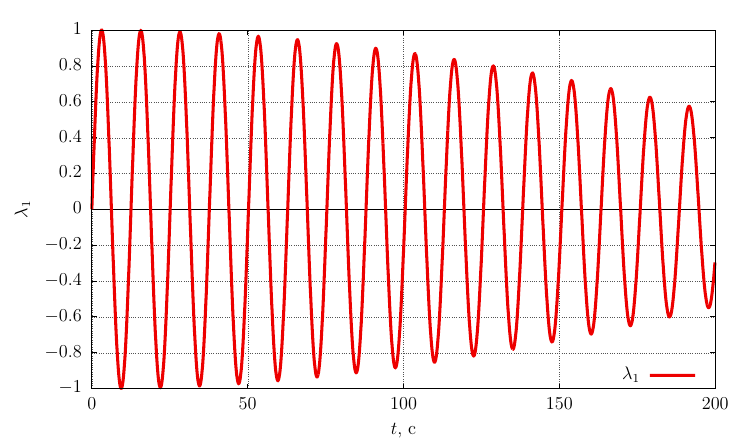
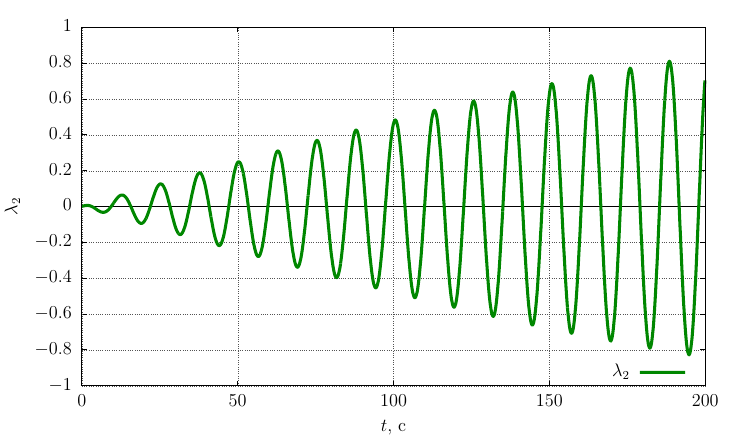
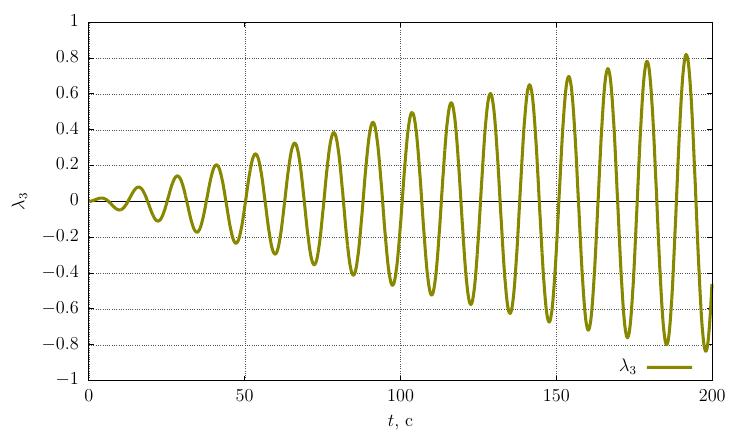
Проекции угловой скорости на собственные оси

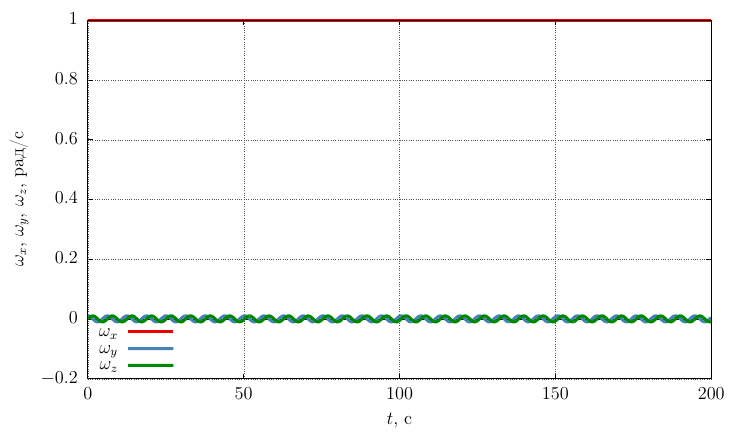
Видно, что при достаточно значительном возмущении угловой скорости движение остается устойчивым вращением вокруг оси $x$ с небольшой прецессией.

Похожая картина наблюдается для тела, закручиваемого вокруг оси с минимальным моментом инерции ( $I_x < I_y = I_z$ ) $i_y = 1.5, \, i_z = 1.5, \, \omega_0 = 1.0$ , рад/с, $\Delta\omega_y = 1 \cdot 10^{-2}$ , рад/с

Параметры ориентации Родрига-Гамильтона

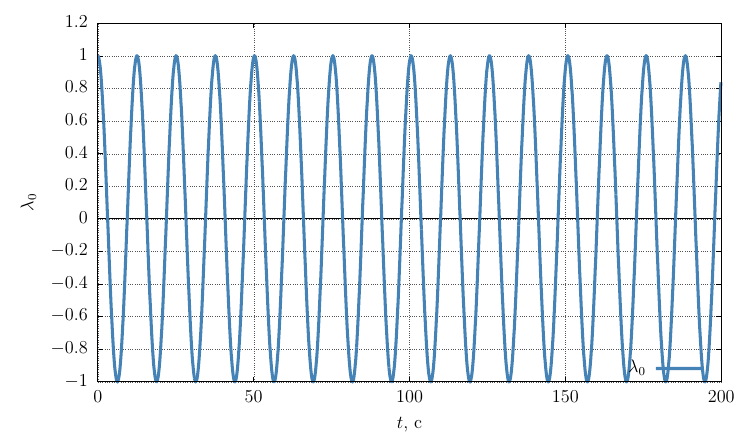
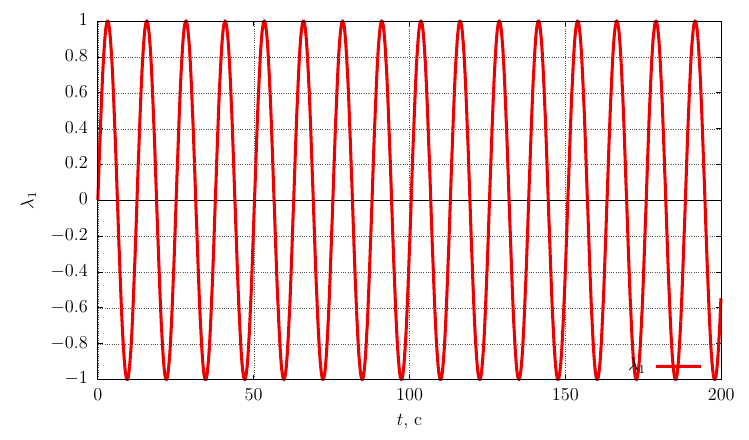
Проекции угловой скорости на собственные оси

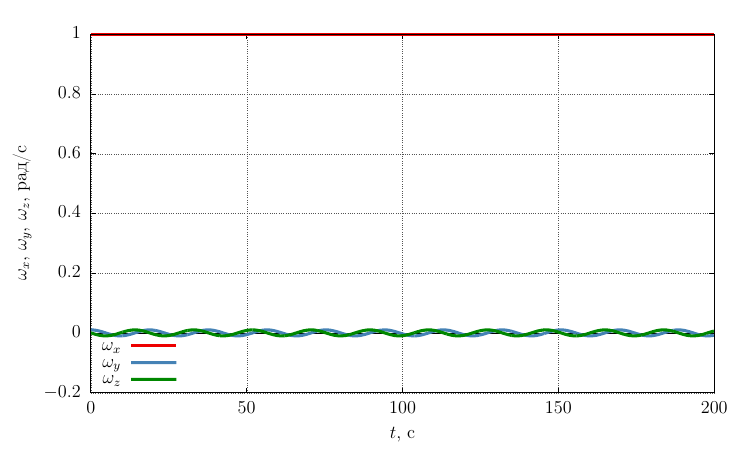
Частота прецессии существенно меньше, чем при закрутке вокруг оси с максимальным моментом инерции, что логично, так как колебания происходят вокруг оси с большим моментом инерции, чем в случае $I_x > I_y = I_z$ .

Заключение

Все расчеты выполнены автором в СКА Maple 18. Графики построены из лога расчета связкой Kile + LaTeX + gnuplot.

Хотелось бы ещё сделать анимацию, однако опыт автора в этом вопросе крайне мал. Поэтому хотел бы задать вопрос читателям — существует ли ПО (для Linux/Windows), с помощью которого имея набор значений параметров кватерниона ориентации в зависимости от времени сделать анимационный ролик, иллюстрирующий движение тела? Подозреваю, что подобное можно провернуть с Blender 3D, но не уверен.

А пока что, благодарю за внимание!

Upd:

Благодарности

Однако, я совершенно забыл написать о том, что данная статья (и предыдущая) подготовлена с использованием веб-приложения Markdown & LaTeX Editor, разработанный пользователем parpalak. Данная система позволяет набирать тексты статей в Makdown и LaTeX и генерирует код, пригодный для непосредственной вставки в хабра-редактор. Признателен автору за участие в тестировании продукта. С его разрешения, рекомендую данную систему к использованию при подготовке математизированных текстов статей

Продолжение следует…

Комментарии (14)

lamerok
08.08.2015 21:12
#8529721
Unity3D нет? docs.unity3d.com/ScriptReference/Quaternion.Euler.html

parpalak
09.08.2015 19:46
#8530087
Я тут подумал, а можно ли аналитически вычислить время переворачивания гайки (43 сантиметра из предыдущей статьи)?

С первого взгляда кажется, что это время зависит от возмущения $delta omega$ . Если возмущение нулевое, время равно бесконечности. Какая зависимость времени переворачивания от $delta omega$ ?

Было бы интересно с помощью моделирования определить время для нескольких значений возмущений и построить график.
1. maisvendoo
  09.08.2015 20:02
  #8530105
  От возмущения не зависит. Возмущение принимается бесконечно малой величиной, что мы о нем знаем? При численном счете мы, разумеется принимаем конкретные значения, но по сути возмущения лежат в окрестности установившегося режима движения и малы.
  
  А вот от начальной угловой скорости установившегося вращения и от безразмерных моментов инерции i_y и i_z — очень даже зависит. Это можно было конечно показать, и построить графики, но надо существенно модифицировать программу на Maple. Теперь жалею, что не заморочился. Но думаю, когда сделаю 3d-ролик в той же статье приведу и такие графики.
  1. parpalak
    09.08.2015 20:26
    #8530115
    Это вы выбрали возмущение малым, чтобы построить графики. Но ясно, что от величины возмущения будет зависеть, через какие промежутки времени тело переворачивается (у вас сейчас ~55 секунд). Иными словами, красные горизонтальные участки должны быть тем длиннее, чем меньше возмущение:
    
    Если возмущение нулевое, то тело всегда будет вращаться вокруг оси с промежуточным моментом инерции, так как является решением (хоть и неустойчивым) уравнений (9).
    
    maisvendoo
    10.08.2015 03:05
    #8530277
    Нет, возмущение будет именно малым. Если, например сравнимо с , то это уже совершенно другой режим установившегося движения, вопрос о об устойчивости которого следует решать, опять вводя малые возмущения.
    
    Не путайте начальные условия и возмущения. Начальные условия четко определены, возмущения же — продукт действия неучтенных внешних факторов, как-то вязкость воздуха и его движение, микрогравитация, несовершенство резьбы винта, с которого начала движение гайка.
    
    Задать малое возмущение в виде начального условия — самый простой вариант возмутить движение при моделировании, особенно в отсутствие малых силовых факторов, которыми мы пренебрегаем.
    
    Но, повторюсь, задание угловых скоростей по оставшимся осям, так чтобы они были сравнимы с рассматриваемой омегой — означает задать совершенно другой режим движения. Мы его в контексте данной задачи не рассматриваем. Мы рассматриваем вращение гайки вокруг оси x.
    
    Кстати, то движение которое начинается после лавинообразного переворота уже тоже не относится к первоначальному неустойчивому вращению, так как отклонение достигло таких величин, что движение окончательно ушло от первоначального режима. На графике, что Вы привели в комментарии — мы изучаем устойчивость движения от 0 до около 35 секунд. Дальше уже другое движение — система неустойчива
    
    maisvendoo
    10.08.2015 03:17
    #8530279
    Объяснение того, что есть дается в следующей статье-довеске, в разделе посвященном функциям Ляпунова. Четко говорится о том, что функции, определяющие возмущенное движение удовлетворяют условию
    
    где h — достаточно малое число.
    
    maisvendoo
    10.08.2015 03:25
    #8530281
    Ведь можно рассматривать и, например, задачу об устойчивости программного поворота спутника на орбите, когда вектор угловой скорости меняется по некоторому закону . Этот закон будет установившимся режимом, а возмущенное движение будет отличаться от этого режима на некоторую малую величину . И вот вопрос устойчивости как раз и заключается в выяснении того, останутся ли эти отклонения малыми, сойдутся ли к исходной программе движения или увеличатся, перестав быть малыми и испортив программу управления.
    
    Только в этом случае система уравнений возмущенного движения будет не автономной (коэффициенты, зависящие от программы управления будут зависеть явно от времени), система будет нелинейной, но вопросы устойчивости будут рассматриваться всегда в контексте малых отклонений от программы. В этом вся суть теории устойчивости механического движения
    
    maisvendoo
    10.08.2015 03:37
    #8530283
    Кстати, на том графике, что Вы привели в комментарии, по осям отложены не дельты, там отложены проекции угловой скорости. И этот график показывает, что как ни мало начальное отклонение от установившегося режима (!!!), в силу неустойчивости последнего, отклонение разовьется и даст вращение вокруг осей y и z.
    
    Обратите внимание на график, иллюстрирующий устойчивое вращение
    
    Он показывает, что в случае если рассматриваемое движение устойчиво, то отклонения от него не превысят первоначального возмущения. Отклонение здесь выбрано довольно большим, чтобы были видны колебания, но все же в 100 раз меньше угловой скорости основного вращения.
    
    Так что рассматривать период переворотов как функцию дельт омеги не правильно, исходя из самой сути задачи об изучении устойчивости.
    
    parpalak
    10.08.2015 14:31
    #8530885
    Принимаю поправку насчет терминов (возмущения и начальных условий). Но суть моего вопроса от этого не меняется.
    
    Вектор момента импульса обходит траектории на эллипсоиде из интерпретации Мак-Куллага. Мой вопрос в том, какое время занимает этот обход. Время обхода у каждой траектории своё. Очевидно, выбор начальных условий эквивалентен выбору траектории, больше он ни на что не влияет.
    
    Я поэкспериментировал с маплом. У меня получилось, что с уменьшением отклонения оси вращения от оси с промежуточным моментом инерции время обхода растет логарифмически. Из соображений размерности для угловой скорости $\vec{\omega}=(\omega,\delta\omega,0)$ время обхода должно быть таким: $T\sim{1\over \omega}\ln{\omega\over\delta\omega},\ \delta\omega\to 0$ .
    
    Логарифм наверняка можно получить из эллиптических функций, через которые в общем виде выражается решение уравнений для свободного вращения твердого тела.
    
    Кстати, из первоначальной процитированной вами формулировки следует, что расстояние до переворота в 43 сантиметра повторялось от измерения к измерению. Скорее всего это объясняется неточностью изготовления гайки: ось ее вращения не совпадает с осью с промежуточным моментом инерции. Неопределенность начальных условий (то, как гайка болталась при закручивании) была небольшой и влияла меньше, чем несовпадение осей. Иначе гайка пролетала бы различные расстояния и переворачивалась бы в разные стороны.
    
    maisvendoo
    10.08.2015 22:40
    #8531465
    ось ее вращения не совпадает с осью с промежуточным моментом инерции
    
    Почти наверняка не совпадает. Не думаю, что производители гаек для крепления грузов (даже космических) подобным заморачиваются.
    
    Да, однако с величиной начального возмущения интересно поиграться. Вот например просто поменял знаки — получается разная картинка
    
    Движение гайки Джанибекова при различных начальных возмущениях
    
    parpalak
    10.08.2015 23:13
    #8531503
    Не совсем. На первых двух графиках три зеленых «зубца» смотрят в одну сторону, а четвертый в другую. На вторых двух — по два «зубца» смотрят вверх и вниз.
    
    Вообще критические траектории из интерпретации Мак-Куллага делят эллипс на 4 части, в каждой из которых траектории своего типа.
    
    Вот что пишет Журавлев
    
    maisvendoo
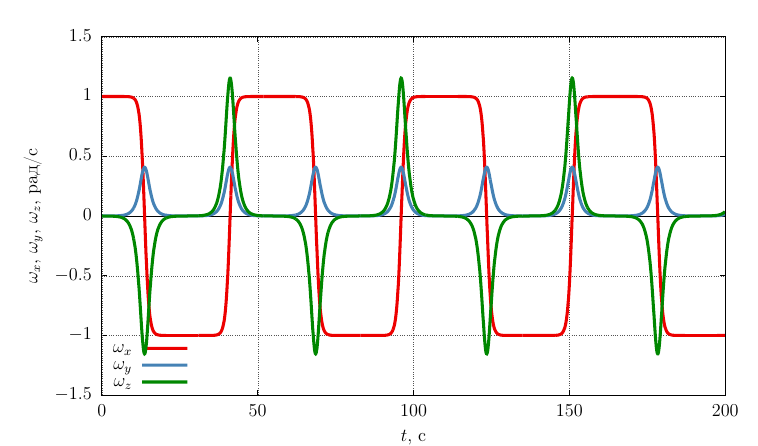
    10.08.2015 22:59
    #8531489
    Ну и еще результаты, для различного значения начального возмущения по оси игрек
    
    Характер движения гайки Джанибекова при различной величине начального возмущения
    $\Delta\omega_y = 0.1, \quad \Delta\omega_z = 0$
    
    $\Delta\omega_y = 0.01, \quad \Delta\omega_z = 0$
    
    $\Delta\omega_y = 0.001, \quad \Delta\omega_z = 0$
    
    $\Delta\omega_y = 0.0001, \quad \Delta\omega_z = 0$
    
    $\Delta\omega_y = 1 \cdot 10^{-5}, \quad \Delta\omega_z = 0$
    
    $\Delta\omega_y = 1 \cdot 10^{-10}, \quad \Delta\omega_z = 0$
    
    $\Delta\omega_y = 1 \cdot 10^{-20}, \quad \Delta\omega_z = 0$
    
    $\Delta\omega_y = 1 \cdot 10^{-30}, \quad \Delta\omega_z = 0$
    
    parpalak
    10.08.2015 23:31
    #8531513
    На последнем графике есть интересный эффект, который я тоже наблюдал в мапле. Первые ~100 секунд ничего не происходит, а потом тело переворачивается с полупериодом ~50 секунд.
    
    Я думаю, что это артефакт численных расчетов, потому что физических причин для такого поведения нет.
    
    Скорее всего в момент переворачивания происходит потеря точности из-за округления, и численный расчет перескакивает к другой траектории на эллипсоиде Мак-Куллага, для которой период меньше. И, наверно, вместо замкнутой линии в ходе моделирования получается незамкнутая спираль.
    
    Мне кажется, что если применить более точный метод численных расчетов, то полупериод на последнем графике будет ~200 секунд. Я больше доверяю времени до переворота, а не периоду «установившегося» движения, потому что оно растет как нужно, логарифмически: $T\sim\ln{1/\delta\omega}$
    
    maisvendoo
    10.08.2015 23:39
    #8531517
    Надо попробовать интегрировать более точным методом. Использовал «умолчальный» метод в настройках dsolve()