Главная
Вульгаризмы в механике: о вредности термина «замедление»

Вульгаризмы в механике: о вредности термина «замедление» +7

23.04.2017 14:45

maisvendoo 67 4600 Источник

Введение

Довольно часто, особенно в обиходе инженерных дисциплин, употребляется понятие «замедление» то есть ускорение, действие которого приводит к уменьшению модуля скорости. При этом такому ускорению приписывается некий отрицательный знак, подчеркивающий этот самый замедляющий эффект.

По моему скромному мнению данное понятие является не только избыточным, но и вредным с методической точки зрения. Оно бросает своего рода мутную вуаль на суть величин, описывающих механическое движение.

На самом деле, чтобы описать то же торможение автомобиля или парашютиста совершенно необязательно приписывать ускорению знак, достаточно понимания, что ускорение есть величина векторная и умения грамотно переходить от операций с векторами к операциям с их проекциями на оси выбранной системы координат.

Статья имеет своей целью развенчать необходимость использования термина «замедление» при решении практических задач механики, и, если читателя не смущает очередная лекция по теормеху, добро пожаловать под кат.

1. Понятие производной от вектора по времени

Рассмотрим вектор $\vec b$ , такой, что

$\vec b = \vec b(t)$

то есть модуль и направление этого вектора зависят от времени. Вычислим изменение изменение этого вектора, произошедшее за промежуток времени $\Delta t$

$\Delta \vec b(t) = \vec b(t + \Delta t) - \vec b(t)$

Теперь, используя тот факт, что для векторов определена операция умножения на число, умножим (1) на величину, обратную приращению времени $\frac{1}{\Delta t}$ . В силу того, что $\Delta t > 0$ мы получим вектор $\frac{1}{\Delta t} \, \Delta \vec b(t)$ , направленный в ту же сторону что и вектор (1) (см. рисунок 1)

Рис. 1. Геометрический смысл производной вектора по времени

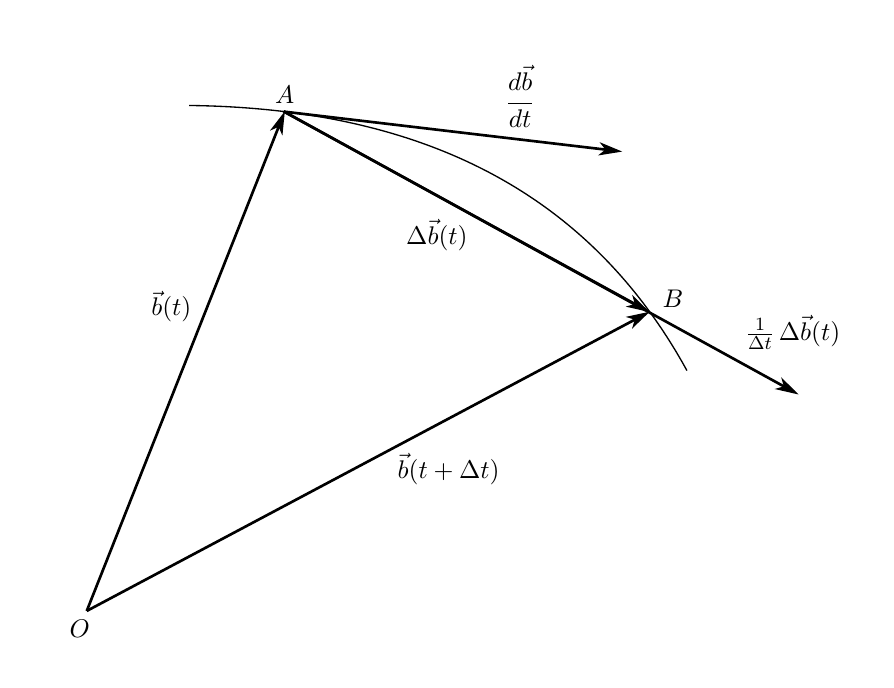
Теперь перейдем к пределу при $\Delta t \to 0$

$\lim_{\Delta t \to 0} \frac{1}{\Delta t} \, \Delta \vec b(t) = \frac{d\vec b}{dt}$

Соотношение (2) есть предел отношения приращения вектор-функции к приращению её аргумента и называется производной вектора по времени. Как видно из наших выкладок производная от вектора по времени также является вектором. Как направлен этот вектор?

Будем рассуждать, глядя на геометрическую интерпретацию на рисунке 1. Вектор $\frac{1}{\Delta t} \, \Delta \vec b(t)$ занимает положение секущей по отношению к траектории, которую описывает конец вектора $\vec b(t)$ за промежуток времени $\Delta t$ . Эта траектория называется годографом вектор-функции $\vec b(t)$ . Секущая пересекает годограф в точках A и B. При стремлении $\Delta t$ к нулю точка A остается неподвижной, а точка B смещается в сторону точки A. В пределе секущая займет положение касательной к годографу в точке A.

То есть, можно ввести следующее определение

Производная от вектора $\vec b(t)$ по времени есть вектор $\frac{d\vec b}{dt}$ , направленный по касательной к годографу вектора $\vec b(t)$

Таким образом, производная от вектора показывает, каким образом меняется как модуль, так и направление вектора. Ни о каком «знаке» производной тут речи не идет в принципе. И не может идти — производная от вектора по времени это так же вектор, а для вектора нет понятия знака.

2. Производная от вектора, постоянного по модулю

Допусти теперь что наш вектор обладает неизменной длиной, то есть

$|\vec b(t)| = b = \text{const}$

а меняется лишь его направление в пространстве. Будет ли у этого вектора отличная от нуля производная? Конечно будет! Умножим вектор скалярно сам на себя

$\vec b \cdot \vec b = |\vec b| \, |\vec b| \, \cos 0 = b^2$

Продифференцируем (3) по времени

$\frac{d}{dt} (\vec b \cdot \vec b) = 2 \, b \, \frac{db}{dt}$

Производная от модуля вектора $\frac{db}{dt}$ равна нулю, ведь модуль не меняется во времени. Тогда, используя правило дифференцирования произведения раскрываем левую часть (4)

$\frac{d\vec b}{dt} \cdot \vec b + \vec b \cdot \frac{d\vec b}{dt} = 0$

используя свойство коммутативности скалярного произведения, получаем

$2 \, \vec b \cdot \frac{d\vec b}{dt} = 0$

или

$\vec b \cdot \frac{d\vec b}{dt} = 0$

То есть, скалярное произведение вектора на собственную производную равно нулю а значит

$\vec b \perp \frac{d\vec b}{dt}$

Таким образом, производная вектора с постоянной длиной не только не равна нулю, а она есть вектор, перпендикулярный исходному. Годографом такого вектора будет окружность с радиусом, равным длине вектора (рисунок 2).

Мы сталкиваемся с такой ситуацией, когда вычисляем ускорение точки, движущейся равномерно по окружности. У неё есть центростремительное ускорение, перпендикулярное вектору скорости.

Производная от вектора будет равна нулю лишь в том случае, если вектор не меняет ни модуль, ни направление.

Рис 2. Вектор с постоянной длиной, его годограф и производная

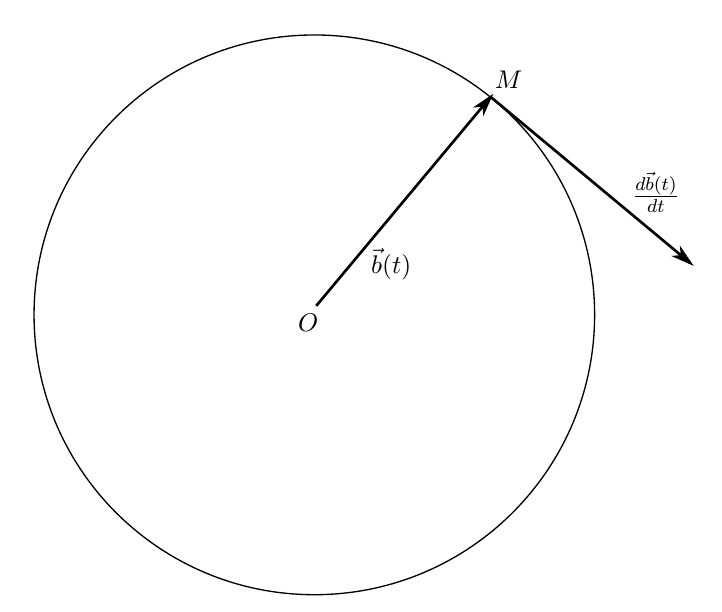
3. Скорость и ускорение

Теперь, исходя из вышеизложенного, дадим определение скорости материальной точки. Пусть положение точки в пространстве характеризуется вектором $\vec r = \vec r(t)$ , называемым радиус-вектором точки (см. рисунок 3). Тогда

Вектором скорости точки $\vec v$ называется первая производная от радиус-вектора точки по времени

$\vec v = \frac{d\vec r}{dt}$

Вектор скорости точки направлен по касательной к её траектории.

Все верно — траектория и есть годограф радиус-вектора, причем выбор начала отсчета O из которого мы выпускаем радиус-вектор роли не играет.

Рис. 3. Векторы скорости и ускорения материальной точки

Аналогичным образом вводится и понятие ускорения

Вектор ускорения точки $\vec a$ есть первая производная от вектора скорости точки по времени

$\vec a = \frac{d\vec v}{dt}$

Вектор ускорения направлен по касательной к годографу вектора скорости.

Геометрическая иллюстрация этих определений показана на рисунке 3. При движении точки по окружности с постоянной по модулю скоростью ускорение направлено точно к центру этой окружности (рисунок 4)

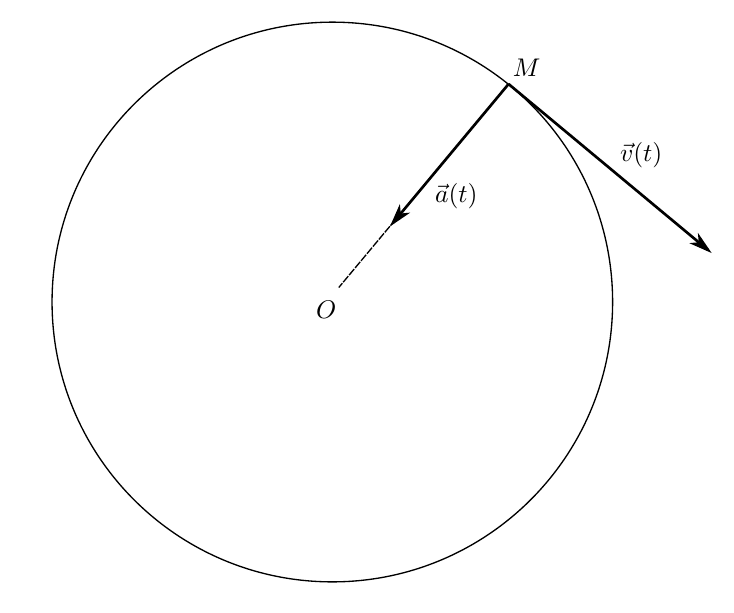
в полном соответствии с определением производной от вектора постоянного по модулю. В этом случае вектор ускорения как раз показывает каким образом меняется направление вектора скорости.

Заключение или откуда всё-таки берется знак

Решая задачу по механике мы неизбежно переходим от векторных уравнений к уравнениям в проекциях на оси выбранной системы координат. И, если вектор ускорения направлен против вектора скорости, то знак его проекции отличается от знака проекции вектора скорости. Причем последняя может быть отрицательной, а проекция ускорения — положительной, все зависит от выбранной системы координат!. Именно в этой ситуации в инженерной практике употребляют термин «замедление».

Однако знак проекции и её именование к механике отношения не имеют, они относятся уже к формальной процедуре вычислений при решении задачи и механического смысла не несут. Так что понятие «замедление» есть результат вольной интерпретации промежуточных результатов вычислений.

Благодарю за проявленное внимание!

Поделиться с друзьями

-->

Комментарии (67)

NaHCO3
23.04.2017 18:05
#10187468
+16
Что-то вы развели панику на пустом месте. Да, ускорение — векторная величина. Что мешает нам ввести классификацию отношений направления вектора ускорения и вектора скорости? Замедление — это когда ускорение направлено в противоположную сторону. Никто же не возражает на классификацию ускорения с делением на тангенциальное и нормальное.
1. maisvendoo
  23.04.2017 18:29
  #10187488
  Что мешает нам ввести классификацию отношений направления вектора ускорения и вектора скорости?
  
  Ничего не мешает нам ввести такую классификацию. Но зачем? Какой смысл во введении избыточных понятий, не несущих физического смысла и являющихся продуктом математических операций, приводящих к решению прикладной задачи.
  
  И как с такой позиции классифицировать скучай движения точки по окружности с постоянной скоростью? Что это — ускорение или замедление?
  
  Есть понятие «вектор ускорения», оно предельно просто и включает в себя все прикладные случаи, несет конкретный физический смысл. Зачем плодить лишние сущности?
  1. michael_vostrikov
    23.04.2017 20:53
    #10187640
    +7
    Какой смысл во введении избыточных понятий, не несущих физического смысла
    Такой же, как и во введении термина "прямой угол" в отличие от "острого" и "тупого". Есть понятие "угол", оно предельно просто и включает в себя все прикладные случаи. Зачем нам отдельно прямой?
    
    И как с такой позиции классифицировать случай движения точки по окружности с постоянной скоростью? Что это — ускорение или замедление?
    Если это нельзя назвать замедлением, то нельзя назвать и ускорением, так как быстрее она не движется.
    
    Вы не делаете различия между физическим явлением, его частными случаями, и их бытовыми названиями.
    Термин "ускорение" произошел как раз из бытового смысла (а не придуман учеными), как изменение скорости в большую сторону, так как это больше всех интересовало. Обратный случай в быту называют замедлением. В науке оно приобрело более широкий смысл как изменение вектора скорости, не только по значению, но и по направлению. Соответственно, осталось только одно название. Хотя логичнее было бы придумать новый термин.
    
    Для частных случаев часто используются свои названия со своей семантикой, это позволяет более емко и точно передавать информацию. Так что нет никакой проблемы в том, что используется слово "замедление" для описания ситуаций, когда значение скорости уменьшается.
    
    maisvendoo
    23.04.2017 21:48
    #10187704
    Вы не делаете различия между физическим явлением, его частными случаями, и их бытовыми названиями. Термин «ускорение» произошел как раз из бытового смысла (а не придуман учеными), как изменение скорости в большую сторону, так как это больше всех интересовало.
    
    «Чойта?» (с) доктор Быков
    
    А если мы посмотрим на формулировку второго закона Ньютона, так сказать в оригинале, из «Начал...»
    
    Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur
    
    что в переводе с латыни означает: «Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует»
    
    Отсюда сразу понятно, что Ньютон постулировал связь между изменением количеством движения (суть скоростью при постоянной массе точки) и силой, используя именно векторный характер величин. Причесав всё это своей теорией «флюксий», то есть производных пришел к классической форме уравнений движений точки известной по сей день.
    
    Так что ввод в науку величин, описывающих механическое движение это сплав эксперимента с хорошей математикой, но никак не плод умозрительного бытового опыта.
    
    И потом, причем тут быт, когда речь идет о методической постановке вопроса, и правильном понимании смысла вводимых величин, облегчающем оперирование ими
    
    maisvendoo
    23.04.2017 22:00
    #10187712
    Оперируя тем же вторым законом и принципом независимости действия сил, можно показать, что ускорение, как продукт действия силы всегда вызывает именно разгон точки в направлении действия силы, поэтому термин «замедление» тут рядом не лежал никак
    
    michael_vostrikov
    24.04.2017 06:04
    #10187928
    Интересно, откуда же он тогда появился и что означает)
    
    michael_vostrikov
    24.04.2017 06:02
    #10187924
    +1
    А если мы посмотрим на формулировку второго закона Ньютона, так сказать в оригинале, из «Начал...»
    Вы серьезно думаете, что до Ньютона никто не замечал изменение скорости?
    
    Так что ввод в науку величин, описывающих механическое движение это сплав эксперимента с хорошей математикой, но никак не плод умозрительного бытового опыта.
    Ввод в науку, естественно, осуществляется учеными. Но само явление сначала отмечалось в быту, а потом его стали изучать ученые. Так происходит почти со всеми наблюдаемыми без специальных приборов явлениями.
    
    И потом, причем тут быт, когда речь идет о методической постановке вопроса, и правильном понимании смысла вводимых величин, облегчающем оперирование ими
    При том, что слово "замедление" используется в быту. Как изначально использовалось и "ускорение".
    
    Есть название для вектора изменения скорости, есть названия для частных случаев, когда модуль скорости увеличивается или уменьшается. Для первого и второго используется одно слово. Вы почему-то считаете, что третье это антоним первого, и что это вызывает у всех путаницу, а второе вообще не рассматриваете. Хотя третье это антоним второго, и оба они частные случаи первого. Обычно смысл понятен из контекста, и путаницы это ни у кого не вызывает.
    
    maisvendoo
    24.04.2017 07:31
    #10187966
    +1
    Вы серьезно думаете, что до Ньютона никто не замечал изменение скорости?
    
    До Ньютона никто не мог связно ответить на вопрос что такое механическое движение и как описать его математически.
    
    Но само явление сначала отмечалось в быту, а потом его стали изучать ученые.
    
    И что, это дает право использовать бытовые понятия в уже сформировавшейся научной дисциплине?
    
    Есть название для вектора изменения скорости, есть названия для частных случаев, когда модуль скорости увеличивается или уменьшается.
    
    Тогда как назвать тот частный случай, когда скорость неизменна по модулю, а точка все равно движется с ускорением? Введем ещё один «вид» ускорения?
    
    Получается по вашему, что методику подачи механики школьнику и студенту следует строить на наборе частных случаев, вводя для одной и той же величины разные названия в зависимости от частного случая? Каким образом тогда соберется общая картина?
    
    Наука наоборот стремится к обобщению фактов, ибо частных случаев бесконечное число. Строить методики на частных случаях, значит приучать людей мыслить однобоко, что годится для решения типовых задач из учебника, но совершенно исключает процедуру создания чего-то нового, в чем цель научного знания и заключается.
    
    michael_vostrikov
    24.04.2017 11:43
    #10188270
    +1
    До Ньютона никто не мог связно ответить на вопрос что такое механическое движение и как описать его математически.
    А причем здесь математическое описание? Увеличение скорости замечали и до этого, и придумали название для этого случая. Значит, название произошло из бытовых наблюдений, а не было придумано учеными.
    
    И что, это дает право использовать бытовые понятия в уже сформировавшейся научной дисциплине?
    Нет, но в самой дисциплине и не используют. Используют при описании ситуаций. Причем как раз потому, что бытовые понятия для всех более знакомы, и это помогает при изучении.
    
    Тогда как назвать тот частный случай, когда скорость неизменна по модулю, а точка все равно движется с ускорением? Введем ещё один «вид» ускорения?
    Можно и ввести, если у вас такие случаи встречаются постоянно. Просто надо понимать, что это не другой термин для другой величины, а название для частного случая существующей.
    
    Получается по вашему, что методику подачи механики школьнику и студенту следует строить на наборе частных случаев, вводя для одной и той же величины разные названия в зависимости от частного случая? Каким образом тогда соберется общая картина?
    Это точно такие же названия одной и той же величины, как и разные названия величины угол (прямой, острый, тупой), цвет (красный, синий, зеленый), изменение расстояния (сближение, удаление), единица измерения объема (литры, кубические метры), а еще как и разные названия многоугольников (квадрат, прямоугольник, ромб), животных (кошки, собаки, обезьяны), и многих других частных случаев общего понятия. А еще есть многозначные слова типа "ключ", которые в разных контекстах означают разные понятия. Вот и у слова "ускорение" 2 разных значения.
    
    У величины "изменение вектора скорости" одно название "ускорение", там нет никаких разных названий. "Замедление" это "изменение вектора скорости, выражающееся в уменьшении ее модуля". С другой стороны, "изменение вектора скорости, выражающееся в увеличении ее модуля" тоже называют "ускорение". Но это не название физической величины, а описание ситуации. Так исторически сложилось. Обычно всем понятно, что имеется в виду, не знаю, почему это вас путает.
    
    Наука наоборот стремится к обобщению фактов, ибо частных случаев бесконечное число. Строить методики на частных случаях, значит приучать людей мыслить однобоко
    А никто и не строит методики на частных случаях. Никто не спорит с тем, что физический термин "ускорение" означает "изменение вектора скорости". Если вы в каком-то учебнике нашли другое мнение, значит это плохой учебник.
    
    maisvendoo
    23.04.2017 22:05
    #10187720
    как изменение скорости в большую сторону
    
    Так что нет никакой проблемы в том, что используется слово «замедление» для описания ситуаций, когда значение скорости уменьшается.
    
    Понятия «больше» и «меньше» к векторным величинам неприменимы. Они применимы к их модулям
    
    michael_vostrikov
    24.04.2017 06:03
    #10187926
    Поэтому я и написал "значение" скорости.
  1. NaHCO3
    24.04.2017 01:32
    #10187854
    +1
    > Ничего не мешает нам ввести такую классификацию. Но зачем?
    
    Потому что в этих случаях система качественно ведёт себя по-разному. И иногда человека не интересует точное числовое решение, ему достаточно качественной характеристики.
    
    Это всё равно, что спрашивать, зачем человек изобрёл понятия «чётное» и «нечётное», когда есть целые числа, несущие полную информацию. Иногда это просто экономит мышление, когда ты получаешь нечётную сдачу при чётной цене и немедленно обнаруживаешь ошибку. Иногда, это позволяет сделать новые наблюдения, которые без этого упрощения, было бы крайней сложно сделать, как например условия решения пятнашек.
    
    maisvendoo
    24.04.2017 07:47
    #10187980
    Потому что в этих случаях система качественно ведёт себя по-разному.
    
    Как это так?
    Возьмем задачу о камне, брошенном с некоторой начальной скоростью у поверхности, не учитывая сопротивление воздуха. Поведение камня совершенно различно и зависит от начального положения, модуля и направления начальной скорости. Траектория зависит от начальных условий. Это качественно разное поведение? А ничего, что во всем наборе возможных траекторий у камня во всех случаях неизменный вектор ускорения? И что дифференциальные уравнения движения во всех случаях одинаковы.
    
    Получается данная система качественно ведет себя одинаково, ибо неизменны законы её поведения.
    
    NaHCO3
    24.04.2017 09:33
    #10188066
    +3
    Машина ускоряется или тормозит. Будет она через секунду ехать быстрее или медленее? Вот вам и качественное различие. Очевидно, что классификация упрощает модель, а значит применима не всегда, а только когда это упрощение уместно. Например для спутника на геостационарной орбите указанная классификация бесполезна и не упрощает работу с информацией. А вот в случае с машиной — упрощает. Ради таких случаев оно и нужно. Точно также проверка чётности может быть полезным приёмом в одних ситуациях, и бесполезным в других.
1. maisvendoo
  23.04.2017 18:32
  #10187496
  Никто же не возражает на классификацию ускорения с делением на тангенциальное и нормальное.
  
  Это не классификация, а форма представления векторного уравнения движения точки в проекциях на естественные оси
1. PapaBubaDiop
  23.04.2017 20:11
  #10187584
  +1
  А если скорость 0? Вы приплыли…
  1. maisvendoo
    23.04.2017 20:14
    #10187588
    Куда я приплыл?
  1. maisvendoo
    23.04.2017 20:18
    #10187598
    А если скорость 0?
    
    В какой момент времени? В любой или в какой-то определенный?
    
    PapaBubaDiop
    23.04.2017 20:40
    #10187624
    Мяч бросаете. в верхней точке — замедление или ускорение?
    
    maisvendoo
    23.04.2017 20:47
    #10187632
    В любой точке траектории мяч движется с ускорением, вектор которого направлен вертикально вниз
    
    PapaBubaDiop
    23.04.2017 21:16
    #10187672
    +1
    Пардон, об этом знает даже мой пятый сын, но мой комментарий был ответом совсем не Вам, а товарищу NaHCO3, чей сомнительный тезис неожиданно заплюсован)

dom1n1k
23.04.2017 18:27
#10187484
+6
Не знаю, никогда не встречал на практике, чтобы слово «замедление» использовали как синоним «отрицательному ускорению». Обычно замедление — это бытовое название самого процесса, а не величины, его характеризующей.
1. maisvendoo
  23.04.2017 19:06
  #10187514
  Далеко ходить не надо, первая же ссылка по запросу «ускорение и замедление» дает потрясающий опус
  http://av-physics.narod.ru/mechanics/acceleration.htm
  есть и ускорение и замедление и «отрицательное ускорение». Заметьте, не проекция ускорения отрицательна там, а именно ускорение
  
  Такие подходы популярны в школьных учебниках, например
  1. arteast
    23.04.2017 23:15
    #10187780
    +1
    Именно так; в учебниках (по крайней мере в том, по которому в свое время учился я) были термины типа "равнозамедленного движения" — с отдельными формулами для них!!! один — и определения типа "если ускорение направлено против направление движения". Потом поверх этого наслаивались задачи в двух измерениях уже в векторах, и картина мира становилась мутной и двоящейся — где там ставить плюсы, где там минусы, и почему?
    
    Zenitchik
    24.04.2017 02:07
    #10187866
    +2
    Странно. Мы одного года рождения, но такие приколы я встречал только в очень старых учебниках — оставшихся от родителей.

amarao
24.04.2017 03:28
#10187896
Последнее время я всё чаще встречаю упоминание слова «замедление» при описании гравитационного воздействия одной массы на другую. Чем больше масса предмета, тем больше замедляются другие объекты, находящиеся рядом с ним.

То же касается и очень быстро летящих объектов. Чем быстрее они летят, тем сильнее замедляются.

sbnur
24.04.2017 07:53
#10187984
+1
Рекомендуется автору использовать в речи выражение — Под действием сил трения тела ускоряются
1. maisvendoo
  24.04.2017 08:48
  #10188002
  +1
  Я же могу порекомендовать Вам воздержаться от неуместного и преждевременного сарказма.
  
  Рассмотрим задачу о качении колеса без проскальзывания, под действием приложенного к нему вращающего момента от двигателя
  
  На рисунке — система сил приложенных к колесу. Сила трения $\vec F_{fr}$ направлена вперед, так как точка контакта колеса и поверхности стремится двигаться назад, из-за того что момент проворачивает колесо. Сила трения покоя не дает проскальзывать точке контакта. Составим дифференциальные уравнения движения
  
  $m \, \ddot x_C = F_{rf}$
  $I_C \ddot \varphi = M - F_{rf} \, R$
  $0 = N - m \, g$
  В силу качения без проскальзывания справедливо уравнение кинематической связи
  
  $v_C = \dot x_C = \omega \, R = \dot \varphi \, R$
  Дифференцируем последнее по времени
  
  $\ddot \varphi = \frac{\ddot x_C}{R}$
  С учетом этого выражения получаем из уравнений движения
  
  $\ddot x_C = \frac{M}{R \, (m + \cfrac{I_C}{R^2})}$
  То есть центр колеса разгоняется, внезапно, по причине наличия силы трения направленной вперед.
  
  Так что сарказм неуместен.
  1. DmitriyDev
    24.04.2017 09:01
    #10188014
    Эм. Шелдон?
  1. sbnur
    24.04.2017 09:27
    #10188048
    не путайте квадратное с зеленым — сила трения может замедлять движение или приводить к удержанию точки тела для создания опоры при движении (то что вы написали)
    Кстати, мы так и ходим- одна нога фиксируется за счет сил трения, другая выносится вперед, создавая ускрояющую силу за счет силы тяжести (именно сила тяжести причина движения)
    
    maisvendoo
    24.04.2017 09:38
    #10188084
    не путайте квадратное с зеленым
    
    Я всего лишь подтверждаю сформулированное Вами
    
    Под действием сил трения тела ускоряются
    
    Тело находится под действием силы трения? Находится. Ускоряется? Ускоряется
    
    Кстати, мы так и ходим- одна нога фиксируется за счет сил трения, другая выносится вперед, создавая ускрояющую силу за счет силы тяжести (именно сила тяжести причина движения)
    
    Причина движения в данном случае не одна конкретная сила, которую Вам удобно выделить. К описанному кинематическому состоянию человеческого тела приводит совокупный эффект от действия системы сил, приложенных к рассмотренной системе
    
    sbnur
    24.04.2017 10:31
    #10188142
    Я вижу вы плохо представляете себе физику качения (но для повышения уровня попробуйте определить распределение скоростей от точки касания до вершины окружности и объяснить для себя)
    
    maisvendoo
    24.04.2017 11:42
    #10188262
    +2
    Вы хотите проэкзаменовать меня что-ли?
    Скорость точки касания всегда равна нулю, скорость самой верхней точки в два раза больше скорости скорости центра колеса. Распределение скоростей точек лежащих на вертикальном диаметре треугольное. Движение колеса плоскопараллельное с мгновенным центром скоростей в точка контакта
    
    Я вижу вы плохо представляете себе физику качения
    
    Укажите на хотя бы одну ошибку в приведенных выше выкладках
    
    sbnur
    24.04.2017 12:53
    #10188400
    Я так и думал — писать формулы не значит понимать — точка касания не движется — поэтому сила трения не есть причина движения (сила трения качения приложена в этой точке), хотя есть условие качения — подумайте об этом
    Но по-моему пытаться вам объяснить бесполезно — поэтому оставайтесь в своем понимании
    
    Zenitchik
    24.04.2017 13:28
    #10188476
    С чего Вы взяли, что Вы понимаете и Ваше понимание правильное? Вы привели словесное описание, которое соотносится с пониманием не лучше, чем формула. То же самое можно описать по другому, различия будут чисто терминологические.
    
    sbnur
    24.04.2017 13:58
    #10188524
    Написано
    "То есть центр колеса разгоняется, внезапно, по причине наличия силы трения направленной вперед."
    Сила трения приложена к точке касания, а не к центру, и скорость ее (точки касания) равна нулю.
    Не сила трения вращает колесо, а поворотный момент, который колесу задан
    Если сила трения такова, что проскальзывания нет, то она приводит к смене точек касания
    Если сила трения мала, то колесо будет проскальзывать (буксовать), то есть вращаться на одном месте
    Причина движения — поворотный момент колеса
    Сила трения определяет не движение колеса, а вид движения — чисто вращательное или поступательное.
    Еще раз повторяю — автор, да и многие, плохо понимают физику качения
    Например, если по шару ударить выше центра, то он будет катиться, а если ниже то скользить.
    PS Когда пишешь формулы, надо их понимать.
    
    maisvendoo
    24.04.2017 14:18
    #10188570
    Сила трения определяет не движение колеса, а вид движения — чисто вращательное или поступательное.
    
    Это не поступательное движение, а плоское
    
    Если сила трения мала, то колесо будет проскальзывать (буксовать), то есть вращаться на одном месте
    
    Правильно, качение, и движение центра колеса ускоренно возможно при достаточной величине силы трения
    
    Причина движения — поворотный момент колеса
    
    Причина движения — совокупное действие всех сил и моментов, а не какой-то одной силы.
    
    Уберите момент при покоящемся колесе — не будет и силы трения, она будет равна нулю.
    Уберите трение — колесо будет проскальзывать с возрастанием угловой скорости.
    
    Ненулевое ускорение центра масс колеса определяется величиной силы трения покоя, величина которой, в свою очередь зависит от величины приложенного к колесу момента
    
    sbnur
    24.04.2017 14:58
    #10188660
    Что значит совокупное действие
    Поворотный момент приводит к возникновению трения в точке касания
    Причина движения — поворотный момент, возникающая сила трения не причина, а следствие
    Далее обсуждение бессмысленно (для меня)
    PS Чему равна сила трения у покоящегося колеса.
    
    maisvendoo
    24.04.2017 14:34
    #10188608
    Например, если по шару ударить выше центра, то он будет катиться, а если ниже то скользить.
    
    Можно уточнить постановку задачи?
    
    sbnur
    24.04.2017 19:56
    #10189112
    да насчет формул по колесу — ответьте по формулам автора на вопрос — чему равна сила трения, если центр колеса движется с постоянной скоростью (или угловая скорость вращения постоянна)
    
    Zenitchik
    24.04.2017 20:30
    #10189170
    
    По условию неподвижности нижней точки и равномерности вращения.
    
    maisvendoo
    24.04.2017 20:40
    #10189180
    В этом случае получается чушь — если Ffr = M/R. что вытекает из второго уравнения, то тогда из первого уравнения вытекает что ускорение центра масс не равно нулю, что нарушает кинематическую связь
    
    Подобной системой уравнений нельзя описать ситуацию качения с постоянной угловой скоростью при M !=0. Для этого требуется ввести в схему трение второго рода — момент трения качения
    
    sbnur
    24.04.2017 21:22
    #10189248
    по уравнению автора при нулевом ускорении сила трения равна нулю
    Вот вам ответ правильны формулы или нет — а объяснять, вижу, вам бесполезно
    
    Zenitchik
    25.04.2017 12:26
    #10190048
    а объяснять, вижу, вам бесполезно
    
    Если, Вы не заметили, мне уже объяснили комментом выше.
    Если Вы не способны объяснить — не пеняйте на оппонента.
    
    sbnur
    25.04.2017 13:19
    #10190172
    видно — jedem das seine
    
    Zenitchik
    25.04.2017 14:28
    #10190316
    Точно. Пойду поработаю. На этот счёт тоже есть немецкая поговорка.
1. NIN
  24.04.2017 20:36
  #10189178
  +2
  То, что тела могут ускоряться под действием сил трения — очевидно.
  Когда вы дергаете за скатерть, лежащую на столе, то предметы, стоящие на скатерти, начинают ускоряться, причём именно из-за трения.
  1. maisvendoo
    24.04.2017 20:40
    #10189182
    Остроумно )
  1. sbnur
    24.04.2017 22:23
    #10189340
    Вы путаете силу трения покоя и силу трения скольжения (или качения) — говорилось про последние
    Сила трения покоя — это сила противоложная приложенной силе и равная ей по величине пока не превысит свое максимальное значение (в справочниках это значение и приводится). то есть предметы на скатерти просто связаны трением покоя со скатертью — поэтому и движуться если медленно тянуть
    Если резко дернуть, то предметы остануться на месте — подумайте над этим
    
    NIN
    24.04.2017 23:18
    #10189400
    Нет, не путаю :), я просто отвечал на утверждение о невозможности ускорения под действием силы трения.
    Тем не менее, сила трения скольжения/качения также может приводить к ускорению тела.
    Представьте движущуюся горизонтальную беговую дорожку, на которую кладут некоторое тело (плоское, или, например, шар). В начальный момент времени скорости полотна и тела (ноль) разные — т.е. на тело действует (и ускоряет) именно сила трения скольжения/качения, которая потом переходит в силу трения покоя, когда скорости полотна и тела сравниваются.
    
    sbnur
    25.04.2017 07:08
    #10189568
    В определение сказано про относительное перемещение соприкасающихся тел
    В вашем случае имеем, что тело положенное на дорожку исходно имеет относительную скорость равную скорости дорожки, но противоположное по направлению, которая за счет трения уменьшается до нуля относительно дорожки.
    Других взаимодействующих тел здесь нет, и движение тела относительно вас значения не имеет
    
    Zenitchik
    25.04.2017 12:28
    #10190050
    +2
    Если я потяну за скатерть достаточно сильно, чтобы предметы на ней начали проскальзывать, они, тем не менее, будут ускоряться силой трения.
    
    Если резко дернуть, то предметы остануться на месте — подумайте над этим
    
    На месте с какой точностью? Ага. Вот оно ваше понимание.
    
    sbnur
    25.04.2017 14:58
    #10190410
    -1
    Почитайте хотя бы википедию, если вам чтение учебников по общей физике недоступно

master65
24.04.2017 09:23
#10188040
Заклинание в Героях тоже надо переименовать в «отрицательное ускорение»

ACPrikh
24.04.2017 14:32
#10188602
«Замедление» так же неверно, как и «ускорение». Вопрос в знаке. Тогда уж «изменение скорости». Да и скорость туда же. Ускорение это «изменение изменения положения».
Вы хотя бы вики почитали «трение качения». Трение не может быть причиной движения в смысле ускорения. Это диссипативная сила по определению.
1. maisvendoo
  24.04.2017 14:33
  #10188604
  +1
  «Замедление» так же неверно, как и «ускорение». Вопрос в знаке
  
  Да нет знака у вектора!
  1. ACPrikh
    24.04.2017 15:57
    #10188788
    -1
    Да есть у векторов направления!
    А как насчет проекций векторов? Вдруг вспомнили, что величины могут быть векторными?
    А давайте об электричестве с учетом его описания в комплексных числах! А давайте рассмотрим качение колеса с учётом тензора напряжений в нём!
    
    maisvendoo
    24.04.2017 16:24
    #10188842
    +1
    А как насчет проекций векторов?
    
    проекция вектора != вектор
    
    проекция вектора это псевдоскаляр
    
    Да есть у векторов направления!
    
    знак числа и направление вектора вещи совершенно разные
    
    не бывает векторов «положительных» и векторов «отрицательных». Не бывает, понимаете?
    
    А давайте об электричестве с учетом его описания в комплексных числах!
    
    Понадобится описывать цепи переменного тока, будут и комплексные числа.
    
    К чему вообще был этот вопль пафоса?
    
    ACPrikh
    25.04.2017 10:37
    #10189808
    Не бывает у машины тормозов. Есть только вектор двигателя. Не бывает скаляров есть только псевдоскаляры. Вы, случайно, не из ветки про «люси ин зе скай виз зе даймондз»?
    
    Есть и замедление, и скаляры, и на векторах свет клином не сошёлся. А попытки надувать щечки только водят в когнитивный диссонанс.
    
    С тех пор перестали малютки играть,
    Не рылись в грязи и в пыли.
    И всё оттого, что не смели визжать,
    А хрюкать они не могли!
    Мой мальчик! Тебе эту песню дарю.
    Рассчитывай силы свои.
    И, если сказать не умеешь «хрю-хрю»,
    — Визжи, не стесняясь: «И-и!»
    
    maisvendoo
    25.04.2017 15:01
    #10190414
    +1
    Не бывает у машины тормозов. Есть только вектор двигателя. Не бывает скаляров есть только псевдоскаляры. Вы, случайно, не из ветки про «люси ин зе скай виз зе даймондз»?
    
    После оценки тона Ваших сообщений, желания метать перед Вами бисер у меня нет. Так что если вы хотите что-то мне сказать, во первых смените тон, а во-вторых погуглите получше и почитайте о разнице между скалярными и псевдоскалярными величинами
    
    ACPrikh
    25.04.2017 15:10
    #10190438
    +2
    Мне не надо читать, чтобы знать, что проекция вектора — это НЕ ПСЕВДОСКАЛЯР. Вы допускаете фактические ошибки одну за другой. При этом претензии на просветление в понимании большей абстракции вектора перед скалярами. Отсюда и тон. Это всего лишь попытка понизить градус Вашего неуместного пафоса.
    
    maisvendoo
    25.04.2017 15:16
    #10190448
    проекция вектора — это НЕ ПСЕВДОСКАЛЯР
    
    Согласен, ошибочка вышла. И вообще говоря, не ошибается тот кто ничего не делает и не о чем не думает. Но проекция вектора и НЕ СКАЛЯР.
    
    Отсюда и тон
    
    Переход на визг не оправдание, при любой степени компетентности оппонента. Так что слюни лучше подберите, а то захлебнетесь

martin_wanderer
24.04.2017 16:13
#10188824
Предлагаю заодно отказаться от понятия «вычитание»…
1. maisvendoo
  24.04.2017 16:26
  #10188846
  Так для векторов и нет понятия «вычитание». Есть две линейных операции над векторами
  
  1. Сложение
  2. Умножение на число
  
  Вычитание есть комбинация двух упомянутых операций
  1. ACPrikh
    25.04.2017 10:42
    #10189820
    А Вы знаете, что если для скорости ещё можно применять векторы, то для ускорения правильным будет применение тензора? В конечном счёте тензор ускорений — антисимметричный тензор, описывающий ускорение, состоящий из шести компонент. При этом данные компоненты являются компонентами двух трёхмерных векторов – напряжённости поля ускорений, и соленоидального вектора ускорений.
    А ваш вектор ускорения — псевдовектор?
    P.S.
    Кстати, вычитание — частный случай сложения. Комбинации операций не требуется. Это залёт, воин векторного исчисления!
    
    metalhand
    25.04.2017 14:58
    #10190412
    вектор это всего лишь частный случай тензора, понятие вектора избыточно и не нужно, оно только все усложняет и запутывает ;)
    
    ACPrikh
    25.04.2017 15:02
    #10190418
    Да-да! Вектор — это вульгарно. Тензор — наше фсё!