1. Введение

В [1] был дан ответ на вопрос, что считать автоматным программированием (АП), но не была подробно описана модель конечного автомата (КА) в качестве модели управления автоматных программ. При этом понятно, что чистый абстрактный автомат на эту роль не годится, т.к. ограничен числом каналов. Но и структурная модель автомата, как и соответствующая ей теория структурных автоматов, не позволяют пока дать ответ по выбору модели автомата.

Проблема начинается с того, что среди множества работ по теории конечных автоматов (ТКА) мало дающих определение модели структурного конечного автомата (СКА). Правда, можно понять, что структурный автомат — это [структурная] схема из элементарных автоматов (функциональных элементов), реализующая модель абстрактного автомата [2]. Напомним, что в соответствии с теорией все начинается с создания модели устройства в форме абстрактного автомата, а затем ставится задача синтеза цифровой схемы, которая его реализует [3].

Программирование на первый взгляд мало похоже на синтез цифровых схем. Но только на первый. Во-первых, там и там все начинается с алгоритма. Во-вторых, структурные вопросы организации и реализации цифровых схем и программирования имеют много общего, особенно в контексте параллельного программирования. Но тему параллелизма мы еще обсудим отдельно. Пока же наша задача выбрать и/или доработать модель конечного автомата, которая была бы понятна, удобна и приятна программистам, избалованных разнообразным программным инструментарием.

Правда, тут же закономерен вопрос — зачем еще один и довольно необычный «автоматный инструментарий»? На этот вопрос мы и попробуем ответить, дав определение модели [вложенного] автоматного управления, рассмотрев также ее преимущества по сравнению с обычной моделью программирования.

2. Определение модели управления автоматных программ

В процессе эволюции практика программирования сформировала определенные требования к модели управления программ. Необходимо признать, что модель классического конечного автомата довольно мало им соответствует. И если уж стоит задача использовать автоматы в программировании, то ее необходимо адаптировать. Сделать желательно это в рамках теории автоматов. Основные претензии к существующему АП сводятся к тому, что это условие нарушается.

Определение 1. Назовем дизъюнктивной нормальной формой конечных автоматов (ДНКА) полностью определенные конечные автоматы, переходы которых помечены элементарными конъюнкциями логических переменных.

Модель ДНКА базируется на формальных моделях полностью (вполне) определенных автоматов с абстрактным состоянием [4] и логических автоматов [5].

Определение 2. Назовем дизъюнктивной формой конечного автомата (ДКА) автомат в форме ДНКА, содержащий только результативные переходы.

К результативными переходами отнесем переходы, помеченные выходными сигналами и переходы с прочерком на месте выходных сигналов, изменяющие текущее состояние автомата. Переходы, которые не включены в описание дизъюнктивного автомата, составляют дополнение ДКА (ДДКА) до полностью определенного автомата ДНКА. Такое дополнение представляет автомат, состоящий из изолированных состояний с переходами в виде петель и с прочерками на месте выходных сигналов.

3. Модель памяти для модели вычислений АП

Наличие множества входов и выходов ДКА задает параллелизм сопоставленных им программных операторов/функций. Для его корректной реализации необходима модель памяти типа CREW (concurrent read exclusive – write) [6]. В ее рамках чтение текущих значений данных разрешено со стороны множества всех функций (предикатов и действий), а изменение общих данных для параллельно исполняемых действий разрешено только одному из них.

Автоматная модель управления в отличие от модели многопоточных вычислений четко ограничивает исполнение операторов/функций автоматной программы границами такта дискретного времени. В такой ситуации любые изменения памяти действиями, исполняемыми на текущем такте, можно записываться в «теневую память», чтобы после их завершения и до начала следующего дискретного такта стать ее новыми значениями.

Взаимодействие операторов автоматной программы с памятью далее будем называть теневой моделью памяти. Данная модель является существенной частью общей модели автоматного программирования. Она гарантирует корректность параллельной работы операторов АП и упрощает программирование параллельных процессов.

В рамках модели памяти фактически не нужны сложные и не очень надежные механизмы многопоточной синхронизации работы процессов (подробнее см. [7]). Но в случае необходимости в силу эквивалентности автоматов и граф-схем алгоритмов (ГСА) [8] модель автоматного программирования не ограничивает и их применение.

4. Вложенная и инерционная модели автоматов

Выбранная далее в качестве примера задача создания модели логического элемента задержки, с одой стороны, демонстрирует проблемы классической модели автомата, а, с другой стороны, отражает качества модели ДКА, решающей алгоритмические задачи более наглядными и удобными средствами. Введенная модель вложенных автоматов порождает подкласс автоматных моделей, названных далее инерционными автоматами, и соответствующий ему подкласс инерционных алгоритмов.

Итак, пусть стоит задача создания дискретной модели логического элемента задержки, реализующего передачу двоичного входного сигнала. При этом времена его задержек t01 и t10 соответственно в единичное и нулевое состояния в общем случае не совпадают.

Простейшая модель единичной задержки в форме автомата Мили показана на рис. 1 (см. для сравнения модель задержки в [2]). Ее задержки определяются единичным дискретным тактом. Более сложные модели транспортных задержек (подробнее о типах задержек см. [9]) в форме автомата Мили и совмещенной модели Мили-Мура представлены соответственно на рис. 2а и рис. 2б.


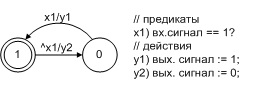
Рис. 1. Модель единичной задержки в форме автомата Мили


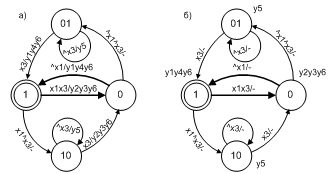
Рис. 2. Модель транспортной задержки Мили(а) и Мили-Мура (б)

Входной сигнал x3 (напомним, в автоматной программе ему соответствует предикат [1]) принимает истинное значение при равенстве значения счетчика тактов значению переменной t, равной величине задержек t01или t10. Значение переменной t присваивают сигналы y3 и y4 (в программе — одноименные выходным сигналам функции-действия). Сигналы y1, y2 устанавливают значение переменной, представляющей выход модели. Сигнал y5 увеличивает счетчик тактов, который сбрасывается сигналом y6.

Замечание 2. Внутренние состояния модели на рис. 1 удобно ассоциировать с состоянием выхода элемента. Это позволяет исключить не только операторы y1 и y2, но и саму переменную выхода.

Реализация вложения автоматов аналогичного вызову подпрограмм формирует технологию модульного автоматного программирования. При этом на программном уровне, в отличие от аналогичных попыток на аппаратном уровне (см. для сравнения [10]), сделать это много проще. Для этого в действие нужно вставить программный вызов вложенного автомата, а затем ядро реализации автоматов подобно обычному процессору организует возврат управления на текущий уровень вложенности.

Определение 3. Вложенными автоматами будем называть автоматы, имеющие заключительное состояние, переход в которое запускает процедуру возврата на предыдущий уровень (ранг) вложенности.

Корректная реализация вложенности автоматов накладывает ограничения на процедуру их создания. Во-первых, вложенный автомат может быть только подчиненным. При этом автомат верхнего уровня, исключая нулевой ранг, может быть также вложенным автоматом. Во-вторых, на любом переходе может быть создан только один вложенный автомат. Механизм вложенных автоматов также создает основу для реализации рекурсивных алгоритмов на базе автоматного управления.


Рис. 3. Модель задержки в форме вложенных автоматов

На рис.3 показана модель задержки, где рис.3а представляет модель верхнего уровня, а рис.3б и рис. 3в – варианты вложенных автоматов для транспортной и инерционной задержки (подробнее о типах задержек см. [8]). Одновременно это примеры двух типов вложенных автоматов – обычного и инерционного. Тип вложенного автомата задается именем его заключительных состояний: состояние с именем «00» определяет обычный выход из вложенного автомата, а состояние с именем «ХХ» не изменяет текущее состояние автомата верхнего уровня.

Важное пояснение для понимания алгоритма работы инерционной задержки. Для нее (см. рис. 3в) значение предиката x1 зависит от перехода, на котором создан вложенный автомат. Другими словами, предикат в состоянии «0» контролирует сохранение «нуля» на входе, а в состоянии «1» наоборот — «единицы». Если значение на входе равно нулю при нулевом значении выхода, то нужно возвращать истинное значение. Далее, если стабильность входа нарушена (значение x1 равно false) и время задержки не истекло (значение x3 — false), то выход из вложенного автомата реализуется через инерционное состояние (см. рис. 3в).

Определение 4. Автоматы, включающие вызов вложенных автоматов, у которых есть заключительное инерционное состояние, будем называть инерционными автоматами.

У модели на рис.3а действие z1 (символ z выбран для имен действий, включающих вызов вложенного автомата) создает вложенный автомат в том случае, если определено значение задержки. В рамках этого действия определяется заданный тип задержки, в соответствии с которым создается один из вложенных автоматов, представленных на рис.3б или рис. 3в.

На верхнем уровне иерархии вид автомата рис.3а по структуре полностью совпадает с моделью на рис.1, отличаясь лишь наличием действий на переходах. Задержки с вложенными автоматами имеют более простой вид в сравнении с одноуровневой моделью на рис.2. Вложенный автомат может рассматриваться и как некий «библиотечный автомат», который может быть вызван из любого другого автомата.

3. Объектное автоматное программирование

Автоматная модель управления, кроме графической формы, имеет и простую табличную форму — таблицу переходов (ТП), которую можно эффективно интерпретировать на языке С++. В его рамках отдельную автоматную программу (или ее часть) и, соответственно, ее определение в форме схемы программы S можно представлять классом. В этом случае модели памяти будут соответствовать свойства класса, множеству операций – методы класса, а автоматное управление в форме ТП будет описывать поведения класса. Введение управления в класс позволяет говорить об активных объектах, называемых также часто агентами и т.п.

Множество объектов с поведением в форме автоматного управления формализует понятие объектной автоматной параллельной программы. В этом случае модель любой параллельной программы может быть представлено схемой программы, в которой управление C будет представлено в форме автоматной сети, где компонентные автоматы описывают поведение активных объектов, память M представлено объединением свойств объектов, а множество операторов A – объединением методов объектов программы.

В среде ВКПа роль языка автоматного программирования возложена на язык С++. В «автоматном С++» объекты наделены активностью/поведением и имеют средства описания и реализации параллелизма, как на уровне методов отдельных объектов, так и на уровне описания параллельной работы множества объектов.

Существующие объектные реализации АП довольно сложны. В ВКПа его объектная реализация базируется на интерпретации автоматов и выделенном управлении программы. В отличие от прямой реализации автоматов, используемой, например, в SWITH-технологии, это исключает процедуру преобразования модели автомата в модель блок-схем. Используемый в ВКПа алгоритм интерпретации аналогичен методу интерпретации таблиц решений Э. Хамби [12].

Если это не оговорено отдельно, мы далее будем ассоциировать понятие автоматной программы с понятием автоматного объекта (АО) в смысле ООП, но с учетом введенного выше понятия объектной автоматной параллельной программы. В силу этого операторы и память АП будем определять через методы и свойства активных объектов. От обычных объектов автоматные объекты отличает наличие поведения, определяемого моделью конечного автомата.

4. Выводы

Создание модели вложенных автоматов — шаг к качественному изменению технологии программирования. Описанная инерционная модель автомата аналогична понятию исторических состояний в UML. Обычное вложение автоматов имеет аналог в программировании, «инерционное вложение» его не имеет, т.к. в программе нельзя вернуться на команду, предшествующую вызову подпрограммы. А это уже элементы качественного отличия автоматного программирования от обычного.

Можно, конечно, и в обычное программирование ввести теневую память и обозначить параллелизм функций. Но в рамках автоматной модели все это имеет органичную форму, как с точки зрения описания, так и с точки зрения исполнения. Все определяется естественным параллелизмом модели. У модели блок-схем таких возможностей нет.

Активные объекты также расширяют возможности программирования. Но и «объектная обертка» со своей стороны качественно влияет на программирование автоматное, упрощая процедуры вызова и реализации вложенных автоматов. Так, использование [локальных] свойств класса позволяет реализовать не просто вложение, а и любые рекурсивные алгоритмы.