Оживляем гексапода. Часть вторая / forpes.ru

Главная
Оживляем гексапода. Часть вторая

Оживляем гексапода. Часть вторая +10

26.02.2020 12:33

kylikovskix 4 1800 Источник

Видео двигающегося гексапода

В сравнении с предыдущей публикацией ее предшественница получилась более зрелищная, благодаря большому количеству фотографий. Хочется заполнить пробел в этом вопросе и представить вам несколько видео, на котором запечатлен небольшой тест-драйв робота по квартире.

Управление роботом происходит оператором с телефона через Wi-Fi. Но при просмотре первых двух видео может сложиться обманчивое впечатление, что гексапод обладает зачатками интеллекта. К сожалению, это пока не так…

Далее робот был изгнан с мягкого ковра на достаточно скользкий линолеум, на котором показал неплохой результат.

Реализация движений гексапода

Как было упомянуто в прошлось статье, за реализацию движений робота отвечает класс MotionJob и производные классы, унаследованные от класса Motion.

Класс MotionJob имеет всего всего один публичные метод execute, запускающий заданное движение на исполнение.

int MotionJob::execute(Motion* pMotion)

int MotionJob::execute(Motion* pMotion) {
  if(m_Status == NONE && pMotion != NULL) {
     
     m_pMotion = pMotion;
     m_MotionTime = 0;
     m_TotalTime = m_pMotion->totalTime();
     m_Status = RUNING;
  } else if(pMotion != NULL){
    
    if(m_pMotion->m_pNext != NULL) 
      delete m_pMotion->m_pNext;
      
    m_pMotion->m_pNext = pMotion;
     m_Status = STOPING;
  }
  return S_OK;
}

Его логика довольно проста. В качестве параметра он принимает указатель на объект, описывающий процесс движения. Если на текущий момент на исполнении не было никакого другого движения, то указанное движение становится активным, и оно переходит в состояние выполнения (RUNING). В том случае, когда на исполнении уже было какое-то движение, то его переводим в состояние остановки (STOPING), а новое движение записывается в качестве следующего в поле m_pNext.

ВАЖНО: Принято соглашение, что все объекты унаследованные от Motion подразумевают создание в динамической области памяти (через new)и освобождаются классом MotionJob после завершения движения или его отмены.

Класс MotionJob, будучи унаследованным от AJob, реализует всю магию движения в перекрытом методе onRun, который вызывается с заданной периодичностью в процессе функционирования робота.

void MotionJob::onRun()

void MotionJob::onRun() {

  Vector3D points[FOOTS_COUNT];
  int pose[FOOTS_COUNT][3];
  // если движение не задано, завершаем работу
  if(m_pMotion == NULL)
    return;
  // Положение конечностей робота может быть задано как набор углов каждого сустава,
  // или как массив координат точек в которых должны располагаться концы лап робота.
  // Один из вариантов должен быть реализован.
  int res;
  if(m_pMotion->getPose(min(m_MotionTime, m_pMotion->maxTime()), pose) == S_OK) {
     res = m_pGeksapod->_setPose(pose);
  } else if(m_pMotion->getPose(min(m_MotionTime, m_pMotion->maxTime()), points) == S_OK) {
     res = m_pGeksapod->_setPose(points);
  }
  // обновляем время исполнения текущего движения
  m_MotionTime += MOTION_JOB_PERIOD;
  // если движение ограничено по времени, уменьшаем его на значение,
  // не допуская проваливание в отрицательный диапазон:
  // отрицательное значение m_TotalTime - признак неограниченного по времени движения
  if(m_TotalTime > 0) { 
    m_TotalTime -= MOTION_JOB_PERIOD;
    m_TotalTime = max(0,m_TotalTime); 
  }
  // если время выполнения зацикленного движения истекло, 
  // переводим его в состояние принудительной остановки
  if(m_TotalTime == 0 && m_pMotion->isLooped()) {
     m_Status = STOPING;
  }
  // Не циклическое движение или движении в состоянии остановки 
  // при достижении окончания должно быть завершено и удалено из памяти.
  if( (m_MotionTime - m_pMotion->maxTime() >= MOTION_JOB_PERIOD && (!m_pMotion->isLooped() || m_Status == STOPING)) ) { // время истекло
    // запоминаем указатель на возможное следующее движение
    Motion* pNextMotion = m_pMotion->m_pNext;
    m_pMotion->m_pNext = NULL;
    delete m_pMotion;
    m_pMotion = NULL;
    // и запускаем его
    m_Status = NONE;
    execute(pNextMotion);
  } else if(m_MotionTime - m_pMotion->maxTime() >= MOTION_JOB_PERIOD) {
    // для зацикленного движения не требующего остановки
    // мы сбрасываем счетчик времени и начинаем новый цикл движения
    m_MotionTime = 0; 
  }
}

Приведенный код содержит достаточно комментариев о своей работе, поэтому в качестве дополнения отмечу лишь несколько ключевых моментов:

Класс Motion позволяет нам описать движение робота либо через набор координат точек концов лап гексапода (Vector3D points[FOOTS_COUNT]), либо через набор значений углов поворота его суставов (int pose[FOOTS_COUNT][3]). Поэтому сначала, выполняется попытка получить результат как набор координат. Если попытка оказалась неудачной и метод getPose вернул ошибку реализации, используем второй вариант вызова getPose. Полученный результат мы передаем в метод _setPose, переводя тем самым конечности робота в заданное положение для данного момента времени.
Движения могут носить обычный или цикличный характер. Обычное движение при достижении конца периода времени отведенного на исполнение одного цикла движения (возвращается методом Motion::maxTime()) будет тут же завершено.
Циклические движения будут завершены только после принудительной остановки, которая возникает в момент вызова метода execute (может быть вызван с пустым указателем), или при достижении положительного момента времени, которое отведено на исполнение движения (возвращается методом Motion::totalTime()).

Для описания различных вариантов движения определены следующие классы:

class TransPoseMotion

class TransPoseMotion: public Motion {
  Vector3D m_Pose0[FOOTS_COUNT];  // начальное положение
  Vector3D m_Offset[FOOTS_COUNT];  // вектор перемещения
public:  
  TransPoseMotion(Vector3D begPose[FOOTS_COUNT], Vector3D endPose[FOOTS_COUNT],
        long maxTime, Motion* pNext = NULL);
  int getPose(long time, Vector3D points[FOOTS_COUNT]);
};

class TransAnglesMotion

class TransAnglesMotion: public Motion {
  char m_Pose0[FOOTS_COUNT][3];
  char m_Offset[FOOTS_COUNT][3];
public:  
  TransAnglesMotion(int begPose[FOOTS_COUNT][3], int endPose[FOOTS_COUNT][3],
        long maxTime, Motion* pNext = NULL);
  int getPose(long actionTime, int pose[FOOTS_COUNT][3]);
};

class LinearMotion

class LinearMotion: public Motion {
  // положение конечности в начале (и конце) шага
  Vector3D m_Pose0[FOOTS_COUNT];
  Vector3D m_Offset; // вектор перемещения в результате шага
  int m_Heigth;          // высота подъема конечностей
public:  
  LinearMotion(int heigth, Vector3D pose0[FOOTS_COUNT], Vector3D speed, 
        long maxTime, long totalTime = -1, Motion* pNext = NULL);
  int getPose(long time, Vector3D points[FOOTS_COUNT]);
};

class RotateMotion

class RotateMotion: public Motion {
  // положение конечности в начале (и конце) шага
  Vector3D m_Pose0[FOOTS_COUNT]; 
  Vector3D m_Angles; // углы поворота в результате шага
  int m_Heigth;           // высота подъема конечностей
public:  
  RotateMotion(int heigth, Vector3D pose0[FOOTS_COUNT], Vector3D rotor, 
        long maxTime, long totalTime = -1, Motion* pNext = NULL);
  int getPose(long time, Vector3D points[FOOTS_COUNT]);
};

Класс TransPoseMotion

Класс TransPoseMotion позволяет выполнить перемещение конечностей из одного положения в другое. При создании объекта в конструктор класса передаются координаты точек и период времени, за которой должно быть осуществлено движение.

TransPoseMotion::TransPoseMotion(...)

TransPoseMotion::TransPoseMotion(Vector3D begPose[FOOTS_COUNT],
  Vector3D endPose[FOOTS_COUNT], long maxTime, Motion* pNext) : Motion(maxTime, -1, pNext) {
  for(int i = 0; i < FOOTS_COUNT; i++) {
    m_Pose0[i] = begPose[i];
    m_Offset[i] = endPose[i] - begPose[i];
  }
}

Зная начальное положение и вектор перемещения для каждой конечности, мы без труда в методе getPose можем получить новое положение лап в промежутке времени от 0 до maxTime, выполнив простые линейные вычисления.

int TransPoseMotion::getPose(...)

int TransPoseMotion::getPose(long time, Vector3D points[FOOTS_COUNT]) {
  for(int i = 0; i < FOOTS_COUNT; i++)
    linearFunc(1.0, m_Offset[i], m_Pose0[i], 1.0*time/m_MaxTime, points[i]);
}

Линейные вычисления возлагаются на вспомогательную функцию linearFunc, которая представляет собой обычное линейное уравнение с параметрами, задаваемыми через аргументы функции.

void linearFunc(...)

void linearFunc(float a, Vector3D offset, Vector3D p0, float k,  Vector3D& res) {
  res = a*offset*k + p0;
}

Класс TransAnglesMotion

Логика данного класса аналогична предыдущему. Отличие заключается лишь в том, что в классе TransAnglesMotion положения конечностей гексапода задаются набором углов, на которые должны быть согнуты его суставы, а не пространственными координатами концов лап робота.

TransAnglesMotion::TransAnglesMotion(...)

TransAnglesMotion::TransAnglesMotion(int begPose[FOOTS_COUNT][3],
  int endPose[FOOTS_COUNT][3], long maxTime, Motion* pNext) : Motion(maxTime, -1, pNext) {
  for(int i = 0; i < FOOTS_COUNT; i++) {
    for(int j = 0; j < 3; j++) {
      m_Pose0[i][j] = begPose[i][j];
      m_Offset[i][j] = endPose[i][j] - begPose[i][j];
    }
  }
}

int TransAnglesMotion::getPose(...)

int TransAnglesMotion::getPose(long time, int pose[FOOTS_COUNT][3]) {
  for(int i = 0; i < FOOTS_COUNT; i++) {
    for(int j = 0; j < 3; j++) 
      pose[i][j] = m_Pose0[i][j] + (int)(1.0*m_Offset[i][j]*time/m_MaxTime);
  }
  return S_OK;
}

Класс LinearMotion

Реализация прямолинейного движения требует немного большего объема кода и вашего внимания. Конструкция гексапода имеет оптимальное количество конечностей, позволяя при движении всегда иметь три точки опоры, таким образом, чтобы проекция центра масс робота всегда располагалась внутри образованного ими треугольника. Это обеспечивает устойчивое положение робота при движении. Поэтому прямолинейное движение робота можно рассматривать как множество одинаковых шагов. В каждом таком шаге можно можно выделить две фазы. В первой фазе одна триада ног касается поверхности и их окончания перемещаются параллельно поверхности в направлении противоположном направлению движения. При этом вторая триада лап, не касаясь поверхности, по криволинейной траектории двигается в направлении движения робота. В определенный момент времени они достигают своего крайнего положения, и вторая триада начинает соприкасаться с поверхностью. Во в второй фазе процесс движения повторяется, только на это раз вторая триада выполняет перемещение робота, а первая возвращается в исходную точку.

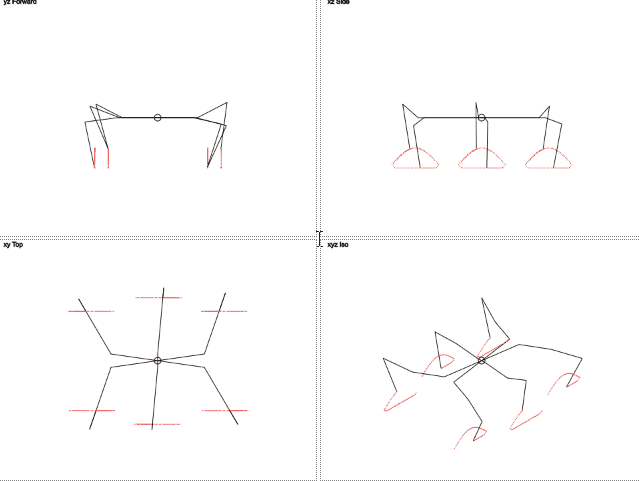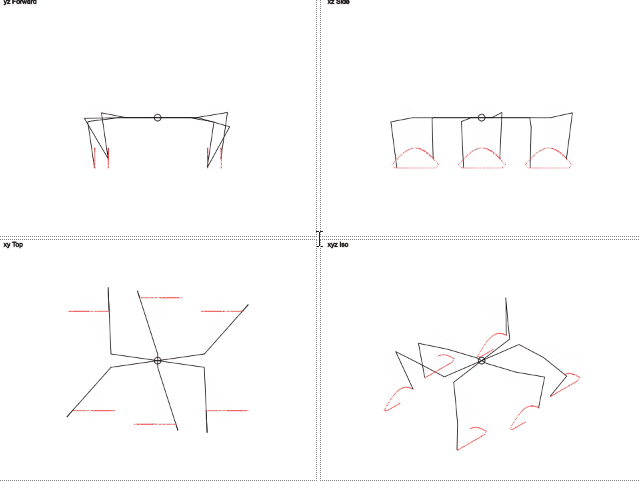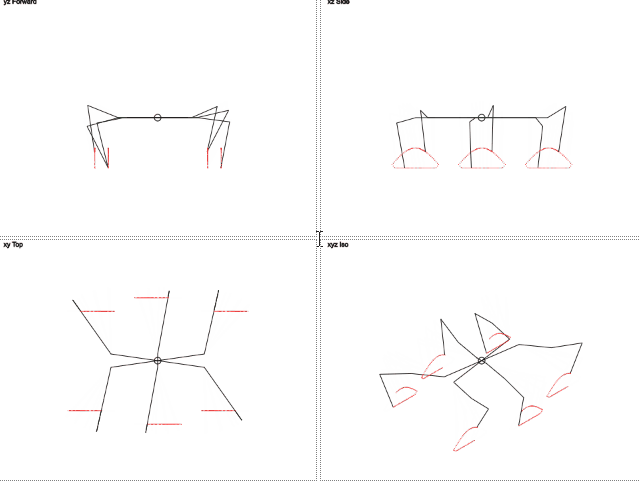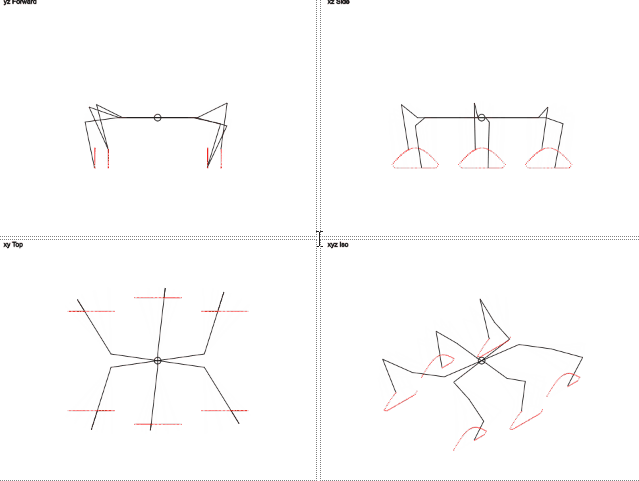
Данная анимация была найдена при подготовке статьи в просторах интернета на этой странице, но после ознакомления с ней я убедился, что ее первоначальным источником был habr, а автором публикации является уважаемый conKORD.

При реализации движения по прямой нам необходимо задать высоту отрыва лап от поверхности (heigth), положение конечностей робота в начале (и в конце) движения (pose0), вектор скорости (speed), время выполнения одного шага (maxTime) и сколько времени робот должен выполнять движение (totalTime). Если указать отрицательное значение totalTime, движение будет выполняться бесконечно пока не кончится заряд робота или движение не будет принудительно завершено.

LinearMotion::LinearMotion(...)

LinearMotion::LinearMotion(int heigth, Vector3D pose0[FOOTS_COUNT], Vector3D speed,
  long maxTime, long totalTime, Motion* pNext = NULL) 
    : Motion(maxTime, true, totalTime, pNext) {
  copyPose(m_Pose0, pose0);
  m_Offset = 1.0*speed*maxTime/1000;
  m_Heigth = heigth;
}

Несмотря на то, что метод getPose содержит внушительный объем кода, он достаточно прост.

int LinearMotion::getPose(...)

int LinearMotion::getPose(long time, Vector3D points[FOOTS_COUNT]) {
  double k = 1.0*time/m_MaxTime;

  if(k < 0.25) {  // первая четверть шага
    linearFunc(2.0, -m_Offset, m_Pose0[LEFT_FRONT_FOOT_IDX], k,
      points[LEFT_FRONT_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[LEFT_BACK_FOOT_IDX], k,
      points[LEFT_BACK_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[RIGTH_MIDLE_FOOT_IDX], k,
      points[RIGTH_MIDLE_FOOT_IDX]);

    linearFunc(2.0, m_Offset, m_Pose0[LEFT_MIDLE_FOOT_IDX], k,
      points[LEFT_MIDLE_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[RIGTH_FRONT_FOOT_IDX], k,
      points[RIGTH_FRONT_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[RIGTH_BACK_FOOT_IDX], k,
      points[RIGTH_BACK_FOOT_IDX]);
  
    int h = (int)m_Heigth*cos(M_PI*k*2);
    points[LEFT_MIDLE_FOOT_IDX].z += h;
    points[RIGTH_FRONT_FOOT_IDX].z += h;
    points[RIGTH_BACK_FOOT_IDX].z += h;

  } else if(k < 0.5) { // вторая четверть шага
    
    linearFunc(2.0, m_Offset, m_Pose0[LEFT_FRONT_FOOT_IDX], k - 0.5,
      points[LEFT_FRONT_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[LEFT_BACK_FOOT_IDX], k - 0.5,
      points[LEFT_BACK_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[RIGTH_MIDLE_FOOT_IDX], k - 0.5,
      points[RIGTH_MIDLE_FOOT_IDX]);

    linearFunc(2.0, -m_Offset, m_Pose0[LEFT_MIDLE_FOOT_IDX], k - 0.5,
      points[LEFT_MIDLE_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[RIGTH_FRONT_FOOT_IDX], k - 0.5,
      points[RIGTH_FRONT_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[RIGTH_BACK_FOOT_IDX], k - 0.5,
      points[RIGTH_BACK_FOOT_IDX]);

    int h = (int)m_Heigth*sin(M_PI*(k - 0.25)*2);
    points[LEFT_FRONT_FOOT_IDX].z += h;
    points[LEFT_BACK_FOOT_IDX].z += h;
    points[RIGTH_MIDLE_FOOT_IDX].z += h;

  } else if(k < 0.75) { // третья четверть шага
    
    linearFunc(2.0, m_Offset, m_Pose0[LEFT_FRONT_FOOT_IDX], k - 0.5,
      points[LEFT_FRONT_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[LEFT_BACK_FOOT_IDX], k - 0.5,
      points[LEFT_BACK_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[RIGTH_MIDLE_FOOT_IDX], k - 0.5,
      points[RIGTH_MIDLE_FOOT_IDX]);

    linearFunc(2.0, -m_Offset, m_Pose0[LEFT_MIDLE_FOOT_IDX], k - 0.5,
      points[LEFT_MIDLE_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[RIGTH_FRONT_FOOT_IDX], k - 0.5,
      points[RIGTH_FRONT_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[RIGTH_BACK_FOOT_IDX], k - 0.5,
      points[RIGTH_BACK_FOOT_IDX]);
    
    int h = (int)m_Heigth*cos(M_PI*(k - 0.5)*2);
    points[LEFT_FRONT_FOOT_IDX].z += h;
    points[LEFT_BACK_FOOT_IDX].z += h;
    points[RIGTH_MIDLE_FOOT_IDX].z += h;
    
  } else {  // последняя четверть шага
    
    linearFunc(2.0, m_Offset, m_Pose0[LEFT_FRONT_FOOT_IDX], 1 - k,
      points[LEFT_FRONT_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[LEFT_BACK_FOOT_IDX], 1 - k,
      points[LEFT_BACK_FOOT_IDX]);
    linearFunc(2.0, m_Offset, m_Pose0[RIGTH_MIDLE_FOOT_IDX], 1 - k,
      points[RIGTH_MIDLE_FOOT_IDX]);

    linearFunc(2.0, -m_Offset, m_Pose0[LEFT_MIDLE_FOOT_IDX], 1 - k,
      points[LEFT_MIDLE_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[RIGTH_FRONT_FOOT_IDX], 1 - k,
      points[RIGTH_FRONT_FOOT_IDX]);
    linearFunc(2.0, -m_Offset, m_Pose0[RIGTH_BACK_FOOT_IDX], 1 - k,
      points[RIGTH_BACK_FOOT_IDX]);
    
    int h = (int)m_Heigth*sin(M_PI*(k - 0.75)*2);
    points[LEFT_MIDLE_FOOT_IDX].z += h;
    points[RIGTH_FRONT_FOOT_IDX].z += h;
    points[RIGTH_BACK_FOOT_IDX].z += h;
  }

  return S_OK;
}

Весь шаг мы делим на четыре четверти:

В первой четверти, первая триада конечностей (левая передняя, левая задняя и правая средняя) выполняют толкательное движение, то есть они перемещаются по поверхности в направлении противоположном движению. Вторая триада лап (правая передняя, правая задняя и левая средняя) перемещаются в направлении движения, при этом высота их подъема меняется от максимального значения заданной высоты подъема лап (в начале четверти) до нуля (в конце четверти) как функция синуса.
Во второй четверти, направления движения триад меняются. Теперь вторая триада лап выполняет перемещение робота, а первая движется в том же направлении что и робот. При этом высота лап первой триады меняется по синусоиде от нулевого значения до максимального значения.
В третьей четверти направление движения лап сохраняется, а концы первой триады идут на снижение, достигая поверхности в конце третьей четверти.
В последней четверти первая триада становится опорной, а вторая меняет направление и двигается по синусоиде вверх, достигая максимальной высоты подъема в конце четверти.

Класс RotateMotion

Поняв логику работы класса LinearMotion, мы без труда разберемся с реализацией класса RotateMotion.

RotateMotion::RotateMotion(...)

RotateMotion::RotateMotion(int heigth, Vector3D pose0[FOOTS_COUNT], Vector3D speed,
  long maxTime, long totalTime = -1, Motion* pNext = NULL) 
    : Motion(maxTime, true, totalTime, pNext) {
  copyPose(m_Pose0, pose0);
  m_Angles = 0.001*maxTime*speed*M_PI/180;
  m_Heigth = heigth;
}

Конструкторы обоих классов практически идентичны по составу передаваемых аргументов. Только в случае разворота speed — это вектор угловой скорости, задающий ось и скорость вращения робота.

В методе getPose класса RotateMotion логика работы так же подразделена на четыре этапа. Однако для вычисления положения лап вместо линейной функции linearFunc используется радиальная функция rotFunc.

int RotateMotion::getPose(...)

int RotateMotion::getPose(long time, Vector3D points[FOOTS_COUNT]) {
  double k = 1.0*time/m_MaxTime;
  if(k < 0.25) {  // первая четверть шага

    rotFunc(2.0, m_Angles, m_Pose0[LEFT_FRONT_FOOT_IDX], k,
      points[LEFT_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_BACK_FOOT_IDX], k,
      points[LEFT_BACK_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_MIDLE_FOOT_IDX], k,
      points[RIGTH_MIDLE_FOOT_IDX]);
      
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_MIDLE_FOOT_IDX], -k,
      points[LEFT_MIDLE_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_FRONT_FOOT_IDX], -k,
      points[RIGTH_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_BACK_FOOT_IDX], -k,
      points[RIGTH_BACK_FOOT_IDX]);

    int h = (int)m_Heigth*cos(M_PI*k*2);
    points[LEFT_MIDLE_FOOT_IDX].z += h;
    points[RIGTH_FRONT_FOOT_IDX].z += h;
    points[RIGTH_BACK_FOOT_IDX].z += h;

  } else if(k < 0.5) {  // вторая четверть шага
    
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_FRONT_FOOT_IDX], 0.5 - k,
      points[LEFT_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_BACK_FOOT_IDX], 0.5 - k,
      points[LEFT_BACK_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_MIDLE_FOOT_IDX], 0.5 - k,
      points[RIGTH_MIDLE_FOOT_IDX]);
      
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_MIDLE_FOOT_IDX], k - 0.5,
      points[LEFT_MIDLE_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_FRONT_FOOT_IDX], k - 0.5,
      points[RIGTH_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_BACK_FOOT_IDX], k - 0.5,
      points[RIGTH_BACK_FOOT_IDX]);
  
    int h = (int)m_Heigth*sin(M_PI*(k - 0.25)*2);
    points[LEFT_FRONT_FOOT_IDX].z += h;
    points[LEFT_BACK_FOOT_IDX].z += h;
    points[RIGTH_MIDLE_FOOT_IDX].z += h;

  } else if(k < 0.75) {  // третья четверть шага
  
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_FRONT_FOOT_IDX], 0.5 - k,
      points[LEFT_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_BACK_FOOT_IDX], 0.5 - k,
      points[LEFT_BACK_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_MIDLE_FOOT_IDX], 0.5 - k,
      points[RIGTH_MIDLE_FOOT_IDX]);
      
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_MIDLE_FOOT_IDX], k - 0.5,
      points[LEFT_MIDLE_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_FRONT_FOOT_IDX], k - 0.5,
      points[RIGTH_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_BACK_FOOT_IDX], k - 0.5,
      points[RIGTH_BACK_FOOT_IDX]);
  
    int h = (int)m_Heigth*cos(M_PI*(k - 0.5)*2);
    points[LEFT_FRONT_FOOT_IDX].z += h;
    points[LEFT_BACK_FOOT_IDX].z += h;
    points[RIGTH_MIDLE_FOOT_IDX].z += h;
  } else { // последняя четверть шага
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_FRONT_FOOT_IDX], k - 1,
      points[LEFT_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_BACK_FOOT_IDX], k - 1,
      points[LEFT_BACK_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_MIDLE_FOOT_IDX], k - 1,
      points[RIGTH_MIDLE_FOOT_IDX]);
      
    rotFunc(2.0, m_Angles, m_Pose0[LEFT_MIDLE_FOOT_IDX], 1 - k,
      points[LEFT_MIDLE_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_FRONT_FOOT_IDX], 1 - k,
      points[RIGTH_FRONT_FOOT_IDX]);
    rotFunc(2.0, m_Angles, m_Pose0[RIGTH_BACK_FOOT_IDX], 1 - k,
      points[RIGTH_BACK_FOOT_IDX]);

    int h = (int)m_Heigth*sin(M_PI*(k - 0.75)*2);
    points[LEFT_MIDLE_FOOT_IDX].z += h;
    points[RIGTH_FRONT_FOOT_IDX].z += h;
    points[RIGTH_BACK_FOOT_IDX].z += h;
  }
  return S_OK;
}

Радиальная функция позволяет вычислить положение точки в пространстве после ее вращения вокруг центра робота, который совпадает с началом координат.

void rotFunc(...)

void rotFunc(float a, Vector3D angles, Vector3D p0, float k, Vector3D& res) {
  Matrix3D m = rotMatrix2(a*angles*k);
  res = m*p0;
}

Внутри функции задействован математический аппарат, позволяющий нам работать с векторными и матричными величинами.

На этом пока закончить. Мы разобрали существенную часть программного кода, отвечающего за реализацию движения робота. Если остались вопросы или замечания, буду рад ответить на них в комментариях. Следующую статью я постараюсь посвятить оставшейся части кода, исходники которого будут доступны для скачивания.
Спасибо за внимание!

Продолжение следует…

Комментарии (4)

tas
26.02.2020 17:40
#21325290
Супер!

Только вот смотрю я на видео, как он двигается и кажется мне, что коротковатые у него лапки. Сделать бы эти лапки подлиннее, тогда можно было бы достигнуть большей плавности движений, получилось бы намного ближе к природе, что-ли…

А потом положить камеру на пол и снимать как «оно» ползет — готовый фильм ужасов :)

muhaa
26.02.2020 23:59
#21326804
Не хватает видео про кота и гексапод.
1. kylikovskix Автор
  27.02.2020 00:32
  #21326892
  Как ни странно кот больше боится пылесоса, чем гексапода.

thenonsense
28.02.2020 14:58
#21333988
Инсектомехосы — это хорошо

немного 3d в тему