Я ещё с университета знал о фильтре Блума — вероятностной структуре данных, названной в честь Бёртона Блума. Но у меня не было возможности её использовать. В прошлом месяце такая возможность появилась — и эта структура буквально очаровала меня. Впрочем, вскоре я нашёл у неё некоторые недостатки. В этой статье — рассказ о моей краткой любовной связи с фильтром Блума.

В процессе исследований IP-спуфинга нужно было проверять IP-адреса в поступающих пакетах, сравнивая их с географическим расположением наших центров обработки данных. Например, пакеты из Италии не должны поступать в бразильский ЦОД. Эта проблема может показаться простой, но в постоянно меняющемся ландшафте интернета это далеко не просто. Достаточно сказать, что в итоге у меня накопилось много больших текстовых файлов примерно такого содержания:



Это значит, что в дата-центре Cloudflare номер 107 зафиксирован запрос с разрешённого IP-адреса 192.0.2.1. Эти данные поступали из многих источников, включая наши активные и пассивные пробы, логи некоторых доменов, которыми мы владеем (например, cloudflare.com), открытые источники (например, таблицы BGP) и т. д. Одна и та же строка обычно повторяется в нескольких файлах.

В итоге я получил гигантский набор данных такого рода. В какой-то момент во всех собранных источниках я насчитал 1 миллиард строк. Обычно я пишу bash-скрипты для предварительной обработки входных данных, но в таком масштабе этот подход не работал. Например, удаление дубликатов из этого крошечного файла на 600 МиБ и 40 млн строк занимает… вечность:



Достаточно сказать, что дедупликация строк обычными командами типа sort в различных конфигурациях (см. --parallel, --buffer-size и --unique) оказалась не самой оптимальной для такого большого набора данных.

Фильтры Блума

Иллюстрация Дэвида Эпштейна в общественном достоянии

Потом меня осенило: не надо сортировать строки! Нужно удалить дубликаты, поэтому гораздо быстрее сработает какая-то структура данных типа 'set' (множество). Кроме того, я примерно знаю объём входного файла (количество уникальных строк), а потеря некоторых данных не критична, то есть вполне подходит вероятностная структура данных.

Это идеальный вариант для фильтров Блума!

Пока вы читаете Википедию о фильтрах Блума, вот как я смотрю на эту структуру данных.

Как бы вы реализовали «множество»? Учитывая идеальную хэш-функцию и бесконечную память, мы можем просто создать бесконечный битовый массив и для каждого элемента установить битовый номер hash(item). Это даёт идеальную структуру данных для «множества». Так ведь? Тривиально. К сожалению, у хэш-функций случаются коллизии, а бесконечной памяти не существует, поэтому в нашей реальности придётся пойти на компромисс. Но мы можем рассчитать вероятность коллизий и управлять этим значением. Например, у нас хорошая хэш-функция и 128 ГБ памяти. Мы можем вычислить, что вероятность коллизии для каждого нового элемента составляет 1 к 1099511627776. При добавлении большего количества элементов вероятность растёт по мере заполнения битового массива.

Кроме того, мы можем применить более одной хэш-функции и получить более плотный битовый массив. Именно здесь хорошо подходит фильтр Блума, который представляет собой набор математических данных с четырьмя переменными:

• n — число вставленных элементов (кардинальное число)
  
• m — память, используемая битовым массивом
  
• k — количество хэш-функций, подсчитанных для каждого входа
  
• p — вероятность ложноположительного совпадения

Учитывая кардинальное число n и желаемую вероятность ложноположительного срабатывания p, фильтр Блума возвращает требуемую память m и необходимое количество хэш-функций k.

Посмотрите эту превосходную визуализацию Томаса Хёрста, как параметры влияют друг на друга.

mmuniq-bloom

Руководствуясь интуицией, я добавил в свой арсенал вероятностный инструмент mmuniq-bloom, который берёт ввод STDIN и возвращает только уникальные строки в STDOUT. Он должен быть гораздо быстрее, чем комбинация sort+uniq!

Вот он:

• mmuniq-bloom.c

Для простоты и для скорости я изначально установил несколько параметров. Во-первых, если не указано иное, mmuniq-bloom использует восемь хэш-функций k=8. Кажется, это близко к оптимальному числу для нашего размера данных, и хэш-функция может быстро выдать восемь приличных хэшей. Затем выравниваем память m в битовом массиве на степень двух, чтобы избежать дорогостоящей операции %modulo, которая в ассемблере сводится к медленному div. Если массив равен степени двойки, мы можем просто использовать побитовое И (для удовольствия почитайте, как компиляторы оптимизируют некоторые операции деления, умножая на магическую константу).

Теперь можем запустить его на том же файле данных, который использовали раньше:



О, это намного лучше! 12 секунд вместо двух минут. Программа использует оптимизированную структуру данных, относительно ограниченный объём памяти, оптимизированный разбор строк и хорошую буферизацию выходных данных… и при всём этом 12 секунд кажутся вечностью по сравнению с инструментом wc -l:



Что происходит? Я понимаю, что подсчёт строк в wc проще, чем вычисление уникальных строк, но действительно ли оправдана разница в 26 раз? На что уходит CPU в mmuniq-bloom?

Должно быть, на вычисление хэшей. Утилита wc не тратит процессор, выполняя всю эту странную математику для каждой из 40 млн строк. Я использую довольно нетривиальную хэш-функцию siphash24, наверняка это она сжигает процессор, верно? Давайте проверим, запустив только хэш-функцию, но не выполняя никаких операций с фильтром Блума:



Это странно. Вычисление хэш-функции занимает всего около двух секунд, хотя вся программа в предыдущем запуске выполнялась 12 секунд. Неужели один фильтр Блума работает 10 секунд? Как такое возможно? Это же такая простая структура данных…

Секретное оружие — профайлер

Пришло время применить для этой задачи правильный инструмент — давайте запустим профайлер и посмотрим, над чем работает процессор. Во-первых, запустим strace для проверки, что отсутствуют какие-то неожиданные системные вызовы: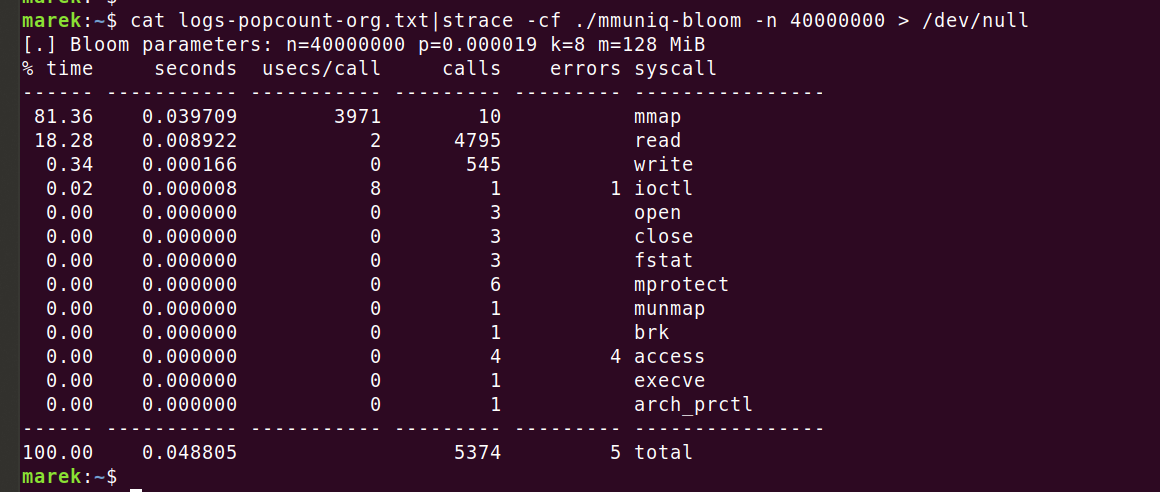



Всё выглядит хорошо. Десять вызовов к mmap по 4 мс (3971 мкс) интригуют, но это нормально. Предварительно заполняем память с помощью MAP_POPULATE, чтобы позже предотвратить ошибки из-за отсутствия страницы.

Каков следующий шаг? Конечно, это perf!



Затем посмотрим результат:



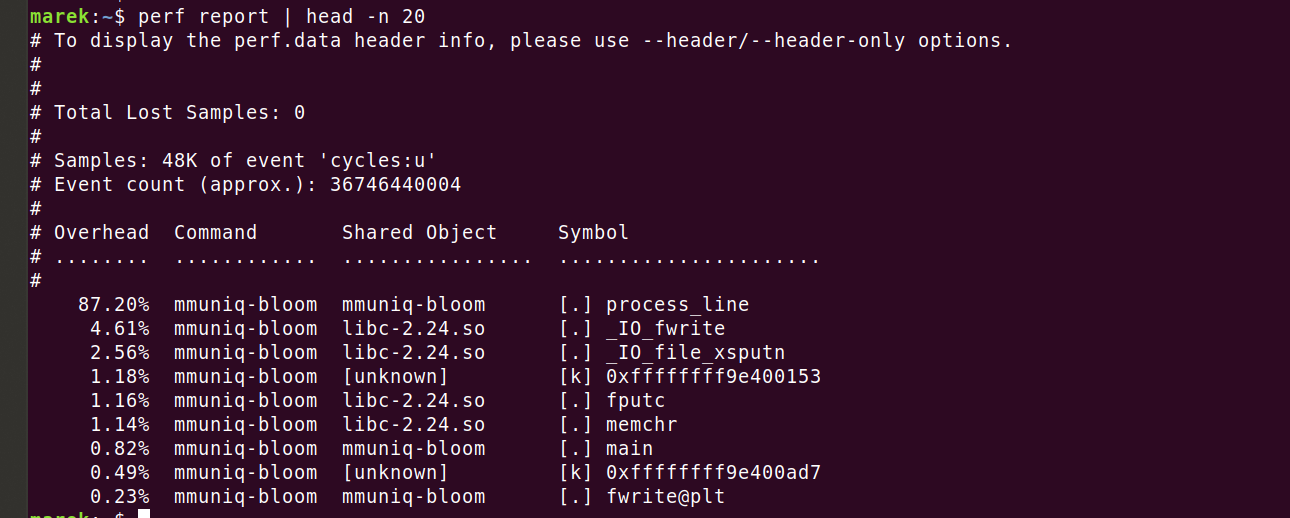
Итак, мы действительно сжигаем 87,2% циклов в основном коде. Посмотрим, где именно. Команда perf annotate process_line --source сразу показывает нечто неожиданное.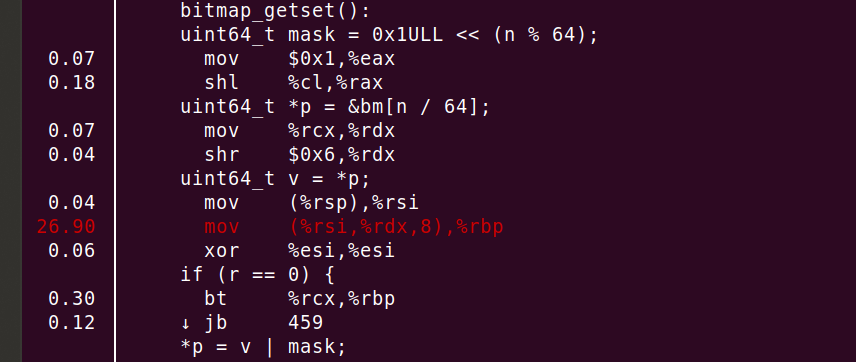



Мы видим, что 26,90% процессора сгорело в mov, но это ещё не всё! Компилятор правильно вставляет функцию и разворачивает цикл. Получается, что большинство циклов уходит на этот mov или на строку uint64_t v = *p!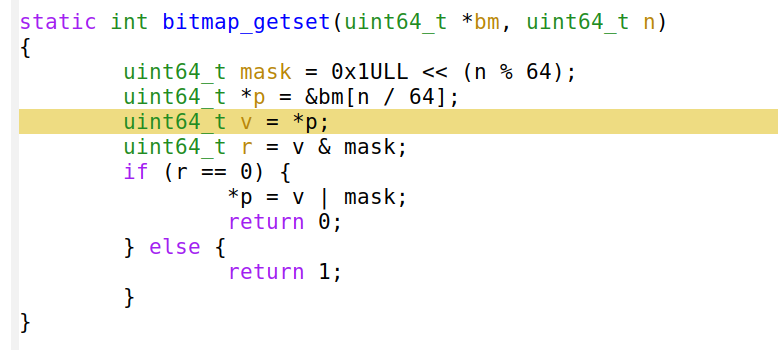



Очевидно, perf ошибается, как такая простая строка может отнимать столько ресурсов? Но повторение теста с любым другим профайлером показывает ту же проблему. Например, мне нравится использовать google-perftools с kcachegrind из-за красочных диаграмм:



Результат визуализации выглядит следующим образом:



Позвольте подытожить, что мы обнаружили к настоящему моменту.

Стандартная утилита wc обрабатывает файл 600 МиБ за 0,45 с процессорного времени. Наш оптимизированный инструмент mmuniq-bloom работает 12 секунд. Процессор сжигается на одной инструкции mov, разыменовывая память…


Изображение Хосе Никдао, CC BY/2.0

О! Как же я мог забыть. Случайный доступ к памяти — действительно медленная штука! Очень, очень, очень медленная!

Согласно числам, которые должен знать каждый программист, одно обращение к RAM занимает около 100 нс. Давайте посчитаем: 40 миллионов строк, по 8 хэшей на каждую. Поскольку у нашего фильтра Блума размер 128 МиБ, на нашем старом железе он не помещается в кэш L3! Хэши равномерно распределены по большому диапазону памяти — каждый из них генерирует промах кэша. Сложим всё вместе, и получается…



Выходит, что 32 секунды сгорают только на обращениях к памяти. Реальная программа укладывается всего в 12 секунд, поскольку фильтр Блума всё-таки извлекает определённую пользу от кэширования. Это легко увидеть с помощью perf stat -d:



Да, у нас должно было быть минимум 320 млн промахов кэша (LLC-load-misses), но случилось только 280 млн: это по-прежнему не объясняет, почему программа сработала всего за 12 секунд. Но это не имеет значения. Важно, что количество промахов кэша — это реальная проблема, и мы можем решить её лишь сократив количество обращений к памяти. Попробуем настроить фильтр Блума на использование только одной хэш-функции:



Ай! Это действительно больно! Чтобы получить вероятность коллизий 1 на 10 000 строк, фильтр Блума потребовал 64 гигабайта памяти. Это ужасно!

Кроме того, не похоже, что скорость сильно выросла. Операционной системе потребовалось 22 секунды, чтобы подготовить для нас память, но мы всё равно потратили 11 секунд в пользовательском пространстве. Полагаю, что теперь все преимущества более редкого обращения к памяти компенсируются более низкой вероятностью попадания в кэш из-за резко увеличенного объёма памяти. Раньше фильтру Блума хватало 128 МиБ!

Отказ от фильтров Блума

Это становится просто смешно. Чтобы снизить вероятность ложноположительных срабатываний, нужно или использовать много хэшей в фильтре Блума (например, восемь) с большим количеством обращений к памяти, или оставить одну хэш-функцию, но задействовать огромные объёмы памяти.

У нас на самом деле нет ограничения на память, мы хотим минимизировать количество обращений к ней. Нам нужна структура данных, которая обходится максимум одним промахом кэша на элемент и использует менее 64 гигабайт оперативной памяти…

Конечно, можно внедрить сложные структуры данных, такие как фильтр кукушки, но наверняка есть вариант попроще. Что насчёт старой доброй хэш-таблицы с линейным зондированием?


Иллюстрация Вадимса Поданса

Встречаем mmuniq-hash

Вот новая версия mmuniq-bloom, с использованием хэш-таблицы:

• mmuniq-hash.c

Вместо битов для фильтра Блума мы теперь храним 64-битные хэши из функции 'siphash24'. Это обеспечивает гораздо лучшую защиту от коллизий хэша: намного лучше, чем одна на 10 000 строк.

Давайте посчитаем. Добавление нового элемента в хэш-таблицу, скажем, с 40 млн записей, даёт вероятность коллизии хэшей 40 000 000/2^64. Это примерно 1 к 461 миллиардам — достаточно низкая вероятность. Но мы не добавляем один элемент в предварительно заполненное множество! Вместо этого мы добавляем 40 млн строк в изначально пустое множество. Согласно парадоксу дней рождения, это сильно повышает вероятность коллизии. Разумным приближением будет оценка '~n^2/2m, в нашем случае это ~(40M^2)/(2*(2^64)). Получается один шанс из 23 000. Другими словами, с хорошей хэш-функцией мы ожидаем коллизии в одном из 23 000 случайных множеств по 40 миллионов элементов. Это ненулевая вероятность, но всё же лучше, чем в фильтре Блума, и она полностью терпима для нашего случая использования.

Код с хэш-таблицей работает быстрее, у него лучше шаблоны доступа к памяти и ниже вероятность ложноположительных срабатываний, чем в фильтре Блума.



Не пугайтесь строки «конфликты хэшей», она просто показывает, насколько заполнена хэш-таблица. Мы используем линейное зондирование, поэтому при попадании в полный набор просто берём следующий пустой. В нашем случае приходится пропускать в среднем 0,7 наборов, чтобы найти пустое место в таблице. Это нормально. Поскольку мы перебираем наборы в линейном порядке, память должна качественно заполняться.

Из предыдущего примера мы знаем, что наша хэш-функция выполняется около двух секунд. Делаем вывод, что 40 млн обращений к памяти занимают около четырёх секунд.

Усвоенные уроки

Современные процессоры действительно хороши в последовательном доступе к памяти, когда можно предсказать шаблоны выборки (см. предварительную выборку кэша). С другой стороны, случайный доступ к памяти обходится очень дорого.

Продвинутые структуры данных очень интересны, но будьте осторожны. Современные компьютеры требуют использования алгоритмов, оптимизированных для кэша. При работе с большими наборами данных, которые не помещаются в L3, предпочтение отдаётся оптимизации на количество обращений, а не оптимизации на объём используемой памяти.

Справедливо сказать, что фильтры Блума великолепно себя проявляют, пока помещаются в кэш L3. Но если нет, то они ужасны. Это не новость: фильтры Блума оптимизированы на объём памяти, а не на количество обращений к ней. Например, смотрите научную статью по фильтрам кукушки.

Другое дело — бесконечные дискуссии о хэш-функциях. Честно говоря, в большинстве случаев это не имеет значения. Стоимость подсчёта даже сложных хэш-функций вроде siphash24 невелика по сравнению со стоимостью случайного доступа к памяти. В нашем случае упрощение хэш-функции принесёт лишь небольшую выгоду. Процессорное время просто тратится где-то в другом месте — в ожидании памяти!

Один коллега часто говорит: «Можно предположить, что современные процессоры бесконечно быстры. Они работают с бесконечной скоростью, пока не упираются в стену памяти».

Наконец, не повторяйте мою ошибку. Всегда нужно сначала выполнить профилирование с perf stat -d и посмотреть на счётчик IPC (инструкций на цикл). Если он меньше единицы, обычно это означает, что программа застряла в ожидании памяти. Оптимальны значения выше двух. Это означает, что рабочая нагрузка в основном идёт на CPU. К сожалению, в моих задачах IPC по-прежнему невысок…

Улучшенный mmuniq

При помощи коллег я написал улучшенную версию инструмента mmuniq на основе хэш-таблицы. Вот код:

• mmuniq.c

Он умеет динамически изменять размер хэш-таблицы, поддерживает входные данные с произвольным кардинальным числом. Затем обрабатывает данные пакетами, эффективно используя хинт prefetch в CPU, что ускоряет программу на 35-40%. Будьте осторожны, обильное использование prefetch в коде редко даёт эффект. Чтобы воспользоваться этой функцией, я специально изменил порядок алгоритмов. Со всеми улучшениями время выполнения сократилось до 2,1 секунды:

Конец

Создание базового инструмента, который пытается превзойти по скорости комбинацию 'sort/uniq', выявило некоторые скрытые особенности современных вычислений. Немного попотев, мы ускорили программу с более чем двух минут до двух секунд. Во время разработки мы узнали о задержке случайного доступа к памяти, а также о мощи структур данных, дружественных к кэшу. Причудливые структуры данных привлекают внимание, но на практике зачастую эффективнее оказывается уменьшить количество случайных обращений к памяти.