
Несколько лет назад компания Veeam открыла R&D центр в Праге. Изначально у нас был небольшой офис примерно на 40 человек, но компания активно растет, и сейчас, в новом просторном офисе Rustonka нас уже больше двухсот. Veeam нанимает сотрудников не только из Чехии и Евросоюза, но и активно релоцирует успешных кандидатов из России. Многие переезжают вместе с женой и детьми, и вот тут у них возникает вопрос, с которым я и моя семья столкнулись четыре года назад, когда мы впервые оказались в Праге: нам надо было решить, где выбрать жилье, в какой садик будет ходить дочка, и решить множество других проблем, которые возникали по причине полного незнания города. Конечно, можно проверить всё это своими ногами, но мне захотелось подойти к вопросу с инженерной точки зрения и решить эту задачу с помощью дата-сайнс подхода — с помощью анализа данных в открытом доступе определить наиболее благоприятные для проживания районы Праги.
Определение степени благоприятности района — довольно обширная задача, и оценка может быть весьма субъективна, поэтому для начала, я немного конкретизирую и опишу проблему следующим образом:
Какой район Праги наиболее привлекателен с точки зрения пешеходной доступности инфраструктуры для детей в возрасте от 10 до 16 лет?
Под пешеходной доступностью в своей работе я беру расстояние в 1300 метров. Именно такой порог, согласно различным исследованиям, считается оптимальным для этой возрастной группы.
В качестве объектов инфраструктуры я выбрал такие, которые, по моему мнению, посещает большинство детей. Это школы, библиотеки, образовательные центры, спортивные центры и игровые площадки.
Город и данные
Прага — столица Чешской республики, её культурный и экономический центр. По совместительству это 14й по величине город в Европейском союзе. На площади в 298 кв. км. официально проживает 1,3 миллиона человек.
История Праги насчитывает уже 14 веков. И, как практически любой европейский город, заложенный в раннем средневековье, Прага имеет классическую для этого типа городов топологию. Исторический центр — сравнительно небольшой по площади, с плотной застройкой и узкими улицами. Непосредственно к нему примыкают районы с уже более поздней застройкой, причем, в отличие от самого центра, эти районы неоднократно перестраивались, модернизировались и теперь уже более приспособлены для жизни современного человека. Периферия — спальные районы, плавно переходящие в малоэтажную застройку, и частные дома.
В целом Прага очень комфортна для жизни. Она компактна, в ней нет многоэтажной застройки, нет пробок, удобная сеть общественного транспорта. Но это мое личное мнение, и я не могу утверждать, что оно верно на все 100 процентов, поэтому было интересно посмотреть на город с точки зрения цифр. К слову сказать, Прага занимает лидирующие позиции по доступности городских данных. На портале IPR Praha собрано огромное количество различных наборов данных: демография, экономика, транспорт, медицина, экология и т.п. Данные доступны абсолютно свободно, постоянно обновляются и дополняются.
География и демография
Данные о количественном и качественном составе населения Праги я буду брать из набора данных Чешского Статистического Бюро. Они были собраны в период последней национальной переписи населения и содержат информация о поле, возрасте и количестве жителей по каждому населенному пункту Чешской Республики. Для крупных населенных пунктов — таких, как Прага и Брно — данные также приведены по каждому отдельно взятому административному району города. Для моего исследования как раз интересны именно эти данные, по каждому из 22 отдельно взятому району Праги.
url_population = 'https://www.czso.cz/documents/10180/25233177/sldb_zv.csv'
df_population = pd.read_csv(url_population,encoding = "ISO 8859-2")
df_population = df_population[(df_population.uzcis == 44)& (df_population.nazev.str.find('Praha') != -1)][['nazev','u01','u04', 'u05', 'u06']]
df_population.rename(columns={'nazev':'Name','u01':'Total', 'u04':'Kids', 'u05':'Middle', 'u06':'Senior'}, inplace = True)
df_population['Name'] = df_population['Name'].map(lambda x: x.lower())| typuz_naz | nazev | uzcis | uzkod | u01 |
|---|---|---|---|---|
| kraj | Hlavni mesto Praha | 100 | 3018 | 1268796 |
Для визуализации данных я взял географические границы административных районов. Они доступны на портале IPR Praha.
Для удобства дальнейшего анализа я убрал лишние столбцы и свел данные с этих двух источников в единую таблицу, которую можно посмотреть на моем GitHub repository
| Name | Geometry | Area | Total | Kids | |
|---|---|---|---|---|---|
| 0 | praha 1 | [[14.410891049000043, 50.078674687000046], [14... | 5538443.86 | 30561.0 | 2391.0 |
| 1 | praha 10 | [[14.531321086000048, 50.072240288000046], [14... | 18599366.98 | 113200.0 | 12213.0 |
| 2 | praha 11 | [[14.54355294800007, 50.03618763800006], [14.5... | 9793679.84 | 75741.0 | 8688.0 |
Куда ходят наши дети?
В рамках данного исследования я решил сфокусироваться на наиболее часто посещаемых местах: школы, кружки, спортивные секции, игровые площадки и библиотеки. Данные были получены из различных источников и преобразованы в набор, содержащий нужную мне информацию: тип объекта, принадлежность к административному округу, координаты. Я сознательно не использовал какое-либо гео API, во-первых, из-за сильной ограниченности бесплатных версий, а также из-за того что не всегда можно быть уверенным в достоверности этих данных.
Вся актуальная информация по школам, а также другим образовательным учреждениям находится в свободном доступе на сайте министерства образования. XML файл содержит исчерпывающую информацию обо всех учреждениях, подчиняющихся министерству. По Праге это 2273 строки. К сожалению, описание к данному файлу отсутствовало, поэтому пришлось вытащить все возможные типы учреждений, их кодовые обозначения и самому понять, какие именно типы меня интересуют.
Отфильтровав лишние данные, я получил порядка 500 объектов. Также сразу убрал ненужную мне информацию, оставив только: тип учреждения, его адрес и районную принадлежность.
Для будущей модели мне не интересен фактический адрес объекта, поэтому с помощью geo-API я из адреса получил широту и долготу.
# Coordinates retrieve function
import geocoder
def get_coordinates(dataFrame, index_row):
dict_coordinates = {}
total_count = len(dataFrame.index)
current = 0
errors = 0
for index, row in dataFrame.iterrows():
try:
g = geocoder.arcgis(row[index_row])
lat = g.json['lat']
lng = g.json['lng']
dict_coordinates[index] = [lat, lng]
current+=1
except:
errors+=1
print ('Failed to get coordinates for {}: {}'.format(index_row, sys.exc_info()[0]))
dataFrame['latitude'] = 0.0
dataFrame['longitude'] = 0.0
for k, v in dict_coordinates.items():
dataFrame.loc[k,'latitude']=v[0]
dataFrame.loc[k,'longitude']=v[1]
print('Done: Total: {} Success: {} Error {}'.format(total_count, current, errors))
print('Environment was initializied')
url_schools = 'https://rejstriky.msmt.cz/opendata/vrejcz010.xml'
file_schools = 'schools.xml'
results = requests.get(url_schools)
results.content
with open(file_schools, 'w') as file:
file.write(results.text)
print('Loaded')
import xml.etree.ElementTree as et
xtree = et.parse(file_schools)
xroot = xtree.getroot()
dic_scools = []
try:
for entry in xroot.findall('PravniSubjekt'):
place_group = entry.find('SkolyZarizeni')
if(place_group is None):
continue
for place in place_group.findall('SkolaZarizeni'):
s_id = place.find('IZO').text
s_type = place.find('SkolaDruhTyp').text
s_name = place.find('SkolaPlnyNazev').text
s_capasity = place.find('SkolaKapacita').text
s_adress = place.find('SkolaMistaVykonuCinnosti')
s_actual_add = s_adress.find('SkolaMistoVykonuCinnosti')
s_addres1 = s_actual_add.find('MistoAdresa1').text
s_addres2 = s_actual_add.find('MistoAdresa2').text
s_addres3 = s_actual_add.find('MistoAdresa3').text
dic_scools.append([s_id, s_name, s_type, s_capasity, '{} {} {}'.format(s_addres1, s_addres2, s_addres3)])
print('Completed. Total schools and educational centers count: {}'.format(len(dic_scools)))
except:
print ('Exception', sys.exc_info()[0])
columns = ['id', 'name', 'type', 'capacity', 'address']
df_education = pd.DataFrame(dic_scools, columns = columns)
print('Dataframe created: {},{}'.format(df_education.shape[0], df_education.shape[1]))
#upload to datastore
df_prague.to_csv('prague_schools.csv')
upload_file(storage_creds,'prague_schools.csv','prague_schools.csv')
#Check for predefinied types at schools dataframe
types = df_education['type'].unique()
print('Types in XML file')
for t in types:
print(t,df_education[df_education.type == t].iloc[0,1])
#filtering types
with pd.option_context('mode.chained_assignment', None):
types = ['B00', 'F10', 'C00','H22', 'G11']
types_shu = types[0:3]
df_education_selected = df_education.loc[df_education.type.isin(types)]
df_education_selected.loc[df_education_selected['type'].isin(types_shu), 'Type'] = 'school'
df_education_selected = df_education_selected.fillna('educatioanal center')
print('Schools and educational centers count {}'.format(df_education_selected.shape[0]))
print('Unique types {}'.format(df_education_selected['Type'].unique()))
#Cleaning and retriving coordinates
df_education_selected.loc[0:, 'District_Name'] = df_education_selected.loc[0:,'address'].apply(lambda x: ' '.join(x.split()[-2:]).lower())
columns_to_drop = ['id','name','capacity', 'type']
df_education_selected.drop(columns = columns_to_drop, inplace = True)
get_coordinates(df_education_selected, 'address')
df_education_selected.drop(columns = ['address'], inplace= True)
df_education_selected.head()
| Type | District_Name | latitude | longitude |
|---|---|---|---|
| school | praha 4 | 50.008620 | 14.448992 |
| school | praha 1 | 50.080344 | 14.415264 |
Точно такие же шаги были сделаны для библиотек, спортивных центров и игровых площадок. Разница лишь заключалась в источниках данных и форматах.
Объединив всё в общую таблицу, я получил набор, содержащий 1623 строки. Скачать его можно также с моего GitHub Repository.
Граф улиц
Данные уличной сети я взял из OpenStreetMap. Дорожная сеть Праги представлена геометрическими линиями, характеризованными длиной. На основании этих данных на этапе моделирования будет построен граф маршрутной топологии, и по нему из каждого узла будет построен маршрут до интересующих нас точек.
#Loading data from previous steps
poi_file_name = files['poi']
population_file_name = files['districts']
df_prague_population, selected_pois = get_data(population_file_name, poi_file_name)
print('Total POIs to explore: {}'.format(len(selected_pois)))
print('Total Districts to explore: {}'.format(len(df_prague_population)))
#Buiding graph
start_time = time.time()
bbox = get_bounding_box(df_prague_population['Geometry'])
bbox_string = '_'.join([str(x) for x in bbox])
net_filename = 'network_{}.h5'.format(bbox_string)
print('Selected region bounding box is {}'.format(','.join([str(x) for x in bbox])) )
bbox_aspect_ratio = (bbox[2] - bbox[0]) / (bbox[3] - bbox[1])
print("Build new network")
network = osm.pdna_network_from_bbox(bbox[3], bbox[2], bbox[1], bbox[0],network_type='walk')
print ('Remove low-connectivity nodes and save to h5')
lcn = network.low_connectivity_nodes(impedance=1000, count=10, imp_name='distance')
network.save_hdf5(net_filename, rm_nodes=lcn)
upload_file(storage_creds,net_filename,net_filename)
print('Network with {:,} nodes builded in {:,.2f} secs'.format(len(network.node_ids), time.time()-start_time))
#Statistics
#Edge node pairs completed. Took 311.64 seconds
#Returning processed graph with 140,877 nodes and 204,649 edges...
#Completed OSM data download and Pandana node and edge table creation in 334.49 seconds
#Remove low-connectivity nodes and save to h5 File #network_14.224437012000067_49.94190007000003_14.706787572000053_50.17742967400005.h5 Uploaded
#Network with 140,877 nodes builded in 701.63 secsВ сумме пешеходная сеть Праги содержит 140 822 узла и 204 575 связей. B как видно постронение заняло примерно 10 минут. Готовая сеть лежит на GitHub. На этом этап сбора и очистки данных закончен. На выходе я получил 2 набора данных и уличную сеть Праги.
Более подробно изучить весь процесс а также посмотреть код можно в этом блокноте Data aquisition and cleaning
Анализ данных
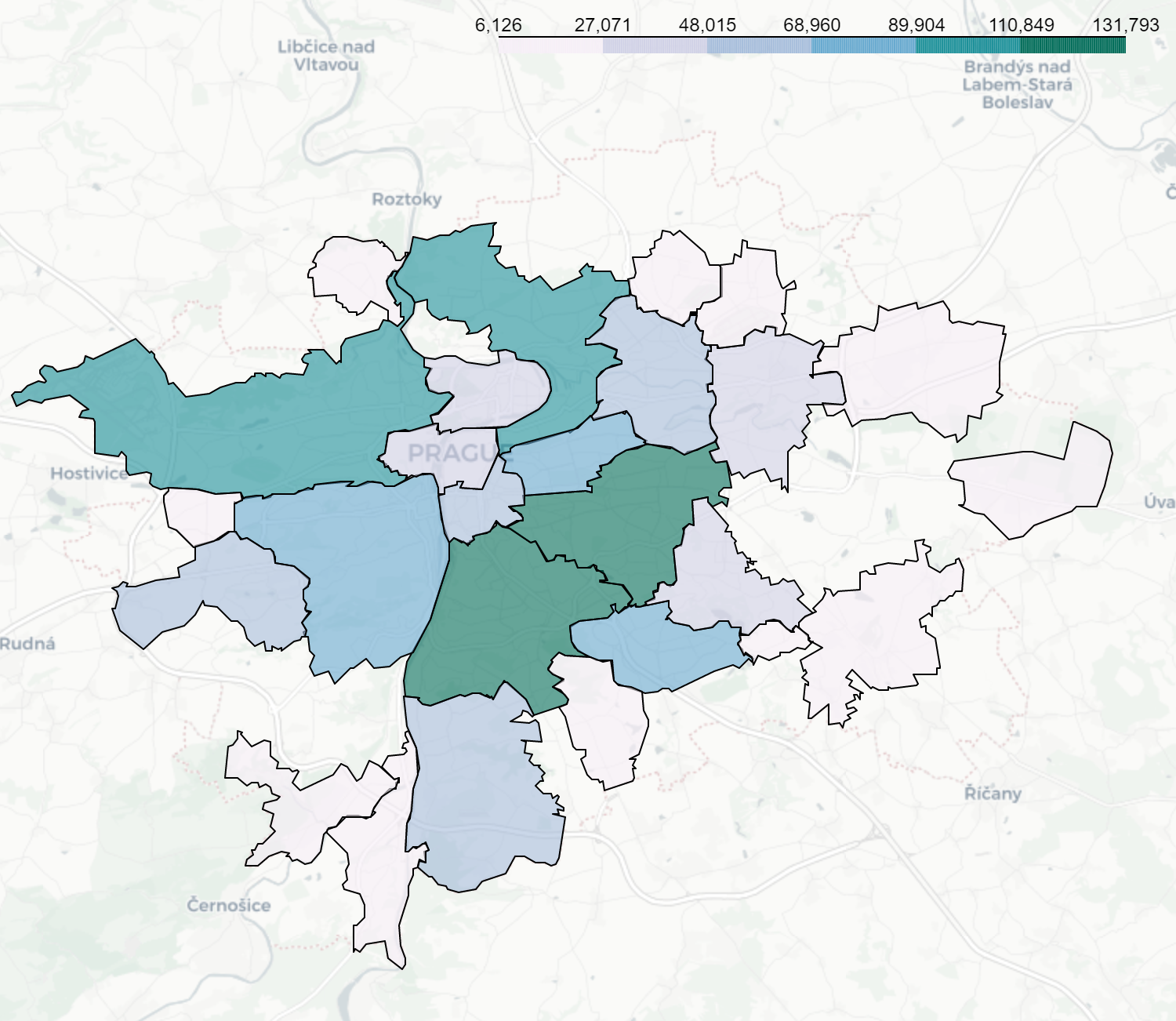
Общая численность населения Праги составляет около 1,3 миллиона человек. Самые высокие значения — в южных районах: от 110 тыс. до 130 тыс. Все районы с населением выше среднего расположены вокруг районов исторического центра. Средняя численность населения этих районов составляет 70 тыс. Это ожидаемо: большинство людей в таких городах, как Прага, живут как можно ближе к историческому центру, но не внутри него. Два крупнейших района на севере — с населением от 90 до 100 тыс. — говорят нам о том, в каком направлении происходит развитие Праги.
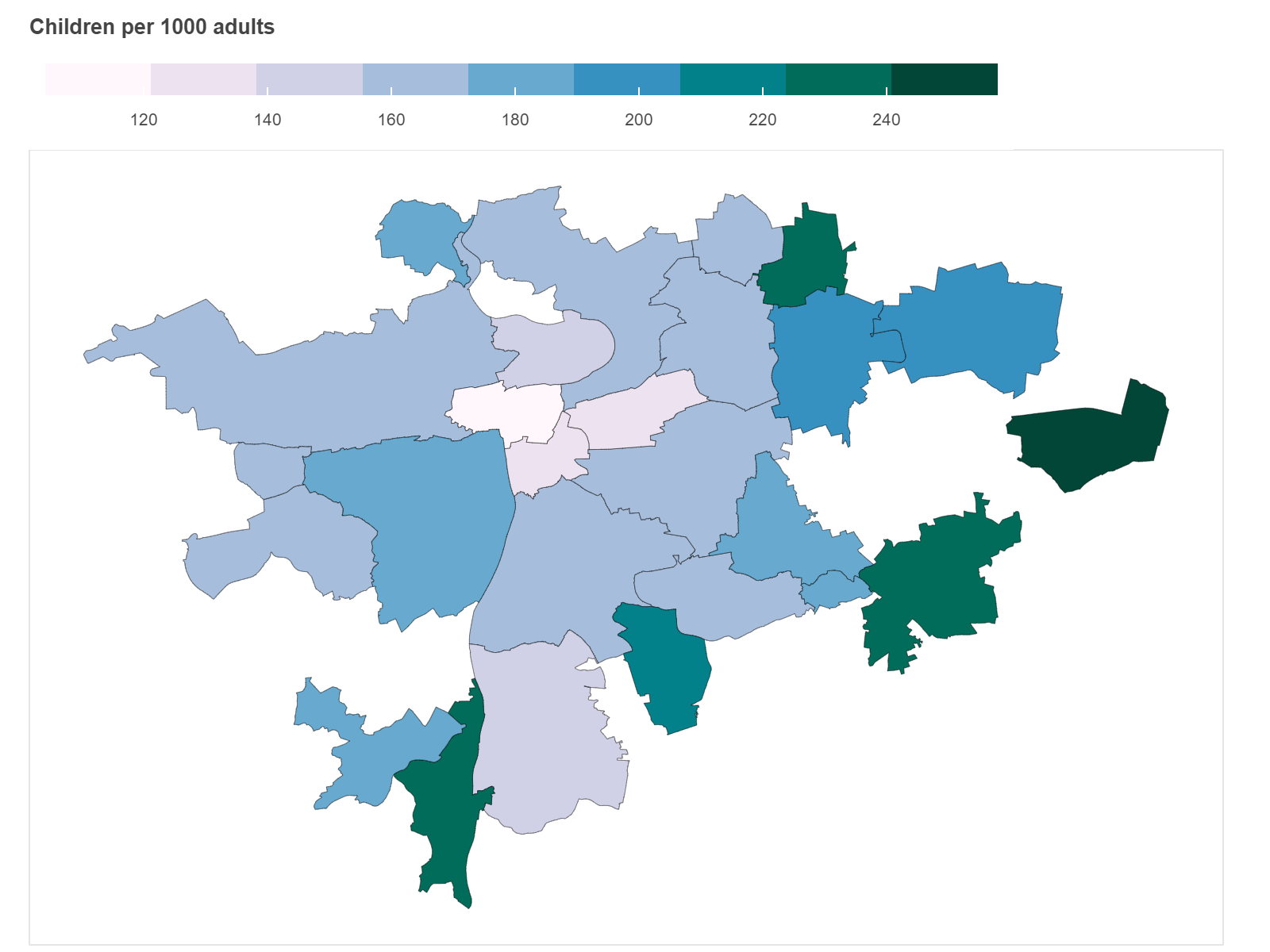
На следующей диаграмме мы ясно видим районы, которые в основном интересны семейным парам. Центральные районы и пригороды имеют самые низкие значения, в то время как районы вокруг центра, но не внутри него, имеют средние значения, примерно от 160 до 180 детей на 1000 взрослых.
Анализируя население Праги с точки зрения демографии, можно заметить, что распределение детей на 1000 взрослых соотносится с нашим представлением о районах города.
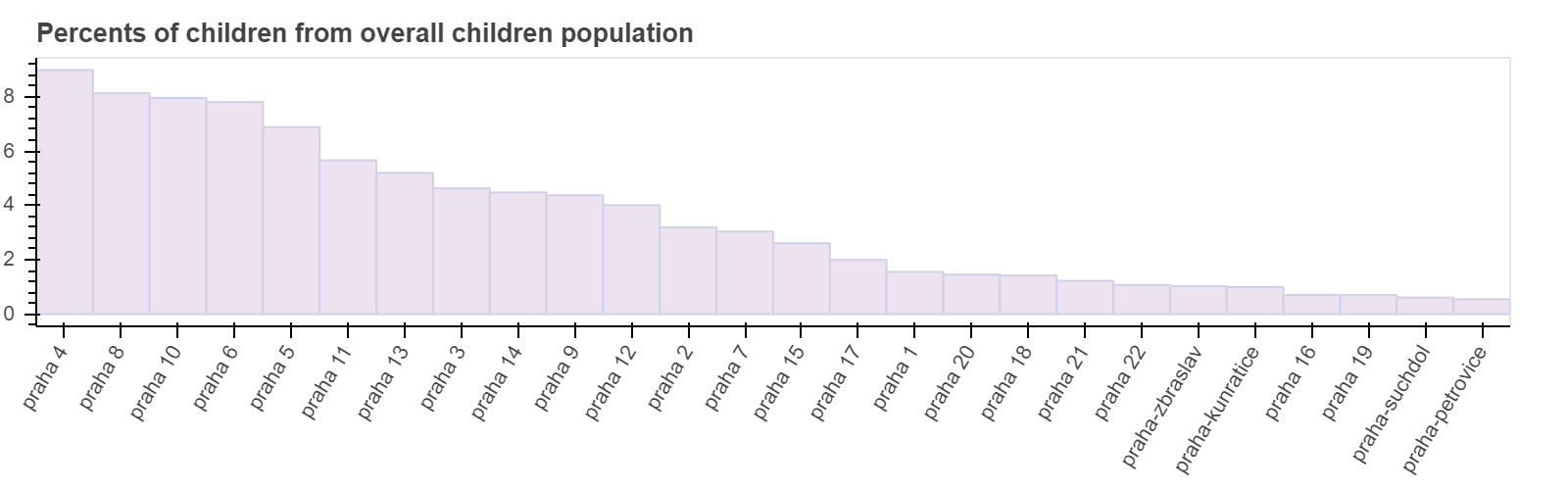
Топ-10 районов с наибольшим количеством детей повторяют топ районов из предыдущих графиков. Максимум у нас — это 8 процентов в Праге 4.
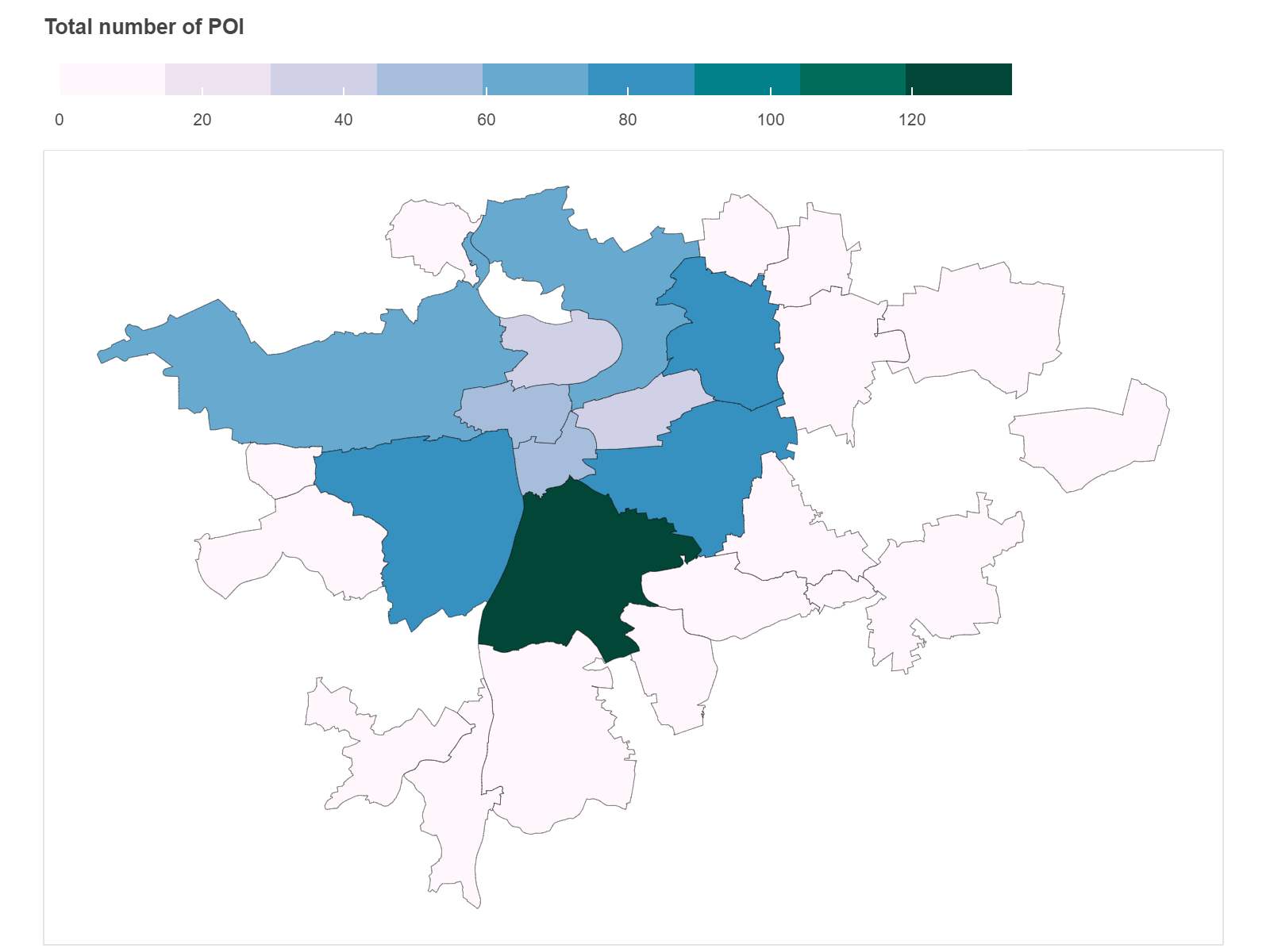
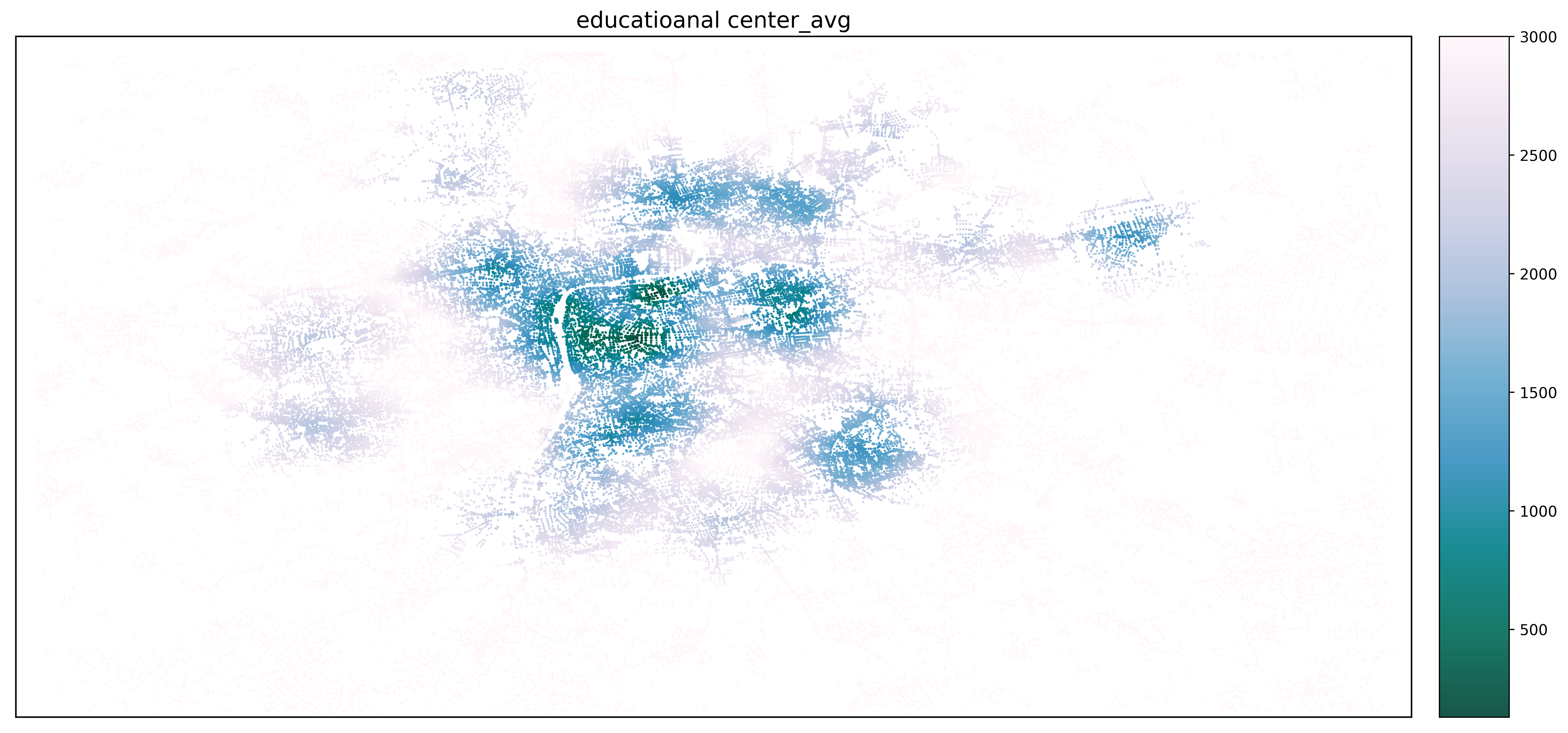
Выбранные нами объекты также сосредоточены вокруг исторического центра. Распределение по районам коррелирует с численностью населения районов. У нас примерно одинаковое количество точек во всех районах из топ-10 по численности населения, но с аномально высокими значениями на юге.
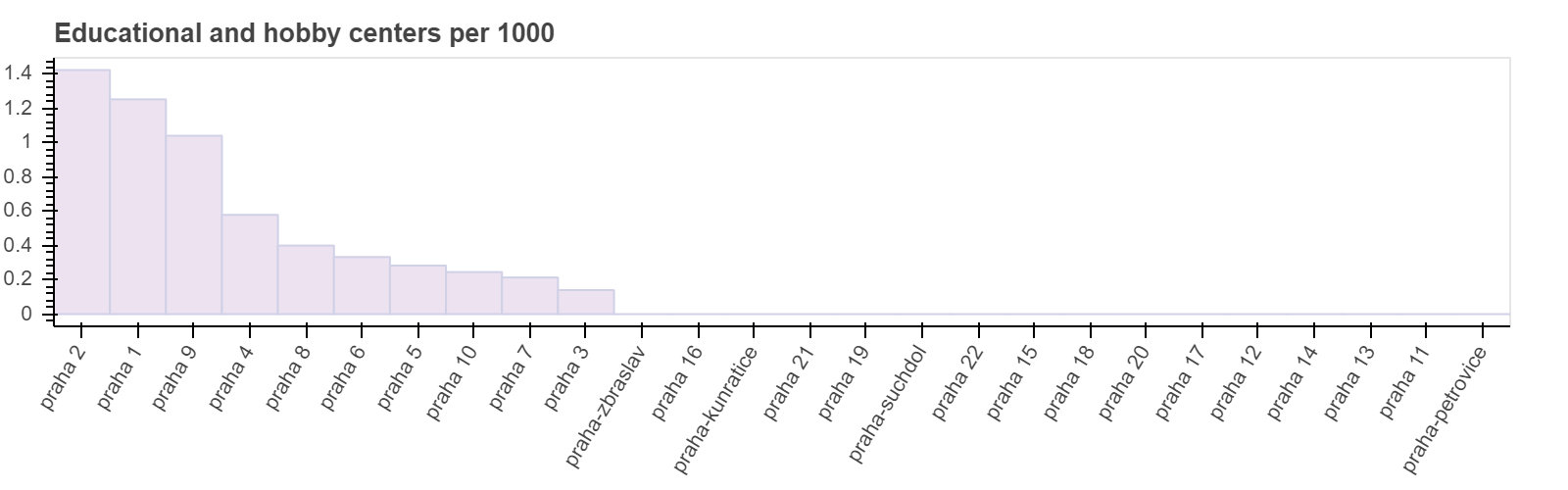
Общее количество объектов не дает нам полного представления о том, насколько хорош каждый отдельно взятый район для детей. Для нас интереснее посмотреть соотношение количества объектов к численности детей. Например, если мы посмотрим на гистограмму школ, мы заметим, что максимальные значения не коррелируют с величиной популяции. Прага 1 имеет самые высокие значения, но если мы посмотрим на предыдущие графики, то увидим, что по проценту детей Прага 1 даже не входит в топ-10. С другой стороны, Прага 4 имеет самые высокие значения населения, а также средние значения школ/1000. С одной стороны, это связано с низкой численностью детей в центре города, с другой стороны причины в том, что концентрация образовательных учреждений в центре города обычно выше.
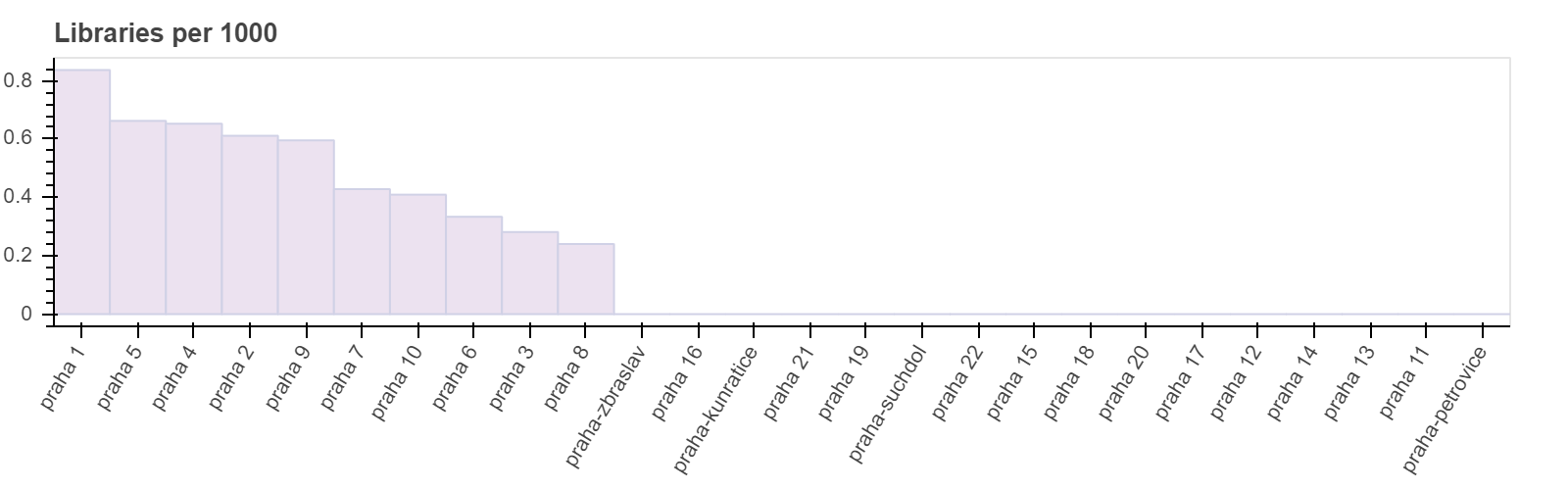
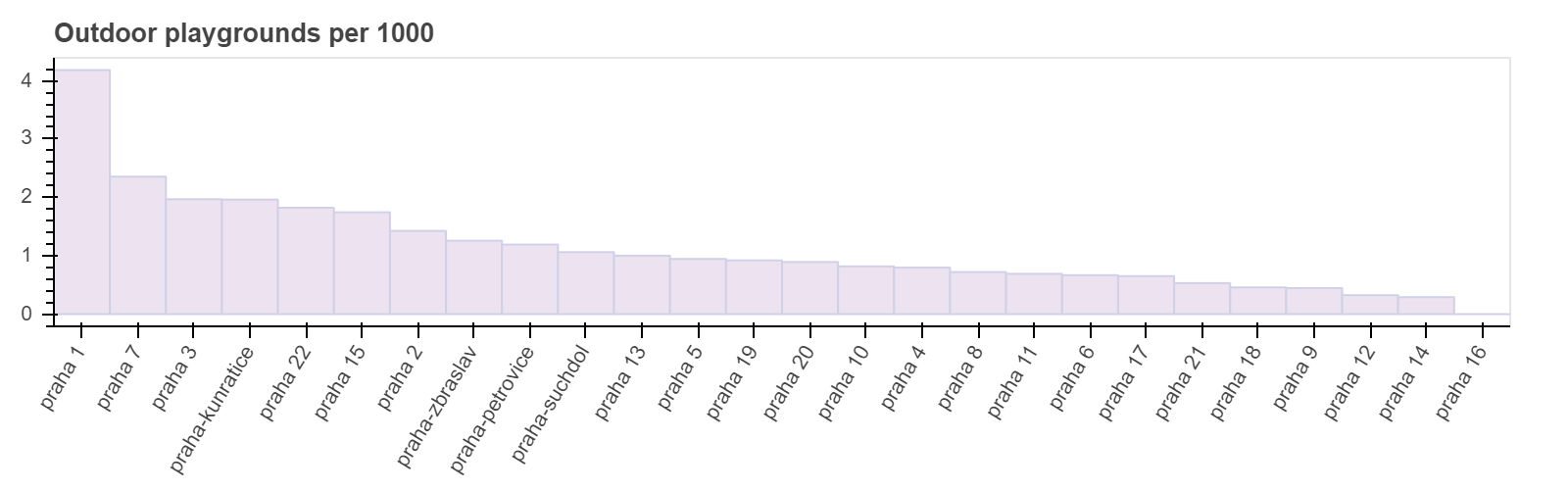
Такую же картину мы видим на следующих гистограммах. Центральные районы имеют самое высокое значение Объектов на 1000 детей, а пригороды — самое низкое.

Построение модели
Для нашего исследования мы не будем использовать четкие границы города, а возьмем квадратную область, описывающую реальные границы. (Мы не можем использовать меньший размер границ — например, административные или исторические районы — поскольку мы должны учитывать, что дети, проживающие на границах двух районов, могут посещать объекты в другом районе.)
На первом этапе мы преобразовали уличную сеть в граф. Для построения я использовал фреймворк Pandana. Огромный плюс этого фреймворка заключается в быстром выполнении статистической обработки данных по всей сети. В моем случае построение графа для 140 822 узлов с последующей очисткой заняло порядка 5 минут. (Под очисткой в данном случае я понимаю удаление точек, которые не представляют фактические пресечения и не являются узлами, исходя из теории графов.)
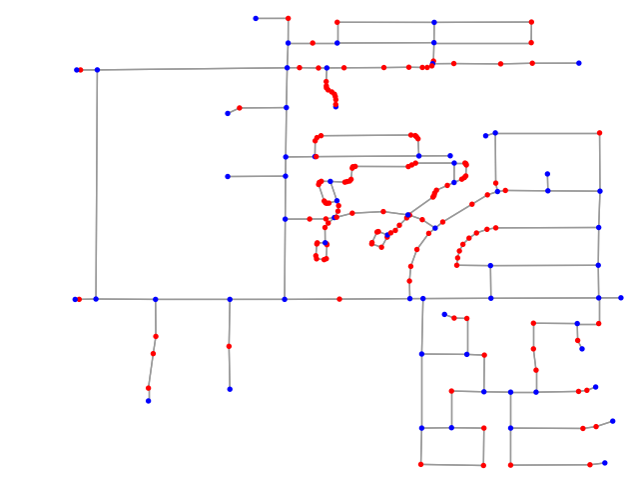
Вторым шагом мы накладываем наши объекты на граф и рассчитываем матрицы доступности. (Под матрицей доступности я считаю набор кратчайших расстояний из каждого узла графа до 3х объектов.) На следующем шаге полученные данные мы будем использовать для кластерного анализа
| id | 1_school | 2_school | 3_school | 1_educational center |
|---|---|---|---|---|
| 172508 | 218.384003 | 452.865997 | 502.253998 | 124.689003 |
| 172510 | 42.796001 | 326.665985 | 347.582001 | 50.898998 |
| 172512 | 226.128006 | 290.959991 | 300.862000 | 421.157990 |
| 172513 | 353.912994 | 393.170990 | 442.434998 | 627.351990 |
| 172514 | 270.234985 | 443.700989 | 492.393005 | 711.030029 |
Кластеризацию я выполнил методом k-средних. Это метод был изобретен в 1950-х годах математиком Гуго Штейнгаузом. Действие алгоритма таково, что он стремится минимизировать суммарное квадратичное отклонение точек кластеров от центров этих кластеров.
Алгоритм представляет собой версию EM-алгоритма, применяемого также для разделения смеси гауссиан. Он разбивает множество элементов векторного пространства на заранее известное число кластеров k.
Основная идея заключается в том, что на каждой итерации перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге. Затем векторы разбиваются на кластеры вновь, в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике.
Алгоритм завершается, когда на какой-то итерации не происходят изменения внутри кластерного расстояния. Это происходит за конечное число итераций, так как количество возможных разбиений итогового множества конечно, а на каждом шаге суммарное квадратичное отклонение уменьшается. Поэтому зацикливание невозможно.
Так как алгоритм предполагает заранее известное количество кластеров, я применил еще один хорошо известный алгоритм — Elbow. С его помощью можно определить оптимальное количество кластеров, и в результате я получил 4 кластера.
Заключительным шагом я рассчитал для каждого кластера среднее время, за которое ребенок может добраться пешком до ближайшего объекта, а также ввел понятие оценка доступности = фактическое расстояние /1300.
| Cluster No | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Walkability Score | 1.3 | 2.3 | 1.0 | 1.7 |
| Walking time (minutes) | ||||
| Schools | 9 | 44 | 6 | 19 |
| Hobby | 36 | 45 | 20 | 44 |
| Library | 30 | 45 | 23 | 44 |
| Sport facilities | 8 | 43 | 6 | 14 |
| Playgrounds | 45 | 45 | 45 | 45 |



Выводы
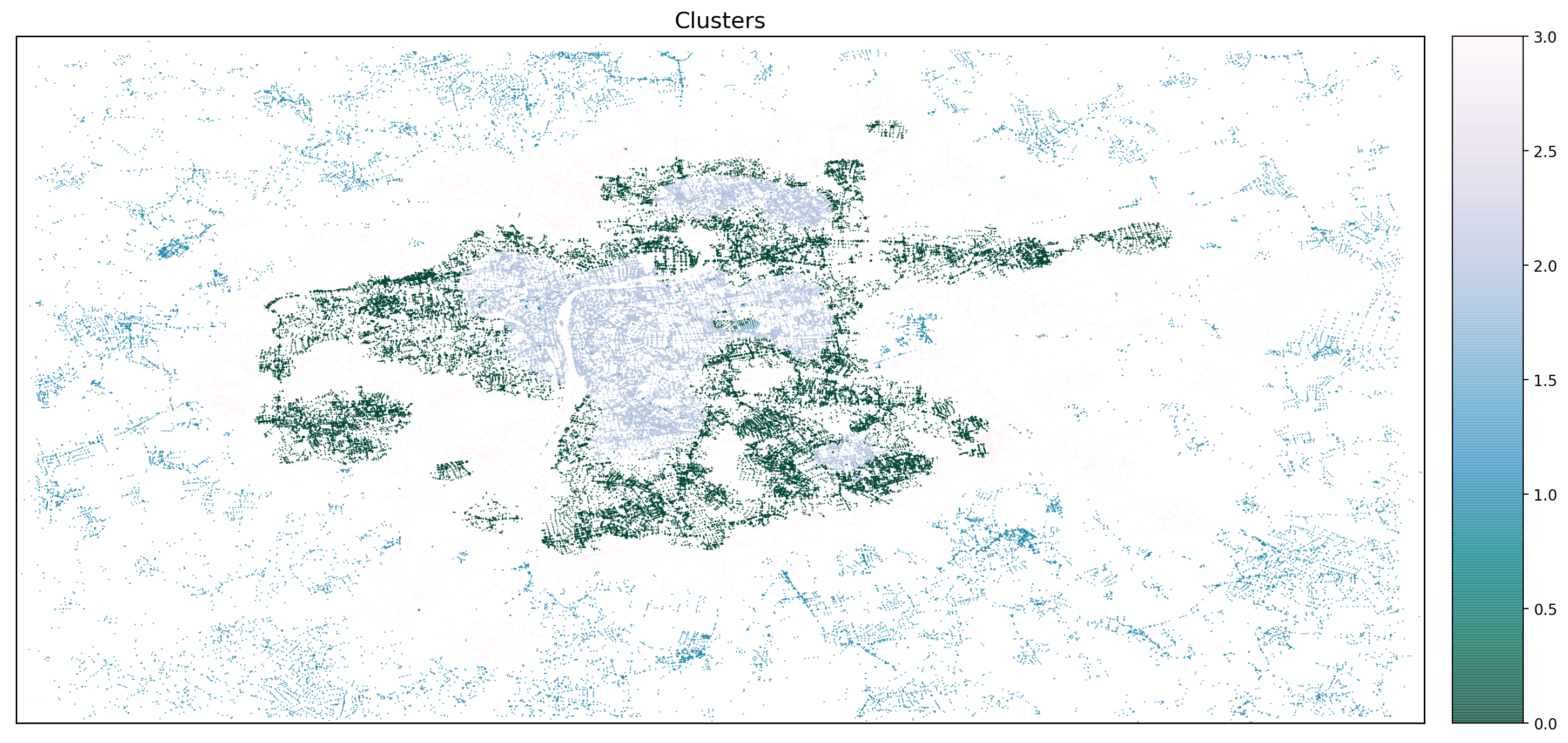
В результате мы имеем 4 кластера в Праге.
Кластер №2 имеет оптимальный показатель пешеходной доступности, равный единице. Это означает, что из каждой точки внутри этого кластера дети могут достичь всех необходимых объектов инфраструктуры примерно за 15 минут. Школы наиболее доступны внутри этого кластера, что является очень хорошим результатом.
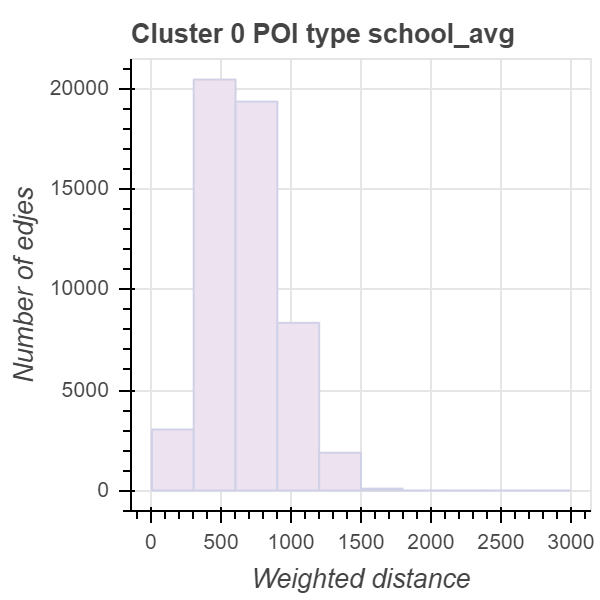
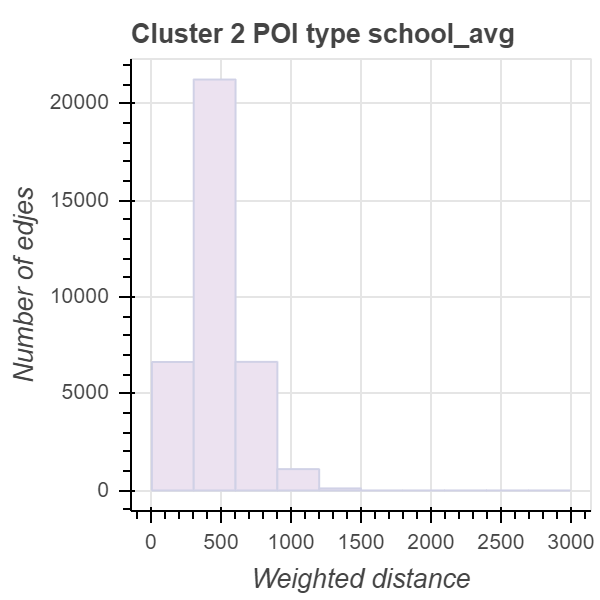
С другой стороны, кластер №2 охватывает в основном центральный исторический район, а мы знаем, что в этом районе численность детей ниже, чем в соседних районах.
Второй кластер — под номером 0 — имеет показатель пешеходной доступности около 1,3. Это означает, что до интересующих нас объектов этого кластера можно добраться менее чем за 10 минут. Это также очень хороший результат. Однако для обоих этих кластеров библиотеки и культурные центры имеют крайне низкие показатели — в среднем мы получаем порядка 30 минут ходьбы.


Заключение
В этом исследовании я проанализировал пешеходную доступность Праги для детей в возрасте 10-16 лет. Я определил основные места посещения для выбранной фокус-группы и выполнил измерение кратчайших расстояний до всех выбранных точек. С помощью алгоритма кластеризации я разделил исследуемую область на 4 кластера.
В будущих исследованиях я планирую провести более детальный анализ каждого типа. Также, хочется добавить веса к моему графу улиц, что бы при построении маршрута также учитывать рельеф. Также мне как родителю интересно посмотреть на пешеходную доступность не только с точки зрения кратчайших маршрутов, но и с точки зрения самых безопасных.
Ссылки
- Living Streets (The Pedestrians’ Association) A LIVING STREETS REPORT
- Criterion distances and correlates of active transportation to school in Belgian older adolescents. Delfien Van Dyck, Ilse De Bourdeaudhuij, Greet Cardon & Benedicte Deforche
- Naumann, S., & Kovalyov, M. Y. (2017). Pedestrian route search based on OpenStreetMap. In Intelligent Transport Systems and Travel Behaviour (pp. 87-96). Cham: Springer.
- Pandana
- THE MECHANICS OF WALKING IN CHILDREN
- OSMnx: Python for Street Networks
- География Праги
- Демография
- Образование и учебные заведения
- Библиотеки Праги: Wikipedia
- Спортивные учереждения: Opendata Prague
- Игровые и спортивные площадки: Opendata Prague


sshikov
А можно немножно подробнее про дорожную сеть? Скажем, есть такие улицы, по которым пешком и на велосипеде передвигаться нельзя, они только для транспорта. Кроме того, пересечение этих улиц тоже та еще эпопея — так что для вашей задачи нужно будет строить маршрут с учетом наличия переходов через такие улицы — потому что точка прямо на противоположной стороне улицы на самом деле может быть очень далеко на пешеходном маршруте (до перехода, через улицу, от перехода). Ну, или на месте таких улиц могут быть реки с мостами, если угодно, или железная дорога.
В итоге, напрашивается немного другой алгоритм: для всех POI, которые у нас являются точками, построить эквидистанты для пешеходов, причем как по равному расстоянию, так и по времени, а затем строить что-то типа пересечения этих областей.