В этой статье речь будет идти о исследовании зависимости между признаками, или как больше нравится — случайными величинами, переменными. В частности, мы разберем как ввести меру зависимости между признаками, используя критерий Хи-квадрат и сравним её с коэффициентом корреляции.
Для чего это может понадобиться? К примеру, для того, чтобы понять какие признаки сильнее зависимы от целевой переменной при построении кредитного скоринга — определении вероятности дефолта клиента. Или, как в моем случае, понять какие показатели нобходимо использовать для программирования торгового робота.
Отдельно отмечу, что для анализа данных я использую язык c#. Возможно это все уже реализовано на R или Python, но использование c# для меня позволяет детально разобраться в теме, более того это мой любимый язык программирования.
Начнем с совсем простого примера, создадим в экселе четыре колонки, используя генератор случайных чисел:
X =СЛУЧМЕЖДУ(-100;100)
Y =X*10+20
Z =X*X
T =СЛУЧМЕЖДУ(-100;100)

Как видно, переменная Y линейно зависима от X; переменная Z квадратично зависима от X; переменные X и Т независимы. Такой выбор я сделал специально, потому что нашу меру зависимости мы будем сравнивать с коэффициентом корреляции. Как известно, между двумя случайными величинами он равен по модулю 1 если между ними самый «жесткий» вид зависимости — линейный. Между двумя независимыми случайными величинами корреляция нулевая, но из равенства коэффициента корреляции нулю не следует независимость. Далее мы это увидим на примере переменных X и Z.
Сохраняем файл как data.csv и начинаем первые прикиди. Для начала рассчитаем коэффициент корреляции между величинами. Код в статью я вставлять не стал, он есть на моем github. Получаем корреляцию по всевозможным парам:
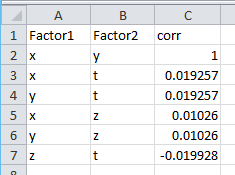
Видно, что у линейно зависимых X и Y коэффициент корреляции равен 1. А вот у X и Z он равен 0.01, хотя зависимость мы задали явную Z=X*X. Ясно, что нам нужна мера, которая «чувствует» зависимость лучше. Но прежде, чем переходить к критерию Хи-квадрат, давайте рассмотрим что такое матрица сопряженности.
Чтобы построить матрицу сопряженности мы разобьём диапазон значений переменных на интервалы (или категорируем). Есть много способов такого разбиения, при этом какого-то универсального не существует. Некоторые из них разбивают на интервалы так, чтобы в них попадало одинаковое количество переменных, другие разбивают на равные по длине интервалы. Мне лично по духу комбинировать эти подходы. Я решил воспользоваться таким способом: из переменной я вычитаю оценку мат. ожидания, потом полученное делю на оценку стандартного отклонения. Иными словами я центрирую и нормирую случайную величину. Полученное значение умножается на коэффициент (в этом примере он равен 1), после чего все округляется до целого. На выходе получается переменная типа int, являющаяся идентификатором класса.
Итак, возьмем наши признаки X и Z, категорируем описанным выше способом, после чего посчитаем количество и вероятности появления каждого класса и вероятности появления пар признаков:
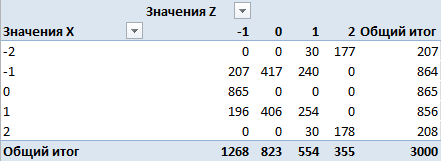
Это матрица по количеству. Здесь в строках — количества появлений классов переменной X, в столбцах — количества появлений классов переменной Z, в клетках — количества появлений пар классов одновременно. К примеру, класс 0 встретился 865 раз для переменной X, 823 раза для переменной Z и ни разу не было пары (0,0). Перейдем к вероятностям, поделив все значения на 3000 (общее число наблюдений):
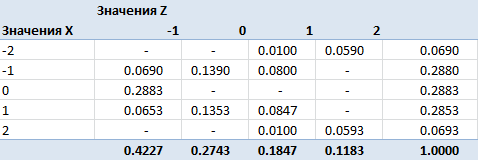
Получили матрицу сопряженности, полученную после категорирования признаков. Теперь пора задуматься над критерием. По определению, случайные величины независимы, если независимы сигма-алгебры, порожденные этими случайными величинами. Независимость сигма-алгебр подразумевает попарную независимость событий из них. Два события называются независимыми, если вероятность их совместного появления равна произведению вероятностей этих событий: Pij = Pi*Pj. Именно этой формулой мы будем пользоваться для построения критерия.
Нулевая гипотеза: категорированные признаки X и Z независимы. Эквивалентная ей: распределение матрицы сопряженности задается исключительно вероятностями появления классов переменных (вероятности строк и столбцов). Или так: ячейки матрицы находятся произведением соответствующих вероятностей строк и столбцов. Эту формулировку нулевой гипотезы мы будем использовать для построения решающего правила: существенное расхождение между Pij и Pi*Pj будет являться основанием для отклонения нулевой гипотезы.
Пусть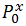 — вероятность появления класса 0 у переменной X. Всего у нас n классов у X и m классов у Z. Получается, чтобы задать распределение матрицы нам нужно знать эти n и m вероятностей. Но на самом деле если мы знаем n-1 вероятность для X, то последняя находится вычитанием из 1 суммы других. Таким образом для нахождения распределения матрицы сопряженности нам надо знать l=(n-1)+(m-1) значений. Или мы имеем l-мерное параметрическое пространство, вектор из которого задает нам наше искомое распределение. Статистика Хи-квадрат будет иметь следующий вид:
— вероятность появления класса 0 у переменной X. Всего у нас n классов у X и m классов у Z. Получается, чтобы задать распределение матрицы нам нужно знать эти n и m вероятностей. Но на самом деле если мы знаем n-1 вероятность для X, то последняя находится вычитанием из 1 суммы других. Таким образом для нахождения распределения матрицы сопряженности нам надо знать l=(n-1)+(m-1) значений. Или мы имеем l-мерное параметрическое пространство, вектор из которого задает нам наше искомое распределение. Статистика Хи-квадрат будет иметь следующий вид:
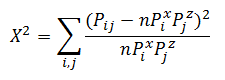
и, согласно теореме Фишера, иметь распределение Хи-квадрат с n*m-l-1=(n-1)(m-1) степенями свободы.
Зададимся уровнем значимости 0.95 (или вероятность ошибки первого рода равна 0.05). Найдем квантиль распределения Хи квадрат для данного уровня значимости и степеней свободы из примера (n-1)(m-1)=4*3=12: 21.02606982. Сама статистика Хи-квадрат для переменных X и Z равна 4088.006631. Видно, что гипотеза о независимости не принимается. Удобно рассматривать отношение статистики Хи-квадрат к пороговому значению — в данном случае оно равно Chi2Coeff=194.4256186. Если это отношение меньше 1, то гипотеза о независимости принимается, если больше, то нет. Найдем это отношение для всех пар признаков:
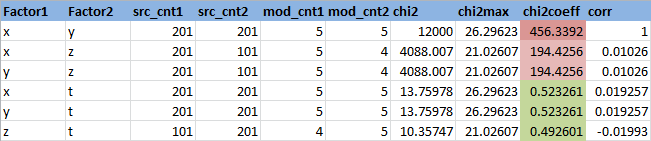
Здесь Factor1 и Factor2 — имена признаков
src_cnt1 и src_cnt2 — количество уникальных значений исходных признаков
mod_cnt1 и mod_cnt2 — количество уникальных значений признаков после категорирования
chi2 — статистика Хи-квадрат
chi2max — пороговое значение статистики Хи-квадрат для уровня значимости 0.95
chi2Coeff — отношение статистики Хи-квадрат к пороговому значению
corr — коэффициент корреляции
Видно, что независимы (chi2coeff<1) получились следующие пары признаков — (X,T), (Y,T) и (Z,T), что логично, так как переменная T генерируется случайно. Переменные X и Z зависимы, но менее, чем линейно зависимые X и Y, что тоже логично.
Код утилиты, рассчитывающей данные показатели я выложил на github, там же файл data.csv. Утилита принимает на вход csv-файл и высчитывает зависимости между всеми парами колонок: PtProject.Dependency.exe data.csv
Ссылки:
1. Проверка гипотезы независимости: критерий хи-квадрат Пирсона
2. Критерий Хи-квадрат Пирсона для проверки параметрической гипотезы
3. Реализация критерия на c#
Для чего это может понадобиться? К примеру, для того, чтобы понять какие признаки сильнее зависимы от целевой переменной при построении кредитного скоринга — определении вероятности дефолта клиента. Или, как в моем случае, понять какие показатели нобходимо использовать для программирования торгового робота.
Отдельно отмечу, что для анализа данных я использую язык c#. Возможно это все уже реализовано на R или Python, но использование c# для меня позволяет детально разобраться в теме, более того это мой любимый язык программирования.
Начнем с совсем простого примера, создадим в экселе четыре колонки, используя генератор случайных чисел:
X =СЛУЧМЕЖДУ(-100;100)
Y =X*10+20
Z =X*X
T =СЛУЧМЕЖДУ(-100;100)

Как видно, переменная Y линейно зависима от X; переменная Z квадратично зависима от X; переменные X и Т независимы. Такой выбор я сделал специально, потому что нашу меру зависимости мы будем сравнивать с коэффициентом корреляции. Как известно, между двумя случайными величинами он равен по модулю 1 если между ними самый «жесткий» вид зависимости — линейный. Между двумя независимыми случайными величинами корреляция нулевая, но из равенства коэффициента корреляции нулю не следует независимость. Далее мы это увидим на примере переменных X и Z.
Сохраняем файл как data.csv и начинаем первые прикиди. Для начала рассчитаем коэффициент корреляции между величинами. Код в статью я вставлять не стал, он есть на моем github. Получаем корреляцию по всевозможным парам:

Видно, что у линейно зависимых X и Y коэффициент корреляции равен 1. А вот у X и Z он равен 0.01, хотя зависимость мы задали явную Z=X*X. Ясно, что нам нужна мера, которая «чувствует» зависимость лучше. Но прежде, чем переходить к критерию Хи-квадрат, давайте рассмотрим что такое матрица сопряженности.
Чтобы построить матрицу сопряженности мы разобьём диапазон значений переменных на интервалы (или категорируем). Есть много способов такого разбиения, при этом какого-то универсального не существует. Некоторые из них разбивают на интервалы так, чтобы в них попадало одинаковое количество переменных, другие разбивают на равные по длине интервалы. Мне лично по духу комбинировать эти подходы. Я решил воспользоваться таким способом: из переменной я вычитаю оценку мат. ожидания, потом полученное делю на оценку стандартного отклонения. Иными словами я центрирую и нормирую случайную величину. Полученное значение умножается на коэффициент (в этом примере он равен 1), после чего все округляется до целого. На выходе получается переменная типа int, являющаяся идентификатором класса.
Итак, возьмем наши признаки X и Z, категорируем описанным выше способом, после чего посчитаем количество и вероятности появления каждого класса и вероятности появления пар признаков:

Это матрица по количеству. Здесь в строках — количества появлений классов переменной X, в столбцах — количества появлений классов переменной Z, в клетках — количества появлений пар классов одновременно. К примеру, класс 0 встретился 865 раз для переменной X, 823 раза для переменной Z и ни разу не было пары (0,0). Перейдем к вероятностям, поделив все значения на 3000 (общее число наблюдений):

Получили матрицу сопряженности, полученную после категорирования признаков. Теперь пора задуматься над критерием. По определению, случайные величины независимы, если независимы сигма-алгебры, порожденные этими случайными величинами. Независимость сигма-алгебр подразумевает попарную независимость событий из них. Два события называются независимыми, если вероятность их совместного появления равна произведению вероятностей этих событий: Pij = Pi*Pj. Именно этой формулой мы будем пользоваться для построения критерия.
Нулевая гипотеза: категорированные признаки X и Z независимы. Эквивалентная ей: распределение матрицы сопряженности задается исключительно вероятностями появления классов переменных (вероятности строк и столбцов). Или так: ячейки матрицы находятся произведением соответствующих вероятностей строк и столбцов. Эту формулировку нулевой гипотезы мы будем использовать для построения решающего правила: существенное расхождение между Pij и Pi*Pj будет являться основанием для отклонения нулевой гипотезы.
Пусть
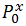 — вероятность появления класса 0 у переменной X. Всего у нас n классов у X и m классов у Z. Получается, чтобы задать распределение матрицы нам нужно знать эти n и m вероятностей. Но на самом деле если мы знаем n-1 вероятность для X, то последняя находится вычитанием из 1 суммы других. Таким образом для нахождения распределения матрицы сопряженности нам надо знать l=(n-1)+(m-1) значений. Или мы имеем l-мерное параметрическое пространство, вектор из которого задает нам наше искомое распределение. Статистика Хи-квадрат будет иметь следующий вид:
— вероятность появления класса 0 у переменной X. Всего у нас n классов у X и m классов у Z. Получается, чтобы задать распределение матрицы нам нужно знать эти n и m вероятностей. Но на самом деле если мы знаем n-1 вероятность для X, то последняя находится вычитанием из 1 суммы других. Таким образом для нахождения распределения матрицы сопряженности нам надо знать l=(n-1)+(m-1) значений. Или мы имеем l-мерное параметрическое пространство, вектор из которого задает нам наше искомое распределение. Статистика Хи-квадрат будет иметь следующий вид: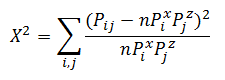
и, согласно теореме Фишера, иметь распределение Хи-квадрат с n*m-l-1=(n-1)(m-1) степенями свободы.
Зададимся уровнем значимости 0.95 (или вероятность ошибки первого рода равна 0.05). Найдем квантиль распределения Хи квадрат для данного уровня значимости и степеней свободы из примера (n-1)(m-1)=4*3=12: 21.02606982. Сама статистика Хи-квадрат для переменных X и Z равна 4088.006631. Видно, что гипотеза о независимости не принимается. Удобно рассматривать отношение статистики Хи-квадрат к пороговому значению — в данном случае оно равно Chi2Coeff=194.4256186. Если это отношение меньше 1, то гипотеза о независимости принимается, если больше, то нет. Найдем это отношение для всех пар признаков:

Здесь Factor1 и Factor2 — имена признаков
src_cnt1 и src_cnt2 — количество уникальных значений исходных признаков
mod_cnt1 и mod_cnt2 — количество уникальных значений признаков после категорирования
chi2 — статистика Хи-квадрат
chi2max — пороговое значение статистики Хи-квадрат для уровня значимости 0.95
chi2Coeff — отношение статистики Хи-квадрат к пороговому значению
corr — коэффициент корреляции
Видно, что независимы (chi2coeff<1) получились следующие пары признаков — (X,T), (Y,T) и (Z,T), что логично, так как переменная T генерируется случайно. Переменные X и Z зависимы, но менее, чем линейно зависимые X и Y, что тоже логично.
Код утилиты, рассчитывающей данные показатели я выложил на github, там же файл data.csv. Утилита принимает на вход csv-файл и высчитывает зависимости между всеми парами колонок: PtProject.Dependency.exe data.csv
Ссылки:
1. Проверка гипотезы независимости: критерий хи-квадрат Пирсона
2. Критерий Хи-квадрат Пирсона для проверки параметрической гипотезы
3. Реализация критерия на c#
Комментарии (4)

DreamWalker
17.08.2015 15:53А вы смотрели ChiSquareTest из Accord.NET Framework?

sdev
17.08.2015 16:01Спасибо за ссылку, библиотека интересная.
ChiSquareTest — немного не то, про что я писал.
У нее такой интефейс: ChiSquareTest(expected, observed, degreesOfFreedom);
Т.е. она применяется, когда expected и observed уже посчитаны и известно degreesOfFreedom. В терминах задачи это expected=Pij, observed=Pi*Pj, degreesOfFreedom=(n-1)*(m-1).
Задача, в основном, и заключается в том, чтобы понять где здесь Хи-квадрат, о чем я и писал. В начале у нас нет никаких expected и observed, есть только значения признаков, которые могут быть совершенно разными.


bougakov
Вы фигово объясняете применение этого теста, вы уж простите. Собственно, у вас две строчки про то, как он будет использоваться, а потом — много сухого текста из учебника, пичаль.
Я вот вполуха слушал про chi-square на первому курсе и пользовался им механически. А смысл дошёл, когда рассказали про сенсорный тест «треугольником»:
Мы даём испытуемому три образца тестируемого продукта, из которых два одинаковы, а третий — отличается. Например, мы попробовали сменить поставщика какого-то ингредиента и боимся, что покупатели заметят разницу и перестанут покупать.
У испытуемого шанс определить отличающийся образец наугад — одна треть. После повторения эксперимента на десятке людей мы получаем долю верно угаданных образцов, которая больше или меньше 1/3 — и как раз используем chi square для того, чтобы понять, значимо ли отличие, или нет.
Так понятнее, не правда ли?
P.S. А чем вам встроенная в Эксель функция CHITEST не угодила?
sdev
Скажу честно про CHITEST я до этого не слышал.
Но у меня сильные сомнения, что её можно в этой задаче успешно применять, потому что:
1. Как-то категорировать переменные все равно придется.
2. Высчитывать пороговое значение тоже, видимо, придется (в параметрах у нее его нет)
3. Точно придется высчитывать разницу между Pij и Pi*Pj
В итоге, с моей точки зрения, еще больше мороки.
Плюс ко всему, акцент был сделан на том, что это c#-реализация, которая в дальнейшем будет использоваться в другом коде на c#.