Создать бесшовное изображение в Photoshop легко: обрезать изображение, взять обрезанную правую и нижнюю части, а потом приклеить их слева и сверху при помощи инструмента «Ослабить» (Fade). Но для правильной реализации бесшовных карт шума придётся хорошенько подумать.
Если у вас есть базовое представление о шуме Перлина, то вы знаете, что он состоит из интерполированных случайных чисел. В основном он используется в двух измерениях. Но также он полезен и в одном измерении (например, при движении), в трёх измерениях (цилиндрическое и сферическое преображение 3D-объектов), и даже в четырёх или пяти измерениях.
Можно использовать четырёхмерный шум для создания бесшовного 2D-изображения. Думать в четырёх измерениях нам не очень привычно, поэтому мы будем брать по одному измерению за раз.
В своих примерах я использовал симплекс-шум с двумя октавами. Симплекс-шум быстрее в больших размерностях, а благодаря своей треугольной природе он выглядит лучше.
Я написал небольшую функцию
drawNoise для создания холста и обработки в цикле массива пикселей.Одномерный бесшовный шум
В одном измерении шум является бесконечной плавной линией (моя реализация шума начинается с двух, поэтому я использую в качестве второго параметра константу). Здесь мы видим, что это просто интерполированные случайные числа.
// one dimensional line
fNoiseScale = .02;
drawNoise(function(i,x,y){
var v = Simplex.noise(
123+x*fNoiseScale
,137 // we just need one dimension so this parameter is a constant
);
return v*iSize>y?255:0;
}).img();
Одномерный шум
Можно использовать это в анимации, каждую миллисекунду пересчитывая значение шума, но также можно создать зацикленность и вычислить все значения заранее. Значения в показанном выше изображении не зацикливаются по краям. Но реализовать повторяемость довольно просто, для этого достаточно ещё одного измерения и петли… или круга.
Одномерная петля
Для большинства из вас шум Перлина выглядит примерно так, как показано на изображении ниже.

Если бы мы нарисовали здесь круг и считали значения шума на этом круге, то получили одномерную петлю.

Шум с окружностью для создания одномерной петли.
В коде это выглядит так:
// one dimensional loop
drawNoise(function(i,x,y){
var fNX = x/iSize // we let the x-offset define the circle
,fRdx = fNX*2*Math.PI // a full circle is two pi radians
,a = fRdsSin*Math.sin(fRdx)
,b = fRdsSin*Math.cos(fRdx)
,v = Simplex.noise(
123+a*fNoiseScale
,132+b*fNoiseScale
)
;
return v*iSize>y?255:0;
}).img().div(2);
Вероятно, вы уже поняли, к чему мы идём. Для зацикливания двухмерного изображения нам потребуется трёхмерная (как минимум) карта шума.
Цилиндрическая карта
Шум Перлина изначально был создан для непрерывного 3D-текстурирования (фильм «Трон»). Карта изображения не является листом бумаги, обёрнутым вокруг объекта, а вычисляется по расположению в трёхмерном поле шума. Поэтому при разрезании объекта мы всё равно сможем вычислить карту для новой созданной поверхности.
Прежде чем достичь нашей конечной цели — бесшовного изображения, мы сначала создадим изображение, бесшовно соединяемое слева и справа. Это похоже на двухмерную окружность для одномерной петли, но с одним дополнительным измерением: цилиндром.
// three dimensional cylindrical map
drawNoise(function(i,x,y){
var fNX = x/iSize
,fRdx = fNX*2*Math.PI
,a = fRdsSin*Math.sin(fRdx)
,b = fRdsSin*Math.cos(fRdx)
,v = Simplex.noise(
123+a*fNoiseScale
,132+b*fNoiseScale
,312+y*fNoiseScale // similar to the one dimensional loop but we add a third dimension defined by the image y-offset
)
;
return v*255<<0;
}).img().div(2);
Цилиндрическая карта шума
Сферическая карта изображения
Вы можете подумать, что для создания бесшовного изображения будет удобно использовать сферу, но вы ошибаетесь.
Я сделаю небольшое отступление и покажу, как вычисляется сферическая карта изображения и на что она похожа.
// three dimensional spherical map
document.body.addChild('h2').innerText = 'three dimensional spherical map';
fNoiseScale = .1;
var oSpherical = drawNoise(function(i,x,y){
var fNX = (x+.5)/iSize // added half a pixel to get the center of the pixel instead of the top-left
,fNY = (y+.5)/iSize
,fRdx = fNX*2*Math.PI
,fRdy = fNY*Math.PI // the vertical offset of a 3D sphere spans only half a circle, so that is one Pi radians
,fYSin = Math.sin(fRdy+Math.PI) // a 3D sphere can be seen as a bunch of cicles stacked onto each other, the radius of each of these is defined by the vertical position (again one Pi radians)
,a = fRdsSin*Math.sin(fRdx)*fYSin
,b = fRdsSin*Math.cos(fRdx)*fYSin
,c = fRdsSin*Math.cos(fRdy)
,v = Simplex.noise(
123+a*fNoiseScale
,132+b*fNoiseScale
,312+c*fNoiseScale
)
;
return v*255<<0;
}).img();
Сферическая карта шума

Сфера с шумом
Кубическая панорамная карта
Созданную нами сферу также можно использовать как панораму, если разместить в центре сферы камеру. Но лучшим способом будет применение кубической панорамы, потому что она имеет гораздо меньше граней. Сфера проецируется на шесть сторон куба, как показано на этом эскизе.

Наложение сферы на куб
Для каждого пикселя на поверхности куба нам нужно вычислить пересечение между точкой обзора C в центре и сферой. Это может показаться сложным, но на самом деле всё довольно просто.
Мы можем рассматривать линию CA как вектор. А векторы можно нормализировать, чтобы их направление не менялось, но длина при этом снижалась до 1. Благодаря этому все векторы вместе будут выглядеть как сфера.
Нормализация тоже выполняется достаточно просто, нам достаточно разделить значения вектора по xyz на общую длину вектора. Длину вектора можно вычислить с помощью теоремы Пифагора.
В представленном ниже коде вычисление нормализации сначала выполняется для одной грани. Затем вычисляется шум одновременно для всех шести рёбер, потому что для получения позиции следующей грани нужно всего лишь перевернуть значения по xyz.
// 3D panoramical cube map
document.body.addChild('h2').innerText = '3D panoramical cube map';
// we're not using the drawNoise function because our canvas is rectangular
var mCubemap = document.createElement('canvas')
,iW = 6*iSize;
mCubemap.width = iW;
mCubemap.height = iSize;
var iHSize = iSize/2 // half the size of the cube
,oCtx = mCubemap.getContext('2d')
,oImgData = oCtx.getImageData(0,0,iW,iSize)
,aPixels = oImgData.data
,aa = 123
,bb = 231
,cc = 321
;
for (var i=0,l=iSize*iSize;i<l;i++) {
var x = i%iSize // x position in image
,y = (i/iSize)<<0 // y position in image
,a = -iHSize + x+.5 // x position on the cube plane, the added .5 is to get the center of the pixel
,b = -iHSize + y+.5 // y position on the cube plane
,c = -iHSize // z position of the cube plane
,fDistanceAB = Math.sqrt(a*a+b*b) // to calculate the vectors length we use Pythagoras twice
,fDistanceABC = Math.sqrt(fDistanceAB*fDistanceAB+c*c)
,fDrds = .5*fDistanceABC // adjust the distance a bit to get a better radius in the noise field
,v = 1
;
a /= fDrds; // normalize the vector
b /= fDrds; // normalize the vector
c /= fDrds; // normalize the vector
//
// since we now know the spherical position for one plane we can derive the positions for the other five planes simply by switching the x, y and z values (the a, b and c variables)
var aNoisePositions = [
[a,b,c] // back
,[-c,b,a] // right
,[-a,b,-c] // front
,[c,b,-a] // left
,[a,c,-b] // top
,[a,-c,b] // bottom
];
for (var j=0;j<6;j++) {
v = Simplex.noise(
aa + aNoisePositions[j][0]
,bb + aNoisePositions[j][1]
,cc + aNoisePositions[j][2]
);
var pos = 4*(y*iW+j*iSize+x); // the final position of the rgba pixel
aPixels[pos] = aPixels[pos+1] = aPixels[pos+2] = v*255<<0;
aPixels[pos+3] = 255;
}
}
oCtx.putImageData(oImgData,0,0);
document.body.addChild('img',{src:mCubemap.toDataURL("image/jpeg")});Вот шесть сторон, составленные в одно изображение, плюс скриншот того, как это выглядит при взгляде из куба. В исходном коде есть 3D-пример, написанный на threejs.

Кубическая панорамная карта

Бесшовное 2D-изображение
Может показаться, что бесшовное 2D-изображение реализовать легко, но мне кажется, что это самое сложное из описанного в статье, потому что для его понимания необходимо думать в четырёх измерениях. Ближе всего к этому была цилиндрическая карта (с повторением по горизонтали), поэтому мы возьмём её за основу. В цилиндрической карте мы использовали для окружности горизонтальную позицию изображения; то есть горизонтальная позиция изображения даёт нам две координаты x и y в поле шума xyz. Вертикальная позиция изображения соответствует z в поле шума.
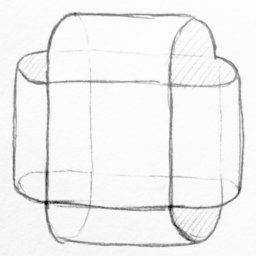
Мы хотим, чтобы изображение было бесшовным и по вертикали, поэтому если добавим ещё одно измерение, то сможем использовать его для создания второй окружности и замены линейного значения z поля. Это похоже на создание двух цилиндров в четырёхмерном поле. Я попробовал визуализировать это на эскизе, он неточный, но я пытался передать общий принцип, а не нарисовать четырёхмерный цилиндр.

Эскиз двух цилиндров в четырёх измерениях
Код довольно прост: это всего лишь две окружности в четырёхмерном пространстве шума.
// four dimensional tile
fNoiseScale = .003;
drawNoise(function(i,x,y){
var fNX = x/iSize
,fNY = y/iSize
,fRdx = fNX*2*Math.PI
,fRdy = fNY*2*Math.PI
,a = fRds*Math.sin(fRdx)
,b = fRds*Math.cos(fRdx)
,c = fRds*Math.sin(fRdy)
,d = fRds*Math.cos(fRdy)
,v = Simplex.noise(
123+a*fNoiseScale
,231+b*fNoiseScale
,312+c*fNoiseScale
,273+d*fNoiseScale
)
;
return (Math.min(Math.max(2*(v -.5)+.5,0),1)*255)<<0;
}).img().div(2,2);И вот результат:



GennPen
А как решается проблема подобных бесшовных текстур когда сильно отдаляешь камеру, когда начинает проявляться сетка?
MrSmith33
Например: How to Tile a Texture Without Repetition — Blender Tutorial