Уже год как я сменил работу на новую. В этой статье я хочу поделиться опытом, накопленным на прошлом месте. Здесь рассмотрены методы аппроксимации кривых Безье, а также обработка исключительных случаев, при которых простые алгоритмы показывают себя не очень хорошо. Все, кому близка тема векторной графики — прошу под кат.

Введение

На предыдущей работе я был оператором ЧПУ-станка, делал мебельные фасады из МДФ. Работа разнообразная: то сидишь за компом и чертишь в CAD/CAM-программе, то стоишь контролируешь резку, то приносишь заготовки и уносишь готовые детали.

До того, как я пришёл в фирму, там был довольно скудный каталог рисунков, которого явно не хватало клиентам, поэтому они всё время просили сделать как на фото из интернета. Все специфичные рисунки я рисовал вручную, стандартные же были довольно просты, а так как я увлекался программированием, то решил генерировать их G-код для станка напрямую без участия CAD/CAM-программы.

В интернете существует пара вариантов в виде макросов для CorelDRAW и что-то ещё в этом духе. Я же решил придумать более лёгкое, быстрое и кроссплатформенное решение, которое решило бы мои текущие задачи максимально эффективно. Выбор был сделан в пользу консольной программы с выводом результата в stdout.

В данной статье я не буду затрагивать саму программу, поскольку это тема отдельной статьи. Я расскажу о том, с чем мне пришлось столкнуться в самом начале, а именно как представить кривую Безье в виде прямых отрезков с точностью, при которой будет создаваться минимальное количество промежуточных точек при сохранении визуальной плавности на изделии. Станок очень хорошо передаёт издаваемыми звуками то, насколько плавно он движется по траектории. Я ориентировался на звук при резке чертежей, созданных профессиональной CAD/CAM-программой.

На тот момент самой дельной информацией по этому вопросу была вот эта статья на RSDN. Статья заслуживает внимания. В ней много скриншотов демонстрационной программы. Перед написанием статьи я зашёл на страницу и обнаружил, что ссылки на программу и её исходный код мёртвые. Как подсказали в комментариях, теперь исходный код demo-программы лежит на SourceForge. Вот ссылка.

С чем мы собираемся бороться?

Итак, начнём. На более прямых участках нужно минимальное количество точек, но в определённых местах, таких как крутые повороты, перегибы и узкие петли, кривая очень сильно изгибается, и чтобы сохранить плавность, нужно генертровать больше точек. Потому разбиение и называется адаптивным. Ниже примеры кривых, которые обычно сложно аппроксимировать.

Рис. 1 — Крутой поворот

Рис. 2 — Перегиб

Рис. 3 — Узкая петля

В общем-то внешне это примерно одно и то же. И тут мой подход отличается от подхода автора той статьи. Он решил обрабатывать все исключительные ситуации в отдельности. Как итог — нагромождение кода, который тем не менее не особо-то эффективно решает все проблемы. Я начал искать решение, которое было бы простым и универсальным. Лень — двигатель прогресса. В итоге все проверки сводятся к одной, а степень детализации задаётся одним параметром.

Кривые 2-го порядка

Первый пример будет с кривой Безье 2-го порядка. Начальная и конечная точки эталонной кривой совпадают с таковыми у исходной. Опорная точка находится посередине, т.к. кривая 2-го порядка, а значит мы делим её на две части.

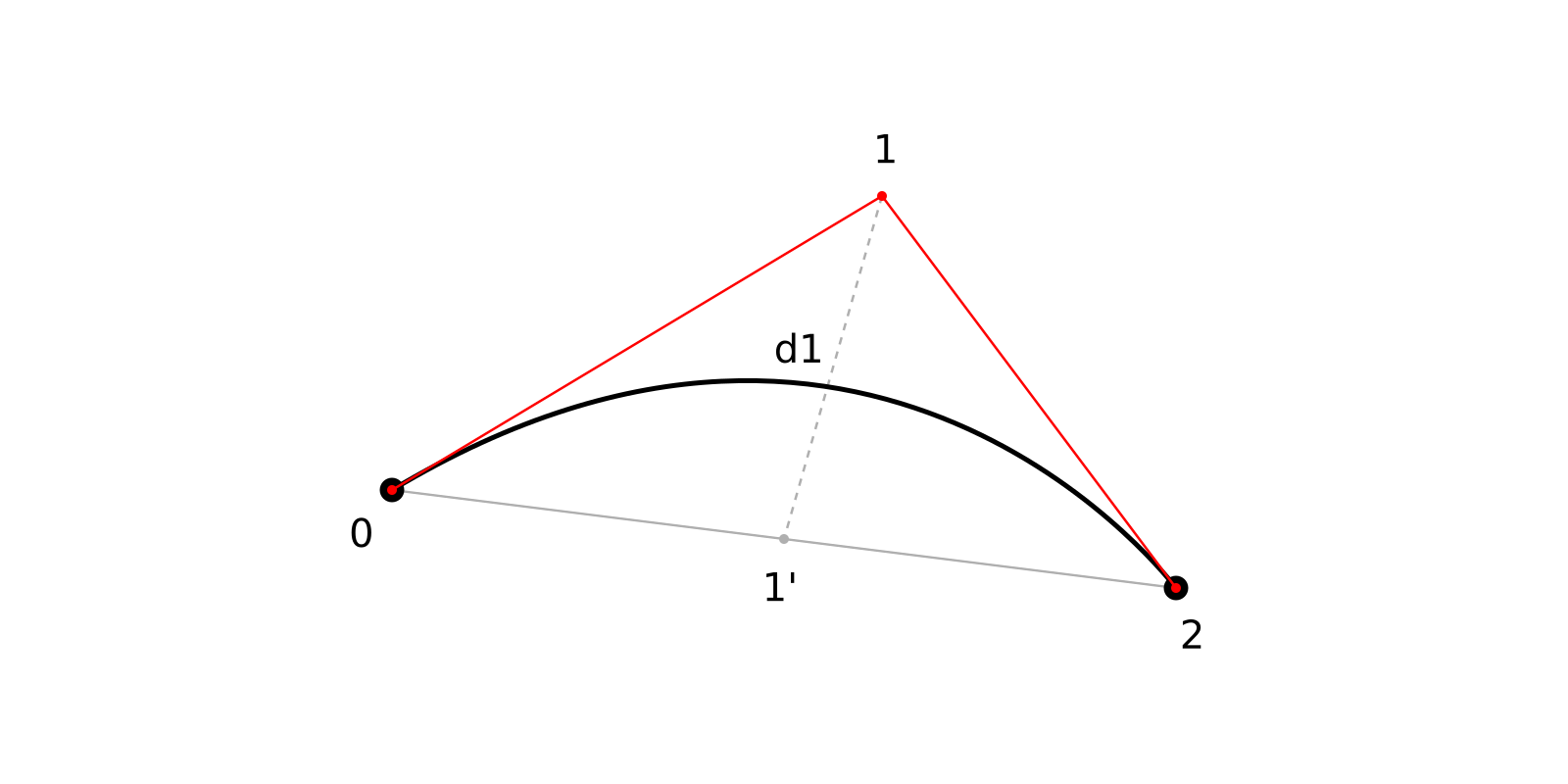
Рис. 4 — Кривая Безье 2-го порядка

Расстояние d1 на рисунке показывает, на сколько исходная опорная точка удалена от эталонной (отрезок 1-1'). Если d1 меньше заданной нами величины, чертим прямую линию из точки 0 в точку 2 и заканчиваем аппроксимацию, если нет — делим кривую пополам и рекурсивно для каждой половины повторяем проверку. Извините frontend-разработчики, джаваскрипта не будет. Ниже пример кода на питоне.

from math import sqrt


def b2(x0, y0, x1, y1, x2, y2, d):
    mx1 = x1 - (x0 + x2) / 2
    my1 = y1 - (y0 + y2) / 2
    d1 = sqrt(mx1 ** 2 + my1 ** 2)
    if d1 < d:
        print(x2, y2)
    else:
        x01 = (x0 + x1) / 2
        y01 = (y0 + y1) / 2
        x12 = (x1 + x2) / 2
        y12 = (y1 + y2) / 2
        x012 = (x01 + x12) / 2
        y012 = (y01 + y12) / 2
        b2(x0, y0, x01, y01, x012, y012, d)
        b2(x012, y012, x12, y12, x2, y2, d)

Кривые 3-го порядка

Второй пример будет с кривой Безье 3-го порядка. Начальная и конечная точки эталонной кривой совпадают с таковыми у исходной. Опорные точки находятся на 1/3 и 2/3 её длины, т.к. кривая 3-го порядка, а значит мы делим её на три части.

Рис. 5 — Кривая Безье 3-го порядка.

Аналогично предыдущему примеру, расстояния d1 и d2 на рисунке показывают отклонение опорных точек от их эталонных значений (отрезки 1-1' и 2-2'). Если оба расстояния d1 и d2 меньше заданной нами величины, чертим прямую линию из точки 0 в точку 3 и заканчиваем аппроксимацию, если нет — делим кривую пополам и рекурсивно для каждой половины повторяем проверку. Пример кода прилагается.

from math import sqrt


def b3(x0, y0, x1, y1, x2, y2, x3, y3, d):
    px = (x3 - x0) / 3
    py = (y3 - y0) / 3
    mx1 = x1 - x0 - px
    my1 = y1 - y0 - py
    mx2 = x2 - x3 + px
    my2 = y2 - y3 + py
    d1 = sqrt(mx1 ** 2 + my1 ** 2)
    d2 = sqrt(mx2 ** 2 + my2 ** 2)
    if d1 < d and d2 < d:
        print(x3, y3)
    else:
        x01 = (x0 + x1) / 2
        y01 = (y0 + y1) / 2
        x12 = (x1 + x2) / 2
        y12 = (y1 + y2) / 2
        x23 = (x2 + x3) / 2
        y23 = (y2 + y3) / 2
        x012 = (x01 + x12) / 2
        y012 = (y01 + y12) / 2
        x123 = (x12 + x23) / 2
        y123 = (y12 + y23) / 2
        x0123 = (x012 + x123) / 2
        y0123 = (y012 + y123) / 2
        b3(x0, y0, x01, y01, x012, y012, x0123, y0123, d)
        b3(x0123, y0123, x123, y123, x23, y23, x3, y3, d)

Выведение

Поскольку массово используются только кривые этих порядков, копать дальше считаю лишним. Этот код несколько лет помогал выполнять мне мою работу. Требования к плавности на станке высокие, вибрация его убивает. Станок жив до сих пор, поэтому код прошёл боевое крещение. При работе на станке все мои размеры были в миллиметрах, переменная d в моём случае была 0.025 мм.

Также есть материал по рациональным кривым тех же порядков (это те, что с весами). Если будет интерес, про это тоже напишу. Благодарю за прочтение.