Недавно видел статью об обработке столкновений. И там не было самого главного — алгоритма и реализации. Давайте заполним этот пробел и рассмотрим как находить и обрабатывать столкновения. Реализация будет на Java.
Предупреждаю, что в статье много кода.

Немного теории
Алгоритм основан на теореме о разделяющей оси. Для 3D случая это разделяющая плоскость.
Определение будет такое: если между двумя выпуклыми фигурами существует плоскость (для 2D прямая), относительно которой фигуры лежат по разные стороны, то такие фигуры не пересекаются.
Следствие, с помощью которого можно проверить разделяющая плоскость или нет: если взять нашу разделяющую плоскость и построить к ней перпендикулярную, то проекции фигур на полученную плоскость тоже не будут пресекается.
Для того чтобы найти (или не найти, если фигуры пересекаются) разделяющую плоскость необходимо собрать нормали сторон и построить к ним перпендикуляры. Эти перпендикуляры будут являться нормалями плоскостей, на которые нужно будет строить проекции моделей. При этом нам не нужно знать координаты плоскости, будем считать, что все они проходят через центр. На рисунке ниже представлена проверка одной из сторон.
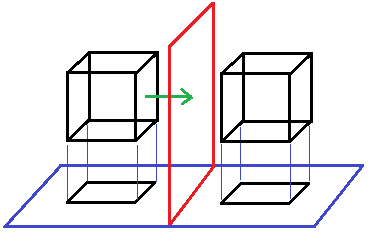
Зеленым обозначена нормаль стороны фигуры, которую проверяем. Красным — разделяющая плоскость. Синим плоскость на которую мы должны строить проекции. Как видно если взять нормаль синей плоскости, то она будет перпендикулярна нормали проверяемой нами стороны.
Теперь у нас есть по две проекции моделей на каждой плоскости. Нужно найти хотя бы одну плоскость, где проекции не пересекаются. Для этого можно применить эту же теорему, только для 2D случая (подробнее в реализации). Если мы такую найдем, то модели не пересекаются. Соответственно, если не найдем — пересекаются.
Алгоритм
Исходя из теории можно составить следующий алгоритм работы:
- Находим все нормали объектов. (собираем нормали с обоих объектов)
- По нормалям находим плоскости на которые будем строить проекции.
Далее работаем отдельно с каждой плоскостью.
- Ищем проекции моделей на плоскость.
- Проверяем пересекаются ли проекции. Если нет, то наши объекты тоже не пересекаются.
Алгоритм проверки пересечения проекций:
Собираем все стороны проекций и далее работаем с ними.
- Ищем перпендикуляр к стороне.
- Строим на этот перпендикуляр проекции фигур. Если проекции не пересекаются, значит и наши фигуры тоже.
Реализация
Далее разберем полноценную реализацию нахождения и обработки пересечений.
Небольшое отступление:
Выложенный код я не буду сокращать (дьявол кроется в деталях), только дописывать комментарии, возможно каких то интересующих вас методов я не выложу, но их можно легко найти в репозитории на GitHub, также я буду оставлять ссылки на классы.
Следуя алгоритму, начнем с поиска всех плоскостей. Предполагается что нормали мы знаем (загрузили их из файла модели).
Очень важно отсеять одинаковые плоскости, алгоритм очень сложный в плане затрат, и любая оптимизация будет уместна. В данном случае она не любая и уменьшение количества проверяемых плоскостей очень сильно влияет на скорость его работы.
Для физических моделей в игре я использую только параллелепипеды, никаких сложных фигур. В итоге в худшем случае мы будем проверять 6 плоскостей.
Прежде чем приступить следует рассмотреть интерфейс, который я буду использовать ниже.
public interface ICollidable
{
// Метод для оптимизаций.
// Если сферы описанные вокруг моделей не пересекаются, то и объекты не пересекаются.
float getRadius();
Vector3 getPosition();
ArrayList<Vector2> getConvexHull(Plane plane); // Поиск проекции на плоскость (метод будет рассмотрен ниже)
ArrayList<Vector3> getNormals();
void normalizeLocation();
}
private static ArrayList<Plane> getPlanes(ICollidable firstPh, ICollidable secondPh)
{
ArrayList<Plane> planes = new ArrayList<>();
ArrayList<Vector3> firstNormals = firstPh.getNormals();
ArrayList<Vector3> secondNormals = secondPh.getNormals();
Plane plane = new Plane();
int size = firstNormals.size() + secondNormals.size();
for(int i = 0; i < size; i++)
{
setPlane(plane, firstNormals, secondNormals, i);
if (!planes.contains(plane))
planes.add(new Plane(plane));
}
return planes;
}
private static void setPlane(Plane plane, ArrayList<Vector3> firstNormals, ArrayList<Vector3> secondNormals, int num)
{
// Устанавливаем плоскость из нормали (нам не важна позиция и направление x, y осей)
if (num < firstNormals.size())
plane.setFrom(firstNormals.get(num));
else
{
num -= firstNormals.size();
plane.setFrom(secondNormals.get(num));
}
// Берем перпендикулярную плоскость.
plane.swapZY();
}
Исходный код класса Plane, Vector3
Итак, у нас есть плоскости которые нужно проверить. Для этого на каждую плоскость построим проекции моделей. Если мы не найдем плоскостей на которых проекции не пересекаются, то нам необходимо найти плоскость на которой модели пересекаются меньше всего, из этого пересечения нужно извлечь вектор. Это будет тот вектор, на который необходимо передвинуть одну из моделей, чтобы они больше не пересекались.
Вектор мы изначально получим на плоскости. Поэтому хоть направление осей плоскости X и Y нам не важно, тем не менее мы должны их сохранить, так как вектор необходимо будет вернуть в 3D и они нам пригодятся.
Класс реализующий поиск пересечения моделей: Collision3D
Код выполняющий алгоритм выше:
private static CheckResult check(ICollidable firstPh, ICollidable secondPh)
{
// Собираем плоскости которые нужно проверить
ArrayList<Plane> planes = getPlanes(firstPh, secondPh);
Collision2D min = null;
Plane minPlane = new Plane();
for (Plane plane : planes)
{
// Получаем проекции моделей на плоскость.
ArrayList<Vector2> resultOne = firstPh.getConvexHull(plane);
ArrayList<Vector2> resultTwo = secondPh.getConvexHull(plane);
// Проверяем пересекаются проекции или нет. (код проверки будет рассмотрен ниже в методе "check")
Collision2D collision = new Collision2D(resultOne, resultTwo);
Vector.release(resultOne);
Vector.release(resultTwo);
if (!collision.isCollide())
return null;
// Сразу же ищем коллизию с минимальной длинной вектора пересечения
if (min == null || collision.getMTVLength() < min.getMTVLength())
{
min = collision;
minPlane.setFrom(plane);
}
plane.release();
}
return new CheckResult(min, minPlane);
}
Рассмотрим детальнее каким образом мы получаем проекции. Тут полная реализация.
Собственно найти саму проекцию не сложно, но от самой проекции никакого толка не будет. Для дальнейшей обработки необходимо правильно найти стороны фигуры. Также она должна быть выпуклой, на картинке ниже объяснено почему.
Вогунтая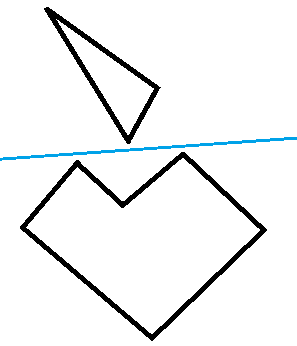 |
Выпуклая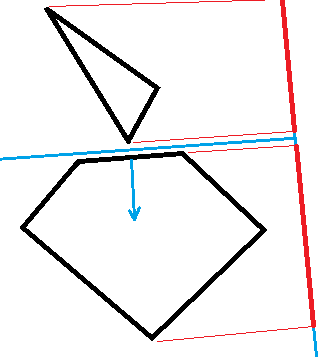 |
Как видно на первом рисунке (с вогнутой фигурой) алгоритм посчитает что фигуры пересекаются, хотя разделяющую ось мы построить можем. Так как ось ищется исходя из сторон фигуры, а параллельной стороны к оси в данном случае нет. На втором рисунке по вогнутой фигуре составлена МВО. Здесь алгоритм найдет ось. Для нахождения оболочки я реализовал алгоритм Грэхема.
Ниже функция нахождения простой проекции — набора точек спроецированных на плоскость.
private ArrayList<Vector2> getDistinctProjection(Plane plane)
{
Vector2 vector = Vector.getInstance(2);
// Можно было бы исользовать HashSet но я не уверен в большом выигрыше производительности (точек не так много)
ArrayList<Vector2> result = new ArrayList<>();
for (Vector3 current : vertices)
{
plane.getProjection(vector, current);
if (!result.contains(vector)) // Отсеиваем уже существующие точки
{
Vector2 copy = Vector.getInstance(2, vector);
result.add(copy);
}
}
Vector.release(vector);
return result;
}
// Метод из класса Plane:
public void getProjection(Vector2 result, Vector3 vector)
{
throwIfReleased();
float x = vector.getX() * xAxis.getX() + vector.getY() * xAxis.getY() + vector.getZ() * xAxis.getZ();
float y = vector.getX() * yAxis.getX() + vector.getY() * yAxis.getY() + vector.getZ() * yAxis.getZ();
result.setFrom(x, y);
}
Теперь пришло время посмотреть на реализацию построения МВО.
Действие можно расписать на четыре шага.
- Поиск проекции.
- Выбор опорной точки.
- Сортировка остальных точек относительно опорной.
- Удаление лишних точек.
Выпуклой оболочкой множества X называется наименьшее выпуклое множество содержащее X. «Наименьшее множество» здесь означает наименьший элемент по отношению к вложению множеств, то есть такое выпуклое множество, содержащее данную фигуру, что оно содержится в любом другом выпуклом множестве, содержащем данную фигуру.
Также там есть пример:
Представьте себе доску, в которую вбито — но не по самую шляпку — много гвоздей. Возьмите верёвку, свяжите на ней скользящую петлю (лассо) и набросьте её на доску, а потом затяните. Верёвка окружает все гвозди, но касается она только некоторых, самых внешних. Те гвозди, которых она касается, составляют выпуклую оболочку для всей группы гвоздей[1].
Хорошая статья по построению минимальной выпуклой оболочки.
@Override
public ArrayList<Vector2> getConvexHull(Plane plane)
{
// Ищем проекцию
ArrayList<Vector2> projection = getDistinctProjection(plane);
ArrayList<Vector2> convexHull = new ArrayList<>(projection.size());
if (projection.size() < 2)
throw new IllegalStateException("projection size less than 2");
// Ищем первую точку, которая 100% входит в МВО
// и удаляем ее из проекции
// также она будет являться опорной, для сортировки.
int firstIndex = getFirstPointIndex(projection);
Vector2 first = projection.remove(firstIndex);
convexHull.add(first);
// Сортируем оставшиеся точки против часовой стрелки
Collections.sort(projection, new AngleComparator(first));
// Забираем вторую точку, т.к. алгоритму ниже она необходима для работы.
Vector2 second = projection.remove(0);
convexHull.add(second);
Vector2 prevVector = Vector.getInstance(2);
Vector2 currentVector = Vector.getInstance(2);
for(Vector2 current : projection)
{
Vector2 firstPrevPoint = convexHull.get(convexHull.size() - 1);
Vector2 secondPrevPoint = convexHull.get(convexHull.size() - 2);
// Предыдущий вектор
prevVector.setFrom(firstPrevPoint);
prevVector.subtract(secondPrevPoint);
// Новый вектор
currentVector.setFrom(current);
currentVector.subtract(firstPrevPoint);
// Если угол между предыдущим и новым вектором получился развернутый, мы удаляем предыдущую точку
float angle = prevVector.getAngle(currentVector);
if (angle >= 180 && angle < 360)
convexHull.remove(convexHull.size() - 1);
// И всегда добавляем текущую
convexHull.add(current);
}
Vector.release(prevVector);
Vector.release(currentVector);
return convexHull;
}
// Поиск угла из класса Vector2
public float getAngle(Vector2 other)
{
throwIfReleased();
float scalar = getScalar(other);
float lengthOne = this.getLength();
float lengthTwo = other.getLength();
float angle = (float)Math.toDegrees(Math.acos(scalar / (lengthOne * lengthTwo)));
return Angle.correct(getCross(other) > 0 ? angle : 360 - angle);
}
Первую точку, которая должна входить в МВО, я выбираю самую правую. Если таких нашлось больше чем одна, то выбираем из них самую верхнюю.
private static int getFirstPointIndex(ArrayList<Vector2> projection)
{
Vector2 minVector = null;
int minVectorIndex = 0;
int size = projection.size();
for (int i = 0; i < size; i++)
{
Vector2 current = projection.get(i);
if (minVector == null)
{
minVector = current;
continue;
}
int compareX = Float.compare(current.getX(), minVector.getX());
if (compareX < 0)
{
minVector = current;
minVectorIndex = i;
}
if (compareX == 0)
{
int compareY = Float.compare(current.getY(), minVector.getY());
if (compareY == 0)
throw new IllegalArgumentException("projection has the same points");
if (compareY > 0)
{
minVector = current;
minVectorIndex = i;
}
}
}
return minVectorIndex;
}
Самым забагованным местом у меня была сортировка точек против часовой стрелки. В начале были просто неправильные реализации, а потом много времени понадобилось чтобы понять какие есть исключительные ситуации. Для себя даже комментарии написал, чтобы не забыть что к чему.
Сортирую точки относительно первой по углам. Если у точек углы равны, то я сравниваю их по расстоянию от первой причем по разному в зависимости от того, как точки лежат — выше или ниже опорной. Если ниже, то первой должна идти та, до которой расстояние меньше. Если выше — наоборот.
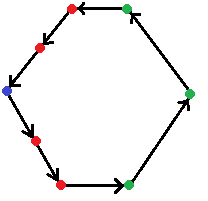
Синяя точка — опорная. Зеленые — обычные точки. Красные — с одинаковыми углами. Схема обхода демонстрирует описанный выше алгоритм сортировки.
Также нужно не забыть нормализовать углы для нормальной сортировки, в коде будет пример.
private static class AngleComparator implements Comparator<Vector2>
{
private Vector2 first;
private Vector2 left;
private Vector2 right;
public AngleComparator(Vector2 first)
{
this.first = first;
left = Vector.getInstance(2);
right = Vector.getInstance(2);
}
@Override
public int compare(Vector2 lhs, Vector2 rhs)
{
// сортируем против часовой стрелки
// сдвигаем точки к центру
left.setFrom(lhs);
left.subtract(first);
right.setFrom(rhs);
right.subtract(first);
// ищем углы относительно оси Х
float firstAngle = Vector2.xAxis.getAngle(left);
float secondAngle = Vector2.xAxis.getAngle(right);
// для правильной сортировки нормализуем углы
// Пример: 15, 45, 315, 345 (неправильная) => -45, -15, 15, 45 (правильная)
if (firstAngle > 90)
firstAngle -= 360;
if (secondAngle > 90)
secondAngle -= 360;
// если углы одинаковые мы должны сравнить их по длинне
// причем если точка выше оси Х то та что ближе будет идти позже
// и на оборот для случая когда точка ниже оси Х.
// Выше или ниже, я сравниваю по углу
// Если углы одинаковые сравниваем по длинне
if (Math.abs(firstAngle - secondAngle) <= Vector.epsilon)
{
float leftLength = left.getLength();
float rightLength = right.getLength();
// Если угол больше 0, выполняем обратную сортировку
if (firstAngle >= 0)
return Float.compare(rightLength, leftLength);
return Float.compare(leftLength, rightLength);
}
// если никаких экзотических случаев нету просто сравниваем по углам
return Float.compare(firstAngle, secondAngle);
}
}
С поиском проекции разобрались, теперь необходимо понять как находить пересечения двух проекций. Логика остается такой же как и при 3D.
Дальше я эти проекции буду называть фигурами, потому как строить дальше мы будем проекции проекций, извиняюсь за тавтологию.
Перебирая все стороны полученных фигур ищем нормали. Далее строим проекцию фигуры на найденную нормаль, если найдена хоть одна прямая на которой проекции не пересекаются то и что? Неожиданно, но и фигуры (как и 3D модели) не пресекаются в таком случае. :)
Полная реализация класса тут: Collision2D
private static CheckResult check(ArrayList<Vector2> firstVertices, ArrayList<Vector2> secondVertices)
{
Vector2 mtv = null;
Vector2 normal = Vector.getInstance(2);
float minMTVLength = 0.0f;
int count = firstVertices.size() + secondVertices.size();
for (int i = 0; i < count; i ++)
{
setNormal(normal, firstVertices, secondVertices, i);
// Находим проекции фигур на нормали сторон. X - максимальная координата Y - минимальная.
Vector2 firstProjection = normal.getProjection(firstVertices);
Vector2 secondProjection = normal.getProjection(secondVertices);
// Если хотя бы на одной проекции фигуры не пересекаются, значит существует разделяющая ось, и фигуры вообще не пересекаются.
if (firstProjection.getX() < secondProjection.getY() || secondProjection.getX() < firstProjection.getY())
return null;
// Выбираем минимальный вектор. Для нахождения вектора, по которому будем разрешать пересечение.
if (mtv == null)
{
mtv = Vector.getInstance(2, normal);
minMTVLength = getIntersectionLength(firstProjection, secondProjection);
}
else
{
float mtvLength = getIntersectionLength(firstProjection, secondProjection);
if (Math.abs(mtvLength) < Math.abs(minMTVLength))
{
mtv = Vector.getInstance(2, normal);
minMTVLength = mtvLength;
}
}
}
return new CheckResult(mtv, minMTVLength);
}
// Метод из класса Vector2
public Vector2 getProjection(ArrayList<Vector2> vertices)
{
Vector2 result = null;
for (Vector2 current : vertices)
{
float projection = getScalar(current);
if (result == null)
result = new Vector2(projection, projection);
// x - max
if (projection > result.getX())
result.setX(projection);
// y - min
if (projection < result.getY())
result.setY(projection);
}
return result;
}
private static float getIntersectionLength(Vector2 firstProjection, Vector2 secondProjection)
{
return (secondProjection.getY() - firstProjection.getX() > 0)
? secondProjection.getY() - firstProjection.getX()
: firstProjection.getY() - secondProjection.getX();
}
private static void setNormal(Vector2 normal, ArrayList<Vector2> vertices, int num)
{
Vector2 firstPoint = vertices.get(num);
Vector2 secondPoint = vertices.get(num + 1 == vertices.size() ? 0 : num + 1);
Vector2 edge = secondPoint.getSubtract(firstPoint);
normal.setX(-edge.getY());
normal.setY(edge.getX());
normal.normalize();
}
Сразу же в методе выше мы ищем минимальный вектор пересечения, если фигуры не пересекаются он нам, конечно, не понадобится. А если пересеклись, то его необходимо преобразовать в 3D, чтобы модели можно было отодвинуть друг от друга. Сделать это можно с помощью метода ниже.
private static Vector3 getMTV(CheckResult result)
{
Vector2 mtv2 = result.collision.getMTV();
Vector3 mtv3 = new Vector3(mtv2.getX(), mtv2.getY(), 0);
Vector3 planeX = result.plane.xAxis();
Vector3 planeY = result.plane.yAxis();
Vector3 planeZ = result.plane.zAxis();
float[] matrix = new float[16];
matrix[0] = planeX.getX();
matrix[1] = planeX.getY();
matrix[2] = planeX.getZ();
matrix[4] = planeY.getX();
matrix[5] = planeY.getY();
matrix[6] = planeY.getZ();
matrix[8] = planeZ.getX();
matrix[9] = planeZ.getY();
matrix[10] = planeZ.getZ();
matrix[15] = 1.0f;
Matrix.multiplyMV(mtv3.getRaw(), 0, matrix, 0, mtv3.getRaw(), 0);
mtv3.normalize();
return mtv3;
}
На этом в принципе и все, всего описанного выше достаточно, что бы определить пересечение 3D моделей.
Применение алгоритма
Вместо вывода напишу, что проверка на пересечение двух объектов занимает много времени. Как уже говорил, я не использую сложных коллижн моделей. Также применяю ряд оптимизаций таких как расчет радиуса сферы, описанной вокруг модели, пересечение сфер ведь сравнить намного проще. У тех же объектов сферы которых пересекаются, детальный поиск пересечений выполняется параллельно.
Исходники игры находятся тут: github.com/Nirklav/Tanks
Комментарии (24)

Allen
25.08.2015 12:32А что если сталкивать тетраэдры их основаниями? Алгоритм сработает?
Ведь нормали все в разные стороны, а коллизия проекций будет хорошо видна только в одной плоскости.
Проекция в виде отрезка детектируется?
Nirvano
25.08.2015 12:38Сработает, ведь мы строим проекции на плоскость, нормаль которой перпендикулярна нормали стороны. Смотрите на картинку с кубами, ситуация в принципе аналогичная.

Allen
25.08.2015 12:42А как вы выбираете перпендикулярную плоскость? Ведь их там
всё небо в попугаяхбесконечное множество
Nirvano
25.08.2015 12:44Беру первую попавшуюся. Я строю плоскость по нормали, а потом меняю направление Y и Z осей. (Z в данном случае нормаль плоскости)
// Берем перпендикулярную плоскость. plane.swapZY();
Mrrl
25.08.2015 14:55Тогда для двух тетраэдров, сталкивающихся серединами рёбер, вы можете не найти нужной плоскости. Там удачных плоскостей (перпендикулярных как единственной разделяющей плоскости, так и какой-нибудь грани тетраэдра) всего 8.

Nirvano
25.08.2015 15:04Не могу себе представить случая когда фигуры пересекаются, и при этом не пересекают сторон. А если стороны пересекаются, то мы найдем пересечение.

Mrrl
25.08.2015 15:58+2Возьмите два тетраэдра.
Вершины первого: (0,-1,-1), (0,1,-1), (-1,0,0), (1,0,0)
Вершины второго: (0,-1,0.1), (0,1,0.1), (-1,0,1.1), (1,0,1.1)
Они не пересекаются. Нормали к граням каждого из них (с точностью до коэффициента) — (0,1,1), (0,-1,1), (1,0,1), (-1,0,1).
Если я правильно понял ваш алгоритм выбора перпендикулярной плоскости, то для этих векторов он выдаст их же, но в другом порядке (опять же с точностью до коэффициента): (0,-1,1), (0,1,1), (-1,0,1), (1,0,1).
Можно проверить, что проекции тетраэдров на каждую из плоскостей, перпендикулярную одному из этих векторов, будут пересекаться.
p53
25.08.2015 19:02+2Я разобрался в авторском алгоритме выбора перпендкулярной плоскости.
// from Vector3.orthogonal setFrom(-y, x, 0); // from Plane.setFrom zAxis.setFrom(normal); // = (x, y, z) xAxis.setFrom(normal); xAxis.orthogonal(); // = (-y, x, 0) // from Plane.swapZY -- странное название Vector3 temp = xAxis; xAxis = zAxis; zAxis = temp; // = (-y, x, 0)
То есть почти всегда перпендикулярная плоскость выбирается с нормалью (-y, x, 0). Так что для приведённого примера всё хорошо, и я поспешил нарисовать к нему картинку. Но стоит повернуть тетраэдры неудачно, как проблема снова возникает.

mbait
25.08.2015 14:35Не учтен случай, когда фигуры сталкиваются вершинами. Для этого в 2D к качестве разделяющей можно взять нормаль к прямой, проходящей через центры масс обеих фигур, в 3D — по тому же принципу.

Nirvano
25.08.2015 15:15Как я ответил на комментарий выше, не могу себе представить случай, когда фигуры пересекаются, и все их стороны — нет.
Если они просто соприкасаются вершинами, то да, я не считаю это пересечением.mbait
25.08.2015 15:33Возможно, вы правы. Когда-то очень давно я писал физ. библиотеку и тоже использовал разделяющую ось для поиска столкновений, но почему-то там был тест на столкновение углами, и чтобы он проходил, я добавил проверку, которую описал выше.

p53
25.08.2015 19:41+1Также не до конца понятно зачем нужен поиск минимальной оболочки, если изначально теорема справедлива для выпуклых тел, а любая проекция (как и сечение) выпуклого тела всегда выпукла.
Вообще, метод разделяющей оси в трёхмерном случае предполагает поиск оси, а не плоскости =) Если существует разделяющая плоскость, то проекция двух многогранников на нормаль к ней даст непересекающиеся отрезки (проверка непересечения в одномерном случае сильно проще). Количество претендентов на нормаль такой плоскости конечно: это нормали граней исходных многогранников + попарные векторные произведения сторон одного на сторону другого. Наконец, существуют эвристики, как найти эту нормаль эффективно.
Mrrl
25.08.2015 20:22Количество претендентов на нормаль такой плоскости конечно: это нормали граней исходных многогранников + попарные векторные произведения сторон одного на сторону другого
Тогда уж ещё плюс векторы, соединяющие вершины разных многогранников… Хотя нет, там сложнее.

Nirvano
25.08.2015 21:40Минимальная оболочка нужна была что бы найти правильные нормали сторон проекций многогранников. Далее которые я использую для проверки проекций на пересечение. Так как после поиска проекции (не МВО) я получаю какой то набор точек, и глядя на него непонятно как искать разделяющую ось.
Вообще, метод разделяющей оси в трёхмерном случае предполагает поиск оси, а не плоскости =) Если существует разделяющая плоскость, то проекция двух многогранников на нормаль к ней даст непересекающиеся отрезки (проверка непересечения в одномерном случае сильно проще). Количество претендентов на нормаль такой плоскости конечно: это нормали граней исходных многогранников + попарные векторные произведения сторон одного на сторону другого. Наконец, существуют эвристики, как найти эту нормаль эффективно.
Как я понял вы предлагаете увеличить кол-во плоскостей на которых следует проверять пересечения (Решение проблемы с тетраэдрами). При этом отказаться от промежуточного действия — построения проекций на плоскость. Вместо этого строить проекции сразу на нормаль проверяемой плоскости.
Единственное не понял что значит попарные векторные произведения сторон одного на сторону другого.
Огромное спасибо за комментарии.
Mrrl
25.08.2015 22:07+1Попарные векторные произведения — это когда берётся ребро одного многогранника, ребро другого, и строится прямая, перпендикулярная им обоим. Проверяются проекции на эту прямую. Повторить для всех пар рёбер.
Количество прямых, на которые идут проекции, окажется F1+F2+E1*E2, а общая сложность алгоритма — (F1+F2+E1*E2)*(V1+V2). Думаю, что это гораздо дешевле, чем возиться с двумерными проекциями.

p53
25.08.2015 22:08+1Я неточно выразился. Если U и V – множество рёбер одного и второго многранников соответственно, то все произведения u?v, где u?U, а v?V. В примере с тетраэдрами, два наиболее близких ребра дадут плоскость, которая им параллельна и которая разделяет тетраэдры.



p53
В теореме о разделяющей оси идёт речь про выпуклые фигуры. В статье это всплывает мельком в середине.