В прошлой части я рассказал о концепции инкременторов (Iterable) и показал, как они решают множество проблем, присущих стандартным интервалам. Сейчас я расширю эту концепцию, чтобы сделать программирование бесконечных интервалов более безопасным и эффективным делом.
Disclaimer: идеи в этом посте более умозрительные, чем в предыдущих. Я буду рад дискуссии.
Кроме решённых проблем, о которых я рассказывал в предыдущих постах, остались ещё две. Это:
iota_range – бесконечный интервал целых чисел, начинающийся с какого-то значения и продолжающийся вечно. Это отсортированный прямой интервал. Вот только алгоритмы бинарного поиска, работающие с отсортированными прямыми интервалами, не будут с ним работать. Нельзя покорить бесконечность делением (хорошая фраза получилась).
Можно ли исправить алгоритмы STL, чтобы они не ломались при получении бесконечного интервала? В их текущем виде, нет – нельзя на этапе компиляции передать информацию о том, что какой-то из итераторов обозначает бесконечный интервал. Задумайтесь вот над чем: следующий код точно сработает:
а вот такой будет работать «вечно»:
Если у rng.begin() тип тот же, что и у rng.end(), два вызова возвращают один и тот же экземпляр lower_bound. Функция не сможет определить, будет она работать вечно, или нет. Но если можно позволить сигнальному итератору быть другого типа, у нас получится провести эту проверку на этапе компиляции.
Допустим, у нас есть функция типа (метафункция) под названием DenotesInfiniteSequence, которая принимает пару типов (BeginType, EndType) и говорит, будет ли последовательность бесконечной. Мы уже определили, что если BeginType и EndType одинаковые, то DenotesInfiniteSequence должна возвращать false, поскольку она не сможет никак это проверить. Но если они разные – допустим, EndType будет типа unreachable_sentinel или что-то типа того, то мы будем знать ещё на этапе компиляции, что последовательность бесконечная.
Некоторые интервалы по определению будут бесконечными, даже имея начальный и конечный итератор одинаковых типов.
Хотелось бы сразу отлавливать подобные ошибки, но, очевидно, бинарная функция DenotesInfiniteSequence с этим не справится. Для нулей типы BeginType и EndType будут одинаковыми, так что DenotesInfiniteSequence вернёт false.
Поэтому надо сконструировать унарную функцию типов IsInfinite, принимающую тип интервала.
Её можно использовать для определения концепции FiniteIterable
Каждый FiniteIterable является Iterable. Наблюдается параллельная иерархия уточнений:
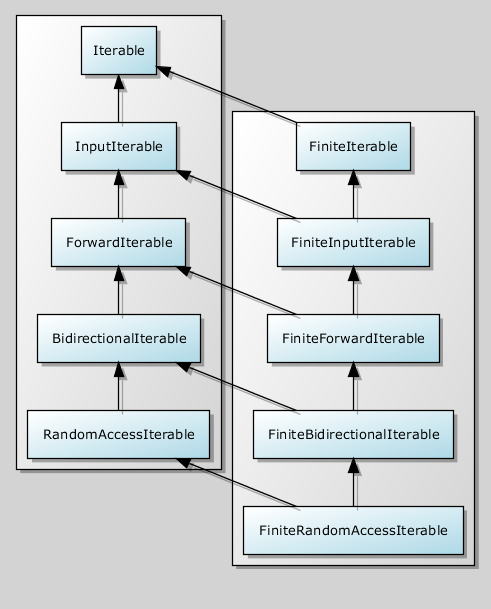
И все эти концепции, по аналогии с Range, не нужно определять в коде. Конечность ортогональна иерархии Iterable, и её можно опрашивать отдельно.
Но почему FiniteIterable, а не InfiniteIterable? Всё дело в алгоритмах и их требованиях. Нет алгоритмов, которые требуют, чтобы их аргументы интервалов были бесконечными. Поэтому бесполезно было бы иметь возможность писать InfiniteIterable. А вот алгоритм вроде lower_bound хотел бы, чтобы интервал был конечным. От этого и FiniteIterable.
Значит, все итераторы моделируют FiniteIterable по умолчанию, и тип должен как-то научиться быть бесконечным. Как? Можно специализировать is_infinite. К счастью, инструменты для создания инкременторов и интервалов принимают опциональный параметр IsInfinite, поэтому это сделать легко. Вот как теперь выглядит класс zeroes:
Добавив концепцию FiniteIterable мы даём алгоритмам, которым требуется конечность, возможность проверить это на этапе компиляции.
Теперь нам надо разделить интервалы на категории. По идее, либо он бесконечный, либо конечный – не так ли? Вообще-то, нет. Возьмём istream. Он может быть конечным, может не быть. Обычно поток прекращается, но иногда…
Ситуация сложная. Нужно ли запрещать передачу istream в алгоритм только из-за того, что он может быть бесконечным?
С бесконечными интервалами есть такая трудность: у всех итераторов и всех инкременторов есть связанный с ними difference_type. Александр Степанов пишет об этом:
Получается, что нам требуется целый тип бесконечного размера. Есть ли решение этой задачи?
Мне, конечно, не нравится всё, что замедляет работу алгоритмов, поэтому std::ptrdiff_t вполне можно оставить в качестве difference_type по умолчанию. Кроме этого, нужно разработать интерфейсы интервалов так, чтобы дать пользователям возможность задавать другой difference_type, если они заботятся о переполнении. Поэтому мне нравятся варианты 4 и 5. Другие библиотечные типы вроде bigint или safe_int с определёнными ограничениями было бы неплохо иметь возможность применить – если бы пользователь мог указать их использование, меняя скорость на безопасность, когда ему это нужно.
Возможно, читая предыдущие посты, вы были излишне оптимистичны: всё вроде бы начинало получаться, а теперь вы запутались. Но мне кажется, что мы неплохо продвинулись, по сравнению с тем, откуда начинали. Я описал 5 проблем с интервалами, использующими пару итераторов. Новая концепция инкременторов решает 3 из них, 4-ю проблему (бесконечные интервалы) теоретически можно решить улучшением этой концепции. И есть несколько вариантов работы с 5-й (переполнением). По крайней мере, начало положено.
Некоторые спрашивают – планирую ли я донести свои идеи до комитета по стандартизации С++. Разумеется. Когда мы получим поддержку концепций в языке, появится потребность в концептуализированной версии STL, возможно, работающей в другом пространстве имён.
А пока я займусь обсуждением вопроса в рассылке SG9 (Ranges) (http://www.open-std.org/mailman/listinfo/ranges). Этот спорный вопрос наверняка сможет породить новые идеи. Интересующихся призываю присоединяться к обсуждению.
Автор донес свои идеи до комитета и сейчас занимается их реализацией.
Другие статьи цикла
Интервалы в С++, часть 1: Интервалы с ограничителями
Интервалы в С++, часть 2: Бесконечные интервалы
Интервалы в С++, часть 3: представляем инкременторы (Iterable)
Disclaimer: идеи в этом посте более умозрительные, чем в предыдущих. Я буду рад дискуссии.
Кроме решённых проблем, о которых я рассказывал в предыдущих постах, остались ещё две. Это:
- Некоторые алгоритмы STL не работают с бесконечными интервалами
- Бесконечные или возможно бесконечные интервалы приводят к переполнению difference_type
Бесконечные итераторы
iota_range – бесконечный интервал целых чисел, начинающийся с какого-то значения и продолжающийся вечно. Это отсортированный прямой интервал. Вот только алгоритмы бинарного поиска, работающие с отсортированными прямыми интервалами, не будут с ним работать. Нельзя покорить бесконечность делением (хорошая фраза получилась).
Можно ли исправить алгоритмы STL, чтобы они не ломались при получении бесконечного интервала? В их текущем виде, нет – нельзя на этапе компиляции передать информацию о том, что какой-то из итераторов обозначает бесконечный интервал. Задумайтесь вот над чем: следующий код точно сработает:
// быстро заканчивается:
iota_range<bigint> rng;
auto i = std::lower_bound(rng.begin(),
std::next(rng.begin(), 10),
5);
а вот такой будет работать «вечно»:
// будет работать «вечно» :'-(
iota_range<bigint> rng;
auto i = std::lower_bound(rng.begin(),
rng.end(),
5);
Если у rng.begin() тип тот же, что и у rng.end(), два вызова возвращают один и тот же экземпляр lower_bound. Функция не сможет определить, будет она работать вечно, или нет. Но если можно позволить сигнальному итератору быть другого типа, у нас получится провести эту проверку на этапе компиляции.
Допустим, у нас есть функция типа (метафункция) под названием DenotesInfiniteSequence, которая принимает пару типов (BeginType, EndType) и говорит, будет ли последовательность бесконечной. Мы уже определили, что если BeginType и EndType одинаковые, то DenotesInfiniteSequence должна возвращать false, поскольку она не сможет никак это проверить. Но если они разные – допустим, EndType будет типа unreachable_sentinel или что-то типа того, то мы будем знать ещё на этапе компиляции, что последовательность бесконечная.
Бесконечные интервалы
Некоторые интервалы по определению будут бесконечными, даже имея начальный и конечный итератор одинаковых типов.
// бесконечный интервал нулей
class zeros : public range_facade<zeros>
{
friend range_core_access;
struct impl
{
bool sentinel;
int current() const { return 0; }
void next() {}
bool equal(impl that) const
{ return sentinel == that.sentinel; }
};
// begin() и end() работают через range_facade
// как begin_impl и end_impl. И они будут одного типа
impl begin_impl() const { return {false}; }
impl end_impl() const { return {true}; }
};
// нули моделируют концепцию Range
CONCEPT_ASSERT(Range<zeros>());
int main()
{
// бесконечность
for_each(zeros(), [](int i) {/*...*/});
}
Хотелось бы сразу отлавливать подобные ошибки, но, очевидно, бинарная функция DenotesInfiniteSequence с этим не справится. Для нулей типы BeginType и EndType будут одинаковыми, так что DenotesInfiniteSequence вернёт false.
Поэтому надо сконструировать унарную функцию типов IsInfinite, принимающую тип интервала.
// сообщить о том, будет ли Iterable бесконечным
template<typename Iterable>
struct is_infinite
: std::integral_constant<bool, true-or-false>
{};
Её можно использовать для определения концепции FiniteIterable
// текущий вариант синтаксиса Concept Lite
template<typename T>
concept bool FiniteIterable =
Iterable<T> && !is_infinite<T>::value;
Каждый FiniteIterable является Iterable. Наблюдается параллельная иерархия уточнений:

И все эти концепции, по аналогии с Range, не нужно определять в коде. Конечность ортогональна иерархии Iterable, и её можно опрашивать отдельно.
Но почему FiniteIterable, а не InfiniteIterable? Всё дело в алгоритмах и их требованиях. Нет алгоритмов, которые требуют, чтобы их аргументы интервалов были бесконечными. Поэтому бесполезно было бы иметь возможность писать InfiniteIterable. А вот алгоритм вроде lower_bound хотел бы, чтобы интервал был конечным. От этого и FiniteIterable.
Значит, все итераторы моделируют FiniteIterable по умолчанию, и тип должен как-то научиться быть бесконечным. Как? Можно специализировать is_infinite. К счастью, инструменты для создания инкременторов и интервалов принимают опциональный параметр IsInfinite, поэтому это сделать легко. Вот как теперь выглядит класс zeroes:
// бесконечные нули
class zeros : public range_facade<zeros, true>
{ // ... IsInfinite ...................^^^^
// ... тут всё, как было ...
};
// zeros – это Range, но он не Finite
CONCEPT_ASSERT(Range<zeros>());
CONCEPT_ASSERT(!FiniteIterable<zeros>());
Добавив концепцию FiniteIterable мы даём алгоритмам, которым требуется конечность, возможность проверить это на этапе компиляции.
Возможно бесконечные интервалы
Теперь нам надо разделить интервалы на категории. По идее, либо он бесконечный, либо конечный – не так ли? Вообще-то, нет. Возьмём istream. Он может быть конечным, может не быть. Обычно поток прекращается, но иногда…
Ситуация сложная. Нужно ли запрещать передачу istream в алгоритм только из-за того, что он может быть бесконечным?
Считаем несчётное
С бесконечными интервалами есть такая трудность: у всех итераторов и всех инкременторов есть связанный с ними difference_type. Александр Степанов пишет об этом:
DistanceType возвращает целочисленный тип, достаточно большой для измерения любой последовательности применений successor, допустимых для типа.
Получается, что нам требуется целый тип бесконечного размера. Есть ли решение этой задачи?
- В С++ требуется bigint – целый тип с бесконечной точностью. В других языках он есть. С++ – прекрасный язык для создания библиотек, и на эту тему просто просится библиотека. Если бы был такой тип, его можно было бы взять в качестве difference_type.
- Бесконечные интервалы могут использовать safe_int в качестве difference_type. safe_int ведёт себя, как int, но может представлять бесконечность. Он не переполняется. Две самые сложные проблемы с переполнением difference_type – неопределённое поведение и невозможность сказать постфактум, что пошло не так. С safe_int можно избежать неопределённостей и впоследствии узнать, что случилось.
- Можно предложить альтернативную реализацию safe_int, в которой он выбрасывает исключение при переполнении.
- Ещё можно было бы посмотреть, где библиотека использует difference_type и дать возможность пользователю указать, что там будет использоваться другой тип. Например, API алгоритма вычисления расстояния может принимать интервал и опциональное начальное значение. Она бы по умолчанию работала с difference_type{0}, но если бы вы передавали ей bigint, то работала бы с ним по-другому, медленнее, но безопаснее.
- Можно игнорировать проблему. А те, кто заботится о переполнении, могут использовать адаптер счётного интервала (https://github.com/ericniebler/range-v3/blob/master/include/range/v3/view/counted.hpp), чтобы удостовериться в том, что итерации остановятся перед переполнением difference_type.
- Что-то ещё, что не пришло мне в голову.
Мне, конечно, не нравится всё, что замедляет работу алгоритмов, поэтому std::ptrdiff_t вполне можно оставить в качестве difference_type по умолчанию. Кроме этого, нужно разработать интерфейсы интервалов так, чтобы дать пользователям возможность задавать другой difference_type, если они заботятся о переполнении. Поэтому мне нравятся варианты 4 и 5. Другие библиотечные типы вроде bigint или safe_int с определёнными ограничениями было бы неплохо иметь возможность применить – если бы пользователь мог указать их использование, меняя скорость на безопасность, когда ему это нужно.
Итог, и что делать далее
Возможно, читая предыдущие посты, вы были излишне оптимистичны: всё вроде бы начинало получаться, а теперь вы запутались. Но мне кажется, что мы неплохо продвинулись, по сравнению с тем, откуда начинали. Я описал 5 проблем с интервалами, использующими пару итераторов. Новая концепция инкременторов решает 3 из них, 4-ю проблему (бесконечные интервалы) теоретически можно решить улучшением этой концепции. И есть несколько вариантов работы с 5-й (переполнением). По крайней мере, начало положено.
Некоторые спрашивают – планирую ли я донести свои идеи до комитета по стандартизации С++. Разумеется. Когда мы получим поддержку концепций в языке, появится потребность в концептуализированной версии STL, возможно, работающей в другом пространстве имён.
А пока я займусь обсуждением вопроса в рассылке SG9 (Ranges) (http://www.open-std.org/mailman/listinfo/ranges). Этот спорный вопрос наверняка сможет породить новые идеи. Интересующихся призываю присоединяться к обсуждению.
Автор донес свои идеи до комитета и сейчас занимается их реализацией.
Другие статьи цикла
Интервалы в С++, часть 1: Интервалы с ограничителями
Интервалы в С++, часть 2: Бесконечные интервалы
Интервалы в С++, часть 3: представляем инкременторы (Iterable)


nickolaym
В копилку идей, как работать с бисекцией бесконечных интервалов — т.е. lower_bound(begin(iota), end(iota), xz)
Нужно вычислять точку разбиения не просто как start+distance(start,finish)/2, а
В принципе, можно надругаться над difference_type, чтобы он содержал не только конечные числа, [0..oo), возможно, (-oo..0), но и бесконечные [oo-0, oo-1, oo-2, ..oo), ну и в минус-бесконечность (..., oo-(-3), oo-(-2), oo-(-1))
так, что операция деления пополам давала конечное: (oo-N)/2 = N; (oo-(-N))/2 = 0 ибо нефиг.
Всего-то навсего, один бит признака «вычитание из бесконечности».
В принципе, если нам не жалко разрядности, можем взять long long и зарезервировать оттуда 1 бит. Ну, будет у нас 62-битный диапазон доступных чисел.
Либо big int плюс булев флажок.