Несмотря на то, что описание данных с помощью графов практикуется еще с позапрошлого столетия, использование их в решении повседневных задач по анализу данных лишь набирает обороты. Хотя основное внимание уделяется, как водится, графовым эмбеддингам и сверточным сетям, маленькие шаги предпринимаются и в алгоритмах по поиску аномалий или антифроде. Основная обзорная статья, на которую ссылается большинство специалистов в своих в докладах и публикациях, — Graph based anomaly detection and description: a survey от авторов Leman Akoglu, Hanghang Tong, Danai Koutra (Akoglu, 2015). Мы в CleverDATA решили рассказать Хабру об этом практически единственном материале по теме и предлагаем вашему вниманию его саммари.
 Первый граф Российского царства Борис Петрович Шереметев. Аномалий не обнаружено.
Первый граф Российского царства Борис Петрович Шереметев. Аномалий не обнаружено.
Во вступлении авторы отвечают на вопрос: «В чем же преимущества поиска аномалий с использованием теории графов?»:
От себя хочется добавить, что, хотя для некоторых типов данных переход к графовому представлению данных требует тщательного задания принципов такого перехода и требует определенных ухищрений, для многих типов данных (социальные сети, банковские операции, компьютерные сети) такое представление естественно и требует соответствующих методов работы с ним.
Таким образом, перспективность использования теории графов для поиска аномалий обоснована. Перейдем к описанию самих методов.
В статье графовые методы для поиска аномалий делятся в зависимости от того, к статическим или динамическим графам они применяются. Авторы делят статические графы на две группы: обычные и те, для которых узлам и ребрам соответствуют какие-либо свойства. В рамках каждой подгруппы авторы подразделяют подходы на структурные и на основанный на поиске сообществ.
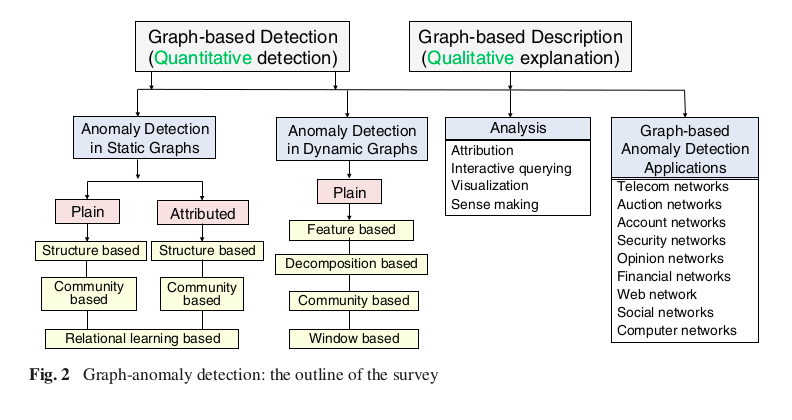
Для простых графов выделяют три направления структурных подходов: поиск аномалий на основе признаков узлов, диад узлов, триад, эгонетов (egonet), на основе сообществ и на основе метрик близости (proximity): pagerank, personalized pagerank, simrank. При этом предлагается для решения задачи поиска аномалий на графе использовать обычные алгоритмы (например, Isolation Forest, или если есть разметка, то стандартные классификаторы), но на основе графовых признаков.
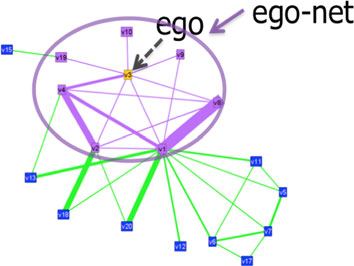 Пример Эгонета
Пример Эгонета
Отдельно описывается подход с признаками эгонетов — подграфов, включающих целевой узел, и его ближайших соседей. Авторы, ссылаясь на статью 2010 года (Akoglu, 2010) (в статье будет очень много таких ссылок, гиперссылки на некоторые я дал в тексте, но более подробные ссылки, например, с указанием страниц, вы найдёте в списке литературы в конце этой статьи), предлагают искать характерные для графа паттерны эгонетов с выраженной зависимостью между характеристиками, а эгонеты, не соответствующие этим паттернам, считать аномальными, и, таким образом, считать аномальными их центральные узлы. Поскольку всевозможных показателей на основе эгонетов может быть много, авторы в этой же статье обосновывают свой выбор подгруппы таких показателей, наилучшим образом отражающие свойства графа (например, число треугольников, общий вес ребер). Расстояние между паттернами и между эгонетом и паттерном предлагается измерять, как отклонение характеристики этого эгонета от характерной зависимости, соответствующей паттерну.
Другая ветка поиска аномалий на основе графов основывается на обнаружении тесно связанных групп или сообществ. Аномальными предлагается считать узлы или ребра, которые не принадлежат ни к какому сообществу или принадлежат сразу нескольким.
Также авторы описывают и другие подходы:
Основная идея таких подходов заключается в последовательном решении двух задач: поиск аномальных подграфов с точки зрения структуры и поиск в рамках этого подмножества аномальных подграфов с точки зрения свойств узлов и/или ребер. Решение этой задачи авторы рассматривают как поиск редких элементов в множестве, сводя ее таким образом к задаче обратной по отношению к поиску элементов, которые чаще всего встречаются в графе, и, таким образом, являются для него наиболее характерными (лучше всего «сжимают» граф).
Также рассматривается проблема наличия у узлов множества характеристик различных модальностей. Предлагается всем условно нормальным значениям ставить в соответствие единственное значение категориальной переменной, а для выбросов ставить в соответствие значение единственного показателя аномальности, например, на основании метрических методов обнаружения аномалий: kNN, LOF.
Также перечисляются и другие возможности: SAX (Symbolic Aggregate approXimation) (Lin et al., 2003), MDL-binning (Minimum description length) (Kontkanen and Myllymki, 2007) и дискретизация по минимуму энтропии (Fayyad and Irani, 1993). Авторы этой статьи (Eberlie and Holder, 2007) иначе подходят к определению аномалии в графовых данных, считая аномальными те подграфы, которые похожи по отношению к условно нормальному графу в определенных пределах. Такой подход авторы обосновывают тем, что самые успешные мошенники будут стараться максимально подражать реальности. Они также предлагают учитывать стоимость модификации показателя и формулируют показатели аномальности с учетом этой стоимости (чем меньше стоимость, тем более аномальным является показатель).
Поиск аномалий для графов с атрибутированными узлами рассматривается и в основанный на поиске сообществ парадигме. Предлагается подразделять графы на сообщества. Далее, в рамках каждого сообщества, искать аномалии по атрибутам. Например, курильщик в команде по бейcболу. Курильщик не является аномалией для общества в целом, но в своем сообществе является. Другой подход (Muller, 2013) основывается на выборе пользователем (аналитиком) набора узлов, для которых далее определяется подпространство показателей, схожих для них. А аномалиями в таком подходе являются узлы, которые структурно принадлежат к кластеру этих узлов, но в выбранном подпространстве показателей находятся далеко от них.
Отдельно рассматриваются методы semi-supervised, в предположении, что какая-то часть узлов размечена как нормальные и аномальные, а остальные узлы можно классифицировать, используя соответствующие методики, а в самом простом случае им можно присваивать метки соседних с ними узлов. Перечисляются основные подходы: iterative classification algorithm, gibbs sampling (подробнее про эти подходы пишут здесь), loopy belief propagation, weighted-vote relational network classifier.
Для динамического графа, который представляет собой упорядоченную во времени последовательность статических графов, основной подход осуществляется следующим образом:
В качестве мер расстояния предлагаются:
В статье от Bunke et al. (2006) авторы предлагают считать расстояние не только между последовательно идущими графами, но вообще между всеми графами в последовательности, и потом применять многомерное шкалирование, переводя графы в двумерное пространство. Далее выбросы ищутся в этом двумерном пространстве.
Описан также следующий способ работы с динамическими графами (Box and Jenkins, 1990): графу ставится в соответствие некое число (расчетный показатель) и далее применяются стандартные методы поиска аномалий во временных рядах. Например, расхождения с моделью ARIMA.
В статье Akoglu and Faloutsos (2010) авторы осуществляют следующую последовательность операций:
Матричное разложение используется также и в статье Rossi (2013):
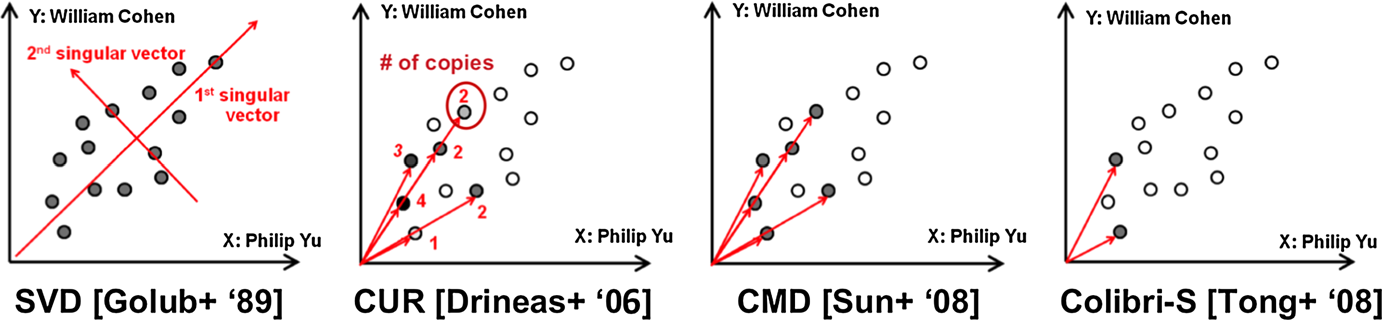
Отдельно хочется отметить приведенные авторами методы аппроксимации матриц — альтернативные по отношению к давно известным SVD, PCA, NMF: CUR (Drineas et al., 2006), CMD (Sun et al. 2007b) и Colibri (Tong et al. 2008). Основным преимуществом этих методов является интерпретируемость, поскольку в отличии от SVD, переводящего точки в другое пространство, эти методы оставляют пространство нетронутым, лишь сэмплируя точки из него. Наиболее простым из них является CUR, у которого авторы отмечают два недостатка: в нем точки выбираются из матрицы с повторением. В CMD удается убрать этот недостаток, однако как и в CUR, этому методу присуща линейная избыточность, которую удается избежать авторам алгоритма Colibri. Хотя методы были изобретены именно для решения задач поиска аномалий в графах методами матричной аппроксимации, их использование может быть перспективным и для других задач.
В задачах, обсуждаемых в этом обзоре, эти подходы применяются по следующему принципу: производится аппроксимация и оценивается, насколько различные столбцы/строки отличаются у аппроксимированной матрицы от изначальной. Также авторы отмечают метод NrMF (Tong and Lin 2011), модификация NMF, в котором ограничение на неотрицательность накладывается на матрицу остатков R, поскольку именно в ней сосредоточена основная информация по отличию апроксимации от изначальной матрицы, а отрицательные значения в таком случае было бы сложно интерпретировать. Тем не менее, до конца не ясно, почему нельзя аналогичным образом использовать SVD для декомпозиции, последующей реконструкции и последующим расчетом отличия от изначальной матрицы.
При анализе результатов может возникнуть задача определить узлы, связанные с аномальными. Так, например, как аномальный может быть определен узел, который подвергся DDoS-атаке, в то время как атакующие узлы не определены. Или как аномальные могут быть определены члены какой-то группировки, в то время как люди, руководящие ими, не определены как аномальные. Для решения этой задачи авторы предлагают несколько подходов, основной идеей которых является выделение подграфа из полного графа, который содержит аномальные узлы и узлы, лучше всего их связывающие.
Авторы описывают кейсы, где применялись методы обнаружения аномалий в графах.
Телекоммуникации. Целью являются люди, пользующиеся услугами бесплатно. Cortes et al. (2002) искали подграфы, тесно связанные с ключевым узлом по параметрам числа и продолжительности звонков. Наблюдения, которые авторы обнаружили: фродовые аккаунты оказались связаны, то есть нарушители или сами звонили друг другу, или звонили на одни и те же телефоны. Второе наблюдение — нарушителей можно обнаружить по схожести их подграфов, определенных предложенным образом.
Онлайн-аукцион. Нарушители создают себе фейковые аккаунты и накручивают им рейтинги. Их не получается отследить по обычным агрегатным показателям, но возможно увидеть по графу. Аккаунты нарушителей более связаны с фейковыми аккаунтами, чем с хорошими аккаунтами. Фейки связаны примерно в равной степени с аккаунтами нарушителей и с хорошими. Последние в основном связаны с подобными себе аккаунтами. Pandit et al. (2007) решают эту задачу через приведение к реляционным марковским сетям (relational markov networks) и далее классифицируют узлы через Loopy Belief Propagation (метки класса итеративно распространяются по графу).
Транзакции. McGlohon et al. (2009) решают эту задачу через реляционную (relational) классификацию в предположении, что нарушители будут близко расположены друг к другу. То есть аналогично подходу из предыдущего примера.
Брокеры, которые жульничают с ценными бумагами. Здесь Neville et al. (2005) анализируют мультимодальный граф, выделяя подграфы, включающие человека под подозрением, его коллег, фирмы, с которыми он связан и т. п. Они рассчитывают агрегированные атрибуты и приписывают их центральному узлу. Далее используют реляционные вероятностные деревья (relational probability trees (Neville et al. 2003)) для реляционной классификации.
Поиск фейковых постов на форумах, дающих заведомо ложную информацию. Авторы описывают несколько подходов, с использованием признакового описания, анализа текста и графовых методов. Графовые методы, использованные Wang et al. (2011a), применялись для ситуации, когда в задаче присутствуют обзоры какого-то товара. В предложенном ими алгоритме предлагалось присваивать рецензентам показатели «степени доверия им», их обзорам «достоверности» и товарам — показатели «надежности». Все эти показатели взаимосвязаны. Так, насколько можно доверять рецензенту, зависит от того, насколько у него достоверные обзоры. Надежность товаров зависит от степени доверия рецензентам, которые его описывают, а достоверность обзоров зависит от надежности товара, по которым они пишутся, и от доверия их авторам. Предлагаемый алгоритм сначала их случайно инициализирует, а затем итеративно улучшает оценку.
Трейдинг. Мошенники сначала совершают большое число транзакций друг с другом по какому-то типу акций, увеличивая их привлекательность, а затем, когда акции повышаются в цене, распродают их другим трейдерам. Оба этих последовательных инцидента можно отследить по графовым данным. В первом случае будет выделяться подграф, где нет никаких внешних транзакций (именуется «черная дыра»), а через временной промежуток этот же подграф преобразуется к подграфу, в котором сильно преобладают транзакции из подграфа в другую часть графа (именуется «вулкан»). Авторы ссылаются на работу Li et al. (2010).
Веб-ресурсы. Одним из первых подходов для борьбы с «плохими» веб-сайтами предлагалось распространение показателей «надежности» и «ненадежности» ресурсов. Если есть ссылка с одной страницы на другую, то для последней это увеличивает ее статус надежной. Если страница указывает на другую страницу, для которой известно, что она спам, то это снижает надежность изначальной страницы. Упоминается алгоритм TrustRank (Gyongyi et al., 2004) — модификация PageRank для борьбы с веб-спамом. Для него требуется, чтобы изначально эксперты разметили часть сайтов, как надежные. Эти показатели далее распространяются по графу, постепенно затухая. Anti-TrustRank (Krishnan and Raj, 2006) следует этому же принципу, но с распространением показателей ненадежности от размеченных заведомо ненадежных сайтов. У обоих методов есть недостаток, что надежность делится по числу дочерних узлов. Benczur et al. (2005) предлагают совершенно иной подход: анализировать PageRank узла и соседних с ним. Распределение PageRank таких подграфов должно подчиняться некому степенному закону. Для тех же узлов, для которых распределение PageRank их соседей выбивается из этого закона, присваивается штраф. В работе (Castillo et al., 2007) предлагается сначала обучать классификатор на известных надежных и ненадежных страницах, а затем «размывать» результат скоринга остальных веб-сайтов по графу.
Социальные сети. Для обнаружения постов мошенников в социальных сетях (для увеличения числа лайков, для перенаправления на вредоносную страницу или на анкетирование) описываются подходы на основе обычных классификаторов, но с учетом графовых признаков: длина распространения «плохого» поста по графу, число лайков и комментов других пользователей по посту, схожесть сообщений, распространяющих пост пользователей, степень узла пользователя, написавшего пост.
Атаки в компьютерных сетях. Sun et al. (2008) успешно применяют для решения этой задачи матричное разложение (CMD). Ding et al. (2012) используют подход основанный на поиске сообществ, выделяя в качестве подозрительных узлы-мосты между сообществами.
Теория графов до недавнего времени соприкасалась с машинным обучением только для социальных сетей, где по-другому совсем нельзя. Сейчас применение теории графов для решения классических ML-задач постепенно развивается, но пока медленно. В основном потому, что задач, где целесообразно переходить к графовому представлению, все равно мало. Сейчас на мировых конференциях угадывается тренд постепенного развития этой области, но в основном теории, а не практики. Библиотеки по работе с графами достаточно ограничены и плохо развиваются. Поиск аномалий — еще более редкая задача, поскольку осуществляется без разметки, и качество обнаружения аномалий можно оценить лишь экспертным путем. Во многих задачах переход к графовому описанию не целесообразен.
Если интересно почитать про стандартные методы обнаружения аномалий, то у я уже писал про это год назад на Хабре в этой статье.
Если вас интересует тема, то, чтобы получить больше информации, обязательно нужно идти в слак ODS (OpenDataScience), в каналы #network_analysis и #class_cs224w, смотреть курс Стэнфорда cs224w.
Еще недавно был прочитан курс по Knowledge Graphs. Ну и, конечно, нужно прочитать саму статью Graph based anomaly detection and description: a survey от авторов Leman Akoglu, Hanghang Tong, Danai Koutra (Akoglu, 2015), о которой идет речь в этом посте. Я перевел ее не всю, а только те фрагменты, которые счел важными, и понял в какой-то степени. Большинство авторов ссылаются именно на эту статью, потому что больше обзоров такого уровня и широты по теме нет. По крайней мере, я не нашел таких.
Да, наша команда CleverDATA не только пишет и переводит статьи. Большую часть времени мы посвящаем решению интересных и разнообразных практических задач, для чего используем не только теорию графов, но и множество методов машинного и глубокого обучения.

Во вступлении авторы отвечают на вопрос: «В чем же преимущества поиска аномалий с использованием теории графов?»:
- большая часть данных, с которыми мы сталкиваемся, взаимосвязана, и необходимо использовать сущности, способные это учитывать;
- графы крайне удобны и понятны для человека;
- аномалии, как правило, связаны друг с другом, особенно при рассмотрении фрода;
- мошенникам сложнее адаптировать поведение под такие методы, поскольку у них отсутствует видение графа в целом и, соответственно, понимание, как адаптировать свою стратегию в соответствии с возможными действиями антифрод систем.
От себя хочется добавить, что, хотя для некоторых типов данных переход к графовому представлению данных требует тщательного задания принципов такого перехода и требует определенных ухищрений, для многих типов данных (социальные сети, банковские операции, компьютерные сети) такое представление естественно и требует соответствующих методов работы с ним.
Таким образом, перспективность использования теории графов для поиска аномалий обоснована. Перейдем к описанию самих методов.
В статье графовые методы для поиска аномалий делятся в зависимости от того, к статическим или динамическим графам они применяются. Авторы делят статические графы на две группы: обычные и те, для которых узлам и ребрам соответствуют какие-либо свойства. В рамках каждой подгруппы авторы подразделяют подходы на структурные и на основанный на поиске сообществ.

Поиск аномалий в графах без свойств, приписанных вершинам и/или ребрам
Для простых графов выделяют три направления структурных подходов: поиск аномалий на основе признаков узлов, диад узлов, триад, эгонетов (egonet), на основе сообществ и на основе метрик близости (proximity): pagerank, personalized pagerank, simrank. При этом предлагается для решения задачи поиска аномалий на графе использовать обычные алгоритмы (например, Isolation Forest, или если есть разметка, то стандартные классификаторы), но на основе графовых признаков.

Отдельно описывается подход с признаками эгонетов — подграфов, включающих целевой узел, и его ближайших соседей. Авторы, ссылаясь на статью 2010 года (Akoglu, 2010) (в статье будет очень много таких ссылок, гиперссылки на некоторые я дал в тексте, но более подробные ссылки, например, с указанием страниц, вы найдёте в списке литературы в конце этой статьи), предлагают искать характерные для графа паттерны эгонетов с выраженной зависимостью между характеристиками, а эгонеты, не соответствующие этим паттернам, считать аномальными, и, таким образом, считать аномальными их центральные узлы. Поскольку всевозможных показателей на основе эгонетов может быть много, авторы в этой же статье обосновывают свой выбор подгруппы таких показателей, наилучшим образом отражающие свойства графа (например, число треугольников, общий вес ребер). Расстояние между паттернами и между эгонетом и паттерном предлагается измерять, как отклонение характеристики этого эгонета от характерной зависимости, соответствующей паттерну.
Другая ветка поиска аномалий на основе графов основывается на обнаружении тесно связанных групп или сообществ. Аномальными предлагается считать узлы или ребра, которые не принадлежат ни к какому сообществу или принадлежат сразу нескольким.
Также авторы описывают и другие подходы:
- кластеризация узлов на основании сходства их ближайшего окружения; предлагается реорганизация матрицы смежности для получения более плотных и менее плотных блоков (Chakrabarti 2004; Rissanen, 1999);
- матричная факторизация; предлагается аналог Non-negative matrix factorization (NMF) (Tong and Lin 2011).
Поиск аномалий в графах с узлами и/или ребрами, обладающими свойствами
Основная идея таких подходов заключается в последовательном решении двух задач: поиск аномальных подграфов с точки зрения структуры и поиск в рамках этого подмножества аномальных подграфов с точки зрения свойств узлов и/или ребер. Решение этой задачи авторы рассматривают как поиск редких элементов в множестве, сводя ее таким образом к задаче обратной по отношению к поиску элементов, которые чаще всего встречаются в графе, и, таким образом, являются для него наиболее характерными (лучше всего «сжимают» граф).
Также рассматривается проблема наличия у узлов множества характеристик различных модальностей. Предлагается всем условно нормальным значениям ставить в соответствие единственное значение категориальной переменной, а для выбросов ставить в соответствие значение единственного показателя аномальности, например, на основании метрических методов обнаружения аномалий: kNN, LOF.
Также перечисляются и другие возможности: SAX (Symbolic Aggregate approXimation) (Lin et al., 2003), MDL-binning (Minimum description length) (Kontkanen and Myllymki, 2007) и дискретизация по минимуму энтропии (Fayyad and Irani, 1993). Авторы этой статьи (Eberlie and Holder, 2007) иначе подходят к определению аномалии в графовых данных, считая аномальными те подграфы, которые похожи по отношению к условно нормальному графу в определенных пределах. Такой подход авторы обосновывают тем, что самые успешные мошенники будут стараться максимально подражать реальности. Они также предлагают учитывать стоимость модификации показателя и формулируют показатели аномальности с учетом этой стоимости (чем меньше стоимость, тем более аномальным является показатель).
Поиск аномалий для графов с атрибутированными узлами рассматривается и в основанный на поиске сообществ парадигме. Предлагается подразделять графы на сообщества. Далее, в рамках каждого сообщества, искать аномалии по атрибутам. Например, курильщик в команде по бейcболу. Курильщик не является аномалией для общества в целом, но в своем сообществе является. Другой подход (Muller, 2013) основывается на выборе пользователем (аналитиком) набора узлов, для которых далее определяется подпространство показателей, схожих для них. А аномалиями в таком подходе являются узлы, которые структурно принадлежат к кластеру этих узлов, но в выбранном подпространстве показателей находятся далеко от них.
Отдельно рассматриваются методы semi-supervised, в предположении, что какая-то часть узлов размечена как нормальные и аномальные, а остальные узлы можно классифицировать, используя соответствующие методики, а в самом простом случае им можно присваивать метки соседних с ними узлов. Перечисляются основные подходы: iterative classification algorithm, gibbs sampling (подробнее про эти подходы пишут здесь), loopy belief propagation, weighted-vote relational network classifier.
Поиск аномалий в динамическом графе
Для динамического графа, который представляет собой упорядоченную во времени последовательность статических графов, основной подход осуществляется следующим образом:
- выделяется некоторое сжатие или интегральная характеристика каждого статического графа;
- вычисляется расстояние последовательно идущих графов;
- аномальными принимаются те графы, для которых расстояние выше порога.
В качестве мер расстояния предлагаются:
- maximum common subgraph (MCS) distance;
- error correcting graph matching distance, то есть расстояние, измеряющее, сколько шагов нужно сделать, чтобы из одного графа сделать другой;
- graph edit distance (GED), то же, что и предыдущее, но возможны лишь топологические изменения;
- расстояния между матрицами смежности (например, Хэмминга);
- различные расстояния на основе весов ребер;
- расстояния между спектральным представлением графов (распределениями собственных векторов);
- описывается также и более экзотическая мера: эвклидово расстояние между перроновскими собственными векторами графа.
В статье от Bunke et al. (2006) авторы предлагают считать расстояние не только между последовательно идущими графами, но вообще между всеми графами в последовательности, и потом применять многомерное шкалирование, переводя графы в двумерное пространство. Далее выбросы ищутся в этом двумерном пространстве.
Описан также следующий способ работы с динамическими графами (Box and Jenkins, 1990): графу ставится в соответствие некое число (расчетный показатель) и далее применяются стандартные методы поиска аномалий во временных рядах. Например, расхождения с моделью ARIMA.
В статье Akoglu and Faloutsos (2010) авторы осуществляют следующую последовательность операций:
- выделяют для каждого узла графа для каждого момента времени F-признаков;
- для каждого признака с временным окном W считают корреляционные матрицы между узлами;
- выделяют собственные векторы и далее рассматривают лишь первый собственный вектор;
- параллельно выделяют «типичное» поведение собственных векторов корреляционной матрицы (для этого делается еще одно SVD-разложение над матрицей изменения всех собственных векторов корреляционной матрицы во времени);
- сравнивают (через косинусное произведение) с реальным поведением этого вектора, получая таким образом показатель аномальности рассматриваемого временного окна.
Матричное разложение используется также и в статье Rossi (2013):
- аналогично предыдущему подходу выделяется по F-признаков на узел на каждый временной промежуток;
- для каждого временного промежутка производится NMF-разложение, при котором каждому узлу ставится в соответствие роль;
- далее мониторится изменение ролей каждого узла.
Матричное разложение для интерпретации результатов
Отдельно хочется отметить приведенные авторами методы аппроксимации матриц — альтернативные по отношению к давно известным SVD, PCA, NMF: CUR (Drineas et al., 2006), CMD (Sun et al. 2007b) и Colibri (Tong et al. 2008). Основным преимуществом этих методов является интерпретируемость, поскольку в отличии от SVD, переводящего точки в другое пространство, эти методы оставляют пространство нетронутым, лишь сэмплируя точки из него. Наиболее простым из них является CUR, у которого авторы отмечают два недостатка: в нем точки выбираются из матрицы с повторением. В CMD удается убрать этот недостаток, однако как и в CUR, этому методу присуща линейная избыточность, которую удается избежать авторам алгоритма Colibri. Хотя методы были изобретены именно для решения задач поиска аномалий в графах методами матричной аппроксимации, их использование может быть перспективным и для других задач.
В задачах, обсуждаемых в этом обзоре, эти подходы применяются по следующему принципу: производится аппроксимация и оценивается, насколько различные столбцы/строки отличаются у аппроксимированной матрицы от изначальной. Также авторы отмечают метод NrMF (Tong and Lin 2011), модификация NMF, в котором ограничение на неотрицательность накладывается на матрицу остатков R, поскольку именно в ней сосредоточена основная информация по отличию апроксимации от изначальной матрицы, а отрицательные значения в таком случае было бы сложно интерпретировать. Тем не менее, до конца не ясно, почему нельзя аналогичным образом использовать SVD для декомпозиции, последующей реконструкции и последующим расчетом отличия от изначальной матрицы.

Определение узлов, связывающих аномальные
При анализе результатов может возникнуть задача определить узлы, связанные с аномальными. Так, например, как аномальный может быть определен узел, который подвергся DDoS-атаке, в то время как атакующие узлы не определены. Или как аномальные могут быть определены члены какой-то группировки, в то время как люди, руководящие ими, не определены как аномальные. Для решения этой задачи авторы предлагают несколько подходов, основной идеей которых является выделение подграфа из полного графа, который содержит аномальные узлы и узлы, лучше всего их связывающие.
- Определение связного подграфа (connection subgraph) (Faloutsos et al., 2004). Проблему предлагается решать в терминах электротехники, присваивая одному узлу положительный потенциал, а другим узлам — нулевой, и смотреть, как будет «течь ток» между ними, если присвоить ребрам некое сопротивление.
- Center-Piece Subgraphs (CePS) (Tong and Faloutsos, 2006). В отличие от предыдущего метода предпринимается попытка выделить лишь k-узлов из всех аномальных, поскольку совершенно не обязательно все узлы заданы. При этом k необходимо задавать.
- Dot2Dot (Akoglu et al., 2013b; Chau et al., 2012). В этом подходе авторы решают задачу группировки выбранных узлов и уже далее выделяют узлы, их связывающие.
Примеры поиска аномалий в различных сферах
Авторы описывают кейсы, где применялись методы обнаружения аномалий в графах.
Телекоммуникации. Целью являются люди, пользующиеся услугами бесплатно. Cortes et al. (2002) искали подграфы, тесно связанные с ключевым узлом по параметрам числа и продолжительности звонков. Наблюдения, которые авторы обнаружили: фродовые аккаунты оказались связаны, то есть нарушители или сами звонили друг другу, или звонили на одни и те же телефоны. Второе наблюдение — нарушителей можно обнаружить по схожести их подграфов, определенных предложенным образом.
Онлайн-аукцион. Нарушители создают себе фейковые аккаунты и накручивают им рейтинги. Их не получается отследить по обычным агрегатным показателям, но возможно увидеть по графу. Аккаунты нарушителей более связаны с фейковыми аккаунтами, чем с хорошими аккаунтами. Фейки связаны примерно в равной степени с аккаунтами нарушителей и с хорошими. Последние в основном связаны с подобными себе аккаунтами. Pandit et al. (2007) решают эту задачу через приведение к реляционным марковским сетям (relational markov networks) и далее классифицируют узлы через Loopy Belief Propagation (метки класса итеративно распространяются по графу).
Транзакции. McGlohon et al. (2009) решают эту задачу через реляционную (relational) классификацию в предположении, что нарушители будут близко расположены друг к другу. То есть аналогично подходу из предыдущего примера.
Брокеры, которые жульничают с ценными бумагами. Здесь Neville et al. (2005) анализируют мультимодальный граф, выделяя подграфы, включающие человека под подозрением, его коллег, фирмы, с которыми он связан и т. п. Они рассчитывают агрегированные атрибуты и приписывают их центральному узлу. Далее используют реляционные вероятностные деревья (relational probability trees (Neville et al. 2003)) для реляционной классификации.
Поиск фейковых постов на форумах, дающих заведомо ложную информацию. Авторы описывают несколько подходов, с использованием признакового описания, анализа текста и графовых методов. Графовые методы, использованные Wang et al. (2011a), применялись для ситуации, когда в задаче присутствуют обзоры какого-то товара. В предложенном ими алгоритме предлагалось присваивать рецензентам показатели «степени доверия им», их обзорам «достоверности» и товарам — показатели «надежности». Все эти показатели взаимосвязаны. Так, насколько можно доверять рецензенту, зависит от того, насколько у него достоверные обзоры. Надежность товаров зависит от степени доверия рецензентам, которые его описывают, а достоверность обзоров зависит от надежности товара, по которым они пишутся, и от доверия их авторам. Предлагаемый алгоритм сначала их случайно инициализирует, а затем итеративно улучшает оценку.
Трейдинг. Мошенники сначала совершают большое число транзакций друг с другом по какому-то типу акций, увеличивая их привлекательность, а затем, когда акции повышаются в цене, распродают их другим трейдерам. Оба этих последовательных инцидента можно отследить по графовым данным. В первом случае будет выделяться подграф, где нет никаких внешних транзакций (именуется «черная дыра»), а через временной промежуток этот же подграф преобразуется к подграфу, в котором сильно преобладают транзакции из подграфа в другую часть графа (именуется «вулкан»). Авторы ссылаются на работу Li et al. (2010).
Веб-ресурсы. Одним из первых подходов для борьбы с «плохими» веб-сайтами предлагалось распространение показателей «надежности» и «ненадежности» ресурсов. Если есть ссылка с одной страницы на другую, то для последней это увеличивает ее статус надежной. Если страница указывает на другую страницу, для которой известно, что она спам, то это снижает надежность изначальной страницы. Упоминается алгоритм TrustRank (Gyongyi et al., 2004) — модификация PageRank для борьбы с веб-спамом. Для него требуется, чтобы изначально эксперты разметили часть сайтов, как надежные. Эти показатели далее распространяются по графу, постепенно затухая. Anti-TrustRank (Krishnan and Raj, 2006) следует этому же принципу, но с распространением показателей ненадежности от размеченных заведомо ненадежных сайтов. У обоих методов есть недостаток, что надежность делится по числу дочерних узлов. Benczur et al. (2005) предлагают совершенно иной подход: анализировать PageRank узла и соседних с ним. Распределение PageRank таких подграфов должно подчиняться некому степенному закону. Для тех же узлов, для которых распределение PageRank их соседей выбивается из этого закона, присваивается штраф. В работе (Castillo et al., 2007) предлагается сначала обучать классификатор на известных надежных и ненадежных страницах, а затем «размывать» результат скоринга остальных веб-сайтов по графу.
Социальные сети. Для обнаружения постов мошенников в социальных сетях (для увеличения числа лайков, для перенаправления на вредоносную страницу или на анкетирование) описываются подходы на основе обычных классификаторов, но с учетом графовых признаков: длина распространения «плохого» поста по графу, число лайков и комментов других пользователей по посту, схожесть сообщений, распространяющих пост пользователей, степень узла пользователя, написавшего пост.
Атаки в компьютерных сетях. Sun et al. (2008) успешно применяют для решения этой задачи матричное разложение (CMD). Ding et al. (2012) используют подход основанный на поиске сообществ, выделяя в качестве подозрительных узлы-мосты между сообществами.
Заключение
Теория графов до недавнего времени соприкасалась с машинным обучением только для социальных сетей, где по-другому совсем нельзя. Сейчас применение теории графов для решения классических ML-задач постепенно развивается, но пока медленно. В основном потому, что задач, где целесообразно переходить к графовому представлению, все равно мало. Сейчас на мировых конференциях угадывается тренд постепенного развития этой области, но в основном теории, а не практики. Библиотеки по работе с графами достаточно ограничены и плохо развиваются. Поиск аномалий — еще более редкая задача, поскольку осуществляется без разметки, и качество обнаружения аномалий можно оценить лишь экспертным путем. Во многих задачах переход к графовому описанию не целесообразен.
Если интересно почитать про стандартные методы обнаружения аномалий, то у я уже писал про это год назад на Хабре в этой статье.
Если вас интересует тема, то, чтобы получить больше информации, обязательно нужно идти в слак ODS (OpenDataScience), в каналы #network_analysis и #class_cs224w, смотреть курс Стэнфорда cs224w.
Еще недавно был прочитан курс по Knowledge Graphs. Ну и, конечно, нужно прочитать саму статью Graph based anomaly detection and description: a survey от авторов Leman Akoglu, Hanghang Tong, Danai Koutra (Akoglu, 2015), о которой идет речь в этом посте. Я перевел ее не всю, а только те фрагменты, которые счел важными, и понял в какой-то степени. Большинство авторов ссылаются именно на эту статью, потому что больше обзоров такого уровня и широты по теме нет. По крайней мере, я не нашел таких.
Список литературы
- Akoglu L, McGlohon M, Faloutsos C (2010) OddBall: spotting anomalies in weighted graphs. In: Proceedings of the 14th Pacific-Asia conference on knowledge discovery and data mining (PAKDD), Hyderabad, India, pp 410–421 https://link.springer.com/chapter/10.1007/978-3-642-13672-6_40
- Akoglu L, Faloutsos C (2010) Event detection in time series of mobile communication graphs. In: Proceedings of army science conference https://www.andrew.cmu.edu/user/lakoglu/pubs/EVENTDETECTION_AkogluFaloutsos.pdf
- Akoglu L, Vreeken J, Tong H, Duen HC, Tatti N, Faloutsos C (2013b) Mining connection pathways for marked nodes in large graphs. In: Proceedings of the 13th SIAM international conference on data mining (SDM), Texas-Austin, TX https://eda.mmci.uni-saarland.de/pubs/2013/dot2dot-akoglu,vreeken,tong,chau,tatti,faloutsos.pdf
- Akoglu, L., Tong, H. & Koutra, D. (2015) Graph based anomaly detection and description: a survey. Data Min Knowl Disc 29, 626–688. https://www.andrew.cmu.edu/user/lakoglu/pubs/14-dami-graphanomalysurvey.pdf
- Benczur AA, Csalogany K, Sarlos T, Uher M (2005) Spamrank: fully automatic link spam detection. In: Proceedings of the first international workshop on adversarial information retrieval on the web
- Box GEP, Jenkins G (1990) Time series analysis. Forecasting and Control, Holden-Day, Incorporated https://dl.acm.org/doi/book/10.5555/574978
- Bunke H, Dickinson PJ, Humm A, Irniger C, Kraetzl M (2006a) Computer network monitoring and abnormal event detection using graph matching and multidimensional scaling. In Proceedings of 6th industrial conference on data mining (ICDM), pp 576–590 https://dl.acm.org/doi/10.1007/11790853_45
- Castillo C, Donato D, Gionis A, Murdock V, Silvestri F (2007) Know your neighbors: web spam detection using the web topology. In: Proceedings of the 30th international conference on research and development in information retrieval (SIGIR), Amsterdam. ACM, pp 423–430 https://chato.cl/papers/cdgms_2006_know_your_neighbors.pdf
- Chakrabarti D (2004) Autopart: parameter-free graph partitioning and outlier detection. In: Proceedings of the 8th European conference on principles and practice of knowledge discovery in databases (PKDD), Pisa. Italy. Springer, New York, pp 112–124 https://dl.acm.org/doi/10.5555/1053072.1053085
- Chau DH, Akoglu L, Vreeken J, Tong H, Faloutsos C (2012) Tourviz: interactive visualization of connection pathways in large graphs. In: Proceedings of the 18th ACM international conference on knowledge discovery and data mining (SIGKDD), Beijing, China, pp 1516–1519 https://asu.pure.elsevier.com/en/publications/tourviz-interactive-visualization-of-connection-pathways-in-large
- Cortes C, Pregibon D, Volinsky C (2002) Communities of interest. Intell Data Anal 6(3):211–219 https://dl.acm.org/doi/10.5555/647967.741620
- Ding Q, Katenka N, Barford P, Kolaczyk ED, Crovella M (2012) Intrusion as (anti)social communication: characterization and detection. In: Proceedings of the 18th ACM international conference on knowledge discovery and data mining (SIGKDD), Beijing, China. ACM, pp 886–894 https://dl.acm.org/doi/10.1145/2339530.2339670
- Drineas P, Kannan R, Mahoney MW (2006) Fast monte carlo algorithms for matrices iii: computing a compressed approximate matrix decomposition. SIAM J Comput 36(1):184–206 https://epubs.siam.org/doi/abs/10.1137/S0097539704442702?mobileUi=0
- Eberle W, Holder LB (2007) Discovering structural anomalies in graph-based data. In: Proceedings of the international workshop on mining graphs and complex structures at the 7th IEEE international conference on data mining (ICDM), Omaha, NE. IEEE Computer Society, pp 393–398 http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.89.8477&rep=rep1&type=pdf
- Faloutsos C, McCurley KS, Tomkins A (2004) Fast discovery of connection subgraphs. In: Proceedings of the 10th ACM international conference on knowledge discovery and data mining (SIGKDD), Seattle, WA, pp 118–127 https://dl.acm.org/doi/10.1145/1014052.1014068
- Fayyad UM, Irani KB (1993) Multi-interval discretization of continuous-valued attributes for classification learning. In: Proceedings of the 5th international joint conference on artificial intelligence (IJCAI), Chambery, France. Morgan Kaufmann, pp 1022–1029 https://www.ijcai.org/Proceedings/93-2/Papers/022.pdf
- Gao H, Chen Y, Lee K, Palsetia D, Choudhary A (2012) Towards online spam filtering in social networks. In: Proceedings of the 19th annual network & distributed system security symposium http://cucis.ece.northwestern.edu/publications/pdf/GaoChe12.pdf
- Gyongyi Z, Garcia-Molina H, Pedersen J (2004) Combating web spam with trustrank. In: Proceedings of the 30th international conference on very large data bases (VLDB), Canada, Toronto, pp 576–587 https://www.vldb.org/conf/2004/RS15P3.PDF
- Kontkanen P, Myllymki P (2007) MDL histogram density estimation. J Mach Learn Res Proc Track 2:219–226 http://proceedings.mlr.press/v2/kontkanen07a/kontkanen07a.pdf
- Krishnan V, Raj R (2006) Web spam detection with anti-trust rank. In: Proceedings of the 2nd international workshop on adversarial IR on the Web at the 29th international conference on research and development in information retrieval (SIGIR), Seattle, WA, pp 37–40
- Lin J, Keogh E, Lonardi S, Chiu B (2003) A symbolic representation of time series, with implications for streaming algorithms. In: Proceedings of the ACM SIGMOD workshop on research issues in data mining and knowledge discovery (DMKD), San Diego, CA. ACM, pp 2–11 https://www.cs.ucr.edu/~eamonn/SAX.pdf
- Li Z, Xiong H, Liu Y, Zhou A (2010) Detecting blackhole and volcano patterns in directed networks. In: Proceedings of the 10th IEEE international conference on data mining (ICDM), Sydney, Australia. IEEE Computer Society, pp 294–303 http://datamining.rutgers.edu/publication/blackhole.pdf
- Molloy, Ian & Chari, Suresh & Finkler, Ulrich & Wiggerman, Mark & Jonker, Coen & Habeck, Ted & Park, Youngja & Jordens, Frank & Schaik, Ron. (2016). Graph Analytics for Real-time Scoring of Cross-channel Transactional Fraud.
- Muller E, Sanchez PI, Mulle Y, Bohm K (2013) Ranking outlier nodes in subspaces of attributed graphs. In: Proceedings of the 4th international workshop on graph data management: techniques and applications https://www.ipd.kit.edu/mitarbeiter/muellere/publications/GDM2013.pdf
- Rahman MS, Huang T.-K., Madhyastha HV, Faloutsos M (2012) Efficient and scalable socware detection in online social networks. In: Proceedings of the 21st USENIX conference on Security symposium (Security). USENIX Association, pp 32–32 https://dl.acm.org/doi/10.5555/2362793.2362825
- Rissanen J (1999) Hypothesis selection and testing by the MDL principle. Comput J 42:260–269 http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.22.9851&rep=rep1&type=pdf
- Rossi RA, Gallagher B, Neville J, Henderson K (2013) Modeling dynamic behavior in large evolving graphs. In: Proceeding of the 6th ACM international conference on Web search and data mining (WSDM), pp 667–676 https://www.cs.purdue.edu/homes/neville/papers/rossi-et-al-wsdm2013.pdf
- Sun J, Xie Y, Zhang H, Faloutsos C (2007b) Less is more: compact matrix decomposition for large sparse graphs. In: Proceedings of the 7th SIAM international conference on data mining (SDM), Minneapolis, MN http://www.cs.cmu.edu/~christos/PUBLICATIONS/sdm07-lsm.pdf
- Sun J, Xie Y, Zhang H, Faloutsos C (2008) Less is more: sparse graph mining with compact matrix decomposition. Stat Anal Data Min 1(1): 6–22. ISSN 1932–1864 https://onlinelibrary.wiley.com/doi/abs/10.1002/sam.102
- Tong H, Faloutsos C (2006) Center-piece subgraphs: problem definition and fast solutions. In: Proceedings of the 12th ACM international conference on knowledge discovery and data mining (SIGKDD), Philadelphia, PA, pp 404–413 http://www.cs.cmu.edu/~christos/PUBLICATIONS/kdd06CePS.pdf
- Tong H, Papadimitriou S, Jimeng S, Yu PS, Faloutsos C (2008) Colibri: fast mining of large static and dynamic graphs. In: Proceedings of the 14th ACM international conference on knowledge discovery and data mining (SIGKDD), Las Vegas, NV, pp 686–694 http://www.cs.cmu.edu/~htong/pdf/kdd08_tong_1.pdf
- Tong H, Lin C-Y (2011) Non-negative residual matrix factorization with application to graph anomaly detection. In: Proceedings of the 11th SIAM international conference on data mining (SDM), Mesa, AZ, pp 143–153 http://www.cs.cmu.edu/~htong/pdf/sdm11_tong.pdf
- Tong H, Lin C-Y (2012) Non-negative residual matrix factorization: problem definition, fast solutions, and applications. Stat Anal Data Min 5(1):3–15 https://asu.pure.elsevier.com/en/publications/non-negative-residual-matrix-factorization-problem-definition-fas
- Wang G, Xie S, Liu B, Yu PS (2011a) Review graph based online store review spammer detection. In: Proceedings of the 11th IEEE international conference on data mining (ICDM), Vancouver, Canada, pp 1242–1247 https://www.cs.uic.edu/~sxie/paper/ICDM-2011-final.pdf
Да, наша команда CleverDATA не только пишет и переводит статьи. Большую часть времени мы посвящаем решению интересных и разнообразных практических задач, для чего используем не только теорию графов, но и множество методов машинного и глубокого обучения.


anonymous
Картинка с графом повеселила ))