Экзибит, прокачай мой трансформер или Основные идеи по улучшению модели трансформера с 2018 по 2020 год (часть 1) / forpes.ru

Главная
Экзибит, прокачай мой трансформер или Основные идеи по улучшению модели трансформера с 2018 по 2020 год (часть 1)

Экзибит, прокачай мой трансформер или Основные идеи по улучшению модели трансформера с 2018 по 2020 год (часть 1) +18

23.08.2022 10:01

vladbalv 0 836 Источник

В июне 2021 года вышла статья “A Survey of Transformers” - обзор различных нововведений, сделанных с применением архитектуры “трансформер” после ее появления в материале “Attention is all you need”.

Этот материал особенно актуален сейчас. Приведенные подходы и архитектуры начинают использоваться сообществом с большим опозданием и понимание их работы становится востребованным постепенно, когда все уже понимают сильные и слабые стороны обычного трансформера и хотят его улучшить. Многие архитектуры, которые появляются сейчас, используют наработки, родившееся в первые три года после появления трансформеров.

Представляю в блоге ЛАНИТ обзор статьи “A Survey of Transformers”.

Про устройство трансфомеров написана уже не одна статья даже на Хабре, например, Transformer в картинках. Или можно посмотреть курсы Лены Войты или Валентина Малых.

В начале статьи “A Survey of Transformers” авторы напоминают об основных строительных блоках, на которых основывается архитектура. Я тоже тезисно их отражу в своем посте.

Описание стандартного (ванильного) трансформера

На вход архитектуре подаются последовательности векторов, чаще всего эмбеддингов некоторых категорий, например, частей слов. К каждому из этих векторов прибавляется вектор такого же размера, являющийся позиционным эмбеддингом, не зависящим от информации, закодированной в эмбеддингах, а лишь от порядкового номера каждого вектора в последовательности. В большинстве случаев эти векторы много раз проходят через различные преобразования, но все время остаются последовательностью векторов определенной длины.

Самым главным блоком в трансформерах является внутреннее внимание: каждый из векторов, который поступает на вход, преобразуется в три вектора тремя разными матрицами. Один из этих векторов называется query - это вектор, который учится “опрашивать” другие векторы на предмет наличия нужной ему информации. Другой - key - учится “понимать”, как дать понять другим векторам, что у него есть ценная для них информация, и value - та самая ценная информация, которой вектор хочет поделиться с другими.

На первом этапе query каждого вектора умножается на key каждого вектора, в результате чего получается матрица внимания размера lxl, где l - длина последовательности векторов. Далее в рамках каждого query мы имеем l его “связей” с key других векторов последовательности и нормируем их функцией softmax, чтобы вместе они суммировались в 1. Эти значения представляют собой веса, с которыми мы затем суммируем value для каждого query по отдельности. В матричном виде соответствующие операции можно выразить следующим образом:

$Attention(Q, K,V) = softmax(\frac{QK^T}{\sqrt{D_k}})V=AV$ $A= softmax(\frac{QK^T}{\sqrt{D_k}})$

Матрица A как раз и является матрицей lxl, выражающей то, как много информации возьмет один вектор от другого, чтобы пересмотреть свое значение на будущих слоях сети.

С концепцией внутреннего внимания непосредственно связана концепция многоголового multihead-внимания. Заключается она в параллельном наличии некоторого количества слоев внутреннего внимания, которые затем стыкуются в длинные векторы и преобразуются через умножение на еще одну матрицу к изначальному размеру.

$where head_i=Attention(QW_i{^Q},KW_i{^K},VW_i{^V}).$

Еще одна концепция - это position-wise feed forward network, еще одно умножение на матрицу или же применение полносвязного или линейного слоя к данным, а точнее двух слоев с функцией активации в промежутке. При этом это преобразование с одной и той же матрицей применяется к каждому вектору по отдельности.

Наконец, в архитектуре трансформера есть residual-связи, т.е. связи в обход некоторых слоев, а именно многоголового внимания и position-wise полносвязной сети. После этого проброса и сложения с теми векторами, которые через эти слои пошли, производится Layer-нормализация - из каждого вектора вычитается его среднее и делится на стандартное отклонение, после чего еще умножается на некоторый коэффициент и прибавляется еще некоторое поправочное число.

Основной недостаток сети трансформер связан с наличием квадратичной зависимости от длины последовательности как для вычислений, так и для оперативной памяти, и большая часть исследований так или иначе была нацелена на преодоление этой проблемы и касалось механизма многоголового внимания. В первой части будем обсуждать только модификации этого элемента архитектуры.

Ограниченное внимание и его сочетания

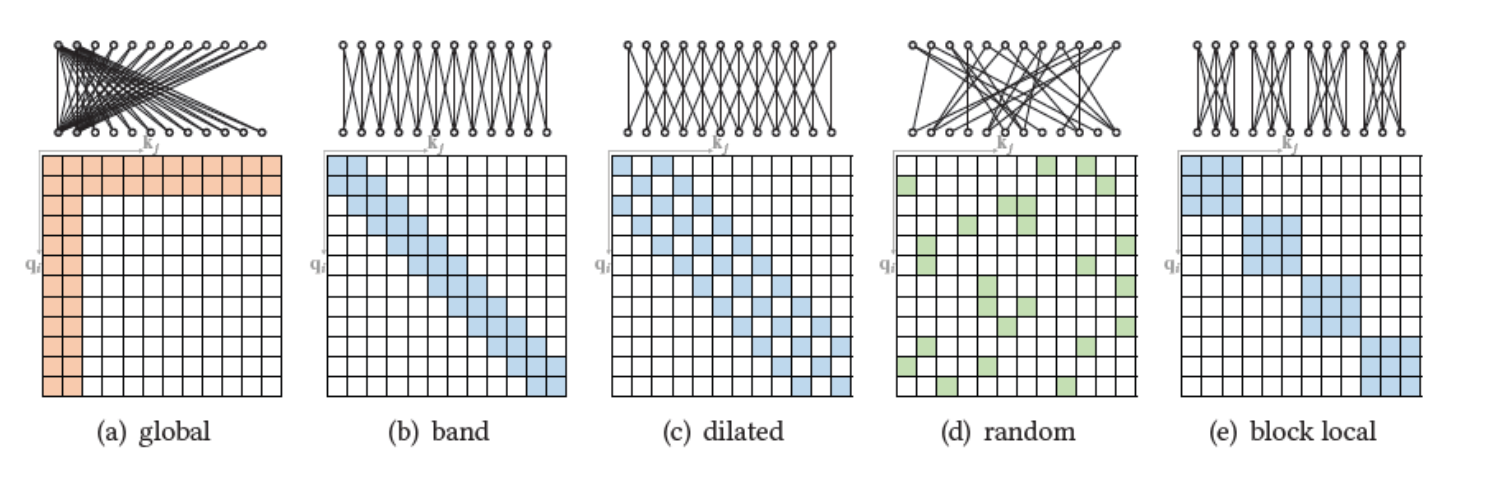
Самое простое решение именуется “разреженным внутренним вниманием” и заключается в ограничении связей векторов друг с другом для расчета матрицы внимания. Для удобства восприятия эти ограничения иногда рассматриваются в виде графов. Авторы приводят наиболее принятые возможности.

Global - все векторы связываются лишь с несколькими ведущими векторами, которые берут информацию у всех остальных векторов для того, чтобы обновить свои значения и дают информацию всем остальным векторам. Остальные же векторы друг с другом никакой информацией не делятся.
Band или local - векторы связываются друг с другом лишь в некотором окне (например, два вектора назад и два вектора вперед).
Dilated - векторы связываются друг с другом в некотором окне, но с промежутками (например, только два, четыре и шесть векторов влево и вправо).
Random - связи между векторами устанавливаются случайным образом.
Block local - связи между векторами ограничиваются блоками. Так, например, первые пять векторов связаны только друг с другом, вторые пять векторов (с пятого по десятый) связаны только друг с другом и т. д.

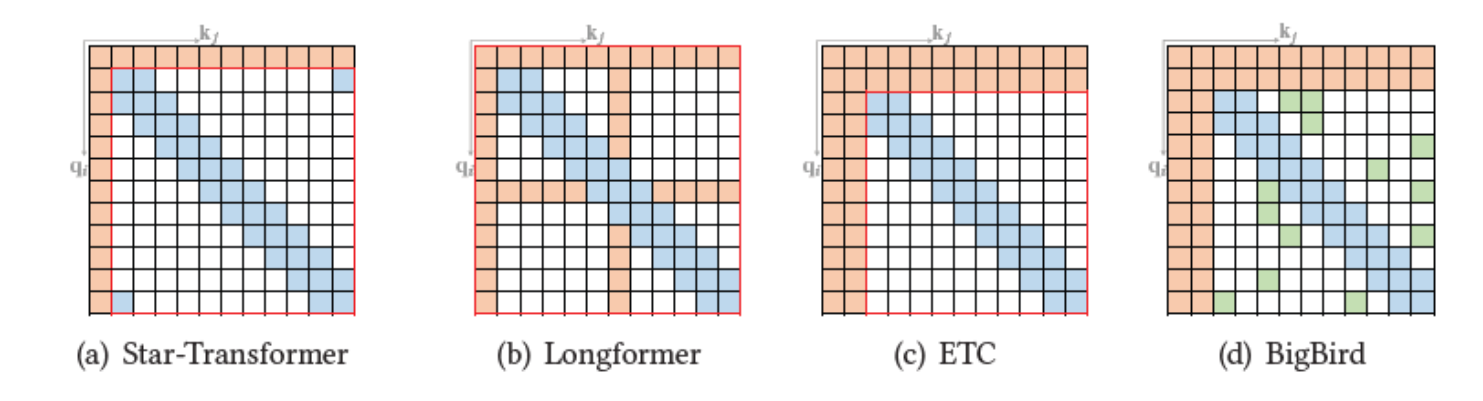
На практике же конкурентные архитектуры содержат, как правило, некоторое сочетание из этих подходов.

Например, Star-Transformer (https://aclanthology.org/N19-1133/) и Longformer (https://arxiv.org/abs/2004.05150) и ETC (https://aclanthology.org/2020.emnlp-main.19/) содержат global и local внутреннее внимание.
BigBird (https://arxiv.org/abs/2007.14062) содержит global, local и random.

Сочетания различных видов разреженного внимания в архитектурах трансформеров

Такой подход позволяет сократить число расчетов и хранимых в памяти значений матрицы внимания и с меньшими расходами увеличить длину последовательности поступающей на вход сети.

Отдельный вид разреженного внимания в статье именуется extended, т.е. расширенный. Это внимание через бинарное дерево и через двумерные координаты.

Внимание через бинарное дерево (в BP-Transformer: https://arxiv.org/abs/1911.04070) проиллюстрировано следующим образом:

Внимание через бинарное дерево (Binary partitioning (BP) Transformer(T))

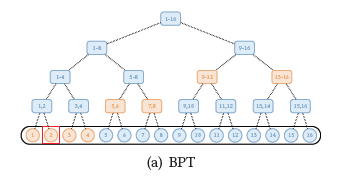
Таким образом, формируется много дополнительных узлов, которые авторы называют span nodes. Они как бы экранируют свои дочерние узлы, принимая все внимание на себя. Чем дальше токены расположены друг от друга в последовательности, тем более высоким по иерархии узлам они будут давать о себе информацию, а общаться каждый с каждым не будет.

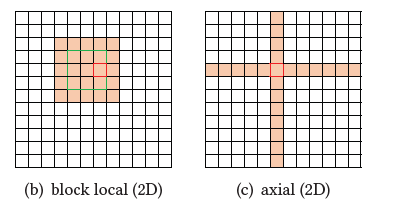
У трансформеров для работы с изображениями свои хаки (http://proceedings.mlr.press/v80/parmar18a.html). В статье описываются два подхода по формированию связей внимания: block local и axial. В обоих случаях формирование связей идет до преобразования картинки из двумерной в одномерную. Первый подход позволяет учитывать связи внутри квадрата, а второй - по горизонтальным и вертикальным направляющим каждого пикселя.

Разреженное внимание, основанное на двумерной структуре данных

Разреженное внимание основанное на содержании (Content-based Sparse attention)

Основная цель подхода - найти наиболее ближайшие ключи (key) к запросам (query), не вычисляя всех попарных скалярных произведений, как мы делаем в ванильном внимании. Для решения этой задачи есть свои подходы под общим названием Maximum Inner Product Search (https://en.wikipedia.org/wiki/Maximum_inner-product_search). Но можно и проще: в Rounting Transformer (https://arxiv.org/abs/2003.05997) используется K-means для key и query в одном пространстве. Соответственно, когда у нас появляются новые ключи, мы для каждого запроса смотрим, в какой кластер он попал и считаем веса внимания лишь с теми ключами, которые принадлежат этому же кластеру. В Reformer подход похожий, только вместо K-means используется Locality Sensitivity Hashing (https://ru.wikipedia.org/wiki/Locality-sensitive_hashing), та же кластеризация в некотором роде: для близких query и key будут одинаковые хэши.

Еще две концепции в этом разделе - это Sparse Adaptive Connection (https://proceedings.neurips.cc/paper/2020/hash/c5c1bda1194f9423d744e0ef67df94ee-Abstract.html) и Sparse Sinkhorn Attention (http://proceedings.mlr.press/v119/tay20a.html). Первый подход использует LSTM-нейросеть для предсказания пар токенов, между которым должна быть связь, которая обучается с подкреплением. Второй разбивает все ключи и запросы на отдельные подмножества, блоки. Затем с помощью Sinkhorn-нормализации подбирает такую матрицу связей между блоками ключей и запросов, чтобы каждый блок ключей был связан только с одним блоком запросов, что осуществляется через отдельную нейросеть Sortnet.

Линеаризованное внимание

Наконец, в статье рассматривается “Линеаризованное внутреннее внимание” (Linearized sef-attention). Основная мысль этой концепции в том, что умножение

ведет к квадратичной сложности, а вот если бы мы не брали от произведения нелинейную функцию Softmax, то могли бы сначала умножить

а потом уже на Q, и жизнь стала бы проще. Как этого добиться? Попробовать сделать что-то с Q и K по-отдельности, превратив их в Q’ и K’, чтобы их произведение давало тот же результат, как и после софтмакса над произведением Q и K. Это произведение можно кроме того переосмыслить, представив

как функцию близости векторов

которую можно уже представить в виде произведения двух функций

$\phi(q_i) ; \phi(k_j).$

Если мы такую функцию подобрали, то вполне можем сначала посчитать произведение

$\phi(k_j)$

на v, а потом уже умножать на

$\phi(q_i).$

При этом выделенные синим фрагменты в случае авторегрессионного внутреннего внимания (то, с которым мы сталкиваемся в декодере, когда новый токен может взаимодействовать посредством внимания лишь с предыдущими токенами, но не со следующими) могут не пересчитывать заново полностью, а лишь дополняться новыми членами.

В качестве функций предлагаются elu(x)+1 в Linear-трансформере (http://proceedings.mlr.press/v119/katharopoulos20a.html). А авторы Performer (https://arxiv.org/abs/2009.14794) стараются обобщить задачу, представляя функцию следующим образом:

$\phi(x)= \frac{h(x)}{\sqrt m}[f_1(\omega_1^Tx),...,f_1(\omega_m^Tx),...,f_l(\omega_1^Tx),...,f_l(\omega_m^Tx)]$

Здесь функция

Результат применения функции f конкатенируется в единый вектор. В качестве варианта этих функций предлагается:

$h(x)= exp(\frac{\|x\|^2}{2}), l=2,f_1=sin, f_2=cos$

$h(x)=exp(-\frac{\|x\|^2}{2}), l=1, f_1=exp$

Некоторые авторы также пытаются улучшить механизм работы с авторегрессионным самовниванием. В изначальной парадигме новые члены

просто постепенно добавляются к общей сумме. В Random Feature Attention (https://openreview.net/forum?id=QtTKTdVrFBB) авторы предлагают некоторый механизм гейтинга, для того чтобы выбрать лишь определенные связи (в основном локальные). Осуществляется это посредством весов g у нового члена и (1-g) у предыдущей суммы, которые являются функцией входных данных.

Прототипирование запросов и сжатие памяти

Авторы приводят еще два механизма сокращения расчетов матрицы внимания. Первый нацелен на уменьшение числа запросов, второй - на уменьшение числа пар “ключ-значение”.

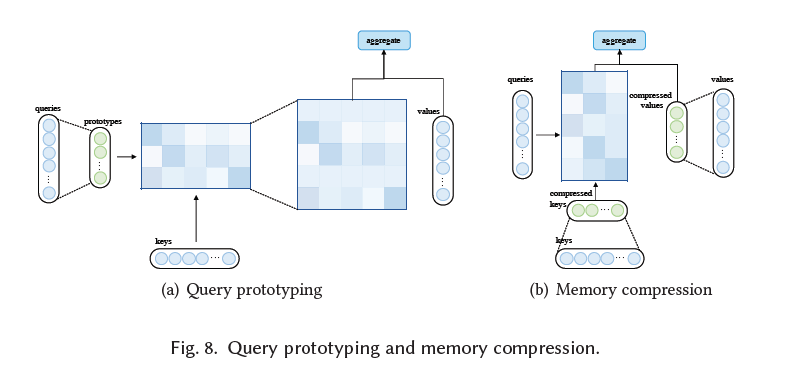
Для того, чтобы уменьшить число запросов, предлагается самый простой подход, по которому сначала выбираются каким-то образом прототипы из запросов (query), матрица внимания рассчитывается на их основе, а остальные строки матрицы заполняются равномерным распределением. Есть и более интересные подходы, например, в Clustered Attention (https://arxiv.org/abs/2007.04825) запросы кластеризуются и веса внимания вычисляются для центроидов кластеров, а затем просто ставятся в соответствие для всех запросов, принадлежащих кластеру.

В Informer измеряют некоторую меру разреженности запросов через дивергенцию Кульбака-Лейблера между распределением внимания векторов внимания запросов и равномерным распределением. По этой мере выбираются top-u запросов, а оставшиеся веса внимания берут из равномерного распределения. Понятно, чтобы все это сделать, нужно уже иметь посчитанными все веса внимания, и не ясно, какой в этих процедурах тогда смысл. На самом деле авторы придумали некоторый хак, как это обойти. Подробнее о нем вы можете почитать самостоятельно в статье.

Memory Compressed Attention (https://openreview.net/forum?id=Hyg0vbWC-), напротив, призван уменьшить число ключей и значений через шагающую (strided) свертку. Другой подход для сжатия памяти ключ-значение применяется в Set Transformer (http://proceedings.mlr.press/v97/lee19d.html). Авторы статьи, которую я здесь обозреваю, пишут, что в нем и в архитектуре Luna (https://arxiv.org/abs/2106.01540) используются глобальные узлы, но только для того, чтобы получить пары “ключ-значение”, а вот запросы берутся все. В самой же статье по Set Transformer приводится достаточно сложная концепция induced set attention блока.

Архитектурные изменения при замене стандартного многоголового внимания на блок set attention (SAB) и induced set attention (ISAB)

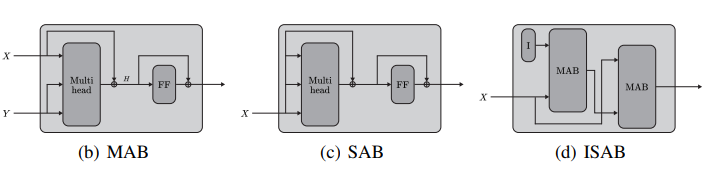
К нему они приходят через просто set attention block, в котором Q=K=V=X. В случае же ISAB берутся некоторые глобальные обучаемые вектора I в качестве запросов. Затем выход этого многоголового внимания подается как ключи и значения в другое многоголовое внимание, а то, что первому блоку служило как ключ и значение (равные), теперь является запросом для второго блока.

После того, как мы узнали про концепцию с шагающими свертками, могут возникнуть всякие схожие идеи, и действительно еще один подход используется авторами Linformer (https://arxiv.org/abs/2006.04768): линейный слой используется для проецирования ключей и значений. Важно отметить, что слой мог бы применяться, чтобы уменьшить размерность каждого вектора (d -> d’), но здесь его используют именно по другой размерности, чтобы из l длина последовательности) ключей и значений сделать l’. Наконец, Poolingformer (https://arxiv.org/abs/2105.04371) используют два уже описанных похода: внимание в скользящем окне и затем уже сжатие пар “ключ-значение”, которое они осуществляют операциями пулинга.

Низкоранговое внутреннее внимание

Многие авторы пишут, что матрица внимания низкого ранга, т.е. ее ранг значительно меньше числа токенов l. Особенно это должно быть применимо для коротких последовательностей с большим числом PAD токенов. Соответственно, использование ее в полном виде может быть неэффективным. Чтобы решить эту проблему, авторы одной из статей раскладывают матрицу внутреннего внимания в низкоранговую для учета дальних взаимодействий и на матрицу с внутренним вниманием со скользящим окном.

В других работах предлагается использовать низкоранговую апроксимацию. Одна из линий работ в этом направлении - использование метода Нистрома (Nystrom (https://en.wikipedia.org/wiki/Nyström_method). В рамках этого подхода сначала выбираются узлы-прототипы (например, через шагающий усредняющий пулинг). В таком случае матрицу А можно аппроксимировать следующим образом:

$\overline{A}=softmax({Q}{\overline{K}}^T)(softmax({\overline{QK}^T)}^{-1} softmax(\overline{Q}K^T),$

где

$\overline{Q};\overline{K}$

это запросы (ключи), полученные только для прототипов.

Важно отметить, что матрица

$M^{-1}=(softmax\overline{QK}^{T})^{-1}$

не всегда существует, поэтому авторы CSALR добавляют к ней единичную. В Nystromformer (https://arxiv.org/abs/2102.03902) авторы используют псевдообратную матрицу M вместо обратной, что важно в том случае, если M окажется вырожденной.

Априорное распределение внимания

Хотя механизм внимания нацелен на самостоятельную установку необходимых “связей” между токенами, иногда есть смысл “подсказывать” этому механизму, складывая или умножая матрицу внимания на какую-то заранее определенную.

Сочетание обычного внутреннего внимания и априорного

И первая описываемая авторами концепция схожа с разреженным вниманием в скользящем окне, но вместо фиксированного окна взвешивает все веса ядром Гаусса. Таким образом получается, что мы вводим априорное распределение Gij, и чем выше эта вероятность, тем больше связаны узлы i и j. Yang et al. (https://aclanthology.org/D18-1475/) предлагают использовать

$G_{ij}=-\frac{(j-p_i)^2}{2\sigma^2},$

где

это индекс центральной позиции (ключа) для каждого запроса

который определяется отдельной полносвязной нейросетью. В Gaussian Transformer (https://ojs.aaai.org//index.php/AAAI/article/view/4614) наилучшей позицией ключа для

считается i (диагональ), а

$G_{ij}=-\mid{w}(i-j)^2+b \mid,$

где w>=0, b<=0 являются скалярами, контролирующими отклонение и уменьшение веса центральной позиции соответственно.

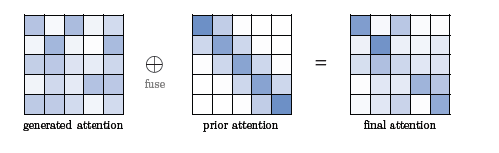
Другой подход предлагает модулировать матрицу внимания более высоких слоев трансформера матрицами более низких. Например, так:

$\widehat{A}^{(l)}=w_1\ast{A}^{(l)}+w_2\ast{g}(A^{(l-1)}),$

l здесь - это номер слоя, а

веса, g - некоторая функция. В Predictive Attention Transformer (https://openreview.net/forum?id=YQVjbJPnPc9) в качестве g используется сверточный слой, а

а в Realformer (https://arxiv.org/abs/2012.11747) g отсутствует (или можно представить ее как тождественное отображение), а

Авторы говорящего названия Lazyformer (https://arxiv.org/abs/2102.12702) просто предлагают шарить матрицу А между ближайшими слоями (переключаясь между

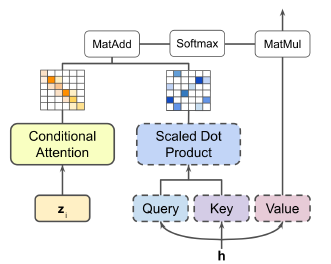
Также в обзорной статье описывается отдельный подход с мультизадачными адаптерами (https://openreview.net/forum?id=de11dbHzAMF) предлагая фреймворк CAMTL (Conditionally Adaptive Multi-Task Learning). В таком подходе матрица внимания модулируется некоторой матрицей M, которая при этом является функцией задачи или некоторого эмбеддинга задачи zi.

Формулируется это следующим образом:

Матрица делится на m квадратов, поэтому

$A_j\in{R}^{(n/m)\ast(n/m)}$

и являются обучаемыми параметрами, а не реальной матрицей внимания, а и являются функциями, преобразующими эмбеддинг задачи в пространство

$R^{(n/m)\ast(n/m)}.$

Затем получившаяся матрица A’ складывается с реальной матрицей А.

Использование мультизадачных адаптеров для модулирования матрицы внимания

После Lazyformer неудивительно, что некоторые группы пошли дальше и решили проверить, а можно ли сделать трансформер, где внутреннее внимание просто захардкожено, т.е. не зависит от текущего входа. Так, например, Zhang et al. (https://aclanthology.org/P18-1166/) вместо формирования весов внимания просто кумулятивно складывают эмбеддинги токенов. Тем не менее, делают не только это, а затем используют отдельный полносвязный слой для того, чтобы посчитать веса, через которые складывать эмбеддинг текущего токена и кумулятивное среднее. You et al. (https://doi.org/10.18653/v1/2020.acl-main.687) предлагают использовать нормальное распределение вместо матрицы внимания, а в Synthesizer (https://arxiv.org/abs/2005.00743) авторы придумали выучивать матрицу А, а не определять из токенов. Промежуточный вариант, который они назвали Synthesizer (Dense), производил матрицу A непосредственно из эмбеддингов токенов через полносвязный слой (т.е. переводили векторы длиной d в вектора длиной l). Получается, что каждый токен, обладая лишь информацией о себе, пытается догадаться о том, какая информация ему нужна от других токенов, о которых он ничего не знает.

Улучшаем многоголовое внимание

В первую очередь авторы обзора указывают на проблему: в ванильном трансформере нет никаких ограничений на различия между матрицами внимания разных голов. Соответственно, ничто не мешает им сделаться одинаковыми. Например, частая ситуация бывает, что основное внимание фокусируется на специальных токенах. Различные работы пытаются эту проблему решить. В целом есть два пути для этого: или мы вводим взаимодействие между головами, подталкивая их выучиться по-разному самостоятельно, или же вводим некоторые ограничения на функцию ошибки.

Так Li et al. (https://aclanthology.org/D18-1317/) вводят регуляризирующие добавки к функции ошибки:

$D_{subspace}=-\frac{1}{H^2}\displaystyle\sum_{i=1}^{H}\displaystyle\sum_{j=1}^{H}{\frac{{v^i}\ast{v^j}}{{\|v^i\|}{\|v^j\|}}}$ $D_{position}=-\frac{1}{H^2}\sum_{i=1}^{H}\sum_{j=1}^{H}V|A^i \odot{A^j}|$ $D_{output}=-\frac{1}{H^2}\displaystyle\sum_{i=1}^{H}\displaystyle\sum_{j=1}^{H}{\frac{{o^i}\ast{o^j}}{{\|o^i\|}{\|o^j\|}}}$

Эти добавки ограничивают попарные скалярные произведения значений

$(D_{subspace}),$

ограничивают поэлементное перемножение матриц внимания

$(D_{position})$

и попарные скалярные произведения выходов внимания

$(D_{output})$

разных голов (i, j индексы разных голов).

Другой подход заключается в добавлении лосса, который подгоняет матрицу А под определенный паттерн (например, такой, как у внутреннего внимания в скользящем окне или как у глобального внутреннего внимания). Sukhbaatar et al. (https://aclanthology.org/P19-1032/) предлагают использовать выучиваемую длину окна, параметризуемую выучиваемым числом z и гиперпараметром R:

Таким образом, каждая голова подталкивается к выучиванию своего собственного окна внимания.

Авторы Multi-Scale Transformer (https://ojs.aaai.org//index.php/AAAI/article/view/6290) также предлагают использовать разные размеры окна для разных голов и слоев, при этом основывая это на языковом базисе и на эмпирических исследованиях, по которым у более высоких слоев BERT получаются большие размеры окон, чем у более низких (общий текстовой контекст в сравнении с локальным).

Авторы далее переосмысляют последнее преобразование в рамках многоголового внимания: линейный слой поверх конкатенированных выходов отдельных голов для того, чтобы восстановить изначальную длину последовательности. Это эквивалентно перемножению матрицы WV и WO для каждой головы отдельно, а потом сложение выходов от таких голов. Такой подход видится достаточно слабым, и поэтому некоторые авторы стараются его улучшить. Один из подходов вдохновлен капсульными нейронными сетями и использует роутинг для агрегации информации от разных голов. Две приведенные авторами работы используют динамический роутинг и EM-роутинг. Обратной стороной является увеличение вычислительных затрат на такие вычисления, поэтому Li et al. (https://aclanthology.org/N19-1359/) эмпирически показывают, что такой подход достаточно применить лишь на нижних слоях.

Авторы обзора приводят еще одну интересную концепцию: шаринг пар “ключ-значение” между головами, т.е. только запросы для разных голов будут различаться.

***

На этом первая часть нашего обзора заканчивается. Мы привели почти все подходы, описанные в оригинальной статье, которые нацелены на улучшения многоголового внутреннего внимания, ключевого элемента трансформеров и наиболее затратного с точки зрения вычислений. По приведенным работам видно, что уже есть масса способов бороться со всем известной квадратичной зависимостью от длины последовательности, по модулированию внутреннего внимания определенными распределениями и по улучшению многоголового внимания для достижения большей емкости модели при обучении. Во второй части опишем модификации других модулей трансформера и различные идеи по преобразованию их архитектуры в общем.

Кого особенно заинтересовал материал, во-первых, конечно, рекомендую посмотреть оригинальную статью, а еще и обратить внимание на youtube-канал (https://www.youtube.com/c/YannicKilcher), автор которого делает разборы большинства популярных статей, и на курс от Стэнфорда по трансформерам.