Компания IBM опубликовала на GitHub исходный код набора инструментов FHE для Linux. Утилиты работают на платформах IBM Z и x86, поддерживаются Ubuntu, Fedora и CentOS.
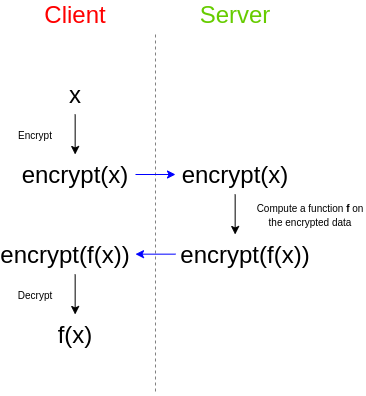
Полностью гомоморфное шифрование (FHE) долгое время считалось чем-то вроде чаши святого Грааля в криптографии. Задача действительно казалась нереальной. Тип шифрования FHE предполагает манипуляции зашифрованными данными третьей стороной без возможности расшифровки самих данных или результата манипуляций.
Как такое возможно?
В качестве простого примера представьте, что у вас есть набор электронных писем, и вы хотите использовать сторонний спам-фильтр, чтобы проверить, являются ли они спамом. Спам-фильтр работает на сервере, потому что разработчик старается сохранить конфиденциальность своего алгоритма: либо скрывает исходный код, либо спам-фильтр зависит от очень большой базы данных, которую они не хотят раскрывать публично, так как это облегчает атаку, либо и то, и другое. Неважно, главное, что спам-фильтр в любом случае работает на сервере — и вы никак не можете запустить его у себя. Что делать в такой ситуации? Вы тоже заботитесь о конфиденциальности своих данных и не хотите передавать третьим лицам содержание электронных писем в открытом, незашифрованном виде. Здесь на выручку приходит полностью гомоморфное шифрование:
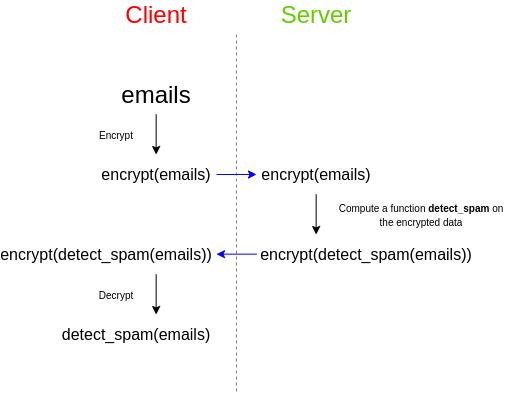
Таким образом, сервис хранит в секрете алгоритм, а вы храните в секрете свои данные. Но FHE позволяет успешно применять алгоритм на этих данных, так что ни одна сторона на узнаёт секреты другой.
Полностью гомоморфное шифрование имеет множество применений, в том числе и в блокчейне, где сервер может манипулировать зашифрованными данными клиента без раскрытия содержимого информации. То есть сервер может выполнять запросы клиента, не зная, что он запросил.
Другие варианты применения гомоморфного шифрования:
- Более эффективные протоколы скрытых адресов и более общие решения масштабируемости для протоколов сохранения конфиденциальности, которые сегодня требуют от каждого пользователя лично сканировал весь блокчейн на предмет входящих транзакций.
- Обмен данными с сохранением конфиденциальности, которые позволяют пользователям выполнять некоторые конкретные облачные вычисления над своими данными, сохраняя при этом полный и единоличный контроль над ними.
- Как компонент более мощных криптографических примитивов, таких как более эффективные протоколы конфиденциальных вычислений (двусторонняя версия иллюстрируется классической задачей миллионеров, в которой два миллионера хотят выяснить, кто из них богаче, не разглашая точную сумму своего благосостояния).
Вообще, существуют различные виды гомоморфного шифрования, некоторые более мощные, чем другие. Они отличаются тем, какие операции можно произвести с зашифрованными данными.
Частично гомоморфное шифрование позволяет произвести только одну операцию с зашифрованными данными: либо сложение, либо умножение
Отчасти гомоморфное шифрование (somewhat homomorphic) полноценно работает только на ограниченном наборе данных.
Наконец, полностью гомоморфное шифрование позволяет неограниченные операции сложения и умножения на любом массиве данных.
Реализовать частичное гомоморфное шифрование довольно легко: например, умножение реализовано в RSA:
, , так что
Эллиптические кривые предлагают аналогичный вариант со сложением. А вот реализовать одновременно и сложение, и умножение гораздо сложнее. Поиски такой схемы продолжались с 1978 года, когда Ривест, Адлеман и Дертузос сформулировали задачу и ввели термин «гомоморфное шифрование». В течение 30 лет существование полностью гомоморфных систем не было доказано, а сам Ривест решил, что идея не подлежит реализации.
Серьёзный прорыв произошёл только в 2009 году после публикации кандидатской диссертации стэнфордского аспиранта Крейга Джентри. Он описал возможную конструкцию полностью гомоморфной криптосистемы на идеальных решётках. В диссертации он также предложил инновационную идею бутстраппинга. Этот трюк превращает схему частичного FHE в схему полностью гомоморфного шифрования. Метод бутстраппинга изображён на диаграмме ниже. Если вкратце, то здесь биты секретного ключа шифруются публичным ключом в гомоморфной схеме и публикуются как «бустрапперский ключ», что позволяет исполнить гомоморфное шифрование на перешифрованном шифротексте, в котором шум уменьшается до размеров исходного. То есть мы «освежаем» шифротекст, как бы стирая ошибку старого ключа.
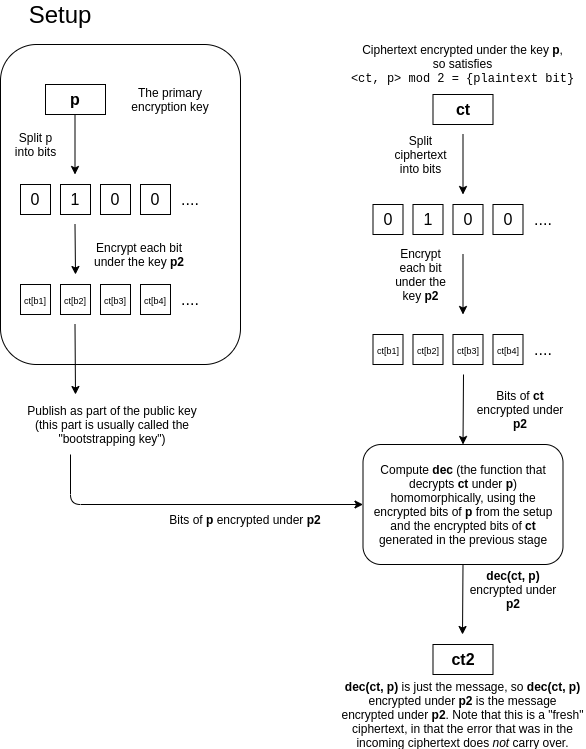
Проще выражаясь, процедура расшифровки сама по себе является вычислением, поэтому может быть реализована как гомоморфная схема, которая принимает на входе биты шифротекста и биты секретного ключа.
Криптографическая схема Джентри стала серьёзным прорывом, но вводила новую ошибку, которая не зависит от количества ошибки в исходном шифровании. Сам автор описал сложное решение проблемы, но более удачной стала доработанная схема Бракерски и Вайкунтанатана, предложенная в 2011 году (схема получила название BGV (Бракерски-Гентри-Вайкунтанатан). В 2013 году IBM выпустила свободную криптографическую библиотеку HELib с поддержкой гомоморфного шифрования и схемы BGV. В январе 2020 года вышла версия HELib 1.0.0.
В 2013 году Джентри снова заявил о себе. С соавторами Сахаи и Уотерсом и представил схему полного гомоморфного шифрования третьего поколения — схему GSW (Gentry, Sahai, Waters), которая опять использует криптографию на решётках и бустраппинг.
За годы разработки на базе HELib создан полноценный набор инструментов с интегрированными образцами для IDE, которые работают сразу «из коробки».
Ранее IBM уже выпустила инструменты полностью гомоморфного шифрования для MacOS и iOS. В перспективе обещает опубликовать исходный код версии для Android.
Версия для Linux выпущена скорее в демонстрационных целях и работает на базе данных с европейскими странами и их столицами (второй пример для финансовой отрасли представляет собой распознавание фрода нейросетью на зашифрованной базе анонимных транзакций). До практического применения гомоморфного шифрования пока дело не дошло. По оценке самого Джентри в 2009 году, например, обработка поискового запроса в Google в случае, если текст зашифрован, потребует примерно в триллион раз больше вычислений. Тем не менее, сделанные IBM оптимизации позволили существенно повысить производительность библиотеки, так что через несколько лет или десятилетий, она вполне может найти широкое применение в веб-приложениях. IBM заявляет, что уже сейчас библиотеку можно запускать на мейнфреймах IBM Z.


osmanpasha
Гм. Кто-то может объяснить, как можно определить, является ли письмо спамом, не зная, что в письме? Или в статье пример некорректный?
Daddy_Cool
Присоединяюсь к вопросу.
«обработка поискового запроса в Google в случае, если текст зашифрован, потребует примерно в триллион раз больше вычислений».
Т.е. сам Гугл не будет знать, что я там ищу? Но вряд ли это надо Гуглу.
AWSVladimir
Вот полностью согласен.
Пришло письмо «Продам булочки»
Клиент зашифровал сообщение в «As%6vD7;!» и отправил на сервер и?..
Тут либо сервер умеет расшифровывать сообщение и детектить по базе, либо кто то что то не договаривает.
Конечно с письмом можно:
Head — не шифруем
Body — шифруем
Тогда сервер проверяет только адреса и заголовок, сверяясь с базой, не проверяя тело письма, но это совсем не то, о чем написано в статье.
И как можно:
Это вообще как?
Отправляя как выше в примере запрос «As%6vD7;!» по поиску клиентов кому нужны булочки, как сервер может дать клиентскую базу покупателей булочек, не расшифровав сам запрос?
Автор, велком с объяснениями!
Если булочки зашифрованы на сервере как «6vD7;!» а покупатели как «As%», то сервер может что то искать, но это совсем не то, это поиск по словарю, тогда вместо слов можно использовать только цифры. Но это не шифрование.
Объясните плиз с примером:
Клиент: «Продам булочки» -> «As%6vD7;!» (шифро сообщение на сервере)
PS: И тут пример только со статическим шифрованием, когда в любое время зашифрованное сообщение будет всегда идентичным, а если оно каждый раз будет разным, то это еще интереснее и непонятнее как это технически возможно.
Как не зная что в сообщении можно выполнить это сообщение?
— Fullmoon
Отвечу тут, тк ограничен в высказываниях.
Как вы вычислите если у 100 клиентов разный ключ щифрования, при этом допустим что один алгоритм шифрования.
Как вы без ключа узнаете содержимое?
У 100 человек будет 100 различных шифро-текстов «Продам булочки», а не одно на все 100 человек, иначе это не шифрование, а глупость какая то.
Undiabler
Все правильно. Идея такого шифрования в следующем фокусе:
1. Клиент №1 шифрует сообщение и отправляет на сервер:
crypt("Продам булочки") -> «g2fa1 h4hxc»
2. Сервер получает сообщение и вычисляет md5 хеш (например) от каждого слова не расшифровывая исходники:
g_md5(«g2fa1 h4hxc») -> "66096db4d3126b086f289e17386e2773 0e5b3c4b2b8314e67104e486ea202524"
3. Хеш от слова «Продам» к примеру находится в спам листе и сервер маркирует письмо как спамовое.
4. Клиент №2 отправляет письмо «Продам гараж». Письмо попадает в спам потому что сервер вычислил хеши и нашел слово «Продам» не раскрывая самого слова (только его хеш).
Вся соль фокуса заключается том что мы можем получить вычисления над данными не расшифровывая их. Для того чтоб шифрование было вправду гомоморфным следующие преобразование должны быть истинными:
crypt("Продам булочки") -> g_md5("g2fa1 h4hxc") -> "66096db4d3126b086f289e17386e2773 0e5b3c4b2b8314e67104e486ea202524"
crypt("Продам гараж") -> g_md5("h4j64 j5gnb") -> "66096db4d3126b086f289e17386e2773 ac9ad57eab568489aa8cd9f69f5c461c"
merhalak
Слишком упростил, поскольку, в таком случае, можно будет составлять таблицы хешей и частотным методом расшифровать письмо, либо получив наиболее близкий вариант.
Undiabler
Вы правы, хеширование в контекста гомоморфного шифрования это вообще отдельная тема.
Я постарался обьяснить на пальцах как это может выглядеть на предложенном примере с спам-фильтром.
Именно такой подход с частичными хешами сейчас реализован в спам-фильтре razor2 (без гомоморфного шифрования).
barbalion
Не упростил, а исказил.
Суть этого гомоморфного шифрования в том, что спам-фильтр, произведя вычисления над зашифрованными данными, сам не будет знать результата (является ли письмо спамом или нет). Узнает об этом только владелец информации, расшифровав своим ключом ответ от фильтра.
Это работает так: допустим все вычисления байесовской вероятности того, что письмо — спам, происходят над зашифрованными данными с помощью только 2 операций: сложения и умножения. В итоге получается какое-то зашифрованное нечто, которое фильтр сам интерпретировать не сможет. Итоговую оценку вероятности узнает только владелец информации, расшифровав ответ. Но он не сможет понять, как эта оценка была получена (сам алгоритм) из исходной посылки, потому что у него только конечный результат.
Как реализовать байесовский (хотя бы) фильтр (с разбиением текста на отдельные токены и пр.) с помощью только сложения и умножения — это, я думаю, будет предметом еще чьей-нибудь докторской диссертации. Что-то мне подсказывает, что работать оно будет оооочень неторопливо. Это же как кораблик внутри бутылки пинцетом собирать.
Playa
Почему-то вспомнился movfuscator
mikhanoid
Алгоритмы можно свести к арифметике над натуральными числами (кодировка Гёделя), но работать это будет очень неспешно. Сложно представить практическую пользу такого неспешного метода. Странно, что все примеры в статье довольно абстрактные. Хотя бы показали, как это может работать для блокчейнов.
Tarakanator
Спасибо, к сожалению поставить плюс не могу, поэтому благодарю так.
osmanpasha
Это выглядит, как довольно паршивый алгоритм шифрования, т.к. достаточно прогать через него все слова из словаря, чтобы научиться по хэшу декодировать слово. Потом владелец сервера может смотреть логи и понять, что все запросы, на которые сервер вычисляет 66096db4d3126b086f289e17386e2773, содержат слово "Продам". Я понимаю, что это только пример, но в самой статье такие же плохие примеры(
gchebanov
Не, все интереснее.
Для того что бы сервер не мог узнать запрос, ему нужно будет его "смешать" со всей базой данных, то есть индексы тут не помогут. Например если у Гугла поисковая база 100 терабайт, но нужно будет выполнить вычисления над запросом и всей базой.
Пример:
Клиент хочет узнать если ли слово (число) x в множестве А, которое известно серверу, но не хочет что бы сервер узнал x. Сам он множество А не знает.
Клиент отправляет $f(x)$ на сервер. Сервер считает $prod(f(x)-y | y in A) = prod(f(x-y) | y in A) = f(prod(x-y | y in A))$, здесь мы пользуемся гомоморфностью относительно сложения и умножения одновременно. Теперь это значение получает клиент, снимает шифрование и получает нулевое или не нулевое значение, по которому узнает ответ. (нулевое значение почти всегда означает что слово есть в множестве)
Если библиотека не даёт сделать $y -> f(y)$, то клиент может отправить ${b_i = f(2^i) | 0 <= i < N}$, тогда сервер может получить любую константу сложением $n < 2^N -> f(n) = f(sum(2^e | e in B)) = sum(f(2^e | e in B)) = sum(b_e | e in B)$, где B двоичное представление n.
Ну или наивный Байес, тут еще проще. Отправляем ${f(p_w) | w in U}$, bag of words,
Сервер возвращает линейную комбинацию $sum(a_w f(p_w) | w in U) =… = f(sum(a_w p_w | w in U))$. В итоге сервер не знает письма, а клиент не знает коэффициентов, все очень просто.
При желании можно и нейронку на таком входе посчитать, все упирается в функцию активации, для логистической можно экспоненту в ряд Тейлора разложить до какого-то члена, и должно нормально получиться, ну еще и делить придётся.
Естественно f должна меняться при каждом письме, иначе двух запросов с разными p_w и одинаковыми остальными значениями будет достаточно для того что бы узнать одно a_w.
Для того что бы работать с длинными словами, можно отправлять ${f(x_i) | 0 <= i < W}$, и перемножать $sum(f((x_i — y_i)^2) | 0 <= i < W)$, (вместо $(x-y)$) но тогда клиент раскрывает часть информации об $x$, но тем меньшую, чем больший размер слова доступен, и чего можно совсем избежать если преобразовать слова по принципу '{s_1,s_2,s_3} -> {(1,s_1),(2,s_2),(3,s_3)}'.
Fullmoon
Ну, навскидку: есть подстрока, сигнализирующая о спаме, мы вычисляем, как бы выглядел зашифрованный текст, в котором эта подстрока находится на позиции n.
Впрочем, может быть и пример надуманный, да.
anonymous
Ну для начала нужен критерий того что такое спам. Условно говоря, есть функция f(x), которая возвращает вероятность того что это спам. Эта функция выполняет вычисления над x. Вычисления в f(x) можно провести гомоморфно, а результат вычислений передать тому, кто имеет право расшифровывать сообщения. Он расшифровывает результат и на основе полученной вероятности принимает решение. Это может быть владелец почты. Кода он подключается к почтовому ящику, то ему передаются шифротексты с вероятностями спама и на его стороне происходит расшифрование.
putinBog
«Предположим, что Алиса является владельцем ювелирного магазина. Рабочие Алисы должны сделать из заготовок ювелирные изделия. Но Алису беспокоит кража. Как рабочие могут выполнять работу, не имея прямого доступа к драгоценностям? Алиса помещает заготовки в запертый ящик, ключ от которого есть только у нее. Рабочие собирают украшение прямо в коробке (используйте фантазию). Алиса потом отпирает коробку, чтобы получить результат.»(с)
Математически задача выглядит как преобразование данных в зашифрованные блоки, над которыми можно производить простые арифметические операции, результаты которых сможет декодировать владелец ключа.
То есть письмо преобразуется в некий набор микрошифров, которые сможет прожевать нейросеть на недоверенном сервере, вычислить какой-то результат, но смысл результата останется тайной для владельца сервера. Только клиент, расшифровав результат своим ключом, сможет интерпретировать оценку как «спам-не спам». Понял так
panvartan
Алиса делает в коробочке в нужных местах дырочки, через которые пальцы рабочих смогут обработать заготовку до состояния изделия, но не смогут вытащить ни заготовку, ни изделие целиком. Очевидно, за этим будущее, но пока это сильно усложняет обработку — примерно в «триллион раз»
engine9
Похоже на химический шкаф с вытяжкой и встроенными резиновыми перчатками.
AC130
Ну гомоморфное шифрование из статьи позволяет к произвольному набору чисел применить некую функцию, выражающуюся в виде последовательности сложений и умножений над этим набором чисел, так, что входной набор чисел и результат вычисления неизвестны тому, кто эту функцию применяет (так как эти данные зашифрованы), а сама функция неизвестна тому, чьи данные обрабатываются.
Если вы можете операцию детектирования спама в письме выразить как набор сложений и умножений над числами, однозначно соответствующими этому письму, то вот это оно и есть.
Undiabler
К примеру реализация спам фильтра razor2. Идея заключается в том что все письмо дробится на маленькие кусочки и каждый из кусочков преобразуется в хеш (по аналогии с торрентами). Таким образом мы можем составить карту хешей и их рейтинг. Если в письме находится много хешей с плохим рейтингом — письмо спамовое.
Проблема razor в том что вычислять хеш нужно в неком доверенном месте, ну или определять является ли письмо спамом в момент открытия пользовательстким клиентом, что так же накладывает массу условий.
В случае с гомоморфным шифрованием можно убрать эти проблемы вычисляя хеши по зашифрованным данным.
EzikBro
Идея такая:
Пусть у нас есть модель-классификатор, которая определяет, является ли сообщение спамом. У нас есть датасет, на котором ее обучили, все настройки и все такое.
Далее мы шифруем все эти данные и обучаем новую модель на зашифрованных данных. Теперь у нас есть вторая модель, которая умеет работать только с зашифрованными сообщениями.
И теперь результаты первой модели на незашифрованных сообщениях будут почти полностью совпадать с результатами второй модели на тех же самых, но зашифрованных сообщениях.
И при этом вторая модель даже знать не может, какое это было сообщение изначально.