Проблемы информационной безопасности требуют изучения и решения ряда теоретических и практических задач при информационном взаимодействии абонентов систем. В нашей доктрине информационной безопасности формулируется триединая задача обеспечения целостности, конфиденциальности и доступности информации. Представляемые здесь статьи посвящаются рассмотрению конкретных вопросов ее решения в рамках разных государственных систем и подсистем. Ранее автором были рассмотрены в 5 статьях вопросы обеспечения конфиденциальности сообщений средствами государственных стандартов. Общая концепция системы кодирования также приводилась мной ранее.

Введение

По основному своему образованию я не математик, но в связи с читаемыми мной дисциплинами в ВУЗе пришлось в ней дотошно разбираться. Долго и упорно читал классические учебники ведущих наших Университетов, пятитомную математическую энциклопедию, множество тонких популярных брошюр по отдельным вопросам, но удовлетворения не возникало. Не возникало и глубокое понимание прочитанного.

Вся математическая классика ориентирована, как правило, на бесконечный теоретический случай, а специальные дисциплины опираются на случай конечных конструкций и математических структур. Отличие подходов колоссальное, отсутствие или недостаток хороших полных примеров — пожалуй главный минус и недостаток вузовских учебников. Очень редко существует задачник с решениями для начинающих (для первокурсников), а те, что имеются, грешат пропусками в объяснениях. В общем я полюбил букинистические магазины технической книги, благодаря чему пополнилась библиотека и в определенной мере багаж знаний. Читать довелось много, очень много, но «не заходило».

Этот путь привел меня к вопросу, а что я уже могу самостоятельно делать без книжных «костылей», имея перед собой только чистый лист бумаги и карандаш с ластиком? Оказалось совсем немного и не совсем то, что было нужно. Пройден был сложный путь бессистемного самообразования. Вопрос был такой. Могу ли я построить и объяснить, прежде всего себе, работу кода, обнаруживающего и исправляющего ошибки, например, код Хемминга, (7, 4)-код?

Известно, что код Хемминга широко используется во многих прикладных программах в области хранения и обмена данными, особенно в RAID; кроме того, в памяти типа ECC и позволяет «на лету» исправлять однократные и обнаруживать двукратные ошибки.

Информационная безопасность. Коды, шифры, стегосообщения

Информационное взаимодействие путем обмена сообщениями его участников должно обеспечиваться защитой на разных уровнях и разнообразными средствами как аппаратными так и программными. Эти средства разрабатываются, проектируются и создаются в рамках определенных теорий (см. рис.А) и технологий, принятых международными договоренностями об OSI/ISO моделях.

Защита информации в информационных телекоммуникационных системах (ИТКС) становится практически основной проблемой при решении задач управления, как в масштабе отдельной личности – пользователя, так и для фирм, объединений, ведомств и государства в целом. Из всех аспектов защиты ИТКС в этой статье будем рассматривать защиту информации при ее добывании, обработке, хранении и передаче в системах связи.

Уточняя далее предметную область, остановимся на двух возможных направлениях, в которых рассматриваются два различных подхода к защите, представлению и использованию информации: синтаксическом и семантическом. На рисунке используются сокращения: кодек–кодер-декодер; шидеш – шифратор-дешифратор; скриз – скрыватель – извлекатель.


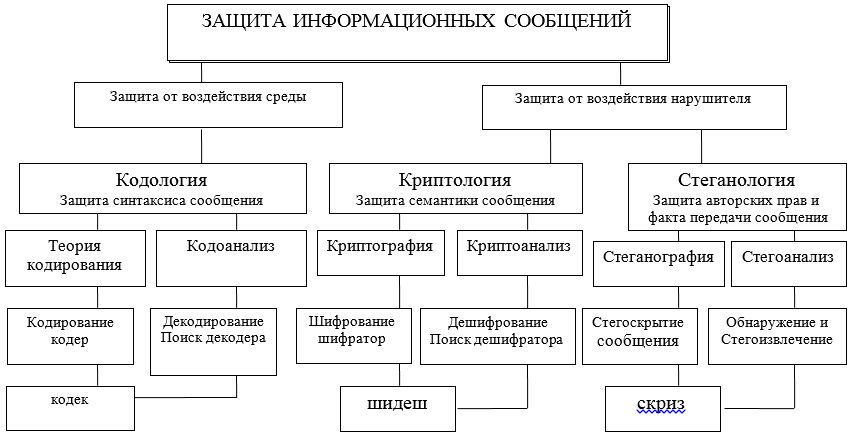
Рисунок А – Схема основных направлений и взаимосвязи теорий, направленных на решение задач защиты информационного взаимодействия

Синтаксические особенности представления сообщений позволяют контролировать и обеспечивать правильность и точность (безошибочность, целостность) представления при хранении, обработке и особенно при передаче информации по каналам связи. Здесь главные задачи защиты решаются методами кодологии, ее большой части — теории корректирующих кодов.

Семантическая (смысловая) безопасность сообщений обеспечивается методами криптологии, которая средствами криптографии позволяет защитить от овладения содержанием информации потенциальным нарушителем. Нарушитель при этом может скопировать, похитить, изменить или подменить, или даже уничтожить сообщение и его носитель, но он не сможет получить сведений о содержании и смысле передаваемого сообщения. Содержание информации в сообщении останется для нарушителя недоступным. Таким образом, предметом дальнейшего рассмотрения будет синтаксическая и семантическая защита информации в ИТКС. В этой статье ограничимся рассмотрением только синтаксического подхода в простой, но весьма важной его реализации корректирующим кодом.

Сразу проведу разграничительную линию в решении задач информационной безопасности:
теория кодологии призвана защищать информацию (сообщения) от ошибок (защита и анализ синтаксиса сообщений) канала и среды, обнаруживать и исправлять ошибки;
теория криптологии призвана защищать информацию от несанкционированного доступа к ее семантике нарушителя (защита семантики, смысла сообщений);
теория стеганологии призвана защищать факт информационного обмена сообщениями, а также обеспечивать защиту авторского права, персональных данных (защита врачебной тайны).

В общем «поехали». По определению, а их довольно много, понять что есть код очень даже не просто. Авторы пишут, что код — это алгоритм, отображение и ещё что-то. О классификации кодов я не буду здесь писать, скажу только, что (7, 4)-код блоковый.

В какой-то момент до меня дошло, что код — это кодовые специальные слова, конечное их множество, которыми заменяют специальными алгоритмами исходный текст сообщения на передающей стороне канала связи и которые отправляются по каналу получателю. Замену осуществляет устройство-кодер, а на приемной стороне эти слова распознает устройство-декодер.

Поскольку роль сторон переменчива оба этих устройства объединяют в одно и называют сокращенно кодек (кодер/декодер), и устанавливают на обоих концах канала. Дальше, раз есть слова, есть и алфавит. Алфавит — это два символа {0, 1}, в технике массово используются блоковые двоичные коды. Алфавит естественного языка (ЕЯ) — множество символов — букв, заменяющих при письме звуки устной речи. Здесь не будем углубляться в иероглифическую письменность в слоговое или узелковое письмо.

Алфавит и слова — это уже язык, известно, что естественные человеческие языки избыточны, но что это означает, где обитает избыточность языка трудно сказать, избыточность не очень хорошо организована, хаотична. При кодировании, хранении информации избыточность стремятся уменьшить, пример, архиваторы, код Морзе и др.

Ричард Хемминг, наверное, раньше других понял, что если избыточность не устранять, а разумно организовать, то ее можно использовать в системах связи для обнаружения ошибок и автоматического их исправления в кодовых словах передаваемого текста. Он понял, что все 128 семиразрядных двоичных слов могут использоваться для обнаружения ошибок в кодовых словах, которые образуют код — подмножество из 16 семиразрядных двоичных слов. Это была гениальная догадка.

До изобретения Хемминга ошибки приемной стороной тоже обнаруживались, когда декодированный текст не читался или получалось не совсем то, что нужно. При этом посылался запрос отправителю сообщения повторить блоки определенных слов, что, конечно, было весьма неудобно и тормозило сеансы связи. Это было большой не решаемой десятилетиями проблемой.

Построение (7, 4)-кода Хемминга

Вернемся к Хеммингу. Слова (7, 4)-кода образованы из 7 разрядов С j = $$, j = 0(1)15, 4-информационные и 3-проверочные символа, т.е. по существу избыточные, так как они не несут информации сообщения. Эти три проверочных разряда удалось представить линейными функциями 4-х информационных символов в каждом слове, что и обеспечило обнаружение факта ошибки и ее места в словах, чтобы внести исправление. А (7, 4)-код получил новое прилагательное и стал линейным блоковым двоичным.

Линейные функциональные зависимости (правила (*)) вычислений значений символов
$$ имеют следующий вид:

$$
$$
$$

Исправление ошибки стало очень простой операцией — в ошибочном разряде определялся символ (ноль или единица) и заменялся другим противоположным 0 на 1 или 1 на 0.
Сколько же различных слов образуют код? Ответ на этот вопрос для (7, 4)-кода получается очень просто. Раз имеется лишь 4 информационных разряда, а их разнообразие при заполнении символами имеет $$ = 16 вариантов, то других возможностей просто нет, т. е. код состоящий всего из 16 слов, обеспечивает представление этими 16-ю словами всю письменность всего языка.

Информационные части этих 16 слов получают нумерованный вид №
($$):

0=0000; 4= 0100; 8=1000; 12=1100;
1=0001; 5= 0101; 9=1001; 13=1101;
2=0010; 6= 0110; 10=1010; 14=1110;
3=0011; 7= 0111; 11=1011; 15=1111.

Каждому из этих 4-разрядных слов необходимо вычислить и добавить справа по 3 проверочных разряда, которые вычисляются по правилам (*). Например, для информационного слова №6 равного 0110 имеем $$ и вычисления проверочных символов дают для этого слова такой результат:

$$
$$
$$
$$

Шестое кодовое слово при этом приобретает вид: $$ Таким же образом необходимо вычислить проверочные символы для всех 16-и кодовых слов. Подготовим для слов кода 16-строчную таблицу К и последовательно будем заполнять ее клетки (читателю рекомендую проделать это с карандашом в руках).

Таблица К – кодовые слова Сj, j = 0(1)15, (7, 4) – кода Хемминга

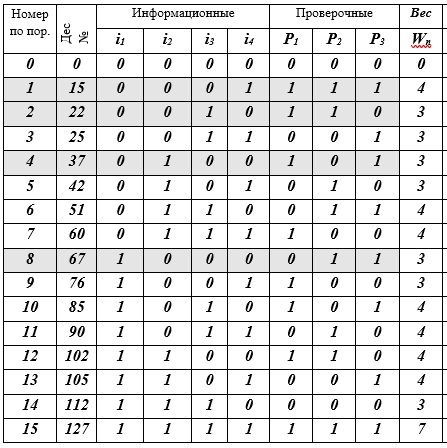
Описание таблицы: 16 строк — кодовые слова; 10 колонок: порядковый номер, десятичное представление кодового слова, 4 информационных символа, 3 проверочных символа, W-вес кодового слова равен числу ненулевых разрядов (? 0). Заливкой выделены 4 кодовых слова-строки — это базис векторного подпространства. Собственно, на этом все — код построен.

Таким образом, в таблице получены все слова (7, 4) — кода Хемминга. Как видите это было не очень сложно. Далее речь пойдет о том, какие идеи привели Хемминга к такому построению кода. Мы все знакомы с кодом Морзе, с флотским семафорным алфавитом и др. системами построенными на разных эвристических принципах, но здесь в (7, 4)-коде используются впервые строгие математические принципы и методы. Рассказ будет как раз о них.

Математические основы кода. Высшая алгебра

Подошло время рассказать какая Р.Хеммингу пришла идея открытия такого кода. Он не питал особых иллюзий о своем таланте и скромно формулировал перед собой задачу: создать код, который бы обнаруживал и исправлял в каждом слове одну ошибку (на деле обнаруживать удалось даже две ошибки, но исправлялась лишь одна из них). При качественных каналах даже одна ошибка — редкое событие. Поэтому замысел Хемминга все-таки в масштабах системы связи был грандиозным. В теории кодирования после его публикации произошла революция.

Это был 1950 год. Я привожу здесь свое простое (надеюсь доступное для понимания) описание, которого не встречал у других авторов, но как оказалось, все не так просто. Потребовались знания из многочисленных областей математики и время, чтобы все глубоко осознать и самому понять, почему это так сделано. Только после этого я смог оценить ту красивую и достаточно простую идею, которая реализована в этом корректирующем коде. Время я в основном, потратил на разбирательство с техникой вычислений и теоретическим обоснованием всех действий, о которых здесь пишу.

Создатели кодов, долго не могли додуматься до кода, обнаруживающего и исправляющего две ошибки. Идеи, использованные Хеммингом, там не срабатывали. Пришлось искать, и нашлись новые идеи. Очень интересно! Захватывает. Для поиска новых идей потребовалось около 10 лет и только после этого произошел прорыв. Коды, обнаруживающие произвольное число ошибок, были получены сравнительно быстро.

Векторные пространства, поля и группы. Полученный (7, 4)-код (Таблица К) представляет множество кодовых слов, являющихся элементами векторного подпространства (порядка 16, с размерностью 4), т.е. частью векторного пространства размерности 7 с порядком $$ Из 128 слов в код включены лишь 16, но они попали в состав кода не просто так.

Во-первых, они являются подпространством со всеми вытекающими отсюда свойствами и особенностями, во-вторых, кодовые слова являются подгруппой большой группы порядка 128, даже более того, аддитивной подгруппой конечного расширенного поля Галуа GF($$) степени расширения n = 7 и характеристики 2. Эта большая подгруппа раскладывается в смежные классы по меньшей подгруппе, что хорошо иллюстрируется следующей таблицей Г. Таблица разделена на две части: верхняя и нижняя, но читать следует как одну длинную. Каждый смежный класс (строка таблицы) — элемент факторгруппы по эквивалентности составляющих.

Таблица Г – Разложение аддитивной группы поля Галуа GF ($$) в смежные классы (строки таблицы Г) по подгруппе 16 порядка.

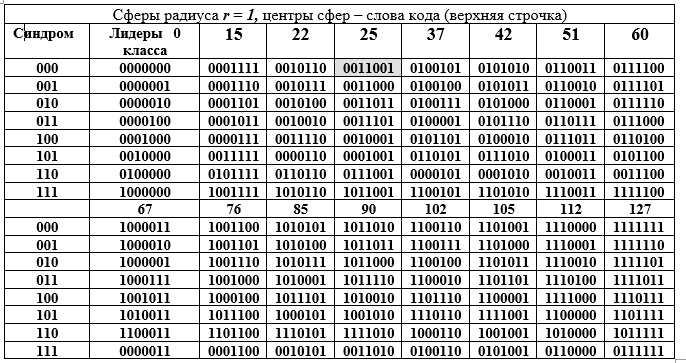
Столбцы таблицы – это сферы радиуса 1. Левый столбец (повторяется) – синдром слова (7, 4)-кода Хемминга, следующий столбец — лидеры смежного класса. Раскроем двоичное представление одного из элементов (25-го выделен заливкой) факторгруппы и его десятичное представление:

$$

Техника получение строк таблицы Г. Элемент из столбца лидеров класса суммируется с каждым элементом из заголовка столбца таблицы Г (суммирование выполняется для строки лидера в двоичном виде по mod2). Поскольку все лидеры классов имеют вес W=1, то все суммы отличаются от слова в заголовке столбца только в одной позиции (одной и той же для всей строки, но разных для столбца). Таблица Г имеет замечательную геометрическую интерпретацию. Все 16 кодовых слов представляются центрами сфер в 7-мерном векторном пространстве. Все слова в столбце от верхнего слова отличаются в одной позиции, т. е. лежат на поверхности сферы с радиусом r =1.

В этой интерпретации скрывается идея обнаружения одной ошибки в любом кодовом слове. Работа идет со сферами. Первое условие обнаружения ошибки — сферы радиуса 1 не должны касаться или пересекаться. Это означает, что центры сфер удалены друг от друга на расстояние 3 или более. При этом сферы не только не пересекаются, но и не касаются одна другой. Это требование для однозначности решения: какой сфере отнести полученное на приемной стороне декодером ошибочное (не кодовое одно из 128 -16 = 112) слово.

Второе — все множество 7-разрядных двоичных слов из 128 слов равномерно распределено по 16 сферам. Декодер может получить слово лишь из этого множества 128-ми известных слов с ошибкой или без нее. Третье — приемная сторона может получить слово без ошибки или с искажением, но всегда принадлежащее одной из 16-и сфер, которая легко определяется декодером. В последней ситуации принимается решение о том, что послано было кодовое слово — центр определенной декодером сферы, который нашел позицию (пересечение строки и столбца) слова в таблице Г, т. е номера столбца и строки.

Здесь возникает требование к словам кода и к коду в целом: расстояние между любыми двумя кодовыми словами должно быть не менее трех, т. е. разность для пары кодовых слов, например, Сi = 85=$$=1010101; Сj = 25=$$= 0011001 должна быть не менее 3; 85 — 25 = 1010101 — 0011001 =1001100 = 76, вес слова-разности W(76) = 3. (табл. Д заменяет вычисления разностей и сумм). Здесь под расстоянием между двоичными словами-векторами понимается количество не совпадающих позиций в двух словах. Это расстояние Хемминга, которое стало повсеместно использоваться в теории, и на практике, так как удовлетворяет всем аксиомам расстояния.

Замечание. (7, 4)-код не только линейный блоковый двоичный, но он еще и групповой, т. е. слова кода образуют алгебраическую группу по сложению. Это означает, что любые два кодовых слова при суммировании снова дают одно из кодовых слов. Только это не обычная операция суммирования, выполняется сложение по модулю два.

Таблица Д — Сумма элементов группы (кодовых слов), используемой для построения кода Хемминга

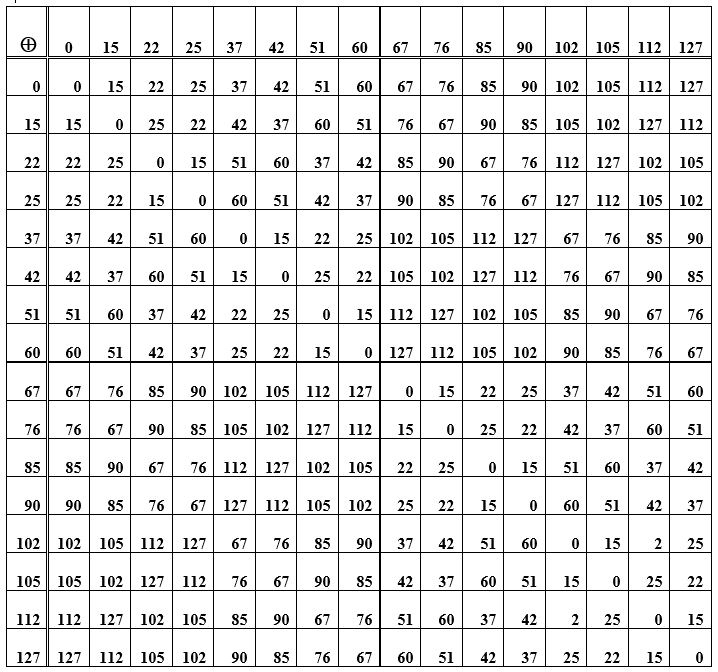
Сама операция суммирования слов ассоциативна, и для каждого элемента в множестве кодовых слов имеется противоположный ему, т. е. суммирование исходного слова с противоположным дает нулевое значение. Это нулевое кодовое слово является нейтральным элементом в группе. В таблице Д- это главная диагональ из нулей. Остальные клетки (пересечения строка/столбец) — это номера-десятичные представления кодовых слов, полученные суммированием элементов из строки и столбца.При перестановке слов местами (при суммировании) результат остается прежним, более того, вычитание и сложение слов имеют одинаковый результат. Дальше рассматривается система кодирования/декодирования, реализующая синдромный принцип.

Применение кода. Кодер

Кодер размещается на передающей стороне канала и им пользуется отправитель сообщения. Отправитель сообщения (автор) формирует сообщение в алфавите естественного языка и представляет его в цифровом виде. (Имя символа в ASCII-соде и в двоичном виде).
Тексты удобно формировать в файлах для ПК с использованием стандартной клавиатуры (ASCII — кодов). Каждому символу (букве алфавита) соответствует в этой кодировке октет бит (восемь разрядов). Для (7, 4)- кода Хемминга, в словах которого только 4 информационных символа, при кодировании символа клавиатуры на букву требуется два кодовых слова, т.е. октет буквы разбивается на два информационных слова естественного языка (ЕЯ) вида
$$.

Пример 1. Необходимо передать слово «цифра» в ЕЯ. Входим в таблицу ASCII-кодов, буквам соответствуют: ц –11110110, и –11101000, ф – 11110100, р – 11110000, а – 11100000 октеты. Или иначе в ASCII — кодах слово «цифра» = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000

с разбивкой на тетрады (по 4 разряда). Таким образом, кодирование слова «цифра» ЕЯ требует 10 кодовых слов (7, 4)-кода Хемминга. Тетрады представляют информационные разряды слов сообщения. Эти информационные слова (тетрады) преобразуются в слова кода (по 7 разрядов) перед отправкой в канал сети связи. Выполняется это путем векторно-матричного умножения: информационного слова на порождающую матрицу. Плата за удобства получается весьма дорого и длинно, но все работает автоматически и главное — сообщение защищается от ошибок.
Порождающая матрица (7, 4)-кода Хемминга или генератор слов кода получается выписыванием базисных векторов кода и объединением их в матрицу. Это следует из теоремы линейной алгебры: любой вектор пространства (подпространства) является линейной комбинацией базисных векторов, т.е. линейно независимых в этом пространстве. Это как раз и требуется — порождать любые векторы (7-разрядные кодовые слова) из информационных 4-разрядных.

Порождающая матрица (7, 4, 3)-кода Хемминга или генератор слов кода имеет вид:


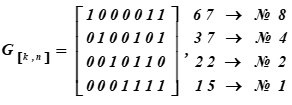
Справа указаны десятичные представления кодовых слов Базиса подпространства и их порядковые номера в таблице К
№ i строки матрицы — это слова кода, являющиеся базисом векторного подпространства.

Пример кодирования слов информационных сообщений (порождающая матрица кода выстраивается из базисных векторов и соответствует части таблицы К). В таблице ASCII-кода берем букву ц = <1111 0110>.

Информационные слова сообщения имеют вид:

$$.

Это половины символа (ц). Для (7, 4)-кода, определенного ранее, требуется найти кодовые слова, соответствующее информационному слову-сообщению (ц) из 8-и символов в виде:

$$.

Чтобы превратить эту букву–сообщение (ц) в кодовые слова u, каждую половинку буквы-сообщения i умножают на порождающую матрицу G[k, n] кода (матрица для таблицы К):



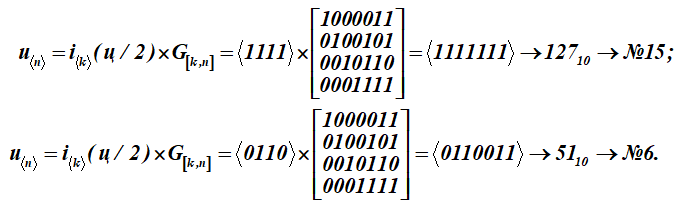
Получили два кодовых слова с порядковыми номерами 15 и 6.

Покажем детальное формирование нижнего результата №6 – кодового слова (умножение строки информационного слова на столбцы порождающей матрицы); суммирование по (mod2)

<0110> • <1000> = 0•1 +1•0 + 1•0 + 0•0 = 0(mod2);
<0110> • <0100> = 0•0 +1•1 + 1•0 + 0•0 = 1(mod2);
<0110> • <0010> = 0•0 +1•0 + 1•1 + 0•0 = 1(mod2);
<0110> • <0001> = 0•0 +1•0 + 1•0 + 0•1 = 0(mod2);
<0110> • <0111> = 0•0 +1•1 + 1•1 + 0•1 = 0(mod2);
<0110> • <1011> = 0•1 +1•0 + 1•1 + 0•1 = 1(mod2);
<0110> • <1101> = 0•1 +1•1 + 1•0 + 0•1 = 1(mod2).

Получили в результате перемножения пятнадцатое и шестое слова из таблицы К. Первые четыре разряда в этих кодовых словах (результатах умножения) представляют информационные слова. Они имеют вид: $$, (в таблице ASCII это только половины буквы ц). Для кодирующей матрицы выбраны в качестве базисных векторов в таблице К совокупности слов с номерами: 1, 2, 4, 8. В таблице они выделены заливкой. Тогда для этой таблицы К кодирующая матрица получит вид G[k,n].

В результате перемножения получили 15 и 6 слова таблицы К кода.

Применение кода. Декодер

Декодер размещается на приемной стороне канала там, где находится получатель сообщения. Назначение декодера состоит в предоставлении получателю переданного сообщения в том виде, в котором оно существовало у отправителя в момент отправления, т.е. получатель может воспользоваться текстом и использовать сведения из него для своей дальнейшей работы.

Основной задачей декодера является проверка того, является ли полученное слово (7 разрядов) тем, которое было отправлено на передающей стороне, не содержит ли слово ошибок. Для решения этой задачи для каждого полученного слова декодером путем умножения его на проверочную матрицу Н[n-k, n] вычисляется короткий вектор-синдром S (3 разряда).

Для слов, которые являются кодовыми, т. е. не содержат ошибок, синдром всегда принимает нулевое значение S =<000>. Для слова с ошибкой синдром не нулевой S ? 0. Значение синдрома позволяет обнаружить и локализовать положение ошибки с точностью до разряда в принятом на приемной стороне слове, и декодер может изменить значение этого разряда. В проверочной матрице кода декодер находит столбец, совпадающий со значением синдрома, и порядковый номер этого столбца принимает равным искаженному ошибкой разряду. После этого для двоичных кодов декодером выполняется изменение этого разряда – просто замена на противоположное значение, т. е. единицу заменяют нулем, а нуль – единицей.

Рассматриваемый код является систематическим, т. е. символы информационного слова размещаются подряд в старших разрядах кодового слова. Восстановление информационных слов выполняется простым отбрасыванием младших (проверочных) разрядов, число которых известно. Далее используется таблица ASCII-кодов в обратном порядке: входом являются информационные двоичные последовательности, а выходом – буквы алфавита естественного языка. Итак, (7, 4)-код систематический, групповой, линейный, блочный, двоичный.

Основу декодера образует проверочная матрица Н[n-k, n], которая содержит число строк, равное числу проверочных символов, а столбцами все возможные, кроме нулевого, столбцы из трех символов $$. Проверочная матрица строится из слов таблицы К, они выбираются так, чтобы быть ортогональными к кодирующей матрице, т.е. их произведение — нулевая матрица. Проверочная матрица получает следующий вид в операциях умножения она транспонируется. Для конкретного примера проверочная матрица Н[n-k, n] приведена ниже:





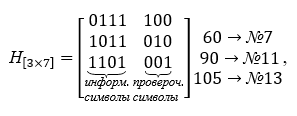
Видим, что произведение порождающей матрицы на проверочную в результате дает нулевую матрицу.

Пример 2. Декодирование слова кода Хемминга без ошибки (е<7> =<0000000>).
Пусть на приемном конце канала приняты слова №7>60 и №13>105 из таблицы К,
u<7> + е<7> = <0 1 1 1 1 0 0 > + <0 0 0 0 0 0 0>,
где ошибка отсутствует, т. е. имеет вид е<7> = <0 0 0 0 0 0 0>.


В результате вычисленный синдром имеет нулевое значение, что подтверждает отсутствие ошибки в словах кода.

Пример 3. Обнаружение одной ошибки в слове, полученном на приемном конце канала (таблица К).

А) Пусть требуется передать 7 – е кодовое слово, т.е.

u<7> = <0 1 1 1 1 0 0> и в одном третьем слева разряде слова, допущена ошибка. Тогда она суммируется по mod2 с 7-м передаваемым по каналу связи кодовым словом
u<7> + е<7> = <0 1 1 1 1 0 0 > + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0>,
где ошибка имеет вид е<7> = <0 0 1 0 0 0 0>.

Установление факта искажения кодового слова выполняется умножением полученного искаженного слова на проверочную матрицу кода. Результатом такого умножения будет вектор, называемый синдромом кодового слова.

Выполним такое умножение для наших исходных (7-го вектора с ошибкой) данных.


В результате такого умножения на приемном конце канала получили вектор-синдром S<n-k>, размерность которого (n–k). Если синдром S<3>= <0,0,0> нулевой, то делается вывод о том, что принятое на приемной стороне слово принадлежит коду С и передано без искажений. Если синдром не равен нулю S<3> ? <0,0,0>, то его значение указывает на наличие ошибки и ее место в слове. Искаженный разряд соответствует номеру позиции столбца матрицы Н[n-k, n], совпадающего с синдромом. После этого искаженный разряд исправляется, и полученное слово обрабатывается декодером далее. На практике для каждого принятого слова сразу вычисляется синдром и при наличии ошибки, она автоматически устраняется.

Итак, при вычислениях получен синдром S=<110> для обоих слов одинаковый. Смотрим на проверочную матрицу и отыскиваем в ней столбец, совпадающий с синдромом. Это третий слева столбец. Следовательно, ошибка допущена в третьем слева разряде, что совпадает с условиями примера. Этот третий разряд изменяется на противоположное значение и мы вернули принятые декодером слова к виду кодовых. Ошибка обнаружена и исправлена.

Вот собственно и все, именно так устроен и работает классический (7, 4)-код Хемминга.

Здесь не рассматриваются многочисленные модификации и модернизации этого кода, так как важны не они, а те идеи и их реализации, которые в корне изменили теорию кодирования, и как следствие, системы связи, обмена информацией, автоматизированные системы управления.

Заключение

В работе рассмотрены основные положения и задачи информационной безопасности, названы теории, призванные решать эти задачи.

Задача защиты информационного взаимодействия субъектов и объектов от ошибок среды и от воздействий нарушителя относится к кодологии.

Рассмотрен в деталях (7, 4)-код Хемминга, положивший начало нового направлению в теории кодирования — синтеза корректирующих кодов.

Показано применение строгих математических методов, используемых при синтезе кода.
Приведены примеры иллюстрирующие работоспособность кода.

Литература

Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. М.: Мир, 1976, 594 c.
Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер.с англ. М.: Мир, 1986, 576 с.