20.08.2020 13:32
BuddhaSugata 88 4100 Источник
Habritants! В этой статье описано получение метрики общего вида, включающей метрики Фридмана и Шварцшильда как частные случаи.

Для понимания материала необходимо понятие о производных.

Представим, что у пространства есть четвёртое измерение. Как если бы движение в нём забирало у объекта некоторое количество движения или наоборот. Словно гравитация это чисто геометрический эффект создания субпространственной воронки вокруг любого объекта, обладающего энергией.

Вы наверняка натыкались на подобную визуализацию гравитации, если интересуетесь вопросом:

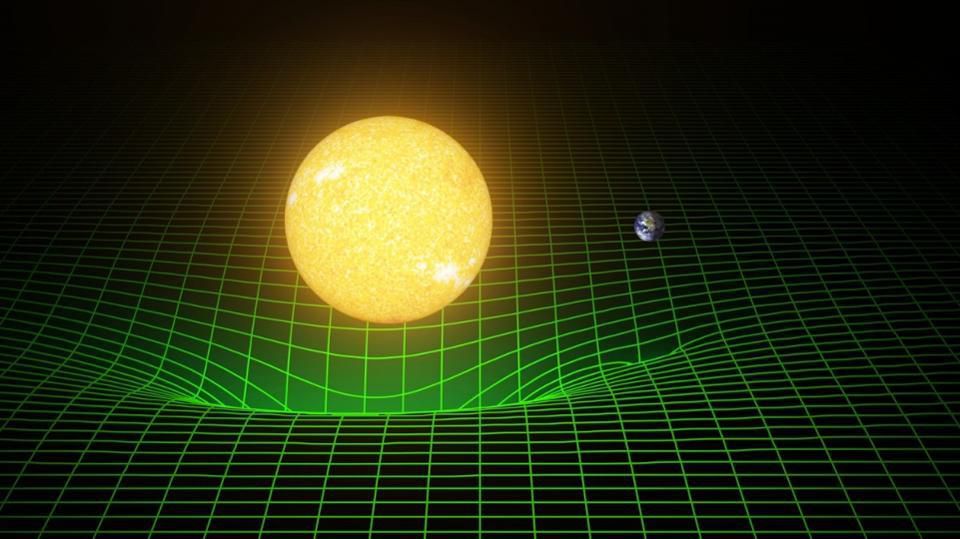
image

Для того, чтобы оценить глубину такой воронки и механизм взаимодействия объектов, сформулируем выражение интервала сигнатуры (1-4).

3-сферические координаты


Представим 4-ёх мерное пространство $\psi (w,x,y,z) = \mathbb{R}^4$, и зададим в нём сферические координаты $(r, \theta, \phi, \eta)$:

$] \, {w = r\sin\theta\sin\phi\cos\eta; \\ x = r\sin\theta\sin\phi\sin\eta; \\ y = r\sin\theta\cos\phi; \\ z = r\cos\theta } \\$


Для этого запишем переходную матрицу:

$\vec{r} = \left( \matrix{w \\ x \\ y \\ z} \right) = \left( \matrix{r\sin\theta\sin\phi\cos\eta \\ r\sin\theta\sin\phi\sin\eta \\ r\sin\theta\cos\phi \\ r\cos\theta } \right) $


Посчитаем переходные коэффициенты:

$ g_r = \left| \frac{\partial\vec{r}}{\partial r} \right| = \sqrt{ \left( \frac{\partial w}{\partial r} \hat{h} + \frac{\partial x}{\partial r} \hat{i} + \frac{\partial y}{\partial r} \hat{j} + \frac{\partial z}{\partial r} \hat{k} \right)^2 } = \\ = \sqrt{sin^2\theta\sin^2\phi\cos^2\eta + \sin^2\theta\sin^2\phi\sin^2\eta + sin^2\theta\cos^2\phi + \cos^2\theta} = 1 \\ g_\theta = \left| \frac{\partial\vec{r}}{\partial \theta} \right| = \sqrt{r^2cos^2\theta\sin^2\phi\cos^2\eta+r^2\cos^2\theta\sin^2\phi\sin^2\eta+r^2\cos^2\theta\cos^2\phi+r^2sin^2\theta} = \\ = \sqrt{r^2(sin^2\theta + \cos^2\theta (cos^2\phi + sin^2\phi (cos^2\eta+sin^2\eta)))} = r \\ g_\phi = \left| \frac{\partial\vec{r}}{\partial \phi} \right| = \sqrt{r^2sin^2\theta\cos^2\phi\cos^2\eta + r^2sin^2\theta\cos^2\phi\sin^2\eta + r^2sin^2\theta\sin^2\phi + 0} = \\ = \sqrt{r^2sin^2\theta} = r\sin\theta \\ g_\eta = \left| \frac{\partial\vec{r}}{\partial \eta} \right| = \sqrt{r^2\sin^2\theta\sin^2\phi\sin^2\eta+r^2\sin^2\theta\sin^2\phi\cos^2\eta} = r\sin\theta\sin\phi $


И представим соответствующий $\psi$ интервал:

$ds^2 = \color{red}{(-1)\cdot dt^2} + (dw^2 + \color{green}{ dx^2 + dy^2 + dz^2}) \\ ds^2 = (-1)\cdot dt^2 + (g_r^2 dr^2 + g_\theta^2 d\theta^2 + g_\phi^2 d\phi^2 + g_\eta^2 d\eta^2) \\ ds^2 = (-1)\cdot dt^2 + 1 \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2 + r^2 \cdot \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 \\ ds^2 = \color{red}{(-1)\cdot dt^2} + \color{magenta}{1 \cdot dr^2} + \color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 \right)}$


Красным — темпоральная составляющая, представленная аналогично метрике FLRW.
Зелёным — пространственная составляющая, представленная аналогично метрике FLRW, и представляющая собой поверхность 3-сферы.

Маджента получилась подвисшим между временем и пространством звеном — дифференциалом изменения мультипликатора пространственной части.

Общий вид интервала


Продолжая развитие идей, изложенных в предыдущей статье, положим изменение четвёртого измерения мерой связанной с относительным количеством энергии объектов, следовательно, дополним метрику составляющей $\color{orange}{-dr^2}$ в силу рассмотрения энергетически замкнутой системы, что будет предполагаться истинным и для Вселенной в целом (решение Фридмана), и для сферически симметричного массивного тела (решение Шварцшильда). Читатель не согласный с такой трактовкой, может просто считать это математическим трюком:

$ds^2 = \color{red}{(-1)\cdot dt^2 \left( 1 - \color{magenta}{\frac{dr^2}{dt^2}} \right)} + \color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 - \color{orange}{\frac{dr^2}{r^2}} \right)}$


Маджента в темпоральной части понятна:

$\color{magenta}{ \frac{dr^2}{dt^2} = \dot{r}^2 }$


Зелёную переформируем, чтобы показать, что пространство $\psi'(\theta, \phi, \eta) = \mathbb{R}^3 \in \psi$ можно представить в угловых координатах $(x_1, y_1, z_1)$ подобно метрике FLRW:

$\color{green}{r^2 \left( d\theta^2 + \sin^2\theta \cdot d\phi^2 + \sin^2\theta \cdot \sin^2\phi \cdot d\eta^2 - \color{orange}{\frac{dr^2}{r^2}} \right) = \\ = r^2 \cdot dx_1^2 + r^2 \cdot \sin^2\theta \cdot \frac{d\phi^2}{d\theta^2} \cdot dy_1^2 + r^2 \cdot \sin^2\theta \cdot \sin^2\phi \cdot \frac{d\eta^2}{d\theta^2} \cdot dz_1^2 - \color{orange}{dr^2} =} \quad \rightarrow (1) $


Переходные коэффициенты при этом равны:

$dx_1^2 = d\theta^2; \\ dy_1^2 = \sin^2 \theta \cdot d\phi^2 = \sin^2 \theta \cdot \frac{d\phi^2}{d\theta^2} \cdot d\theta^2 = \sin^2 \theta \cdot \left( \frac{d\phi}{d\vec{r}} \cdot \frac{d\vec{r}}{d\theta} \right)^2 \cdot d\theta^2 = \\ = \sin^2\theta \cdot \left( \frac{g_\theta}{g_\phi} \right)^2 \cdot d\theta^2 = \frac{\sin^2\theta}{\sin^2\theta} \cdot d\theta^2 = d\theta^2; \\ \frac{d\eta^2}{d\theta^2} = \frac{g_\theta^2}{g_\eta^2} = \frac{1}{\sin^2\theta \cdot \sin^2\phi };$


Поэтому с учётом базисных векторов:

$(1) \rightarrow \quad \color{green}{= r^2 \cdot dx_1^2 \cdot \vec{e_{\theta}}^2 + r^2 \cdot dy_1^2 \cdot \vec{e_{\phi}}^2 + r^2 \cdot dz_1^2 \cdot \vec{e_{\eta}}^2 - \color{orange}{dr^2 \cdot \vec{e_r}^2} = } \quad \rightarrow \ (2)$


что представляет 3-пространство $\psi'_1(x_1, y_1, z_1)$ с линейными по $d\theta$ базисными векторами, масштабным фактором $r$ и мгновенной длиной $dl^2 = dx_1^2 + dy_1^2 + dz_1^2$, в нашем случае совокупно редуцированной на величину $dr^2/r^2$:

$(2) \rightarrow \quad \color{green}{ = r^2 \cdot \left( dx_1^2 \cdot \vec{e_\theta}^2 + dy_1^2 \cdot \vec{e_\phi}^2 + dz_1^2 \cdot \vec{e_\eta}^2 - \color{orange}{\frac{dr^2}{r^2} \cdot \vec{e_r}^2} \right) = } \quad \rightarrow \ (3)$


Без оранжевой составляющей получилась пространственная часть интервала стандартной космологической модели для «плоского» пространства с возможной деградацией пространственного масштабного фактора $r$ по времени, как в FLRW.

Гиперповерхность 3-сферы является внутри себя линейной по угловым координатам, или, иначе говоря, пространственная часть интервала получилась «плоской» для неизменного $r \ (dr = 0)$. «Упаковать» лишний $dr^2$ будет практичнее снова в сферических, только уже обычных для трёхмерной сферы $(x_1, y_1, z_1) \rightarrow(\rho, \varphi, \zeta)$. Чтобы различать координаты для 3-сферической и 2-сферической систем, последние обозначим $(\rho, \varphi, \zeta)$:

$(3) \rightarrow \quad \color{green}{ r^2 \cdot \left( dx_1^2 + dy_1^2 +dz_1^2 - \color{orange}{\frac{dr^2}{r^2}} \right) = r^2 \cdot \left( d\rho^2 - \color{orange}{\frac{dr^2}{r^2}} + \rho^2 \cdot d\varphi^2 + \rho^2 \cdot \sin^2 \varphi \cdot d\zeta^2 \right) = \\ = r^2 \cdot \left( \left(1 - \color{orange}{\frac{d(\ln r)^2}{d\rho^2}} \right) d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right) }$


где порядок отношения величин $ dr = r d\rho \ \Rightarrow r = e^\rho $, а $\varphi, \zeta$ по теореме тангенсов:

${ d\varphi = \frac{r}{\rho} \cdot d\phi; \\ d\zeta = \frac{r \cdot \sin \phi}{\rho \cdot \sin\varphi} \cdot d\eta. }$


Тогда полный интервал будет:

$ds^2 = \color{red}{(-1)\cdot dt^2 \left( 1 - \color{magenta}{\frac{dr^2}{dt^2}} \right)} + \color{green}{ r^2 \cdot \left( \left(1 - \color{orange}{\frac{d(\ln r)^2}{d\rho^2}} \right) d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right)} \qquad (A)$


Получился комбинированный интервал словно «слепленный» из вида интервала метрики FLRW и метрики Шварцшильда, каждый из которых представляет частный случай физических взаимодействий. Теперь посмотрим как из $(A)$ получаются соответствующие решения.

Вид интервала для метрики Фридмана


Чисто математически интервал вида $(A)$ превращается в метрику FLRW стандартной космологической модели простым исключением энергетической составляющей $dr = 0$:

$ds^2 = \color{red}{(-1)\cdot dt^2} + \color{green}{ r^2 \cdot \left( d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2) \right)}$


Что, как показано выше, можно также переписать так:

$ds^2 = \color{red}{(-1)\cdot dt^2} + \color{green}{ r^2 \cdot \left( dx^2 + dy^2 + dz^2 \right)}$


Решение уравнений ОТО для такого интервала даёт зависимость $r \propto t^{2/3}$.

Однако, эмпирические данные ККС для объектов $z>0.3$ показывают консолидированное отклонение от этой зависимости.

Возможно, решение для интервала вида $(A)$ даст более точную зависимость, но я пока его не нашёл.

Решение ОТО через метрику Шварцшильда


Сравним полученный интервал с метрикой Шварцшильда:

$ds^2 = -\color{red}{(1-\frac{\rho_s}{\rho})} \cdot dt^2 + \color{orange}{\frac{1}{1 - \frac{\rho_s}{\rho}}} \cdot d\rho^2 + \rho^2 \cdot d\phi^2 + \rho^2 \sin^2 \phi \cdot d\zeta^2$


Если представить систему взаимодействующих объектов в низкоэнергетическом масштабе $(dr/r \rightarrow \infty)$, то $r$ можно принять равным единице без потери математической связности, пространство при этом станет псевдоевклидовым, а интервал $(A)$ можно переписать следующим образом:

$ds^2 = (-1)\cdot \color{red}{ \left( 1 - \frac{dr^2}{dt^2} \right) } \cdot dt^2 + \color{orange}{ \left(1 - \frac{dr^2}{d\rho^2} \right) } \cdot d\rho^2 + \rho^2 \cdot ( d\varphi^2 + \sin^2 \varphi \cdot d\zeta^2)$


Математически это ровно то же самое, как если бы мы выполнили фокус $\pm dr^2$ для пустого 3-пространства в сферических координатах $(\rho, \varphi, \zeta)$.

То есть для плоского вакуумного случая интервал $(A)$ будет иметь решение аналогичное решению метрики Шварцшильда, при условии эквивалентности подцвеченных красным и оранжевым множителей. Получим систему:

$1-\frac{\rho_s}{\rho} = 1 - \frac{dr^2}{dt^2}; \\ \frac{1}{1 - \frac{\rho_s}{\rho}} = 1 - \frac{dr^2}{d\rho^2}.$


где $t, r, \rho $ — по порядку: время, кривизна (энергия), радиус (расстояние) в сферически симметричном гравитационном поле по нулевой общей кривизне пространства.
Путём нехитрых математических преобразований получим весьма лаконичное решение:

$-dt^2 + dr^2 - d\rho^2 = 0, $


которое подтверждает, что:

  1. Четвёртая координата линейна радиальной координате.
  2. Четвёртая координата является координатой по мнимой оси.

Первое, на мой взгляд, очень важно, потому что показывает, что энергия, представленная как дополнительная ось, почти изотропна наблюдаемым. Второе — позволяет понять, почему она проявляет себя иначе. И «ненаблюдаема».

Кроме того, хочется отметить, что сама постановка в интервале энергии с отрицательным знаком относительно пространства и положительным относительно времени позволяет сформулировать их взаимоотношения следующим образом: пространство — это энергия-время, оно преодолевается за энергию-время.

Резюме


Мне кажется, продолжение курса на геометризацию физики показывает себя весьма перспективным направлением. Мнимость энергетической оси в космологии могла бы послужить перекидным мостиком к уравнениям Максвелла.
Заметки на полях. Забегая вперёд, позволю себе предположить, что одного мнимого измерения для организации механизмов заряда и массы будет мало. Плюс электро-магнитный дуализм как аргумент в пользу не менее двух измерений. И некоторая симметрия в форме: временное измерение + два энергетических = три пространственных.
При переходе к микро масштабам я попробую двигаться в направлении «расщепления» $r$:

$ds^2 = - dt^2 - dv^2 - dw^2 + dx^2 + dy^2 + dz^2$




Ремарка 23.08.2020:


Мнимость дополнительной оси $r$ была изначально задана знаком, с которым $\pm dr^2$ были разнесены под темпоральную и пространственную составляющие. То есть, если представить гравитационное поле не воронкой, а холмом, то четвёртое измерение получится сонаправленным пространству:

$dt^2 + dr^2 + d\rho^2 = 0 $


Подобная индифферентность проявляемых в (1,3) свойств от направления пятой оси, по-видимому, является признаком её замкнутой формы.