Предисловие
(из статьи КОМПЬЮТЕРНАЯ СТЕГАНОГРАФИЯ ВЧЕРА, СЕГОДНЯ, ЗАВТРА. Технологии информационной безопасности 21 века. /Барсуков В. С., к.т.н., Романцов А.П./1998/)
Задача надежной защиты информации от несанкционированного доступа является одной из древнейших и не решенных до настоящего времени проблем. Способы и методы скрытия секретных сообщений известны с давних времен, причем, данная сфера человеческой деятельности получила название стеганография. Это слово происходит от греческих слов steganos (секрет, тайна) и graphy (запись) и, таким образом, означает буквально “тайнопись”, хотя методы стеганографии появились, вероятно, раньше, чем появилась сама письменность (первоначально использовались условные знаки и обозначения).
В дальнейшем для защиты информации стали использоваться более эффективные на время создания методы кодирования и криптографии.
Как известно, цель криптографии состоит в блокировании несанкционированного доступа к информации путем шифрования содержания секретных сообщений. Стеганография имеет другую задачу, и ее цель — скрыть сам факт существования секретного сообщения. При этом, оба способа могут быть объединены и использованы для повышения эффективности защиты информации (например, для передачи криптографических ключей).
Как и любые инструменты, стеганографические методы требуют к себе внимания и осторожного обращения, так как могут быть использованы как для целей защиты, так и для целей нападения.
Алгоритм
В соответствии с методом широкополосного сигнала, каждый бит данных кодируется последовательностью изменённых яркостей пикселей в соответствии со значениями бит псевдослучайной последовательности.
Метод широкополосного сигнала предполагает возможность выработки у отправляемой и принимающих сторон одинаковой псевдослучайной последовательности или, по крайней мере, псевдослучайных последовательностей со статистическими характеристиками эквивалентными равным.
При этом в качестве контейнера для размещения данных может выступать не только само изображение, но и обратимое преобразование этого изображения, например, спектр, получаемый в результате Фурье преобразований. Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов не очень сложной задачей для программирования.
Формула размещения данных в графическом файле
Формула изменения яркостей пикселей в зависимости от значения i-го бита данных x[i] и j-го бита псевдослучайной последовательности y[j]:
Cw[i,j] = C[i,j] + A*(-1)^(x[i] xor y[j])
где
C[i,j] — значение яркости пикселя графического изображения сопоставленного i-му биту данных x[i] и j-му биту псевдослучайной последовательности y[j]
A — значение изменения яркости (параметр метода — глубина погружения)
Формула извлечения данных из графического файла
При извлечении данных из массива яркостей пикселей применяется взвешенная схема голосования с коэффициентами равными разности между средним значением яркости и яркостью голосующего пикселя.
V[i]= SUM (Cw[i,j]-Mw[i,j])(-1)^y[j]
if V[i]<0 then x[i] == 0 else x[i] == 1
где
Cw[i,j] — значение яркости пикселя декодируемого графического изображения сопоставленного i-му биту данных x[i] и j-му биту псевдослучайной последовательности y[j]
Mw[i,j] — значение средней яркости пикселей вокруг пикселя декодируемого графического изображения сопоставленного i-му биту данных x[i] и j-му биту псевдослучайной последовательности y[j]
Компенсация изменения средней яркости изображения при применении метода широкополосного сигнала
Использование псевдослучайной последовательности с характеристиками приближенными к равновероятной, для кодирования данных, позволяет сохранить среднюю яркость пикселей у исходного графического изображения и у изображения, содержащего внедрённые данные.
Однако при прямом и дословном применении алгоритма средняя яркость пикселей могла бы иметь смещение относительно средней яркости у исходного изображения.
Для оценки величины смещения производится статистический подсчёт числа нулей и единиц у функции (x[i] xor y[j])
И если p0 — вероятность нулей, а p1 — вероятность единиц, то оценка величины изменения средней яркости вычисляется по формуле:
dC = A*(p0-p1)
Данную оценку dC будем использовать в формуле самого алгоритма метода широкополосных сигналов для компенсации смещения средней яркости изображения
Cw[i,j] = C[i,j] + A*(-1)^(x[i] xor y[j]) — dC
Использование изображения с подавлением шумов
Поскольку изменение яркостей в большую или меньшую сторону носит равновероятный характер (или по крайней мере это предполагается методикой), то усреднённая яркость исходного изображения должна практически совпадать с усреднённой яркостью у сформированного применением метода изображения. Это же правило, видимо, должно выполнятся и для небольших участков изображения.
Таким образом можно предполагать, что практически должны совпадать изображения полученные в результате устранения шумов из исходного изображения и в результате устранения шумов из сформированного изображения, а значит изображение, полученное применением фильтра устранения шумов может быть выбрано в качестве известной отправителю и получателю информации.
Таким образом формула размещения данных в графическом файле может быть заменена на формулу
Cw[i,j] = M[i,j] + A*(-1)^(x[i] xor y[j])
где
M[i,j] — значение средней яркости пикселей вокруг пикселя кодируемого графического изображения сопоставленного i-му биту данных x[i] и j-му биту псевдослучайной последовательности y[j]
Автоматическое вычисление глубины погружения.
При использовании для размещения данных в графическом файле формулы
Cw[i,j] = С[i,j] + A*(-1)^(x[i] xor y[j]) — dC
а для извлечения данных из графического файла формулы
V[i]= SUM (Cw[i,j]-Mw[i,j])(-1)^y[j]
if V[i]<0 then x[i] == 0 else x[i] == 1
можно дать оценку для выбора оптимального значения параметра алгоритма — величины погружения A исходя из статистических оценок.
Так добавление или вычитание значения A из значений яркости пикселей увеличит квадрат дисперсии итогового изображения на величину A^2.
При этом полагаем равновероятным добавление и вычитание значения A из яркости пикселя.
А значит, при использовании в формуле восстановления локально усреднённой величины M, можно задать значение A по следующей формуле
A = SQRT( AVG (C[i,j]-M[i,j])^2 )
Роль коэффициентов в схеме голосования
При использовании в оригинальной методике схемы голосования, коэффициенты голосов, равные разности между средним значением яркости и яркостью голосующего пикселя, являются коэффициентами голосов из статистического критерия разделения двух простых статистических гипотез известного под названием «Наиболее мощный» для разделения двух простых гипотез о нормальном распределении либо с параметрами (A,A), либо с параметрами (-A,A).
Поскольку, при получении и извлечении данных из графического файла достоверно не известна величина A, то в качестве среднего может быть выбрана её оценка, равная SQRT( AVG (Cw[i,j]-Mw[i,j])^2 ), которая в свою очередь, совпадает и с дисперсией этого же распределения.
Доказательство
Коэффициенты голосов, при использовании статистического критерия «Наиболее мощный», могут быть вычислены по формуле -log(P1(x)/P0(x)), где P0 и P1 — значение вероятности у исследуемых статистик, а величина x является значением разности между средним значением яркости и яркостью голосующего пикселя.
Pn(x) = exp(-(x-A)^2/A^2)/(SQRT(2*pi)*A)
-log(Pn(x)) = -log(exp(-(x-A)^2/A^2)/(SQRT(2*pi)*A)) = (x-A)^2/A^2+log(SQRT(2*pi)*A),
а значит
-log(Pn(x)/Pn(-x))=(x-A)^2/A^2+log(SQRT(2*pi)*A)-(-x-A)^2/A^2-log(SQRT(2*pi)*A)=((x-A)^2-(x+A)^2)/A^2 = 4*x/A^2 = O(x)
Таким образом использование схемы голосования с коэффициентами голосов равными разности между средним значением яркости и яркостью голосующего пикселя является статистического критерием разделения двух простых статистических гипотез известного под названием «Наиболее мощный» для разделения двух простых гипотез о нормальном распределении с параметрами (A,A) и с параметрами (-A,A).
Улучшение схемы голосования
Будем продолжать использовать статистической критерий разделения двух простых статистических гипотез известного под названием «Наиболее мощный», однако для расчёта вероятностей используем не предопределённую гипотезу о нормальном распределении разности между средним значеним яркости и яркостью голосующего пикселя, а фактическую выборочную статистическую информацию из имеющихся в наличии данных.
Пусть
Pw(x) — выборочное распределение фактически вычисленных значений Cw[i,j]-Mw[i,j], где Cw[i,j] — значение яркости пикселя декодируемого графического изображения и Mw[i,j] — значение средней яркости пикселей вокруг пикселя декодируемого графического изображения сопоставленные i-му биту декодируемых данных x[i] и j-му биту псевдослучайной последовательности y[j].
dCw = A*(p0-p1) = E Pw = SUM i*Pw(i) = AVG (Cw[i,j]-Mw[i,j]) — выборочная средняя значение смещения яркости у размытого изображения
Aw = SQRT(E Pw^2 — (E Pw)^2) = SQRT(SUM i^2*Pw(i) — (SUM i*Pw(i))^2) — выборочная дисперсия значение смещения яркости у размытого изображения
Способ 1
Используем поправочный коэффициент dCw при подсчёте голосов
V[i]= SUM (Cw[i,j]-Mw[i,j]-dCw)(-1)^y[j]
Способ 2
Будем применять статистический критерий «Наиболее мощный» для разделения двух гипотез со средними значениями выше и ниже величины dCw и функциями распределения P1 и P2, такими, что P1(dCw+x)=P0(dCw-x) и P1xP0=Pw -где P1xP0(t)= SUM P1(i)*P0(j)|i+j=t — операция свёртки двух функций.
Полагая P1(dCw+x)=P0(dCw-x)=f(x), восстановим неизвестное распределение f(x) из её функции собственной свёртки fxf,
Полагаем что для известного вычисленного выборочного распределения Pw(x), выполняется равенство fxf(x)=Pw(dCw+x)
После того как будет вычислена функция f(x), будем использовать для голосования коэффициенты голосов вычисляемые по формуле -log(f(x-dCw)/f(x+dCw))
Формулы, реализованные в библиотеке
Формула размещения данных в графическом файле
Формула изменения яркостей пикселей в зависимости от значения i-го бита данных x[i] и j-го бита псевдослучайной последовательности y[j]:
Cw[i,j] = C[i,j] + A*(-1)^(x[i] xor y[j])
где
C[i,j] — значение яркости пикселя графического изображения сопоставленного i-му биту данных x[i] и j-му биту псевдослучайной последовательности y[j]
A = SQRT( AVG (C[i,j]-M[i,j])^2 )
Формула извлечения данных из графического файла
При извлечении данных из массива яркостей пикселей применяется взвешенная схема голосования с коэффициентами равными разности между средним значением яркости и яркостью голосующего пикселя.
V[i]= SUM (log(Pn(Cw[i,j]-Mw[i,j])/Pn(Mw[i,j]-Cw[i,j]))(-1)^y[j]
if V[i]<0 then x[i] == 0 else x[i] == 1
где
Pn — значение вероятности у статистики с нормальным распределением, средним значением и значением дисперсии равным A=SQRT( AVG (Cw[i,j]-Mw[i,j])^2 )
Cw[i,j] — значение яркости пикселя декодируемого графического изображения сопоставленного i-му биту данных x[i] и j-му биту псевдослучайной последовательности y[j]
Mw[i,j] — значение средней яркости пикселей вокруг пикселя декодируемого графического изображения сопоставленного i-му биту данных x[i] и j-му биту псевдослучайной последовательности y[j]
Требуемый размер изображения
Если
— L8 — количество бит передаваемых данных
— N — количество изменяемых пикселей на каждый переданный бит
то требуемое количество пикселей в графическом изображении должно быть не менее L8*N, то есть должно выполняться неравенство L8*N >= W*H*K, где W и H — ширина и высота графического изображения, K — количество цветовых каналов у графического изображения.
Реализация метода широкополосного сигнала
— Для выработки псевдослучайной последовательности и для выработки индексов позиций для внедрения бит данных в изображение используются алгоритмы с использованием данных, задаваемых пользователем, и называемых стеганографическим ключом.
— Хотя для выработки псевдослучайной последовательности и для выработки индексов используются криптографические алгоритмы, как алгоритмы с наиболее изученными статистическими свойствами, метод широкополосного сигнала НЕ ЯВЛЯЕТСЯ ШИФРОВАНИЕМ, а является одним из методов скрытной передачи информации, то есть СТЕГАНОГРАФИЧЕСКИМ методом.
— Значения средней яркости пикселей получены применением графического фильтра размытия к поступившему графическому изображению.
Дополнительные опции в текущей реализации библиотеки
В дополнение к самому методу широкополосного сигнала в текущей реализации библиотеки встроенны алгоритмы, с помощью которых
— исходный образец графического изображения может быть автоматически масштабирован до размера достаточного для передачи всех необходимых данных
— требуемая глубина погружения может вычисляется автоматически
— исходные данные являются текстов формата RTF и могут быть сжаты алгоритмом компрессии данных,
— к передаваемым данным могут быть добавлены коды исправления ошибок,
— последовательности бит могут размещаться в изображении не последовательно, а в соответствии с выбранным алгоритмом размещения бит в графическом файле.
— параметры алгоритмов программы могут быть внедрены в передаваемое изображение в виде баркода. Для выработки псевдослучайной последовательности и для выработки индексов для внедрения бит данных в изображение используются алгоритмы с использованием строки, вводимой пользователем, и называемой стеганографическим ключом. При передаче данных стеганографический ключ передаётся вместе с баркодом.
Используемое программное обеспечение
— Microsoft Visual Studio 2013 C# — среда и язык программирования
— EmguCV/OpenCV – C#/C++ библиотека структур и алгоритмов для обработки изображений
— FFTWSharp/FFTW – C#/C++ библиотека реализующая алгоритмы быстрого дискретного преобразования Фурье
— ZXing.Net — .Net библиотека для обработки баркодов
— FFTTools — C# библиотека, реализующая алгоритмы использования БФП для цифровой обработки изображений github.com/dprotopopov/FFTTools
Скриншоты программ
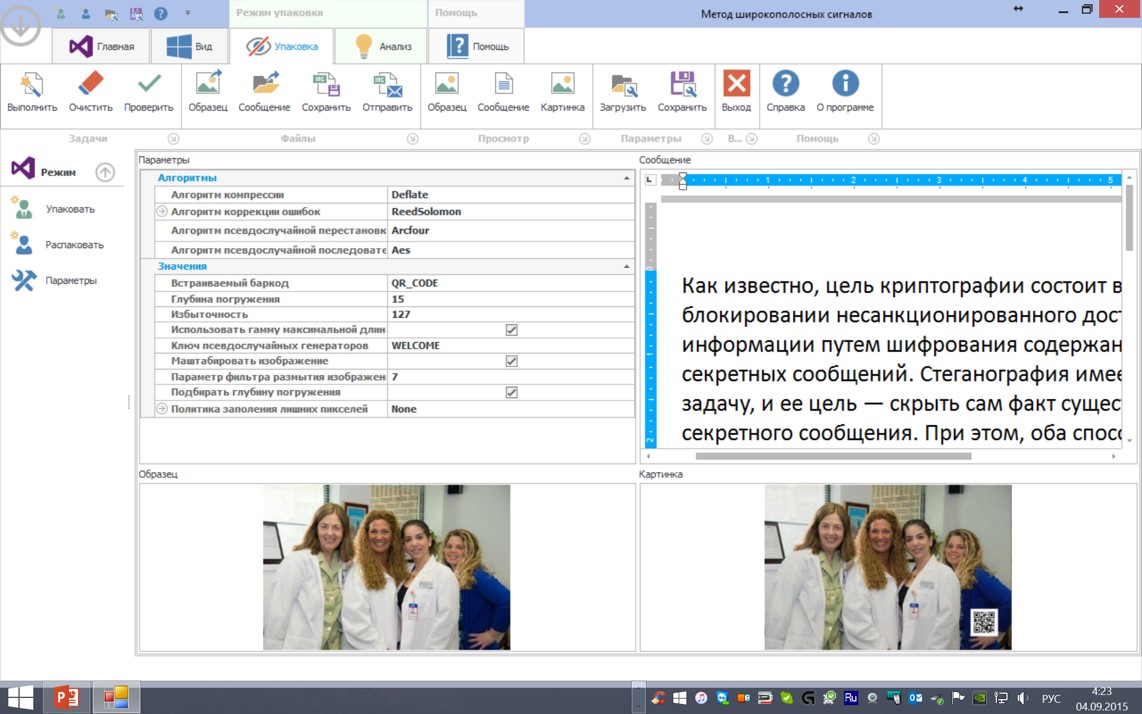
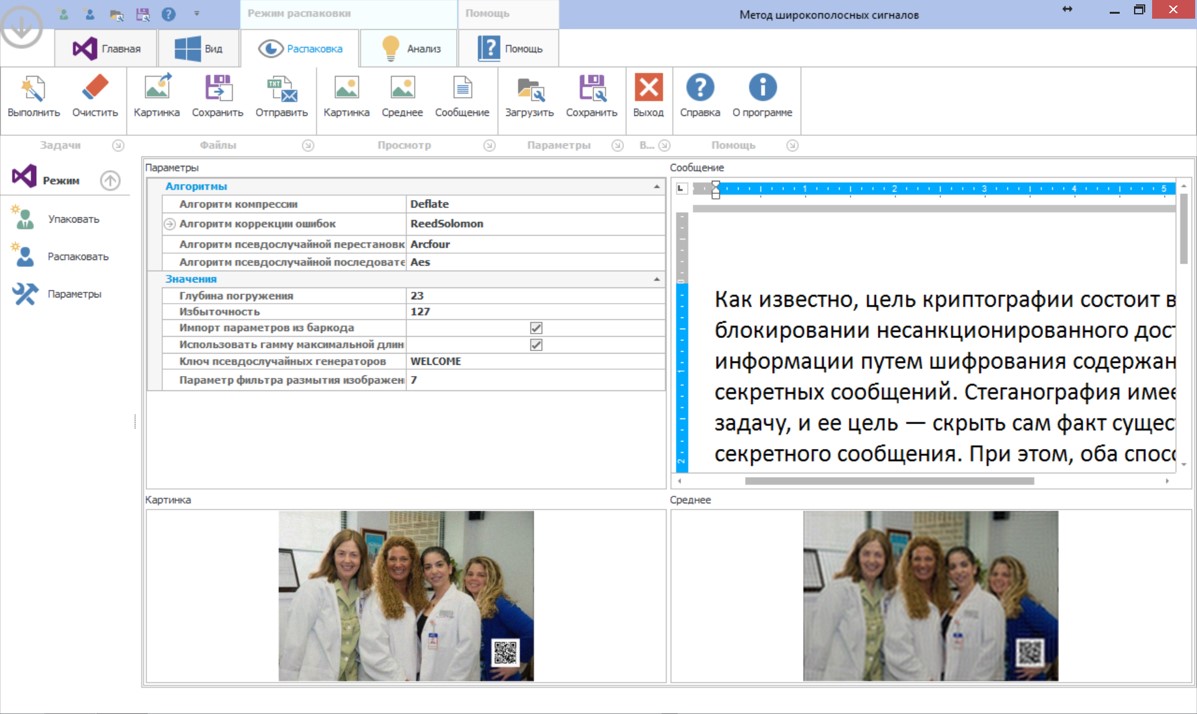
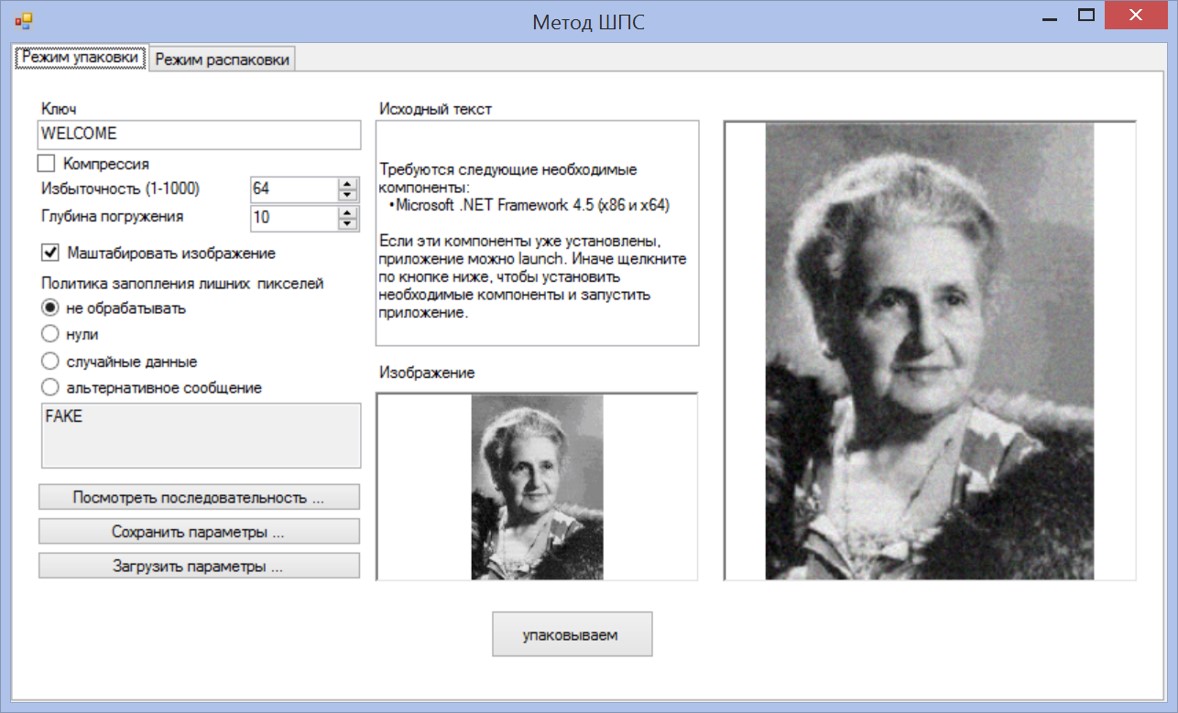
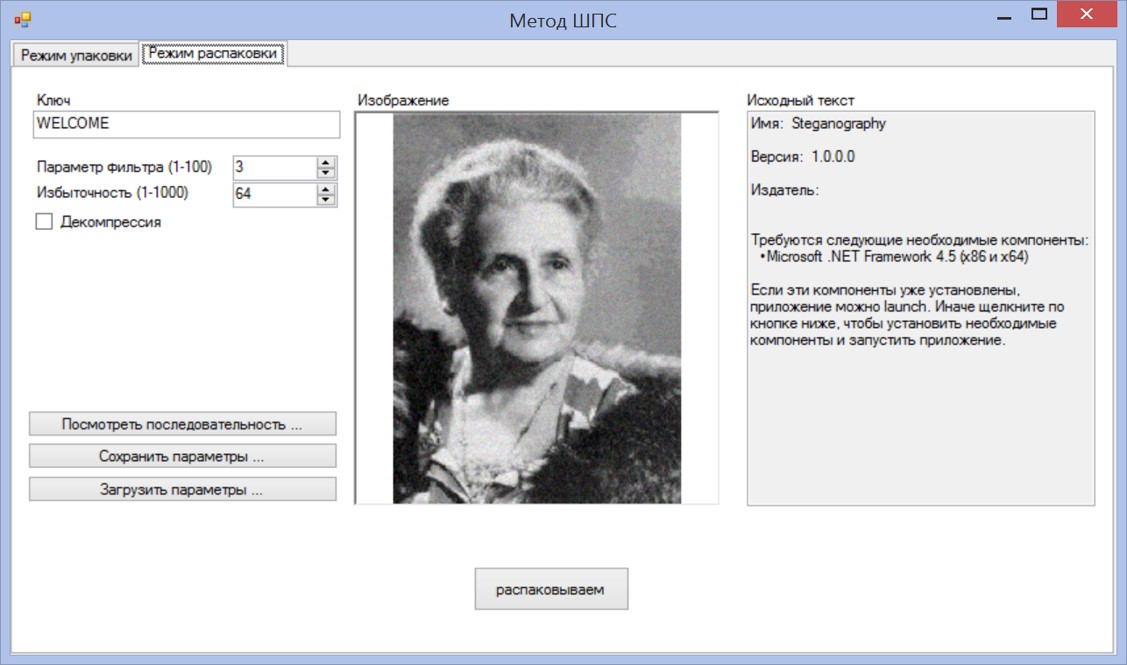
Литература
— Барсуков Вячеслав Сергеевич, кандидат технических наук. Романцов Андрей Петрович. КОМПЬЮТЕРНАЯ СТЕГАНОГРАФИЯ ВЧЕРА, СЕГОДНЯ, ЗАВТРА. Технологии информационной безопасности 21 века. Публикация. 1998. www.ess.ru/sites/default/files/files/articles/1998/0405/1998_0405_03.pdf
— Дмитрий Протопопов. Фурье-обработка цифровых изображений. Интернет-публикация. habrahabr.ru/post/265781
Интернет-адрес проекта: github.com/dprotopopov/mssove2

