В задачах интерполяции функций по заданным значениям функции для заданного набора аргументов широко применяется формула аппроксимации функции полиномом, совпадающего в заданных точках со значениями исследуемой функции.

Такой вид аппроксимации широко используется в научных расчетах.

Пример: некоторую функцию очень дорого вычислять для каждого значения аргументов (а их много, допустим N) — поэтому строится таблица значений и при необходимости получения значения функции в определенной точке — интерполируется по табличке. Разумеется, изначальное построение таблицы и процедура интерполирования (N раз) должны быть «дешевле», чем точное вычисление самой функции N раз.

Обобщим эту формулу на случай функции нескольких переменных

Скалярное произведение векторов будем вычислять с учётом квадратов дисперсий значений аргументов Dx

• с целью учета равнозначности каждой координаты аргумента вычисляем Dx[k] =M2[k] ? M1[k]?M1[k]
• < A; B > = SUM A[k] * B[k] / Dx[k]

Алгоритм

1. Для заданных векторов Xi рассчитываем вектор Dx квадратов дисперсий значений аргументов
2. Для вектора X находим p ближайших точек X1,...,Xp, где расстояния между точками вычисляется с учётом квадратов дисперсий значений аргументов
3. Вычисляем значение полинома P(X) = SUM Yi*П < X-Xj, Xi-Xj > / < Xi-Xj, Xi-Xj >, где скалярное произведение вычисляется с учётом квадратов дисперсий значений аргументов

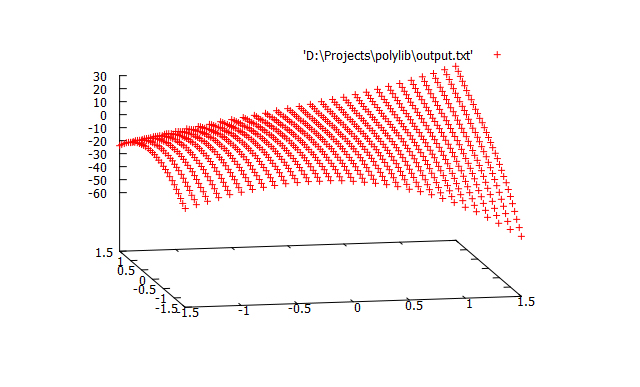
Демонстрация аппроксимации для функции двух переменных

history.txt

• -1 -1 -10
• 1 1 10
• 0 0 0
• -1 1 -8
• 1 -1 -20

Построим график значений полинома на решётке с шагом 0.1 в программе gnuplot

• predict.exe -history history.txt -input input.txt -output output.txt -p 5
• splot «output.txt»

// predict.cpp: определяет точку входа для консольного приложения.
//

#include "stdafx.h"

struct t_previous_result
{
	std::vector<double> x;
	double y;
};

/////////////////////////////////////////////////////////
// Вычисление квадрата растояния между двумя векторами координат
double delta(std::vector<double>& a, std::vector<double>& b, std::vector<double>& dx)
{
	auto s = 0.0;
	auto i = 0;
	for (; i < a.size() && i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += (a[i] - b[i]) * (a[i] - b[i]) / dx[i];
	for (; i < a.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += a[i] * a[i] / dx[i];
	for (; i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += b[i] * b[i] / dx[i];
	return s;
}

/////////////////////////////////////////////////////////
// Вычисление растояния проекции двух векторов
double scalar(std::vector<double>& a, std::vector<double>& b, std::vector<double>& dx)
{
	auto s = 0.0;
	auto i = 0;
	for (; i < a.size() && i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += (a[i] * b[i]) / dx[i];
	return s;
}

/////////////////////////////////////////////////////////
// Возвращает предсказание для указанных параметров исходя из исторических данных
double predict(std::vector<double>& x,
               std::vector<t_previous_result>& previous_results,
               std::vector<double>& dx,
               int p)
{
	std::vector<std::pair<t_previous_result, double>> neighbors;
	for (auto it = previous_results.begin(); it != previous_results.end(); ++it)
	{
		std::vector<double>& x2 = it->x;
		auto d = delta(x, x2, dx);
		std::pair<t_previous_result, double> pair(*it, d);
		neighbors.push_back(pair);
	}
	std::sort(neighbors.begin(), neighbors.end(),
	          [](std::pair<t_previous_result, double> const& a, std::pair<t_previous_result, double> const& b)
	          {
		          return (a.second < b.second);
	          });
	neighbors.resize(std::min(p, static_cast<int>(neighbors.size())));
	auto y = 0.0;
	for (auto iti = neighbors.begin(); iti != neighbors.end(); ++iti)
	{
		auto s = iti->first.y;
		std::vector<double>& xi = iti->first.x;
		for (auto itj = neighbors.begin(); itj != neighbors.end(); ++itj)
		{
			if (iti == itj) continue;
			std::vector<double>& xj = itj->first.x;
			std::vector<double> xxj;
			std::vector<double> xixj;
			for (auto i = 0; i < x.size() && i < xj.size(); i++) xxj.push_back(x[i] - xj[i]);
			for (auto i = 0; i < xi.size() && i < xj.size(); i++) xixj.push_back(xi[i] - xj[i]);
			s *= scalar(xxj, xixj, dx) / scalar(xixj, xixj, dx);
		}
		y += s;
	}
	return y;
}

/////////////////////////////////////////////////////////
// Дефолтные значения
static const int _p = 3;

int main(int argc, char* argv[])
{
	std::vector<t_previous_result> previous_results;
	std::vector<double> dx;
	char* input_file_name = nullptr;
	char* output_file_name = nullptr;
	char* previous_results_file_name = nullptr;
	auto p = _p;
	std::string line;

	// Поддержка кириллицы в консоли Windows
	// Функция setlocale() имеет два параметра, первый параметр - тип категории локали, в нашем случае LC_TYPE - набор символов, второй параметр — значение локали. 
	// Вместо второго аргумента можно писать "Russian", или оставлять пустые двойные кавычки, тогда набор символов будет такой же как и в ОС.
	setlocale(LC_ALL, "");

	for (auto i = 1; i < argc; i++)
	{
		if (strcmp(argv[i], "-help") == 0)
		{
			std::cout << "Usage :\t" << argv[0] << " [-input <inputfile>] [-output <outputfile>] [...]" << std::endl;
		}
		else if (strcmp(argv[i], "-input") == 0) input_file_name = argv[++i];
		else if (strcmp(argv[i], "-output") == 0) output_file_name = argv[++i];
		else if (strcmp(argv[i], "-history") == 0) previous_results_file_name = argv[++i];
		else if (strcmp(argv[i], "-p") == 0) p = atoi(argv[++i]);
	}

	if (input_file_name != nullptr) freopen(input_file_name, "r", stdin);
	if (output_file_name != nullptr) freopen(output_file_name, "w", stdout);
	if (previous_results_file_name != nullptr)
	{
		std::vector<double> m1;
		std::vector<double> m2;
		std::ifstream history(previous_results_file_name);
		if (!history.is_open()) throw "Error opening file";
		while (std::getline(history, line))
		{
			std::stringstream ss(line);
			std::vector<double> x;
			std::copy(std::istream_iterator<double>(ss), std::istream_iterator<double>(),
				std::back_inserter(x));
			auto y = x.back();
			x.pop_back();
			t_previous_result previous_result;
			previous_result.x = x;
			previous_result.y = y;
			previous_results.push_back(previous_result);
			for (auto i = 0; i < x.size(); i++)
			{
				if (i >= m1.size()) m1.push_back(0.0);
				if (i >= m2.size()) m2.push_back(0.0);
				m1[i] += x[i];
				m2[i] += x[i] * x[i];
			}
		}
		for (auto it = m1.begin(); it != m1.end(); ++it) *it /= previous_results.size();
		for (auto it = m2.begin(); it != m2.end(); ++it) *it /= previous_results.size();
		for (auto i = 0; i < m1.size() && i < m2.size(); i++) dx.push_back(m2[i] - m1[i] * m1[i]);
	}
	while (std::getline(std::cin, line))
	{
		double y;
		std::vector<double> x;
		std::stringstream ss(line);
		std::copy(std::istream_iterator<double>(ss), std::istream_iterator<double>(),
			std::back_inserter(x));
		y = predict(x, previous_results, dx, p);
		for (auto it = x.begin(); it != x.end(); ++it) std::cout << *it << ' ';
		std::cout << y << std::endl;
	}
	return 0;
}

Интернет-адрес проекта: https://github.com/dprotopopov/polylib

Используемое программное обеспечение

• Microsoft Visual Studio 2013 — среда программирования
• gnuplot — кросс-платформенный инструмент для построения графиков www.gnuplot.info