Как правило, для вычисления расстояний между изображениями используется формула, являющаяся суммой модулей или квадратов разностей интенсивности:
d(X,Y) = SUM ( X[i,j] — Y[i,j] )^2
Если помимо простого сравнения двух изображений требуется решить задачу обнаружения позиции фрагмента одного изображения в другом, то классический метод “начального уровня”, заключающийся в переборе всех координат и вычисления расстояния по указанной формуле, как правило, терпит неудачу практического использования из-за требуемого большого количества вычислений.
Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований для расчёта меры совпадения двух изображений при различных смещениях их между собой. Вычисления при этом происходят одновременно для различных комбинаций сдвигов изображений относительно друг друга.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов сравнения изображений не очень сложной задачей для программирования.
Постановка задачи
- Пусть даны два изображения X и Y – изображение и образец, размеров (N1,N2) и (M1,M2) соответственно и Ni > Mi
- Требуется найти координаты образца Y в полном изображении X и вычислить оценочную величину — меру близости.
Например, найти:
образец

в изображении

Корреляция как мера между изображениями
Согласно определению, корреляцией <F,G> двух функций F и G называется величина:
<F,G> = SUM F(i)*G(i)
Эта величина хорошо известна из курса математики и геометрии, посвященного линейным пространствам, где носит название скалярного произведения. Будем использовать в качестве меры между изображениями формулу:
m(X,Y) = SUM ( X[i,j] * Y[i,j] ) / ( SQRT ( SUM X[i,j] ^2 ) * SQRT ( SUM Y[i,j] ^2 ) )
или
m(X,Y) = <X,Y> / ( SQRT (<X,X> ) * SQRT (<Y,Y> ) )
Данная величина получена из операции скалярного произведения векторов (рассматривая изображения как векторы в многомерном пространстве). И даже более — эта же формула представляет собой и стандартную статистическую формулу критерия для гипотезы о совпадении двух вероятностных распределений.
Примечание:
При вычислении корреляции между фрагментами изображений, если одно изображение меньше другого, будем делить только на значение норм у пересекающийся частей.
Свёртка двух функций
Согласно определению, свёрткой двух функций F и G называется функция FхG:
FхG(t) = SUM F(i)*G(j)|i+j=t
Пусть G’(t) = G(-t) и F’(t) = F(-t), тогда, очевидна справедливость равенств:
- FхF’(0) = SUM F(i)^2 – скалярное произведение вектора F на самого себя
- GхG’(0) = SUM G(j)^2– скалярное произведение вектора G на самого себя
- FхG’(0) = SUM F(i)*G(i) – скалярное произведение двух векторов F и G
Так же очевидно, что FхG’(t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t (это легко проверить явной подстановкой значений в формулу корреляции).
Преобразование Фурье
Преобразование Фурье (?) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:
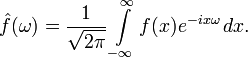
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «?» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.
Кроме того, существуют разнообразные обобщения данного понятия.
Многомерное преобразование Фурье
Преобразование Фурье функций, заданных на пространстве ?^n, определяется формулой:
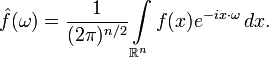
Обратное преобразование в этом случае задается формулой:
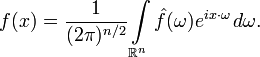
Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.
Дискретное преобразование Фурье
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Формулы дискретных преобразований
Прямое преобразование:
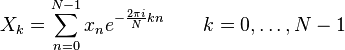
Обратное преобразование:
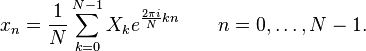
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:
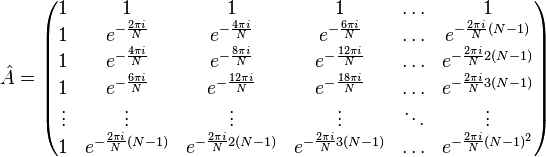
Фурье-преобразования для вычисления свёртки
Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).
И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула
FхG = BFT ( FFT(F)*FFT(G) )
Где
- FFT – операция прямого преобразования Фурье
- BFT – операция обратного преобразования Фурье
Проверить правильность равенства довольно легко – явно подставив в формулы Фурье-преобразований и сократив получившиеся формулы
Фурье-преобразования для вычисления корреляции
Пусть <F,G>(t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t
Тогда, как уже показано ранее, выполняется
<F,G>(t) = FхG’(t) = BFT ( FFT(F)*FFT(G’) )
Если используются реализации алгоритма трансформации Фурье через комплексные числа, то такие преобразования обладают ещё одним замечательным свойством:
FFT(G’) = CONJUGATE ( FFT(G) )
Где CONJUGATE ( FFT(G) ) – матрица, составленная из сопряжённых элементов матрицы FFT(G)
Таким образом, получаем
<F,G>(t) = BFT ( FFT(F)*CONJUGATE ( FFT(G) ))
Фурье-преобразования для решения задачи
При использовании формулы для оценки расстояния между изображениями при сдвиге (i,j) относительно друг друга
m(X,Y) (i,j) = <X,Y>(i,j) / ( |X|(i,j) ) * |Y|(i,j) ),
получаем, что
- <X,Y> = XxY’ = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- |X|^2 = <X,X> = XxX’xE’ = BFT ( FFT(X) * CONJUGATE ( FFT(X) ) * CONJUGATE ( FFT(E) ) ) = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
- |Y|^2 = <Y,Y> = YxY’xE’ = BFT ( FFT(Y) * CONJUGATE ( FFT(Y) ) * CONJUGATE ( FFT(E) ) )
Где
- <X,Y>(i,j) – скалярное произведение двух изображений, получаемых при сдвиге (i,j) относительно друг друга изображений X и Y
- E – изображение размера равному минимальным размерам X и Y, и заполненное единичными значениями (то есть “кадр” в котором сравниваются X и Y)
- |X|(i,j) – норма общей части изображения X при сдвиге (i,j)
- |Y|(i,j) – норма общей части изображения Y при сдвиге (i,j)
- FFT – операция прямого двухмерного дискретного преобразования Фурье
- BFT – операция обратного двухмерного дискретного преобразования Фурье
- CONJUGATE – операция вычисления матрицы из сопряжённых элементов
- SQUAREMAGNITUDE– операция вычисления матрицы квадратов амплитуд элементов
Упрощение формул для решения поставленной задачи
При решении задачи для поиска одного образца, дополнительное нормирование образца является излишним, а также вычисление нормы у общей части может быть заменено на сумму яркостей пикселей в этой общей части или на сумму квадратов яркостей в этой общей части
При использовании формулы для оценки расстояния между изображениями при сдвиге (i,j) относительно друг друга
m(X,Y) (i,j) = <X,Y>(i,j) / |X|^2(i,j),
получаем, что
- <X,Y> = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- <X,X> = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
Где
- <X,Y>(i,j) – скалярное произведение двух изображений, получаемых при сдвиге (i,j) относительно друг друга изображений X и Y
- E – изображение размера равному минимальным размерам X и Y, и заполненное единичными значениями (то есть “кадр” в котором сравниваются X и Y)
- <X,X>(i,j) – норма (сумма яркостей пикселей) общей части изображения X при сдвиге (i,j)
- FFT – операция прямого двухмерного дискретного преобразования Фурье
- BFT – операция обратного двухмерного дискретного преобразования Фурье
- CONJUGATE – операция вычисления матрицы из сопряжённых элементов
- SQUAREMAGNITUDE– операция вычисления матрицы квадратов амплитуд элементов
Алгоритм поиска фрагмента в полном изображении
- Пусть даны два изображения X и Y – изображение и образец, размеров (N1,N2) и (M1,M2) соответственно и Ni > Mi
- Требуется найти координаты образца Y в полном изображении X и вычислить оценочную величину — меру близости.
- Расширить изображение Y до размера (N1,N2), дополнив его нулями
- Сформировать изображение E из единиц размера (M1,M2) и расширить до размера (N1,N2), дополнив его нулями
- Вычислить <X,Y> = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- Вычислить <X,X> = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
- Вычислить M[i,j] = (f + <X,Y> [i,j])/(f + <X,X> [i,j])
- В матрице M найти элемент с максимальным значением – координаты этого элемента и являются искомой позицией образца в полном изображении, а значение равно оценке меры сравнения.
Примечание:
При использовании дискретного преобразования Фурье, матрица M содержит также элементы от циклического сдвига изображений между собой. Поэтому, если не требуется анализировать циклический сдвиг кадров, то поиск максимального элемента в матрице M нужно ограничить областью (0,0)-(N1-M1, N2-M2).
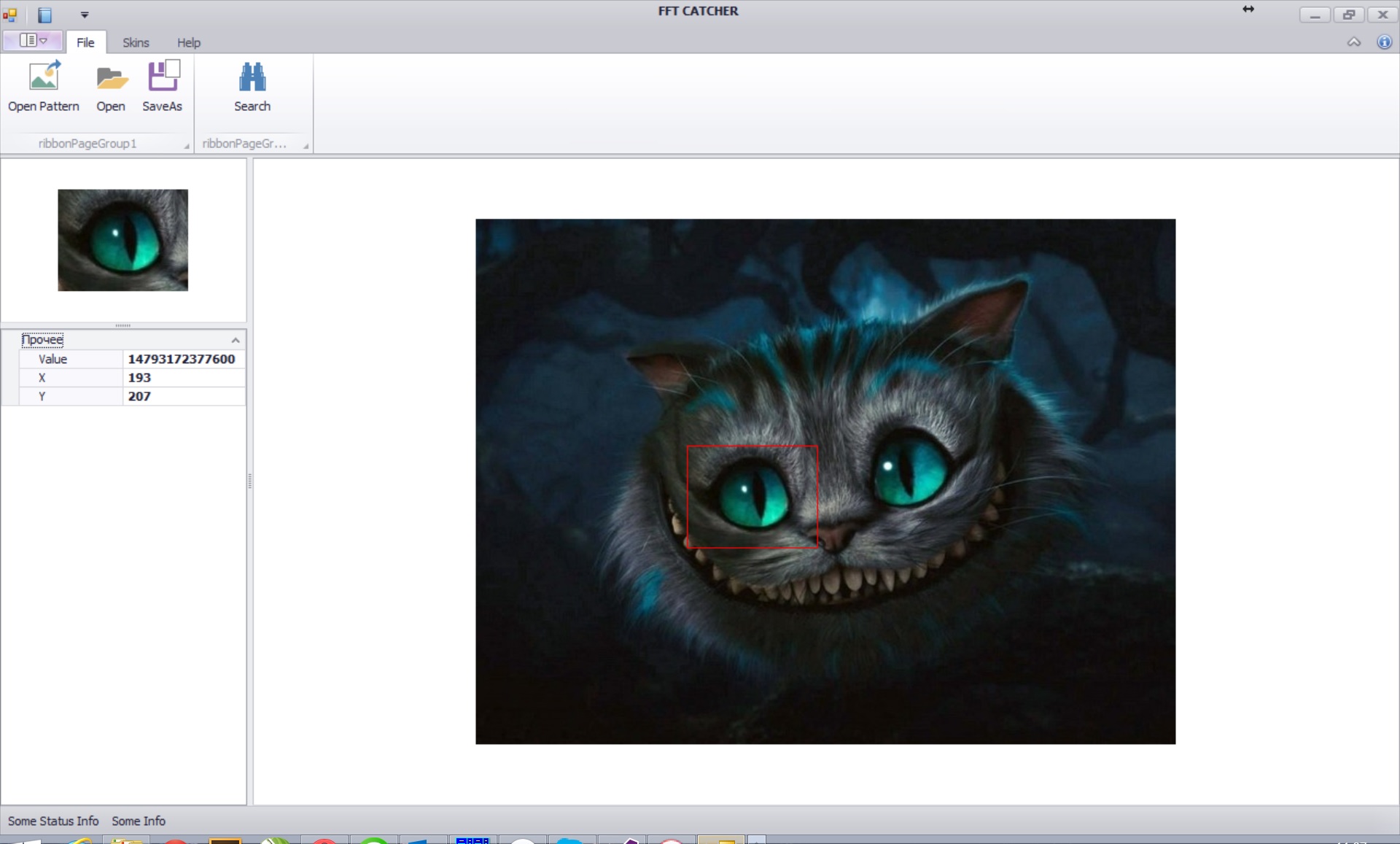
Примеры реализации
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Используемое программное обеспечение
- Microsoft Visual Studio 2013 C# — среда и язык программирования
- EmguCV/OpenCV – C++ библиотека структур и алгоритмов для обработки изображений
- FFTWSharp/FFTW – C++ библиотека реализующая алгоритмы быстрого дискретного преобразования Фурье
/// <summary>
/// Catch pattern bitmap with the Fastest Fourier Transform
/// </summary>
/// <returns>Matrix of values</returns>
private Matrix<double> Catch(Image<Gray, double> image)
{
const double f = 1.0;
int length = image.Data.Length;
int n0 = image.Data.GetLength(0);
int n1 = image.Data.GetLength(1);
int n2 = image.Data.GetLength(2);
Debug.Assert(n2 == 1);
// Allocate FFTW structures
var input = new fftw_complexarray(length);
var output = new fftw_complexarray(length);
fftw_plan forward = fftw_plan.dft_3d(n0, n1, n2, input, output,
fftw_direction.Forward,
fftw_flags.Estimate);
fftw_plan backward = fftw_plan.dft_3d(n0, n1, n2, input, output,
fftw_direction.Backward,
fftw_flags.Estimate);
var matrix = new Matrix<double>(n0, n1);
double[,,] patternData = _patternImage.Data;
double[,,] imageData = image.Data;
double[,] data = matrix.Data;
var doubles = new double[length];
// Calculate Divisor
Copy(patternData, data);
Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double));
input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray());
forward.Execute();
Complex[] complex = output.GetData_Complex();
Buffer.BlockCopy(imageData, 0, doubles, 0, length*sizeof (double));
input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray());
forward.Execute();
input.SetData(output.GetData_Complex().Zip(complex, (x, y) => x*Complex.Conjugate(y)).ToArray());
backward.Execute();
IEnumerable<double> doubles1 = output.GetData_Complex().Select(x => x.Magnitude);
if (_fastMode)
{
// Fast Result
Buffer.BlockCopy(doubles1.ToArray(), 0, data, 0, length*sizeof (double));
return matrix;
}
// Calculate Divider (aka Power)
input.SetData(doubles.Select(x => new Complex(x*x, 0)).ToArray());
forward.Execute();
complex = output.GetData_Complex();
CopyAndReplace(_patternImage.Data, data);
Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double));
input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray());
forward.Execute();
input.SetData(complex.Zip(output.GetData_Complex(), (x, y) => x*Complex.Conjugate(y)).ToArray());
backward.Execute();
IEnumerable<double> doubles2 = output.GetData_Complex().Select(x => x.Magnitude);
// Result
Buffer.BlockCopy(doubles1.Zip(doubles2, (x, y) => (f + x*x)/(f + y)).ToArray(), 0, data, 0,
length*sizeof (double));
return matrix;
}
/// <summary>
/// Copy 3D array to 2D array (sizes can be different)
/// Flip copied data
/// Reduce last dimension
/// </summary>
/// <param name="input">Input array</param>
/// <param name="output">Output array</param>
private static void Copy(double[,,] input, double[,] output)
{
int n0 = output.GetLength(0);
int n1 = output.GetLength(1);
int m0 = Math.Min(n0, input.GetLength(0));
int m1 = Math.Min(n1, input.GetLength(1));
int m2 = input.GetLength(2);
for (int i = 0; i < m0; i++)
for (int j = 0; j < m1; j++)
output[i, j] = input[i, j, 0];
for (int k = 1; k < m2; k++)
for (int i = 0; i < m0; i++)
for (int j = 0; j < m1; j++)
output[i, j] += input[i, j, k];
}
/// <summary>
/// Copy 3D array to 2D array (sizes can be different)
/// Replace items copied by value
/// Flip copied data
/// Reduce last dimension
/// </summary>
/// <param name="input">Input array</param>
/// <param name="output">Output array</param>
/// <param name="value">Value to replace copied data</param>
private static void CopyAndReplace(double[,,] input, double[,] output, double value = 1.0)
{
int n0 = output.GetLength(0);
int n1 = output.GetLength(1);
int m0 = Math.Min(n0, input.GetLength(0));
int m1 = Math.Min(n1, input.GetLength(1));
int m2 = input.GetLength(2);
for (int i = 0; i < m0; i++)
for (int j = 0; j < m1; j++)
output[i, j] = value;
}
/// <summary>
/// Find a maximum element in the matrix
/// </summary>
/// <param name="matrix">Matrix of values</param>
/// <param name="x">Index of maximum element</param>
/// <param name="y">Index of maximum element</param>
/// <param name="value">Value of maximum element</param>
public void Max(Matrix<double> matrix, out int x, out int y, out double value)
{
double[,] data = matrix.Data;
int n0 = data.GetLength(0);
int n1 = data.GetLength(1);
value = data[0, 0];
x = y = 0;
for (int i = 0; i < n0; i++)
{
for (int j = 0; j < n1; j++)
{
if (data[i, j] < value) continue;
value = data[i, j];
x = j;
y = i;
}
}
}
/// <summary>
/// Catch pattern bitmap with the Fastest Fourier Transform
/// </summary>
/// <returns>Array of values</returns>
public Matrix<double> Catch(Bitmap bitmap)
{
using (var image = new Image<Gray, Byte>(bitmap))
return Catch(image);
}
Попался, который кусался
Литература
- А.Л. Дмитриев. Оптические методы обработки информации. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.: Мир 1970
Комментарии (47)

dprotopopov
04.09.2015 20:18-1Два алгоритма состыковать в один, для отсутствия лишних действий, ведь несложная задача?

ZlodeiBaal
04.09.2015 23:52Зачем городить такую колбасину? В чём преимущество перед двумя десятками существующих методов, использующихся для этой же задачки? Многие из таких методов, кстати, значительно стабильнее к искажениям, в том числе к аффинным преобразованиям.

dprotopopov
05.09.2015 00:28-1Зачем городить такую колбасину?
Ответ — Количество требуемых вычислительных операций
Подсчитате оценку сложности — будете ли Вы удовлетворены быстродействием имеющейся у Вас техники?
Если надо один раз и на суперсовременном компе — то это статья не для вас.
ZlodeiBaal
05.09.2015 00:41+3Я пишу алгоритмы в том числе для DSP-процессоров и для embeded процессоров, где производительность это ограниченный ресурс. Я не понимаю как ваш алгоритм хоть как-то превосходит классические алгоритмы поиска. Вы правда считаете, что кто-то сравнивает так: «классический метод “начального уровня”, заключающийся в переборе всех координат».

dprotopopov
05.09.2015 00:48Подсчитате оценку сложности Вашей задачи.
Если обрабатываете очень маленькие картинки — то эта вся методика вам вообще не нужна
Для справки — трудоёмкость дискретного преобразования Фурье быстрыми алгоритмами O(N*logN)

dprotopopov
05.09.2015 01:03В приведённом алгоритме суммарная трудоёмкость будет иметь оценку равную оценке трудоёмкости одного фурье-преобразования, то есть O(N*logN)
Оценим классическую схему с попарным сравнением — это O(N*M^2)
То есть если у Вас образец всегда маленькая картинка — то даже от увеличения общего размера Вы будете наблюдать просто линейный рост трудоёмкости пропорциональный количеству пикселей.
Однако если размер образца тоже возрастает и скорость увеличения больше чем SQRT( LOG ( N ) ) то начиная с некоторого размера изображения этот алгоритм будет работать быстрее, как бы Вы не оптимизировали свой программный код в погоне за белым кроликом.
dprotopopov
05.09.2015 01:15И смею Вас заверить, что на практике это N наступает довольно быстро — если библиотека быстрых преобразований написана грамотно — то уже на картинках в 100-200 пикселей. Если библиотека быстрых преобразований написана тяп-ляп на скриптовом языке — то на 1000-2000 пикселей

ZlodeiBaal
05.09.2015 01:53Почему вы так упёрлись в попарное сравнение? Неужели не знаете других алгоритмов? Да ладно, даже оно. Пирамидальный поиск? Разреженный поиск? Сегментация предварительной области для поиска через цветность/яркость? Это ускоряет его в сотни и тысячи раз. А если затачивать под конкретные задачи, то ещё больше.
Более того, почему вы упёрлись в размер картинки? Я на raspberry Pi обрабатывал мегапиксельные кадры для поиска интересных объектов. При этом объектов не имеющих стабильную форму.
Для справки, поиск примитива на интегральном изображении O(N). Не зря Хаар на нём сделан. И большая часть алгоритмов хэширования изображений. Поиск через FFT и любой локальный классификартор значительно стабильнее и тоже ~N (хотя там достаточно большой коэффициент пропорциональности).

dprotopopov
05.09.2015 02:04-1Почему вы так упёрлись в попарное сравнение? Неужели не знаете других алгоритмов? Да ладно, даже оно. Пирамидальный поиск? Разреженный поиск? Сегментация предварительной области для поиска через цветность/яркость? Это ускоряет его в сотни и тысячи раз. А если затачивать под конкретные задачи, то ещё больше.
Ответ — в основе всего что Вы перечислили всё равно будет лежать некий базовый алгоритм и чаше всего в разных пакетах это попарное сравнение.
Вам никто не мешает и этот алгоритм модифицировать
Например, методом ветвей и границ или каким умеет способом:
сперва сжать изображение и ограничить зону поиска выбором из полученной матрицы оценок несколько наибольших значений.
затем повторить алгоритм но уже только в более достоверных регионах
и как Вы правильно выразились — это ускоряет его в сотни и тысячи раз. (но не миллионы)
повторю ещё раз — на практике эффективность метода можно наблюдать уже на довольно небольших размерах изображений.
dprotopopov
05.09.2015 02:19-2Кстати для предварительной оценки не только формулы из статьи можно использовать — кроме фурье преобразований существует и масса других не менее интересных преобразований — но видимо, сейчас это не входит в программу обучения.

dprotopopov
05.09.2015 02:25и здесь описан алгоритм для задачи один-к-одному
можете сами модифицировать для задачи многие-ко-многим
оптом — дешевле

dprotopopov
05.09.2015 02:38-3Разрешите и Вам задать вопрос по программам и алгоритмам.
Какая из сортировок выполняется на компьютере быстрее?
Варианты:
А. Пузырьковая сортировка
Б. Быстрая сортировка
Совет.
Прежде чем ответить однозначно, подумайте ещё раз.

ZlodeiBaal
05.09.2015 02:48Угу. И строить фурье-преобразование с маской на изображении, по разреженной выборке и пиромидальное так же просто и быстро, как определённого размера блока. Ну-ну. У вас там доступ в память занимает больше времени чем само сравнение.
К тому же вы так же продолжаете игнорировать методы, пропорциональные N, которые решают задачи поиска даже для огромных изображений при большом количестве шумов и искажений.
Впрочем, видя, как вы нервничаете от моих комментариев, отвечая тремя-пятью на каждый, я предпочту откланяться. Конструктивной беседы нет, ни с одним адекватным методом поиска сравнения не приведено.
dprotopopov
05.09.2015 03:14-4Жаль.
Хоть Вы и не смогла дать ответ на вопрос какая из сортировок работает на компьютере быстрее, поскольку не понимаете разницы между терминами алгоритм и программа.
Я хочу посоветовать изучить эту тему на примере другого проекта, посвящённого сравнению времени вычислений на CUDA и MPI некоторых алгоритмов сортировок
github.com/dprotopopov/ParallelSorting
К тому же вы так же продолжаете игнорировать методы, пропорциональные N
А вы опишите их по шагам для той же самой задачи.
Вместе рассчитаем количество элементарных операций.
Я добавлю те же ускорители которые у Вас будут в описании, а может и не буду добавлять.
И мы посчитаем количество элементарных операций.
сравним два этих значения и Вы сами решите — надо ли Вам пользоваться этим алгоритмом или нет.
колхоз — дело добровольное
dprotopopov
05.09.2015 03:30-1Есть и метод с оценкой O(1) — называется «пальцем в небо»
Алгоритм:
Пусть даны два изображения X и Y – изображение и образец, размеров (N1,N2) и (M1,M2) соответственно и Ni > Mi
Требуется найти координаты образца Y в полном изображении X и вычислить оценочную величину — меру близости.
1. Тыкаем в случайную точку на изображеении Y и берём первое число пришедшее в голову
Полученный результат будем рассматривать как решение задачи

dprotopopov
05.09.2015 04:03-1И ещё замечание по поводу DSP-процессоров и для embeded процессоров
Видимо Вы занимаетесь написанием софта для телескопов.
Всякое уменьшение количества операций при анализе изображений без увеличения суммарной ошибки первой и второго рода невозможно если на анализируемое изображение не наложены предоговоренные ограничения.
Если Вы пишете софт для анализа картинок звёздного неба, и при этом пользуетесь софтом который проводит операции сравнения за число шагов равное размеру картинки, то это однозначно указывает, что у Вас уже существует набор предопределённых условий и Ваш софт просто будет отбрасывать всё что не входит в Ваше представление о вселенной.
Вывод.
На Ваших телескопах никогда не будет совершено ни одного открытия — поскольку они будут показывать только то что и та всем известно.
dprotopopov
05.09.2015 04:23-1Видимо Вы занимаетесь написанием софта для телескопов
если Ваш софт отвечает только за ориентацию телескопа — то можно обсуждать.
если Вас софт предназначен для исследования вселенной — я бы Вам рекомендовал вообще забыть что существуют какие-либо программные пакеты компьютерного зрения, а так же описанная мною методика.
dprotopopov
05.09.2015 04:51-1по разреженной выборке
Если же вы производите анализ звёздного неба, то мне вообще непонятно зачем Вам растровые изображения.
Запишите координаты светлых пикселей в таблицу, а дальше просто крутите данными.
Надеюсь, тему расчёт параметров распределений по наблюдаемым данным Вы всё же проходили, теорию вероятностей, статистические критерии и тд?
По любому — если графическое изображение являет собой практически полное чёрное поле, не фиксируемое сенсорами телескопа, то как ни крути — явные вычисления формул по таблицам будет быстрее и надёжнее чем расчёты на каких-то сетках с ячейками поддерживающими точность в пару бит.
Конечно придётся посидеть с карандашом и бумагой, чтобы выписать формулы.
dprotopopov
05.09.2015 05:14-1по разреженной выборке
а у Вас по математике вопроса не возникло — не будет в приведённом алгоритме одни деления на ноль на Ваших данных?
ответ — да, на Ваших данных, практически везде будет деление на ноль.
А почему?
Ответ — а потому, что в данном алгоритме в качестве меры близости выбрана формула соответствующая типовой модели фотографии — где снимки квадратов малевича не делают. То есть отброшены маловероятные варианты из рассмотрения.
А можно по-другому?
Да — можно. Надо изменить предполагаемую модель исходных изображений.
Я расстроен уровнем научных степеней.
dprotopopov
05.09.2015 07:33-1Я расстроен уровнем научных степеней.
Я делал лабы за студентов МФТИ по расчёту задач с краевыми условиями на решетках.
Преподаватель дал такие краевые условия, что получалось что аналитические функции действительного переменного имеют вычет, что может быть только начиная с функций комплексного переменного. Естественно мой результат не совпал с записанным в ответах поскольку расчёты из-за этого противоречия уходили неизвестно куда. Исправилось только после того как я выкинул часть условий из первоначально заданных краевых ограничений.
А ведь другие студенты сдавали так сказать верные решения со всеми этими несоответствиями и получали отличные оценки.
как это возможно — да очень просто — не важно что как считает, главное как отчитаться.

dprotopopov
05.09.2015 03:45-2Посмотрел Ваши публикации — понял Вам практически ничего не рассказывали о теории вероятности — поэтому понятия ошибок первого и второго рода Вы не упоминаете в своих публикациях.
Отсюда у Вас и впечатление. что нет конструктивной беседы, и что метод с оценкой ~N всегда лучше метода с оценкой O(NlogN)

dprotopopov
05.09.2015 02:54-1примитива на интегральном изображении O(N)
так и здесь перемножение элементов двух матриц O(N)
но как говорил кот Матроскин псу Шарику — ты ещё полдня за ним будешь гонятся чтобы фотографию отдать

dprotopopov
05.09.2015 01:36-2в том числе к аффинным преобразованиям
Так здесь этот вопрос не рассматривается.
Никто не спрашивает — никто и не отвечает
а правильно заданный вопрос — это половина ответа

fareloz
05.09.2015 12:40Требуется найти координаты образца Y в полном изображении X и вычислить оценочную величину — меру близости.
То есть в прицнипе кусочек изображения может быть слегка изменен (шум например), и не обязан полностью соотвествовать оригиналу (за исключением масштаба). Я правильно понимаю?
dprotopopov
05.09.2015 13:35-2быть слегка изменен (шум например)
и не только слегка
Вспомните курс математической статистики и теории вероятности
Зная параметры зашумления Вы можете легко рассчитать вероятности ошибок первого и второго рода.
Используется статистический критерий X^2(M) где М-длина образца.
Даже если вы будете точно знать распределение шумов — то всё равно критерий для оценки значительно лучше чем X^2(M) не станет — причина в том что M как правило > 100, а при таком большом числе слагаемых там все с практической точки равносильно сумме нормальных распределений.
Естественно в этой формуле каждое отдельное распределение шума в пикселях образца надо отнормировать на дисперсию.
А можете и не нормировать — тогда просто получите оценку ошибок
dprotopopov
05.09.2015 13:42-1я даже более хочу вам заметить — не существует вещей и явлений известных человеку с характеристикой 100% вероятности.
Кроме Бога

dprotopopov
05.09.2015 14:15-1А X^2(M) при больших M практически совпадает с нормальным распределением.
Естественно надо решить вопросы нормирования.
То есть надо иметь только справочник нормального распределения, чтобы ответить на все вопросы.

dprotopopov
05.09.2015 13:13-1Я правильно понимаю?
Абсолютно верно.
Вспомните операции сравнения векторов в линейном пространстве из школьного курса — там вводится мера на пространстве равная скалярному произведению.
Благодаря нормированию мы тем самым фактически будем искать к заданному вектору-образцу ближайший нормированный вектор из всех возможных таких векторов сформированных из картинки.
Естественно при совпадении направлений двух векторов скалярное произведение будет максимальным.
Почему нормировать лучше на квадрат и не на сумму — просто это из-за цветовосприятия человеческого глаза, под который затачивается и фототехника. Это конечно не закон — это просто обычная практика. Просто Вы должны знать характеристики данных которые намерены обрабатывать для более эффективной их обработки.
То есть — можете делить на корень, а можете вообще не делить, если уверены что в среднем все участки имеют одинаковую интенсивность, например если это не фото, а просто случайные равновероятны данные.

dprotopopov
05.09.2015 15:25-1Приведённые программные коды производят поиск без учёта цветности, то есть в монохромном режиме
Чтобы при поиске учитывать и цвет надо использовать трёхмерный массив для образцов и изображения и делать трёхмерные преобразования Фурье
трёхмерные преобразования тоже содержатся практически во всех библиотеках
Считывать значение меры естественно только из нулевой цветовой плоскости полученной матрицы M

dprotopopov
05.09.2015 16:41-1при этом если написать код для прогона поиска в разных размерах образца
многократно гонять фурье преобразования для образца нет никакой необходимости
поскольку масштабирование получается в результате добавления нулевых или удаления строк и столбцов соответствующих высоким частотам в матрице фурье-образа
а лишнее нормирование делать нет необходимости
получаем что первый квадрант матрицы фурье-образа образца зафиксирован на одном месте в начале координат
а остальные квадранты матрицы перемещаются по строкам и столбцам для перемножения с фурье-образом полного изображения с последующим вычислением обратного преобразования
то же самое для фурье-образа единичной матрицы кадра


Biga
А если масштаб не совпадает, то не будет ведь работать?
dprotopopov
Отмаштабируйте. Прочитайте другую мою статью habrahabr.ru/post/265781 раздел Алгоритм масштабирования изображения
dprotopopov
при этом если написать код для прогнать поиск в разных размерах образца
многократно гонять фурье преобразования для образца нет никакой необходимости
поскольку масштабирование получается в результате добавления нулевых или удаления строк и столбцов соответствующих высоким частотам в матрице фурье-образа
а лишнее нормирование делать нет необходимости
получаем что первый квадрант матрицы фурье-образа образца зафиксирована на одном месте в начале координат
а остальные квадранты матрицы перемещаются по строкам и столбцам для перемножения с фурье-образом полного изображения с последующим вычислением обратного преобразования
то же самое для фурье-образа единичной матрицы кадра
dprotopopov
Алгоритм масштабирования изображения
В оптических системах световой поток в фокальной плоскости системы представляет собой Фурье-преобразование исходного изображения. Размер получаемого на выходе оптической системы изображения определяется соотношением фокальных расстояний объектива и окуляра.
Алгоритм:
Пусть X(N1,N2) – массив яркостей пикселей изображения.
VIK52
dprotopopov
Спасибо, поправлю в тексте.
Хотя в том тексте я нарисовал телескопическую систему из двух линз на самом деле линзы вообще не нужны. оптическую систему предоставляет нам само пространство в котором присутствует свет.
VIK52
В каком тексте? Что-то я нигде не нашел этой картинки
dprotopopov
habrahabr.ru/post/265781
VIK52
Я бы еще придрался к фразе:
Особенно в оптике. Световое поле в типичных оптических задачах, как правило, описывается скалярным приближением уравнений Максвелла, а именно — комплексной скалярной функцией координат и времени. Соответственно и фурье должно быть комплексным.dprotopopov
нет — согласно общепринятому определению Преобразование Фурье — это функции вещественной переменной. либо времени, либо частоты.
Вы просто перепутали с возможным комплексным значением этой функции.
описывается скалярным приближением уравнений Максвелла, а именно — комплексной скалярной функцией координат и времени — да, я понимаю — Вы говорите о тензорах и сверкомплексных
deniskreshikhin
Эм, если уж быть точным то преобразование Фурье если и может сопоставлять функции, то только из пространства Шварца.
В общем-то оно связывает групповые алгебры, а не сами функции.
Т.е. это определение из учебника оно верно только для частного случая, если уж говорить о точном определении преобразовании Фурье, то там есть три пути: 1) Разложение по спектру оператора сдвига на многообразии (это комплексные экспоненты в случае R^n), 2) Частный случай преобразования Гельфанда, 3) Как канонический изоморфизм между групповыми алгебрами, на основе двойственности Понтрягина
В вашем случае, как оно записано, сопоставляются обобщённые функции на R.
dprotopopov
Наверно.
Я ведь экономист по образованию.
VIK52
Скорее уж вы перепутали, если пишете под интегралом экспоненту с мнимой единицей в показателе. Собственно, этот интеграл и есть общепринятое определение, и даже если исходная функция вещественна, то ее фурье-образ — комплексный
dprotopopov
Да — вы правы. В реальном мире мнимого не существует. В реальном мире существует только реальное.
VIK52
Нет, не о тензорах. Эта скалярная функция координат и времени описывает, как ведет себя любая из шести компонент векторов электрического или магнитного поля световой волны.
dprotopopov
реальные — масса и длина
комплексные — плоскость которую видим
сверхкомплексные — пространство-время данные в ощущение
октарионы — неведомо
… — неведомо
а более чем… не обнаружено