В первой части:
Во второй части: цвета и шрифты в графиках R.
В третьей части: параметры графов, вершин и ребер.
В этой части: размещения сети.
Размещения сети — это алгоритмы, возвращающие координаты каждой вершины графа.
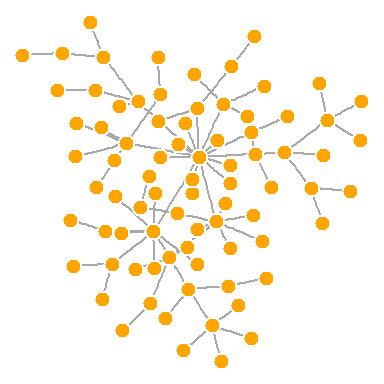
Для исследования размещений создадим немного больший граф, из 80 вершин. Используем функцию barabasi.game, которая генерирует простой граф, начинающийся с одной вершины и наращивающий вершины и ребра в зависимости от заданного уровня предпочтительного присоединения (сколько еще новых объектов предпочтут установить связь с более популярными вершинами в сети).

Можно задать размещение в функции построения:

Или рассчитать координаты вершин заранее:


Это размещение — только пример, оно не слишком полезно. К счастью, в igraph есть набор встроенных размещений, включая такие:



Фрюхтерман-Рейнгольд — один из наиболее часто используемых силовых алгоритмов размещения.
Силовые размещения предполагают создание красивого графа с ребрами одинаковой длины и минимально возможным количеством пересечений. Они представляют граф в виде физической системы. Вершины — электрически заряженные частицы, отталкивающиеся друг от друга при чрезмерном приближении. Ребра ведут себя, как пружины, притягивающие соединенные вершины поближе друг к другу. В результате вершины равномерно распределяются по области графика, а размещение интуитивно в том смысле, что вершины с большим количеством связей находятся ближе друг к другу. Недостаток этих алгоритмов состоит в том, что они довольно медленны, а потому редко используются на графах с количеством вершин больше 1000.
Вот несколько параметров, которые можно задать для этого размещения:
Также можно использовать параметр «веса», который увеличивает силы притяжения между вершинами, связанными более тяжелыми ребрами.
Вы заметите, что размещение не строго определено — разные запуски приводят к немного отличающимся конфигурациям. Сохранение размещения
Размещение

Другой популярный алгоритм силового размещения, показывающий хорошие результаты для связных графов — Камада-Каваи. Как и Фрюхтерман-Рейнгольд, его цель — минимизировать энергию в системе пружин. Igraph также содержит размещение на основе пружин, которое называется

Алгоритм LGL (Large Graph Layout — размещение больших графов) предназначен для больших связных графов. Он также позволяет задать корень — вершину, которая будет располагаться в центре размещения.
По умолчанию координаты графиков масштабируются до интервала [-1,1] как по х, так и по у. Это можно изменить с помощью параметра

По умолчанию igraph использует размещение
Давайте посмотрим на размещения, доступные в igraph:

- визуализация сетей: зачем? каким образом?
- параметры визуализации
- best practices — эстетика и производительность
- форматы данных и подготовка
- описание наборов данных, которые используются в примерах
- начало работы с igraph
Во второй части: цвета и шрифты в графиках R.
В третьей части: параметры графов, вершин и ребер.
В этой части: размещения сети.
Размещения сети
Размещения сети — это алгоритмы, возвращающие координаты каждой вершины графа.
Для исследования размещений создадим немного больший граф, из 80 вершин. Используем функцию barabasi.game, которая генерирует простой граф, начинающийся с одной вершины и наращивающий вершины и ребра в зависимости от заданного уровня предпочтительного присоединения (сколько еще новых объектов предпочтут установить связь с более популярными вершинами в сети).
net.bg <- barabasi.game(80)
V(net.bg)$frame.color <- "white"
V(net.bg)$color <- "orange"
V(net.bg)$label <- ""
V(net.bg)$size <- 10
E(net.bg)$arrow.mode <- 0
plot(net.bg)

Можно задать размещение в функции построения:
plot(net.bg, layout=layout.random)

Или рассчитать координаты вершин заранее:
l <- layout.circle(net.bg)
plot(net.bg, layout=l)

l — матрица x- и y-координат (N x 2) для N вершин графа. Их можно легко задать самостоятельно:l <- matrix(c(1:vcount(net.bg), c(1, vcount(net.bg):2)), vcount(net.bg), 2)
plot(net.bg, layout=l)

Это размещение — только пример, оно не слишком полезно. К счастью, в igraph есть набор встроенных размещений, включая такие:
# Случайно расположенные вершины
l <- layout.random(net.bg)
plot(net.bg, layout=l)

# Размещение по кругу
l <- layout.circle(net.bg)
plot(net.bg, layout=l)

# Размещение в виде 3D-сферы
l <- layout.sphere(net.bg)
plot(net.bg, layout=l)

Фрюхтерман-Рейнгольд — один из наиболее часто используемых силовых алгоритмов размещения.
Силовые размещения предполагают создание красивого графа с ребрами одинаковой длины и минимально возможным количеством пересечений. Они представляют граф в виде физической системы. Вершины — электрически заряженные частицы, отталкивающиеся друг от друга при чрезмерном приближении. Ребра ведут себя, как пружины, притягивающие соединенные вершины поближе друг к другу. В результате вершины равномерно распределяются по области графика, а размещение интуитивно в том смысле, что вершины с большим количеством связей находятся ближе друг к другу. Недостаток этих алгоритмов состоит в том, что они довольно медленны, а потому редко используются на графах с количеством вершин больше 1000.
Вот несколько параметров, которые можно задать для этого размещения:
area (по умолчанию — квадрат количества вершин) и repulserad (радиус подавления для отталкивания — area, умноженная на количество вершин). Оба параметра влияют на расположение графика — изменяйте их, пока не останетесь довольны результатом.Также можно использовать параметр «веса», который увеличивает силы притяжения между вершинами, связанными более тяжелыми ребрами.
Вы заметите, что размещение не строго определено — разные запуски приводят к немного отличающимся конфигурациям. Сохранение размещения
l позволяет получать один и тот же результат много раз, что может быть полезным, если нужно построить изменение графа во времени или разные отношения — и нужно оставить вершины на одних и тех же местах в нескольких графиках.Размещение
fruchterman.reingold.grid аналогично fruchterman.reingold, но быстрее.l <- layout.fruchterman.reingold(net.bg, repulserad=vcount(net.bg)^3,
area=vcount(net.bg)^2.4)
par(mfrow=c(1,2), mar=c(0,0,0,0)) # построить два графика - 1 строка, 2 столбца
plot(net.bg, layout=layout.fruchterman.reingold)
plot(net.bg, layout=l)

dev.off() # выключить графику, чтобы очистить конфигурацию.
Другой популярный алгоритм силового размещения, показывающий хорошие результаты для связных графов — Камада-Каваи. Как и Фрюхтерман-Рейнгольд, его цель — минимизировать энергию в системе пружин. Igraph также содержит размещение на основе пружин, которое называется
layout.spring().l <- layout.kamada.kawai(net.bg)
plot(net.bg, layout=l)
l <- layout.spring(net.bg, mass=.5)
plot(net.bg, layout=l)

Алгоритм LGL (Large Graph Layout — размещение больших графов) предназначен для больших связных графов. Он также позволяет задать корень — вершину, которая будет располагаться в центре размещения.
plot(net.bg, layout=layout.lgl)

По умолчанию координаты графиков масштабируются до интервала [-1,1] как по х, так и по у. Это можно изменить с помощью параметра
rescale=FALSE и масштабировать график вручную, умножая координаты на число. Функция layout.norm позволяет нормализовать график по желаемым границам.l <- layout.fruchterman.reingold(net.bg)
l <- layout.norm(l, ymin=-1, ymax=1, xmin=-1, xmax=1)
par(mfrow=c(2,2), mar=c(0,0,0,0))
plot(net.bg, rescale=F, layout=l*0.4)
plot(net.bg, rescale=F, layout=l*0.6)
plot(net.bg, rescale=F, layout=l*0.8)
plot(net.bg, rescale=F, layout=l*1.0)

dev.off()
По умолчанию igraph использует размещение
layout.auto. Он автоматически подбирает необходимый алгоритм размещения на основании свойств графа (размеру и связности).Давайте посмотрим на размещения, доступные в igraph:
layouts <- grep("^layout\\.", ls("package:igraph"), value=TRUE)
# Убрать размещения, не подходящие для нашего графа.
layouts <- layouts[!grepl("bipartite|merge|norm|sugiyama", layouts)]
par(mfrow=c(3,3))
for (layout in layouts) {
print(layout)
l <- do.call(layout, list(net))
plot(net, edge.arrow.mode=0, layout=l, main=layout) }
dev.off()


