При конвертации проекта из плавающей точки в фиксированную точку инженеры должны определить оптимальные типы данных в фиксированной точке. Эти типы данных должны удовлетворять ограничениям встраиваемой аппаратуры, при этом удовлетворяя системным требованиям по точности вычислений. Fixed-Point Designer™ помогает разрабатывать алгоритмы в фиксированной точке и конвертировать алгоритмы из плавающей точки в фиксированную точку, автоматически предлагая типы данных и атрибуты арифметики в фиксированной точке. При этом предоставляется возможность сравнения результатов симуляции в фиксированной точке с точностью до бита с эталонными результатами в плавающей точке.
В этой статье приводятся оптимальные приемы подготовки кода MATLAB® для конвертации, непосредственной конвертации кода MATLAB в фиксированную точку и оптимизации алгоритмов для эффективности и производительности. Если вы разрабатываете алгоритмы в фиксированной точке в MATLAB для последующего ручного написания кода или конвертируете в фиксированную точку для автоматической генерации кода, то описанные приемы помогут вам превратить ваш код MATLAB общего назначения в эффективный код в фиксированной точке.
Подготовка кода к переводу в фиксированную точку
Есть три шага, которые следует предпринять для обеспечения плавного процесса конвертации:
Отделение основного алгоритма от остального кода MATLAB
Обычно алгоритм сопровождается кодом, который подготавливает входные данные и кодом, который создает графики для верификации результатов. Поскольку в фиксированную точку нужно сконвертировать только ядро алгоритма, более эффективно будет структурировать код таким образом, чтобы отдельный тестовый файл создавал входы, вызывал основной алгоритм и строил графики результатов. При этом основной алгоритм также будет находиться в отдельном файле или файлах (Таблица 1).
Таблица 1. Код до и после отделения основного алгоритма от тестовой обвязки.
Подготовка алгоритмического кода к инструментированию и ускорению
Инструментирование и ускорение позволяют упростить процесс конвертации. Fixed-Point Designer используется для инструментирования кода и записи минимальных и максимальных значений всех именованных и промежуточных переменных. Этот инструмент может использовать записанные значения, чтобы предложить типы данных для использования в коде в фиксированной точке.
С использованием Fixed-Point Designer можно также ускорять алгоритмы в фиксированной точке путем создания MEX файла, и ускорять симуляции, требуемые для верификации реализации в фиксированной точке относительно оригинальной версии.
Инструментирование и ускорение полагаются на технологию генерации кода, поэтому прежде чем их использовать, требуется подготовить алгоритм к генерации кода – даже если вы не планируете использовать MATLAB Coder™ или HDL Coder™ для генерации кода C или кода HDL.
Вначале требуется определить функции или конструкции в вашем коде MATLAB, не поддерживаемые для генерации кода (см. Поддержка языка для получения списка поддерживаемых функций и объектов).
Есть два способа для автоматизации этого шага:
После подготовки алгоритма к генерации кода, можно использовать Fixed-Point Designer для инструментирования и ускорения кода. Используйте
Проверка поддержки фиксированной точки функциями, используемыми в алгоритмическом коде
При выявлении функции, не поддерживаемой для генерации кода, у вас есть три возможности:
Затем можно продолжить конвертацию кода в фиксированную точку, и вернуться к неподдерживаемой функции, когда у вас будет подходящая замена (Таблица 2).
Таблица 2. Код до и после изоляции операции в плавающей точке при помощи приведения типа (обратное приведение типа к фиксированной точке на выходе не показано).
Управление типами данных и ограничение роста разрядности
В реализации с фиксированной точкой переменные в фиксированной точке должны оставаться в арифметике с ограниченной разрядностью, и не должны произвольно превращаться в плавающую точку. Также важно предотвратить рост разрядности.
Например, рассмотрим следующий код:
Это выражение перезаписывает y значением
Для сохранения типа данных y используйте синтаксис
Таблица 3. Код до и после использования индексного присваивания для предотвращения роста разрядности.
Создание таблицы с типами для разделения определений типов данных и алгоритмического кода
Разделение определений типов данных и алгоритмического кода упрощает сравнение реализаций в фиксированной точке и перенос алгоритма на другое целевое оборудование.
Для применения этой лучшей практики надо сделать следующее:
Таблица 4a. Код до и после создания таблицы типов данных для отделения алгоритмического кода от определений типов.
Таблица 4б. Код до и после добавления типа данных единичной точности к таблице типов.
Добавление типов данных в фиксированной точке в таблицу типов
После создания таблицы с определениями типов данных, вы можете добавить типы данных в фиксированной точке на основании ваших целей конвертации в фиксированную точку. Например, если вы планируете реализовать алгоритм на языке C, размер слова типов данных в фиксированной точке будет ограничен числами, кратными 16. С другой стороны, если вы планируете реализовывать в HDL, размер слова не ограничен.
Чтобы получить набор предложенных типов данных для вашего кода, используйте команды Fixed-Point Designer
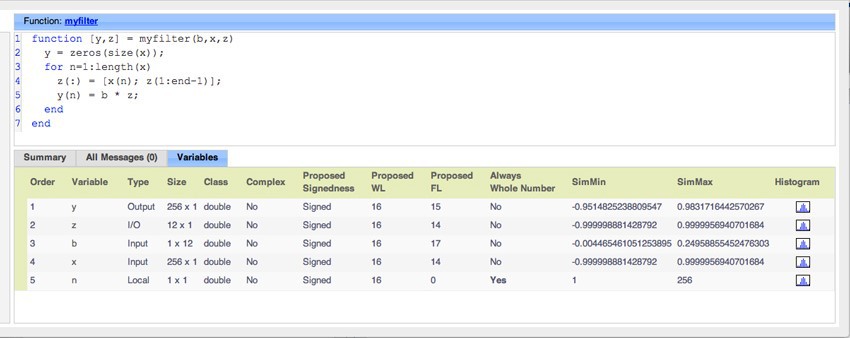
Рисунок 1. Отчет по генерации кода, созданный showInstrumentationResults с предложенными типами данных для переменных в алгоритме фильтрации.
Затем вы можете подстроить предложенные типы при необходимости (Таблицы 5 и 6).
Таблица 5. Алгоритм фильтрации и тестовый скрипт для инструментирования и выполнения кода и отображения предложенных типов данных в фиксированной точке для переменных.
Таблица 6. Тестовый скрипт и алгоритм фильтрации из Таблицы 4 с типами данных в фиксированной точке.
Запустите ваш алгоритм с новыми типами данных в фиксированной точке и сравните выход с результатами эталонного алгоритма в плавающей точке.
Оптимизация типов данных
Выбрали ли вы ваши собственные типы в фиксированной точке или использовали предложенные Fixed-Point Designer, всегда ищите возможности по оптимизации размеров слова, размеров дробной части, знаковости и, возможно, даже режимов арифметики (fimath). Это можно сделать с использованием разрядных чисел двойной точности (scaled doubles), рассматривая гистограмму значений переменной или путем тестирования различных типов данных из вашей таблицы типов.
Использование Scaled Doubles для выявления потенциальных переполнений
Scaled doubles являются гибридами чисел в плавающей точке и фиксированной точке. Fixed-Point Designer хранит scaled doubles в виде чисел двойной точности, но сохраняет информацию о разрядности, знаке и длине слова. Для использования scaled doubles требуется установить свойство перезаписи типа данных (data type override, DTO) (Таблица 7).
Таблица 7. Методы установки свойства перезаписи типов данных – локально и глобально.
Не забудьте сбросить глобальный DTO, если в нем больше нет необходимости, при помощи команды
Используйте buildInstrumentedMex для запуска вашего кода и showInstrumentationResults для просмотра результатов. В отчете по генерации кода значения, которые бы переполнились, подсвечены красным цветом (Рисунок 2).
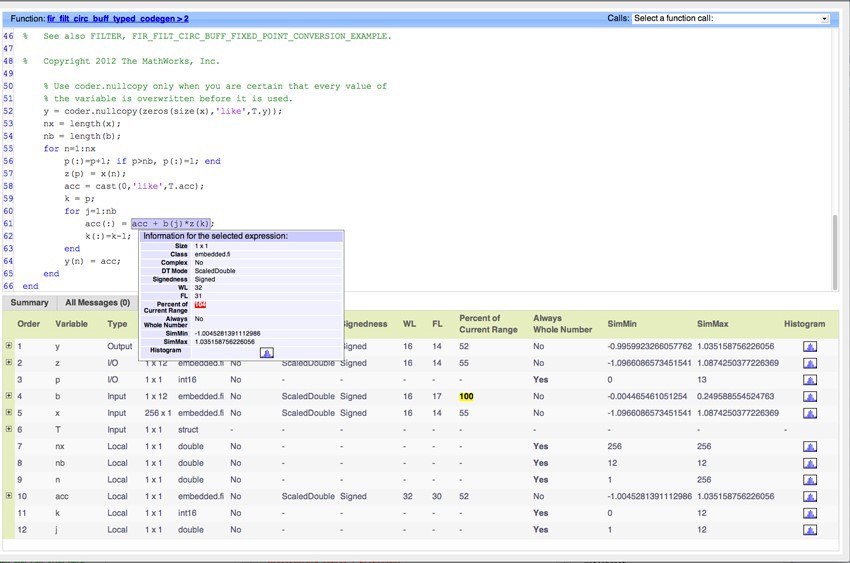
Рисунок 2. Отчет по генерации кода, показывающий переполнения при использовании типа Scaled Doubles (слева) и иконка гистограммы (справа).
Проверка распределения значений переменной
Вы можете использовать гистограмму для выявления типов данных со значениями, которые находятся в допустимом диапазоне, вне диапазона или ниже разрешения (точности). Щелкнув по иконке гистограммы, можно запустить NumericTypeScope и увидеть распределение значений, наблюдаемых во время симуляции для выбранной переменной (Рисунок 3).
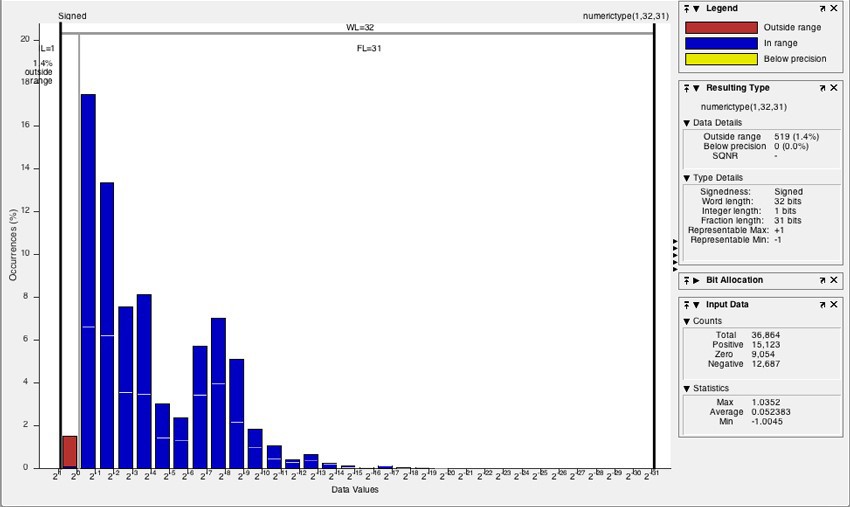
Рисунок 3. Гистограмма, показывающая распределение значений переменной, которая переполнилась (“Outside range”), показанное красным цветом.
Тестирование различных типов данных из таблицы типов
Вы можете добавлять собственные вариации типов данных в фиксированной точке в таблицу типов (Таблица 8).
Таблица 8. Тестовый скрипт для изучения эффектов использования различных типов данных в фиксированной точке из таблицы типов для функции фильтрации.
Сравнение результатов разных итераций для верификации точности алгоритма после каждого изменения (Рисунок 4).
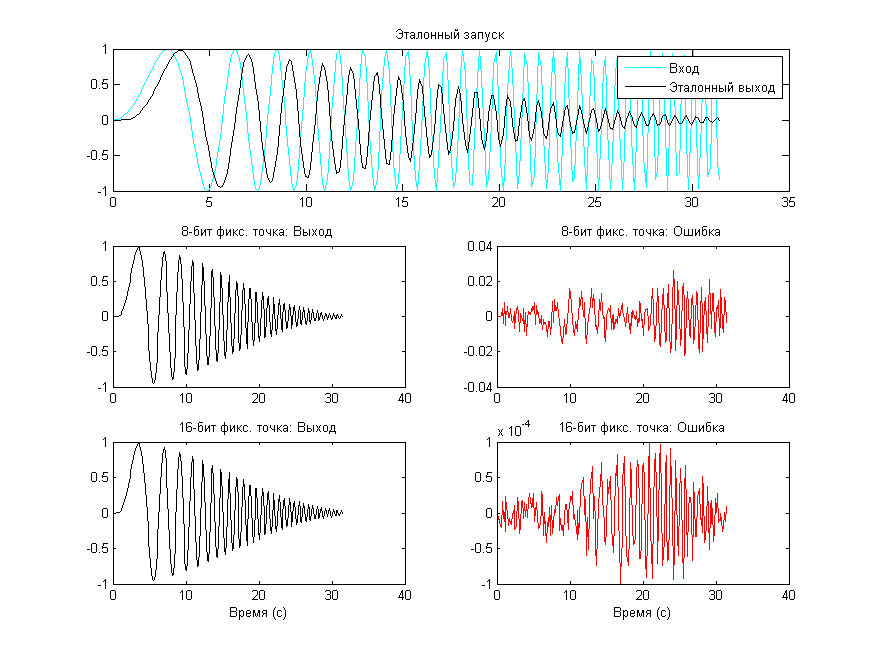
Рисунок 4. Графики результатов тестового скрипта из Таблицы 8, показывающие выход и ошибку после конвертации в 8-битные и 16-битные типы данных в фиксированной точке.
Оптимизация алгоритма
Существуют три наиболее распространенных способа оптимизации вашего алгоритма для улучшения производительности и генерации более эффективного кода C.
Вы можете:
Использование свойств fimath для улучшения эффективности сгенерированного кода
При использовании настроек fimath по умолчанию, может генерироваться дополнительный код для реализации насыщения при переполнении, округления и арифметики с полной точностью (Таблица 9а).
Таблица 9а. Оригинальный код MATLAB и код C, сгенерированный с настройками fimath по умолчанию.
Чтобы сгенерированный код был более эффективным, требуется выбрать такие настройки арифметики с фиксированной точкой, которые подходят типам вашего процессора. Используйте свойства fimath для описания арифметики, способов округления и действий при переполнении, чтобы задать правила осуществления арифметических операций с вашими объектами fi (Таблица 9б).
Таблица 9б. Оригинальный код MATLAB и код C, сгенерированный с настройками fimath, подходящими к типам процессора.
Замена встроенных функций реализациями в фиксированной точке
Некоторые функции MATLAB могут быть заменены для получения более эффективной реализации в фиксированной точке. Например, можно заменить встроенную функцию интерполяционной таблицей или реализацией CORDIC, которой требуются только итеративные операции сдвига и суммирования.
Реализация операций деления другими способами
Операции деления часто не поддерживаются полностью со стороны аппаратуры, и могут привести к медленным вычислениями. Когда в вашем алгоритме требуется операция деления, рассмотрите возможность замены её на более быструю альтернативу. Если знаменатель является степенью двойки, используйте битовый сдвиг; например, используйте bitsra(x,3) вместо x/8. Если знаменатель является константой, умножьте на обратную величину; например, используйте x*0.2 вместо x/5.
Что дальше?
После конвертации вашего кода в плавающей точке в фиксированную точку с применением описанных лучших подходов с использованием Fixed-Point Designer, потратьте время на тщательное тестирование реализации в фиксированной точке с использованием реалистичных тестовых входов и сравните результаты симуляции с точностью до бита с вашим эталоном в плавающей точке.
В этой статье приводятся оптимальные приемы подготовки кода MATLAB® для конвертации, непосредственной конвертации кода MATLAB в фиксированную точку и оптимизации алгоритмов для эффективности и производительности. Если вы разрабатываете алгоритмы в фиксированной точке в MATLAB для последующего ручного написания кода или конвертируете в фиксированную точку для автоматической генерации кода, то описанные приемы помогут вам превратить ваш код MATLAB общего назначения в эффективный код в фиксированной точке.
Подготовка кода к переводу в фиксированную точку
Есть три шага, которые следует предпринять для обеспечения плавного процесса конвертации:
- Отделить основной алгоритм от остального кода.
- Подготовить код для инструментирования и ускорения.
- Проверить используемые функции на поддержку фиксированной точки.
Отделение основного алгоритма от остального кода MATLAB
Обычно алгоритм сопровождается кодом, который подготавливает входные данные и кодом, который создает графики для верификации результатов. Поскольку в фиксированную точку нужно сконвертировать только ядро алгоритма, более эффективно будет структурировать код таким образом, чтобы отдельный тестовый файл создавал входы, вызывал основной алгоритм и строил графики результатов. При этом основной алгоритм также будет находиться в отдельном файле или файлах (Таблица 1).
| Оригинальный код | Модифицированный код |
|---|---|
|
Тестовый файл.Файл с алгоритмом. |
Таблица 1. Код до и после отделения основного алгоритма от тестовой обвязки.
Подготовка алгоритмического кода к инструментированию и ускорению
Инструментирование и ускорение позволяют упростить процесс конвертации. Fixed-Point Designer используется для инструментирования кода и записи минимальных и максимальных значений всех именованных и промежуточных переменных. Этот инструмент может использовать записанные значения, чтобы предложить типы данных для использования в коде в фиксированной точке.
С использованием Fixed-Point Designer можно также ускорять алгоритмы в фиксированной точке путем создания MEX файла, и ускорять симуляции, требуемые для верификации реализации в фиксированной точке относительно оригинальной версии.
Инструментирование и ускорение полагаются на технологию генерации кода, поэтому прежде чем их использовать, требуется подготовить алгоритм к генерации кода – даже если вы не планируете использовать MATLAB Coder™ или HDL Coder™ для генерации кода C или кода HDL.
Вначале требуется определить функции или конструкции в вашем коде MATLAB, не поддерживаемые для генерации кода (см. Поддержка языка для получения списка поддерживаемых функций и объектов).
Есть два способа для автоматизации этого шага:
- Добавить директиву
в начале файла MATLAB, содержащего ядро вашего алгоритма. Эта директива сообщает анализатору кода, что следует отмечать функции и конструкции, которые не содержатся в подмножестве языка MATLAB, поддерживаемого для генерации кода.%#codegen - Использовать инструмент проверки готовности кода для создания отчета, который выявляет обращения к функциям и использование типов данных, не поддерживаемых для генерации кода.
После подготовки алгоритма к генерации кода, можно использовать Fixed-Point Designer для инструментирования и ускорения кода. Используйте
buildInstrumentedMexshowInstrumentationResultsfiaccelПроверка поддержки фиксированной точки функциями, используемыми в алгоритмическом коде
При выявлении функции, не поддерживаемой для генерации кода, у вас есть три возможности:
- Заменить функцию на эквивалентную функцию в фиксированной точке.
- Написать собственную эквивалентную функцию.
- Изолировать неподдерживаемую функцию используя приведение типа к double на входе функции, и обратное приведение типа к фиксированной точке на выходе.
Затем можно продолжить конвертацию кода в фиксированную точку, и вернуться к неподдерживаемой функции, когда у вас будет подходящая замена (Таблица 2).
| Оригинальный код | Модифицированный код |
|---|---|
|
|
Управление типами данных и ограничение роста разрядности
В реализации с фиксированной точкой переменные в фиксированной точке должны оставаться в арифметике с ограниченной разрядностью, и не должны произвольно превращаться в плавающую точку. Также важно предотвратить рост разрядности.
Например, рассмотрим следующий код:
y = y + x(n)Это выражение перезаписывает y значением
y + x(n)Для сохранения типа данных y используйте синтаксис
(:) =y(:) = y + x(n)| Оригинальный код | Модифицированный код |
|---|---|
|
|
Создание таблицы с типами для разделения определений типов данных и алгоритмического кода
Разделение определений типов данных и алгоритмического кода упрощает сравнение реализаций в фиксированной точке и перенос алгоритма на другое целевое оборудование.
Для применения этой лучшей практики надо сделать следующее:
- Использовать
илиcast(x,'like',y)
для приведения типа переменной к желаемому типы данных при первом определении переменной.zeros(m,n,'like',y) - Создать таблицу определений типов, начиная с оригинальных типов данных, используемых в коде – обычно, в плавающей точке двойной точности – типа данных по умолчанию в MATLAB (Таблица 4а).
- До конвертации в фиксированную точку, добавить тип данных single в таблицу типов для поиска несоответствий и других проблем (Таблица 4б).
- Осуществить верификацию привязки, запустив код, привязанный к каждой таблице, с различными типами данных и сравнив результаты.
| Оригинальный код | Модифицированный код |
|---|---|
|
|
| Оригинальный код | Модифицированный код |
|---|---|
|
|
Добавление типов данных в фиксированной точке в таблицу типов
После создания таблицы с определениями типов данных, вы можете добавить типы данных в фиксированной точке на основании ваших целей конвертации в фиксированную точку. Например, если вы планируете реализовать алгоритм на языке C, размер слова типов данных в фиксированной точке будет ограничен числами, кратными 16. С другой стороны, если вы планируете реализовывать в HDL, размер слова не ограничен.
Чтобы получить набор предложенных типов данных для вашего кода, используйте команды Fixed-Point Designer
buildInstrumentedMexshowInstrumentationResults
Рисунок 1. Отчет по генерации кода, созданный showInstrumentationResults с предложенными типами данных для переменных в алгоритме фильтрации.
Затем вы можете подстроить предложенные типы при необходимости (Таблицы 5 и 6).
| Код алгоритма | Тестовый файл |
|---|---|
|
|
| Код алгоритма | Тестовый файл | Таблица типов |
|---|---|---|
|
|
|
Запустите ваш алгоритм с новыми типами данных в фиксированной точке и сравните выход с результатами эталонного алгоритма в плавающей точке.
Оптимизация типов данных
Выбрали ли вы ваши собственные типы в фиксированной точке или использовали предложенные Fixed-Point Designer, всегда ищите возможности по оптимизации размеров слова, размеров дробной части, знаковости и, возможно, даже режимов арифметики (fimath). Это можно сделать с использованием разрядных чисел двойной точности (scaled doubles), рассматривая гистограмму значений переменной или путем тестирования различных типов данных из вашей таблицы типов.
Использование Scaled Doubles для выявления потенциальных переполнений
Scaled doubles являются гибридами чисел в плавающей точке и фиксированной точке. Fixed-Point Designer хранит scaled doubles в виде чисел двойной точности, но сохраняет информацию о разрядности, знаке и длине слова. Для использования scaled doubles требуется установить свойство перезаписи типа данных (data type override, DTO) (Таблица 7).
| Установка DTO | Пример |
|---|---|
DTO установлен локально используя |
|
DTO установлен глобально используя |
|
Не забудьте сбросить глобальный DTO, если в нем больше нет необходимости, при помощи команды
reset(fipref)Используйте buildInstrumentedMex для запуска вашего кода и showInstrumentationResults для просмотра результатов. В отчете по генерации кода значения, которые бы переполнились, подсвечены красным цветом (Рисунок 2).

Рисунок 2. Отчет по генерации кода, показывающий переполнения при использовании типа Scaled Doubles (слева) и иконка гистограммы (справа).
Проверка распределения значений переменной
Вы можете использовать гистограмму для выявления типов данных со значениями, которые находятся в допустимом диапазоне, вне диапазона или ниже разрешения (точности). Щелкнув по иконке гистограммы, можно запустить NumericTypeScope и увидеть распределение значений, наблюдаемых во время симуляции для выбранной переменной (Рисунок 3).

Рисунок 3. Гистограмма, показывающая распределение значений переменной, которая переполнилась (“Outside range”), показанное красным цветом.
Тестирование различных типов данных из таблицы типов
Вы можете добавлять собственные вариации типов данных в фиксированной точке в таблицу типов (Таблица 8).
| Код алгоритма | Тестовый файл | Таблица типов |
|---|---|---|
|
|
|
Сравнение результатов разных итераций для верификации точности алгоритма после каждого изменения (Рисунок 4).

Рисунок 4. Графики результатов тестового скрипта из Таблицы 8, показывающие выход и ошибку после конвертации в 8-битные и 16-битные типы данных в фиксированной точке.
Оптимизация алгоритма
Существуют три наиболее распространенных способа оптимизации вашего алгоритма для улучшения производительности и генерации более эффективного кода C.
Вы можете:
- Использовать свойства fimath для улучшения эффективности сгенерированного кода
- Заменять встроенные функции более эффективными реализациями в фиксированной точке
- Реализовывать операции деления иными методами
Использование свойств fimath для улучшения эффективности сгенерированного кода
При использовании настроек fimath по умолчанию, может генерироваться дополнительный код для реализации насыщения при переполнении, округления и арифметики с полной точностью (Таблица 9а).
| Код MATLAB | Сгенерированный код C |
|---|---|
|
|
Чтобы сгенерированный код был более эффективным, требуется выбрать такие настройки арифметики с фиксированной точкой, которые подходят типам вашего процессора. Используйте свойства fimath для описания арифметики, способов округления и действий при переполнении, чтобы задать правила осуществления арифметических операций с вашими объектами fi (Таблица 9б).
| Код MATLAB | Сгенерированный код C |
|---|---|
|
|
Замена встроенных функций реализациями в фиксированной точке
Некоторые функции MATLAB могут быть заменены для получения более эффективной реализации в фиксированной точке. Например, можно заменить встроенную функцию интерполяционной таблицей или реализацией CORDIC, которой требуются только итеративные операции сдвига и суммирования.
Реализация операций деления другими способами
Операции деления часто не поддерживаются полностью со стороны аппаратуры, и могут привести к медленным вычислениями. Когда в вашем алгоритме требуется операция деления, рассмотрите возможность замены её на более быструю альтернативу. Если знаменатель является степенью двойки, используйте битовый сдвиг; например, используйте bitsra(x,3) вместо x/8. Если знаменатель является константой, умножьте на обратную величину; например, используйте x*0.2 вместо x/5.
Что дальше?
После конвертации вашего кода в плавающей точке в фиксированную точку с применением описанных лучших подходов с использованием Fixed-Point Designer, потратьте время на тщательное тестирование реализации в фиксированной точке с использованием реалистичных тестовых входов и сравните результаты симуляции с точностью до бита с вашим эталоном в плавающей точке.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

