Линейная алгебра в Data Science и Machine Learning является основополагающей. Новички, начинающие свой путь обучения в области Data Science, а также признанные практики должны развить хорошее понимание основных понятий линейной алгебры.

Специально к новому старту курса математика и Machine Learning для Data Science делимся переводом статьи Бенджамина Оби Тайо — физика, кандидата наук и преподавателя Data Science — о том, что нужно знать, чтобы лучше понимать Data Science и Machine Learning.

Линейная алгебра — это раздел математики, который чрезвычайно полезен в Data Science и машинном обучении. Владение линейной алгеброй — это также самый важный математический навык в машинном обучении. Большинство моделей машинного обучения могут быть выражены в матричном виде. Сам набор данных часто представляется в виде матрицы. Линейная алгебра используется при предварительной обработке данных, в преобразовании данных и оценке моделей. Вот темы, с которыми вы должны быть знакомы:

• Векторы.

• Матрицы.

• Транспонирование матрицы.

• Обратная матрица.

• Определитель матрицы.

• След матрицы.

• Скалярное произведение.

• Собственные значения.

• Собственные векторы.

В этой статье мы проиллюстрируем применение линейной алгебры в Data Science и Machine Learning с использованием набора данных рынка технологических акций, который можно найти здесь.

Линейная алгебра для предварительной обработки данных

Мы начнём с иллюстрации того, как линейная алгебра применяется для предварительной обработки данных.

Импорт необходимых библиотек линейной алгебры

import numpy as np
import pandas as pd
import pylab
import matplotlib.pyplot as plt
import seaborn as sns

Чтение набора данных и отображение признаков

data = pd.read_csv("tech-stocks-04-2021.csv")
data.head()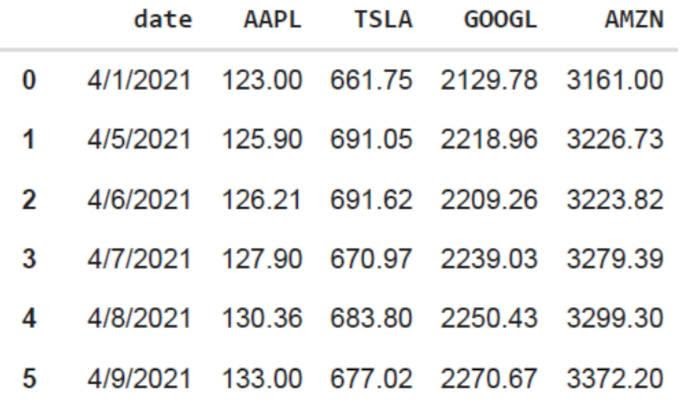

print(data.shape)
output = (11,5) 

Функция data.shape позволяет нам узнать размерность нашего набора данных. В этом случае набор данных содержит 5 признаков (date, AAPL, TSLA, GOOGL и AMZN) и каждый содержит 11 наблюдений. Дата (date) относится к торговым дням в апреле 2021 года (до 16 апреля). AAPL, TSLA, GOOGL и AMZN — это цены закрытия акций Apple, Tesla, Google и Amazon соответственно.

Визуализация данных

Чтобы выполнить визуализацию данных, нужно определить столбцовые матрицы визуализируемых признаков:

x = data['date']
y = data['TSLA']
plt.plot(x,y)
plt.xticks(np.array([0,4,9]), ['Apr 1','Apr 8','Apr 15'])
plt.title('Tesla stock price (in dollars) for April 2021',size=14)
plt.show()

Ковариационная матрица

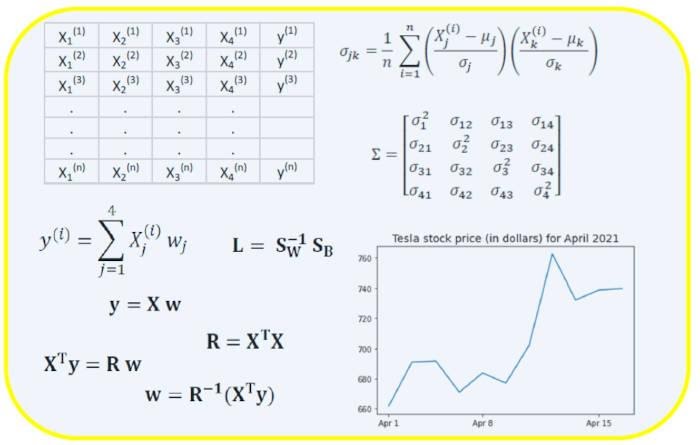
Ковариационная матрица является одной из наиболее важных матриц в Data Science и Machine Learning. Она предоставляет информацию о совместном движении (корреляции) между признаками. Предположим, у нас есть матрица признаков с 4 признаками и n наблюдениями, как показано в таблице 2:

Чтобы визуализировать корреляции между признаками, мы можем сгенерировать диаграмму рассеяния:

cols=data.columns[1:5]
print(cols)
output = Index(['AAPL', 'TSLA', 'GOOGL', 'AMZN'], dtype='object')
sns.pairplot(data[cols], height=3.0)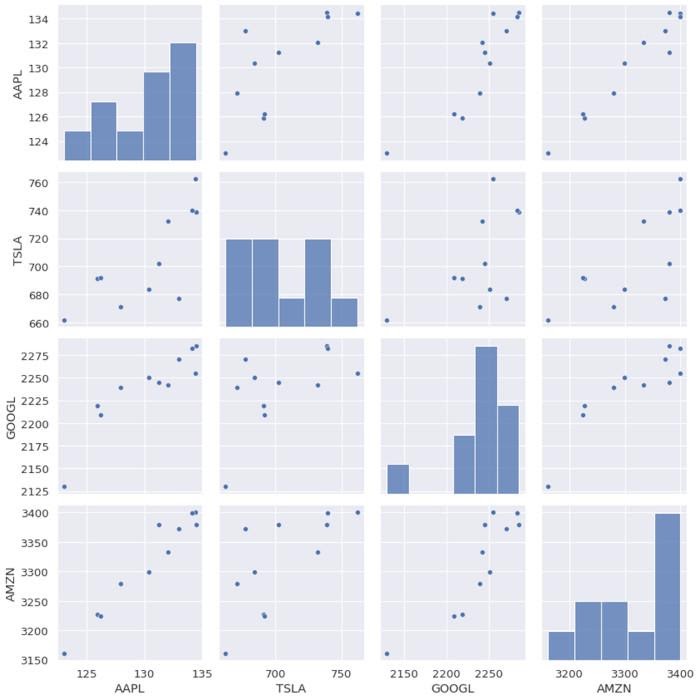

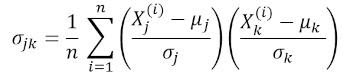
где ? и ? — среднее значение и стандартное отклонения признака соответственно. Это уравнение указывает, что при нормализации признаков матрица ковариации представляет собой просто точечное произведение между признаками. Ковариационная матрица может быть выражена в виде вещественной и симметричной матрицы 4 х 4:

Эта матрица может быть преобразована в диагональную путём выполнения унитарного преобразования, также называемого преобразованием анализа главных компонентов (PCA), чтобы получить следующее:

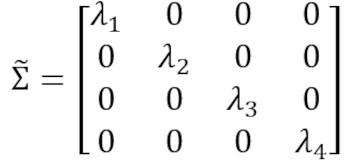
Поскольку след матрицы при унитарном преобразовании остаётся инвариантным, мы наблюдаем, что сумма собственных значений диагональной матрицы равна общей дисперсии, содержащейся в признаках X₁, X₂, X₃ и X₄.

Вычисление ковариационной матрицы для технологических акций

from sklearn.preprocessing import StandardScaler
stdsc = StandardScaler()
X_std = stdsc.fit_transform(data[cols].iloc[:,range(0,4)].values)
cov_mat = np.cov(X_std.T, bias= True)

Обратите внимание, что при этом используется транспонирование нормализованной матрицы.

Визуализация ковариационной матрицы

plt.figure(figsize=(8,8))
sns.set(font_scale=1.2)
hm = sns.heatmap(cov_mat,
                 cbar=True,
                 annot=True,
                 square=True,
                 fmt='.2f',
                 annot_kws={'size': 12},
                 yticklabels=cols,
                 xticklabels=cols)
plt.title('Covariance matrix showing correlation coefficients')
plt.tight_layout()
plt.show()

Из рисунка 3 видно, что AAPL сильно коррелирует с GOOGL и AMZN и слабо с TSLA. TSLA обычно слабо коррелирует с AAPL, GOOGL и AMZN, в то время как AAPL, GOOGL и AMZN сильно коррелируют друг с другом.

Вычисление собственных значений ковариационной матрицы

np.linalg.eigvals(cov_mat)
output = array([3.41582227, 0.4527295 , 0.02045092, 0.11099732])
np.sum(np.linalg.eigvals(cov_mat))
output = 4.000000000000006
np.trace(cov_mat)
output = 4.000000000000001 

Мы наблюдаем, что, как и ожидалось, след ковариационной матрицы равен сумме собственных значений.

Вычисление кумулятивной дисперсии

Поскольку след матрицы остаётся инвариантным при унитарном преобразовании, мы наблюдаем, что сумма собственных значений диагональной матрицы равна общей дисперсии, содержащейся в признаках X₁, X₂, X₃ и X₄. Следовательно, мы можем определить следующие величины:

Обратите внимание, что когда p = 4, кумулятивная дисперсия, как и ожидалось, становится равной 1.

eigen = np.linalg.eigvals(cov_mat)
cum_var = eigen/np.sum(eigen)
print(cum_var)
output = [0.85395557 0.11318237 0.00511273 0.02774933]

print(np.sum(cum_var))
output = 1.0

Из кумулятивной дисперсии (cum_var) мы видим, что 85 % дисперсии содержатся в первом собственном значении и 11 % — во втором. Это означает, что при реализации PCA могут использоваться только первые два основных компонента, поскольку 97 % общей дисперсии приходятся на эти 2 компонента. Это может существенно уменьшить размерность пространства признаков (с 4 до 2), когда реализован PCA.

Матрица линейной регрессии

Предположим, у нас есть набор данных, который имеет 4 признака предиктора и n наблюдений, как показано ниже.

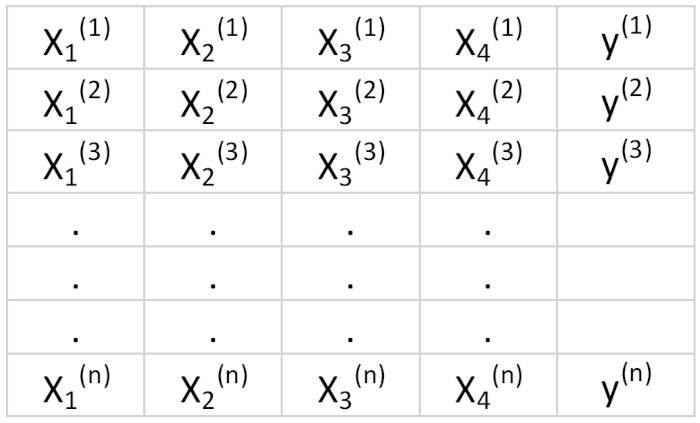
Мы хотели бы построить модель множественной регрессии для прогнозирования значений y (столбец 5). Таким образом, наша модель может быть выражена так:

.

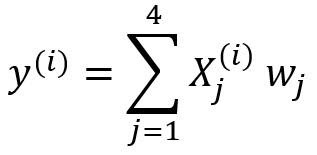
В матричном виде это уравнение можно записать так:

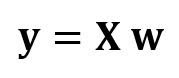
где X — матрица признаков (n x 4), w — матрица (4 x 1), представляющая определяемые коэффициенты регрессии, и y — матрица (n x 1), содержащая n наблюдений целевой переменной y.

Обратите внимание, что X является прямоугольной матрицей, поэтому мы не можем решить приведённое выше уравнение, взяв обратную X величину.

Чтобы преобразовать X в квадратную матрицу, мы умножаем левую и правую части нашего уравнения на транспонирование из X, то есть:

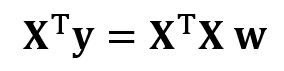
Это уравнение можно записать так:

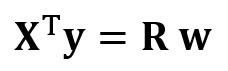
Где

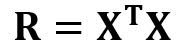
является матрицей регрессии (4?4). Мы наблюдаем, что R — это вещественная и симметричная матрица. Обратите внимание, что в линейной алгебре транспонирование произведения двух матриц подчиняется следующему соотношению:

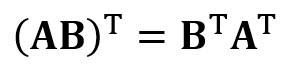
Теперь, когда мы сократили нашу задачу регрессии и выразили её в терминах (4?4) вещественной, симметричной и обратимой матрицы регрессии R, легко показать, что точное решение уравнения регрессии выглядит так:

.

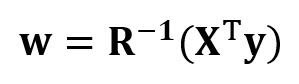
Примеры регрессионного анализа для прогнозирования непрерывных и дискретных переменных приведены ниже:

• Основы линейной регрессии для абсолютных новичков.

• Построение перцептронного классификатора с помощью метода наименьших квадратов.

Матрица линейного дискриминантного анализа

Другим примером реальной и симметричной матрицы в Data Science является матрица линейного дискриминантного анализа (LDA). Эта матрица может быть выражена так:

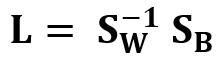
Где S_W — матрица рассеяния в пределах признака (the within-feature scatter matrix), а S_B — матрица рассеяния между признаками. Поскольку обе матрицы S_W и S_B вещественны и симметричны, из этого следует, что L также вещественна и симметрична. Диагонализация L создаёт подпространство признаков, которое оптимизирует раздельность классов и уменьшает размерность. Следовательно, LDA является алгоритмом обучения с учителем, а PCA — нет.

Чтобы узнать больше о реализации LDA, пожалуйста, ознакомьтесь со следующими ссылками:

• Машинное обучение: уменьшение размерности с помощью линейного дискриминантного анализа.

• Репозиторий GitHub для реализации LDA с использованием набора данных Iris.

• Машинное обучение Python от Себастьяна Рашки, 3-е изд. (глава 5).

Резюме

Итак, мы обсудили несколько применений линейной алгебры в Data Science и машинном обучении. Используя набор данных рынка технологических акций, мы проиллюстрировали важные понятия, такие как размер матрицы, столбцовые матрицы, квадратные матрицы, ковариационные матрицы, транспонирование матрицы, собственные значения, точечные произведения и т. д. 

Линейная алгебра является важным инструментом в Data Science и машинном обучении. Таким образом, новички, интересующиеся Data Science, должны ознакомиться с основными понятиями линейной алгебры.

Чтобы в деталях разобраться с внутренней механикой Data Science, не оставив без внимания машинное обучение, вы можете присмотреться к нашему курсу математика и Machine Learning для Data Science, где опытные менторы и эксперты в своём деле ответят на сложные вопросы, устранят неясности и правильно направят ваши размышления, чтобы в дальнейшем вы решали сложные проблемы самостоятельно.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering