Большинство статей про алгоритмы, используемые для решения задачи многорукого бандита, очень академичны. Они пестрят формулами, графиками и статистическими таблицами. При этом как будто подразумевается, что у нас есть неизменяемый набор ручек для дёргания и n>? попыток. В этой статье я постараюсь рассказать об этих алгоритмах с колокольни обычного разработчика, применительно к реальным условиям, в которых работает наш продукт (но графики будут — с ними красивее).

Дисклеймер: эта статья написана обычным разработчиком, не дата-саентистом или аналитиком. Не стоит рассматривать её в качестве серьёзного научного труда и искать неточности, неполноту и крайности. Она не про это.

Так как это статья про конкретное практическое применение, то и термины буду использовать из нашего домена:

• просмотр(n) = попытка;

• смайл(s) = победа;

• смайлрейт(w, от worth) = количество смайлов/количество просмотров;

• контент = то, у чего есть эти самые просмотры и смайлы.

Классическая постановка задачи многорукого бандита в этих терминах, если совсем грубо, звучит так: не зная заранее, насколько хороший контент загружают нам в приложение, необходимо максимизировать итоговый смайлрейт. Но такая постановка задачи хороша только с точки зрения среднестатистического потребителя контента. На практике же всё несколько сложнее.

Есть множество нюансов. Например, есть создатели контента, которым важно внимание (читай: «просмотры»). Есть персонализация, которой для качественной работы необходимо набирать достаточно данных по всему контенту, а не только по самому топовому (пропустить хороший контент из-за того, что ему немного не повезло — это плохо). И так далее.

Ещё немного контекста. В нашем флагманском мобильном приложении iFunny, в одновременной ротации, находится около 40 тысяч единиц контента. При этом постоянно поступает новый, со средней скоростью один мем в две секунды, а старый с той же скоростью из ротации уходит. То есть у нас не статичный набор контента, на котором любой алгоритм в той или иной мере сойдётся и начнёт максимально эффективно решать нашу задачу, а довольно подвижная структура, в которую постоянно добавляется контент (о котором мы ничего не знаем) и удаляются проверенные «курочки Рябы», несущие золотые яйца (то есть смайлы). Отсюда возникают дополнительные моменты, на которые пришлось обратить внимание.

Мы экспериментировали с четырьмя алгоритмами:

• UCB1.

• eGreedy.

• Wilson.

• Thompson Sampling.

Первые три из них упоминаются довольно часто, а четвёртый, по неведомой мне причине, сильно обделён вниманием.

Для наглядности, для каждого алгоритма добавлю анимацию и финальное состояние натурного эксперимента, который проводился по следующей методике:

1. 1000 единиц контента с предопределённым эталонным смайлрейтом, распределённым нормально от 0.0 до 0.006.

2. 10 тыс. пользователей. У каждого пользователя есть история просмотров и повторно один и тот же контент он не получит.

3. 10 итераций, где каждый пользователь по очереди запрашивает 10 единиц контента (суммарно 1 млн просмотров).

4. Вес контента рассчитывается честно. Используется не эталонный смайлрейт, а реальный, зависящий от количества просмотров и смайлов конкретной единицы контента.

5. Смайлы раздаются относительно честно. Когда реальный смайлрейт опускается ниже эталонного — есть 10% вероятность, что очередной пользователь, увидевший этот контент, поставит смайл.

UCB1

Наверное, самый известный алгоритм. Это детерминированный алгоритм — то есть при одинаковых входных данных он будет возвращать один и тот же ответ.

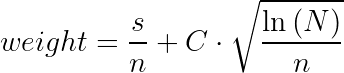
Где:

• s — смайлы;

• n — просмотры;

• С — коэффициент;

• N — суммарное количество просмотров по всему контенту.

Как видно, левая часть определяет «доходность» конкретного контента, а правая ответственна за эксплорацию (даёт шанс проявить себя контенту с малым количеством просмотров). Коэффициентом C можно в некоторой степени влиять на баланс между заработком и эксплорацией.

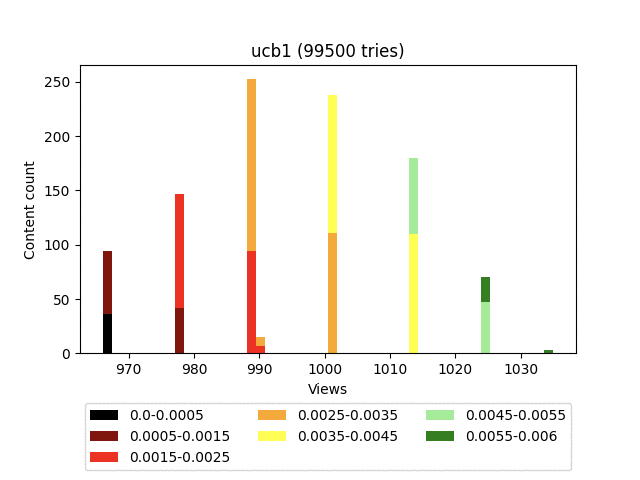
Результат:

Анимация:

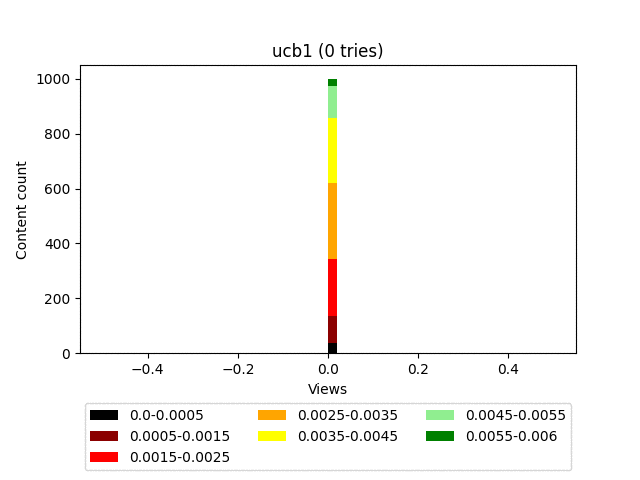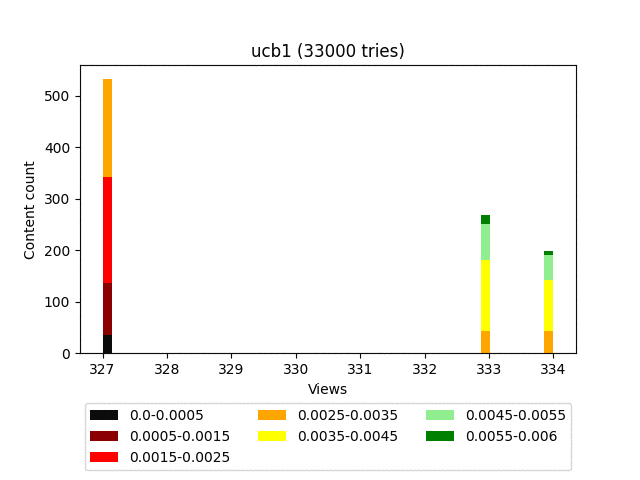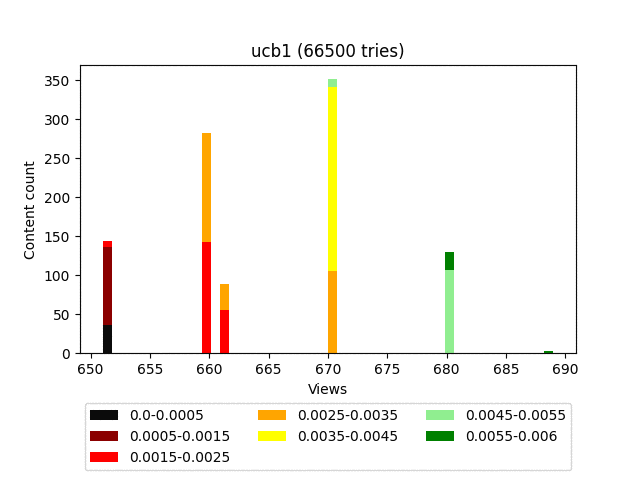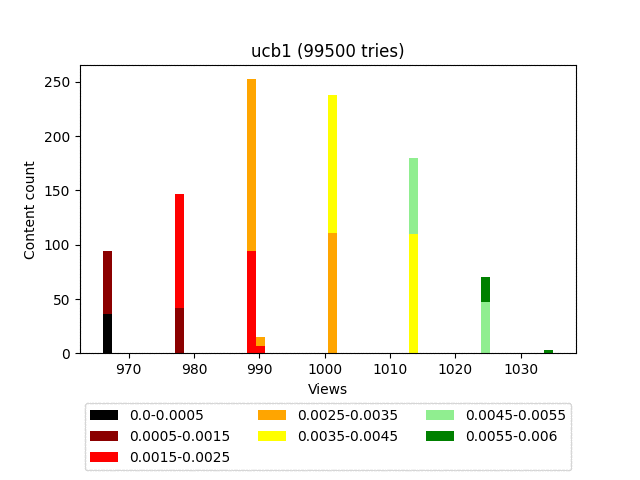
Плюсы:

• Прост в реализации.

• Не требователен к вычислительным ресурсам.

• Вес можно частично рассчитывать на лету, при изменении статистики конкретного контента, что ускоряет выдачу пользователю.

Минусы:

• Самая тяжёлая (относительно) часть расчётов происходит в момент запроса на сортировку, так как завязана на суммарное количество просмотров по всему контенту и на лету пришлось бы пересчитывать вообще всё.

  Лайфхак: при достаточно большом суммарном объёме просмотров можно не заморачиваться вычислением sqrt(ln(N)), а принять его константным. Отклонения если и будут, то настолько мизерные, что никакого реального ущерба точности не принесут. Также можно закешировать значения корней для всех n в разумных пределах. По памяти будет недорого, а скорости даст очень хорошо.

• У этого алгоритма очень сильно слагаемое, ответственное за эксплорацию. И, как видно на графике, он в целом тянет наверх весь контент довольно плотной группой.

Таким образом, учитывая постоянную ротацию, старый качественный контент сильно проигрывает новому, с малым количеством показов. Примем N=10000, C=1 и посмотрим, как ведут себя два разных контента.

Контент №1:

• просмотры = 500;

• смайлы = 50;

• вес = 0.1 + 0.14 = 0.24.

Контент №2:

• просмотры = 1000;

• смайлы = 100;

• вес = 0.1 + 0.09 = 0.19.

Казалось бы, сохранение такого смайлрейта на протяжении 1000 показов — вполне себе показатель качества, но порадовать пользователя этим контентом уже практически без шансов.

Давайте посчитаем, каким минимальным смайлрейтом должен обладать контент с 500 просмотрами, чтобы победить заслуженного ветерана:

смайлрейт + SQRT(ln(10000)/500) > 0.19
смайлрейт > 0.05 

Необходимо иметь всего 25 смайлов на 500 просмотров. То есть объективно в два раза хуже, зато свежак.

Тут следует отметить, что в минусы я отнёс этот пункт исключительно из-за того, что для нас фокус оказался смещён слишком сильно. Но при этом надо понимать, что сама суть задачи многорукого бандита в том и состоит, что нужно поддерживать разумный баланс между «заработком» на найденном хорошем контенте и эксплорацией нового.

eGreedy

Алгоритм, лично у меня вызывающий добрую улыбку. Суть проста до безобразия: есть некое пороговое значение (эпсилон), мы кидаем кубик и, если он больше этого значения, то отдаём самый топ, отсортированный по смайлрейту. Если меньше, то включаем эксплорацию — отдаём случайный контент.

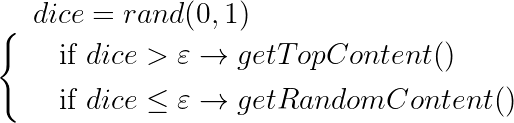
Результат:

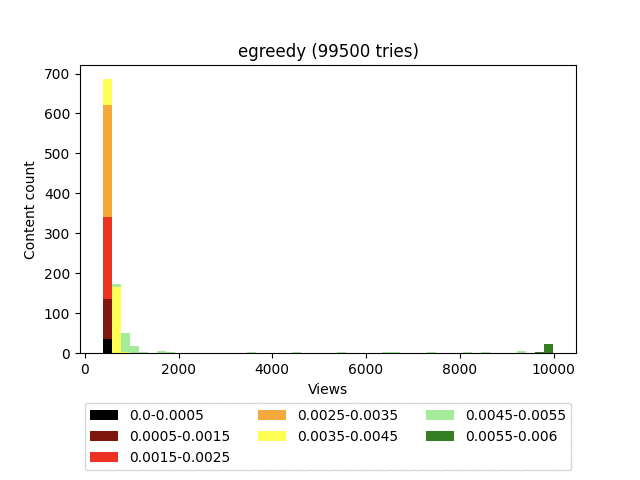
Анимация:

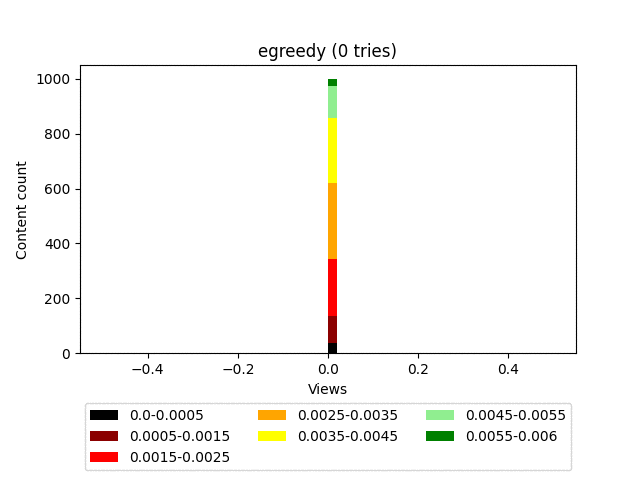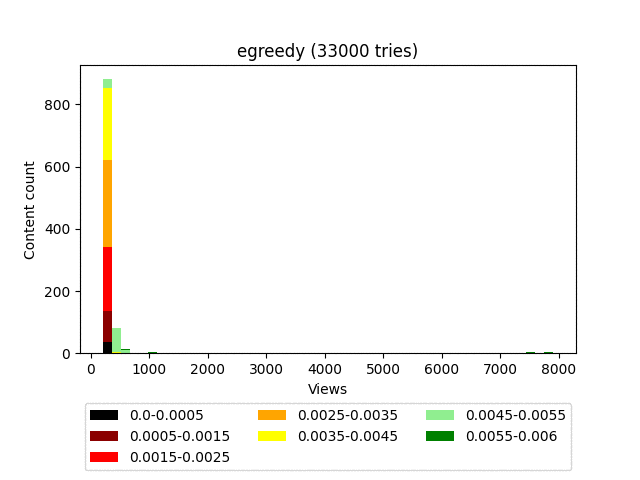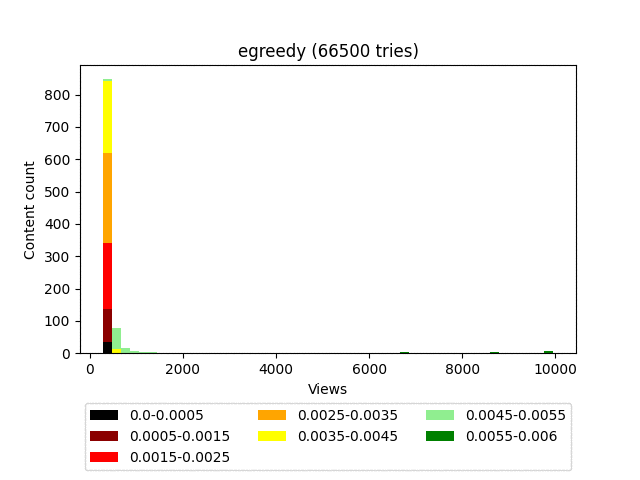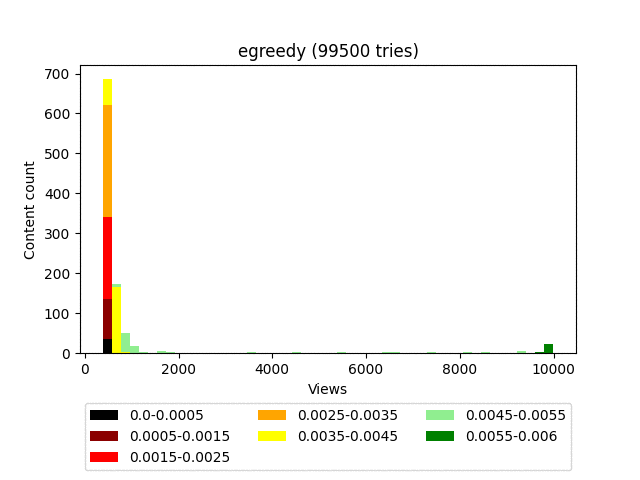
Плюсы:

• Очень прост в реализации.

• Очень дёшев по вычислительным ресурсам.

• Вес рассчитывается на лету при изменении статистики конкретного контента.

• Довольно быстро находит самый ценный контент и запускает его в космос.

Минусы:

• Алгоритм максималист, идеальный горец — остаться должен только один! Будь в тебе хотя бы минимальный изъян — будешь отправлен к аутсайдерам.

• Нет механизмов отсечения однозначно плохого контента.

Алгоритм очень хорошо выводит в топ действительно качественный контент, но при этом не делает никакого разделения на хорошее и плохое внутри гораздо большей когорты контента. Это приводит к очень неровной пользовательской ленте, где самый топовый контент будет в довольно больших количествах перемешиваться с откровенным шлаком, что не очень хорошо влияет на глубину просмотра. 

Так как вес контента считается крайне примитивно, он не пессимизирует контент с большим количеством просмотров и даёт равные шансы как для проверенного 100/1000, так и для выскочки 1/10. Получается ситуация обратная UCB1 — в проигрыше всегда оказывается потенциально хороший контент с меньшим количеством просмотров.

Контент_1=100/1000=0.1
Контент_2=10/100=0.1

А теперь выдадим каждому по одному дополнительному просмотру. Вроде мелочь, но:

Контент_1=100/1001=0.0999
Контент_2=10/101=0.0990

Упс. Из топа выпадаем и вся надежда на рандом. В нашем случае с постоянной ротацией контента — это довольно неприятная особенность.

Wilson

Как и UCB1, является детерминированным алгоритмом.

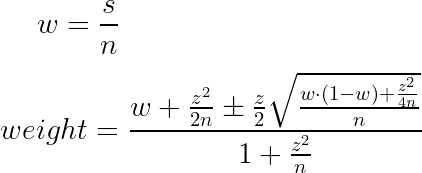
Где:

• w — смайлрейт;

• n — просмотр;

• z — константа, определяющая величину доверительного интервала;

• ± — определяет, по какой границе доверительного интервала будем вычислять вес.

В задаче многорукого бандита используется верхняя граница доверительного интервала. Нижний доверительный интервал, как приятный бонус, можно использовать для получения самого топового топа.

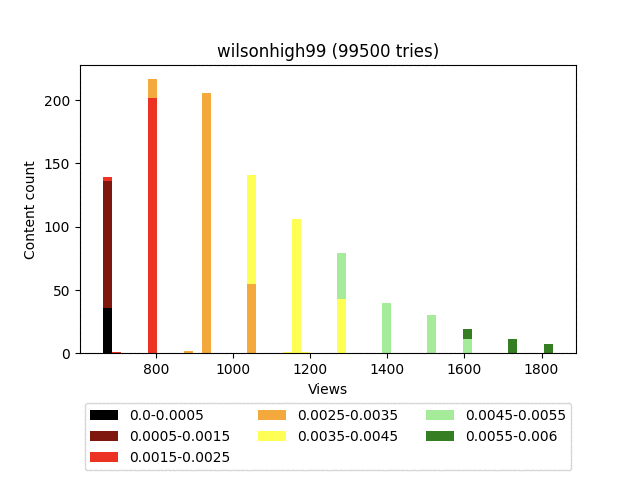
Результат:

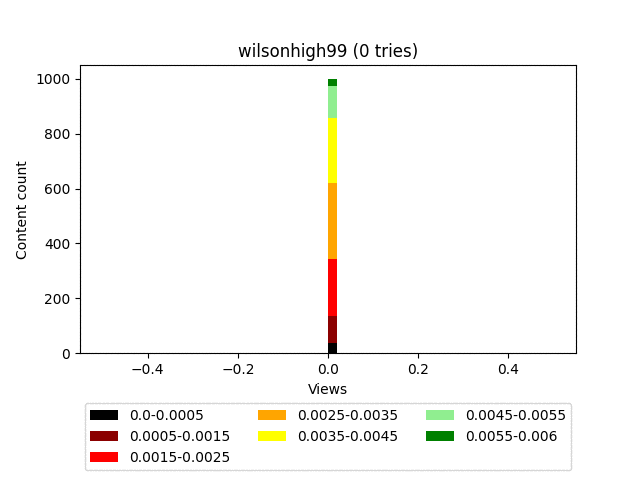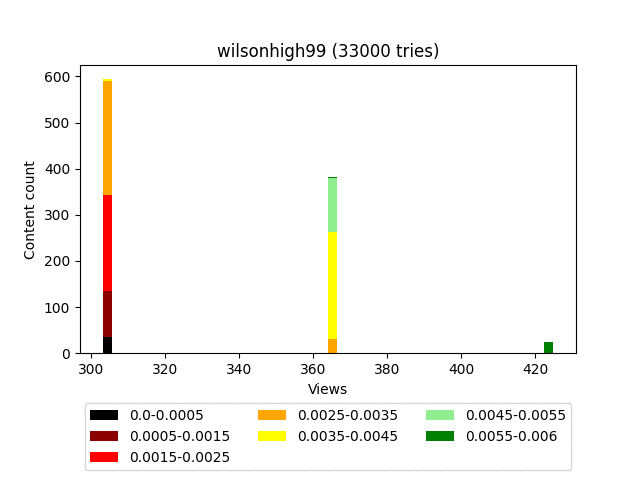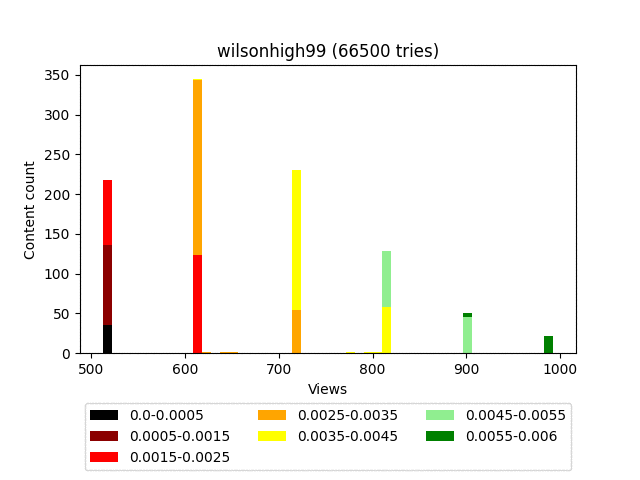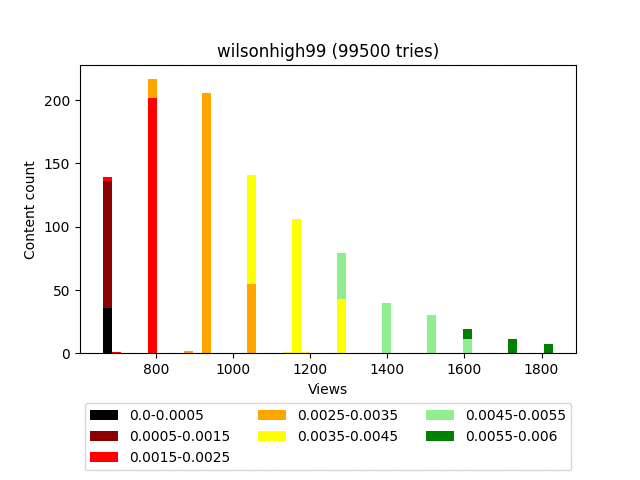
Анимация:

Плюсы:

• Вес полностью рассчитывается на лету, так как завязан только на статистику конкретного контента.
  
  Из этой особенности следует одно неочевидное, но крайне приятное следствие. При выдаче пользователю нам не нужно пробегаться по всему набору и дорасчитывать вес. Вместо этого можно сразу делать выборку greatestN и радоваться жизни. (Кстати, сортировка тоже не нужна - существуют гораздо более экономичные решения для выбора N лучших)

• Даёт хорошее распределение. Качественно пессимизирует гарантированно плохой контент.

Минусы:

• Страшная формула. Этот недостаток можно чуть сгладить, умножив верхнюю и нижнюю часть уравнения на n.

Думаю, вы заметили довольно странное итоговое распределение - забором. Связано это с тем, что он строго детерминированный и завязан исключительно на статистику самого контента. Грубо говоря, на большом количестве итераций, контент, имеющий равное количество смайлов, будет иметь и равное количество просмотров.

В наших конкретных условиях это не плюс и не минус, а просто особенность.

Thompson Sampling

Самый замороченный по математике алгоритм. Если совсем простыми словами, то для каждого контента мы строим бета-распределение и берём его значение в случайной точке.

Формулы приводить не буду, в интернете очень много статей разной степени научности, разбирающих этот алгоритм. А графически это выглядит как-то вот так:

Результат:

Анимация:

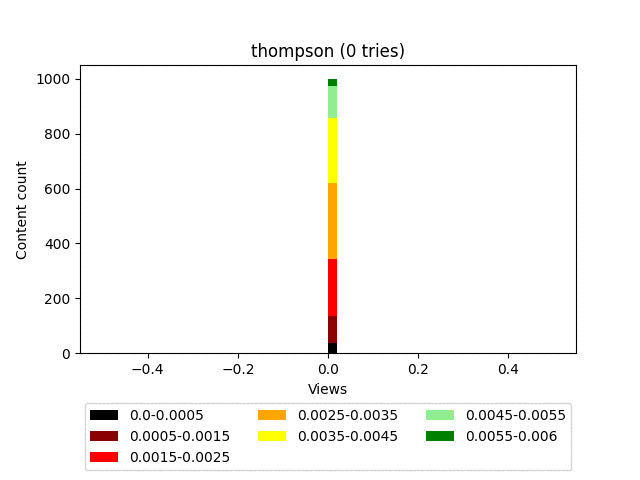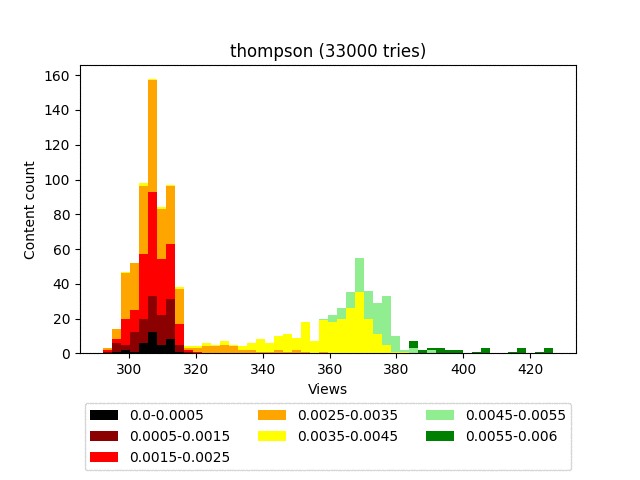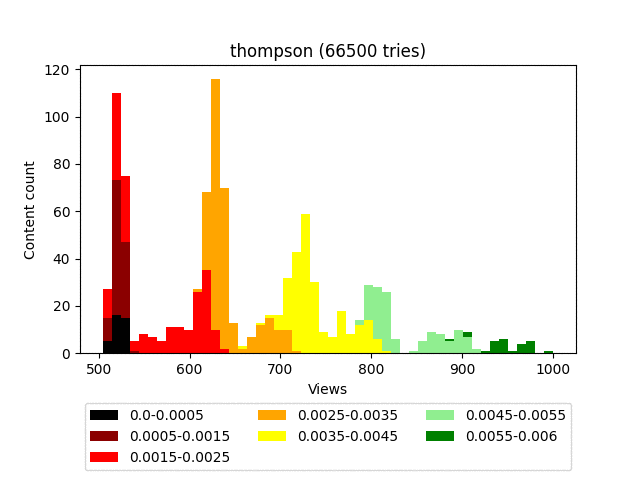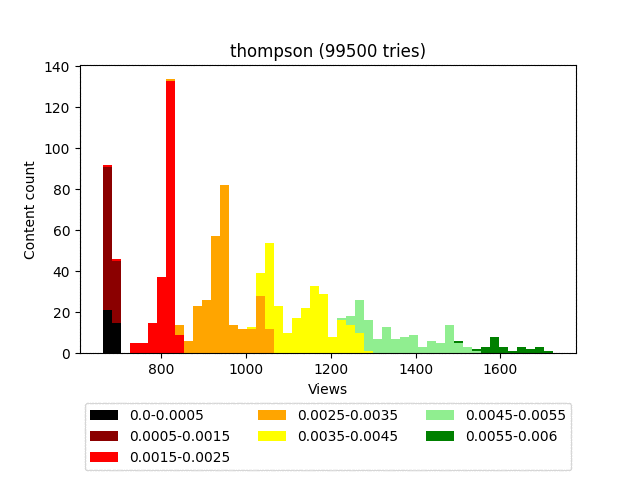
Плюсы:

• Даёт хорошее распределение. Качественно пессимизирует гарантированно плохой контент.

• Чертовски красив в графическом представлении.

Минусы:

• Очень тяжёлый по вычислительным ресурсам.

• Сложный в реализации. И нет нормальных библиотек под Java.

• Алгоритм отлит в бетоне и не предполагает из коробки каких-либо настроек, влияющих на эксплорацию.

• Из-за рандома вес необходимо считать в момент сортировки.

Лайфхак: частично сложность можно нивелировать, заранее рассчитав бета-распределения для всех разумных значений пар smile/view.

Ещё лайфхак: можно закешировать значения сэмплов для всех этих пар с шагом, например, 0.01. Тогда он начинает работать довольно быстро, но ценою точности и потребления памяти. Например, считаем, что разумное количество просмотров лежит в диапазоне 0…5000, а разумное количество смайлов в диапазоне 0…500.

Итого выходит: 5000?500?100(сэмплов)?4(байт во float) = ~1ГБ памяти.

В принципе, жить можно, но такое.

Вместо выводов

Их не будет. Выбор подходящего именно вам алгоритма — долгая и кропотливая работа аналитиков, море гипотез, А/Б-тестов, графиков бизнес-метрик и поиск компромиссов. Задача же разработчика — всё это реализовать так, чтобы оно работало качественно, быстро и, желательно, не требовало постройки нового ЦОД-а. Надеюсь, эта статья кому-нибудь поможет с последними двумя пунктами.